一類混合整數(shù)規(guī)劃模型的共享車調(diào)度優(yōu)化算法研究

馬艷利,陳明秀

(1.寧夏大學新華學院 信息與計算機科學系, 寧夏 銀川 750021; 2.寧夏大學新華學院 工程與應用科學系，寧夏 銀川 750021)

0 引言

隨著我國經(jīng)濟的快速發(fā)展，城市交通問題和擁堵問題日益嚴重.共享車作為一種新型的出行工具，解決了城市“最后一公里”問題.共享車在運行過程中自發(fā)地產(chǎn)生了供需不平衡問題，為了解決這一問題，需要對車輛進行調(diào)度，這個調(diào)度過程被稱為共享車調(diào)度問題(bikesharing rebalance problem，BRP).

現(xiàn)有研究中，共享車調(diào)度大致分為兩類：靜態(tài)共享車調(diào)度(SBRP)和動態(tài)共享車調(diào)度(DBRP).靜態(tài)調(diào)度相關文獻大多都圍繞著再平衡操作而確定車輛路線，將所研究區(qū)域分割成小區(qū)域，用平衡工具進行再平衡操作.不同的文獻對所考慮的假設、要優(yōu)化的目標和要整合的約束條件各不相同，且各有優(yōu)缺點.文獻[1]通過構(gòu)建最小化貨車訪問路線總成本的目標函數(shù)來實現(xiàn)靜態(tài)調(diào)運，采用迭代局部搜索的啟發(fā)式算法求解；文獻[2]提出若干有效不等式，建立了數(shù)學模型，利用禁忌搜索算法求解.由于調(diào)度周期長，最優(yōu)解局限于局部，部分文獻考慮調(diào)度周期的問題.文獻[3]為了滿足共享車快速響應調(diào)運和降低調(diào)運成本的需求，構(gòu)造了基于分形數(shù)的多車場協(xié)同調(diào)運模型；對動態(tài)調(diào)度，文獻[4]研究的是時變環(huán)境下，結(jié)合不同類型單車之間的替代特性，建立了混合整數(shù)規(guī)劃模型，并設計了混合禁忌搜索算法對問題進行求解；Kadri[5]提出了一個已知的閾值水平，表示每個站點平衡共享車數(shù)量，再平衡需求僅用于滿足閾值水平即可.文獻[5]采用一個平衡點，平衡操作次數(shù)較大，平衡時間較長.本文將站點的平衡定義為平衡區(qū)間，代替文獻[5-6]中的平衡點，站點內(nèi)的共享車庫存處于這個區(qū)間，都屬于平衡，可減少平衡次數(shù).另外，本文定義新的評價滿意度的指標函數(shù)-再平衡效益衡量函數(shù)，在此基礎上建立以總行程距離最小和再平衡效益衡量函數(shù)最大的雙目標函數(shù)，提出基于變領域搜索的粒子群-禁忌搜索算法對問題進行求解.

本文研究靜態(tài)共享車再平衡問題(SBRP).文章結(jié)構(gòu)是：第2節(jié)介紹了實用的平衡彈性間隔概念，在此基礎上定義站點平衡程度的指標-再平衡效益衡量函數(shù)，建立以路線最小化和再平衡效益衡量函數(shù)最大化的混合整數(shù)規(guī)劃雙目標模型，這是本文的主要內(nèi)容之一；第3節(jié)介紹粒子群-禁忌搜索算法，為避免陷入局部最優(yōu)，提高探索能力，引入3種結(jié)構(gòu)的變異算子；第4節(jié)主要是對改進的粒子群-禁忌搜索算法進行收斂性分析.

1 BBS平衡問題描述和數(shù)學建模

混合整數(shù)非線性規(guī)劃模型是經(jīng)典的求解路徑最短問題模型，下面是標準的規(guī)劃模型[7]：

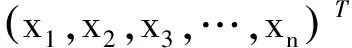
由于整數(shù)問題較難求解，將INLP問題轉(zhuǎn)化成其相應的松弛問題NLP,即不考慮決策變量的整數(shù)要求，

1.1 平衡彈性區(qū)間

在以往的研究中，BSS站的平衡被定義為一個預先指定的平衡點，即站點共享車數(shù)量需要達到預定的數(shù)量，如文獻[5-6]采用這種定義方法.這種定義法需要多次平衡操作，平衡時間較長.本文將平衡點擴展到平衡區(qū)間，共享車數(shù)量落到預定平衡區(qū)間，可視為達到平衡，這種定義法可減少平衡時間，減少旅行成本.

當α=0時，平衡間隔區(qū)間為平衡點，是平衡間隔區(qū)間的一個特例.顯然，α的值不同會導致平衡區(qū)間的大小不同.一條訪問路線的各站點庫存情況如表1所列.假設站點j的目標庫存為30，α=0.2.采用平衡間隔后，平衡區(qū)間為[24,36]，則1、2、4、14站的庫存處于平衡區(qū)間.

表1 站點庫存情況

另外每個站點既需要足夠的共享車以滿足用戶的租賃需求，又需要足夠的空位來滿足用戶歸還共享車的需求.因此，站點服務功能包括共享車租賃功能和歸還功能.

1.2 再平衡效益衡量函數(shù)

Li[9]考慮未滿足需求的懲罰函數(shù).本文考慮將未滿足需求的懲罰轉(zhuǎn)換成滿足需求的程度，表現(xiàn)為共享車租賃功能和歸還功能的使用程度.

站點可分為3個間隔：(0,(1-α)aj]，((1-α)aj,(1+α)aj]，((1+α)aj,Hj].在左側(cè)間隔內(nèi)，當車站為空時，共享車不能租用，所有插槽都可返回，因此租賃能力為0，返還能力是1.隨著共享車數(shù)量的增加，租賃能力也增加了，也有足夠的空地來滿足用戶的退貨請求，返還能力仍然是1.當共享車的數(shù)量增加到(1-α)aj時，有足夠的共享車出租，租賃能力增加到1，返還能力仍然是1.左側(cè)間隔內(nèi)站點服務能力取決于租賃能力.在中間間隔，即平衡間隔內(nèi)，車站有足夠的共享車和足夠的空地，所以站點的服務能力保持在1.在右側(cè)的區(qū)間內(nèi)，如果共享車增加，租賃能力保持在1，但空置空間越來越少，返回能力減少.當車站車滿了，租賃能力仍然為1，返回能力變?yōu)?.右側(cè)間隔內(nèi)的站點服務能力取決于返回能力.

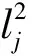
再平衡效益函數(shù)在三個間隔(0,(1-α)aj]、((1-α)aj,(1+α)aj]、((1+α)aj,Hj]上的值越大，說明需求滿足的程度越高，站點服務能力越好.

1.3 模型的建立

本文重點考慮訪問站點的旅程和站點服務能力，建立雙目標函數(shù).該函數(shù)定義在完全圖G=(V,A)上，A={(i,j)}是路線弧的集合，dij是頂點i和頂點j之間的距離.如果車輛從站點i行駛到站點j，二元決策變量xij=1；否則xij=0，決策變量xij是0,1整數(shù)變量.變量yij表示在弧線(i,j)∈A上流動的共享車的數(shù)量，yij也是整數(shù)變量.

本文在平衡彈性區(qū)間的基礎上建立模型：

(1)

(2)

(1)是行駛路線最小化；(2)是再平衡效益指標函數(shù)最大化.變量滿足如下約束條件：

(3)

該條件確保每個站點必須恰好訪問一次.

(4)

規(guī)定進入和離開j站的流量之間的差等于再平衡需求.

(5)

該條件確保一個站點只進行交付或者收集這兩種操作之一.

(6)

該條件確保在站點收集的車輛不能超過車輛的剩余量.

(7)

該條件確保交付到j站的車輛不能超過再平衡操作車輛持有的庫存.

下面將(1)、(2)的可行區(qū)域進行松馳，形成兩個規(guī)劃問題：

(8)

(9)

顯然所有路徑之和是(8)的上界，無平衡操作是(8)的下界，則

是需求滿足程度的指標，每個站點的平衡滿足程度指標：

達到最大，使整體滿足程度變大，則

記

與單目標模型相比，多目標模型可以生成一組非支配最優(yōu)解，根據(jù)不同的實際情況選擇合適的方案.

2 粒子群-禁忌搜索算法

本文采用粒子群-禁忌搜索算法(TS-PSO)進行布局優(yōu)化，并在粒子群迭代過程中引入3種變異粒子，增加粒子群的多樣性，避免陷入局部最優(yōu).

假設在二維搜索空間中，有m個粒子組成一群體，第i個粒子在二維空間中的位置表示為xi=(xi1,xi2)，第i個粒子經(jīng)歷過的最好位置(有最好適應度)記為Pi=(pi1,pi2)，每個粒子的飛行速度為Vi=(vi1,vi2),i=1,2,…，m.在整個群體中，所有粒子經(jīng)歷過的最好位置為Pg=(pg1,pg2)，每一代粒子根據(jù)下面公式更新自己的速度和位置：

vid=wvid+c1r1(pid-xid)+c2r2(pgd-xid)，

(10)

xid=xid+vid，

(11)

其中：w為慣性權重；c1和c2為學習因子；r1和r2是[0,1]之間的隨機數(shù).

2.1 領域變異操作

為了增加粒子的多樣性，同時使搜索范圍變大，粒子隨機執(zhí)行3種結(jié)構(gòu)的變異，具體如下：

(1)隨機選取一個位置，將其從原位置移開，插入到另一個隨機位置；

(2)隨機選擇兩個位置，交換位置；

(3)隨機選擇幾個位置，按逆序排列.粒子變異操作后，如果新粒子優(yōu)于原粒子，則新粒子將取代原粒子;如果原粒子支配新粒子，則新粒子將被丟棄.否則，如果這兩個粒子之間沒有優(yōu)勢關系，則隨機選擇其中一個.通過改變站點的排列，可以確定一條新的車輛路線.為了生成初始解種群，可以采用上述隨機變異的方式形成不同的粒子.

2.2 改進算法設計

由于粒子群算法具有局部搜索能力弱，容易陷入局部最優(yōu)等缺點，本文對粒子群算法進行改進，提出一種粒子群-禁忌搜索算法(TS-PSO).

TS-PSO算法流程如下：

(1)初始化算法參數(shù)，隨機生成粒子的初始位置和速度；

(2)計算每個粒子的目標值f1*,f2*；

(3)對每個粒子，比較目標值f1*,f2*和目前的最優(yōu)f1(pbest),f2(pbest)，如果f1*f2(pbest)，則更新目前最優(yōu)pbest=pnow，T=N(pbest)；

(4)對每個粒子，判斷是否符合變異條件，如果符合進入步驟5；

(5)對pbest(j)進行變異操作，如果變異后的粒子目標函數(shù)值更優(yōu)，則保留變異，否則取消當前變異；

(6)將所有粒子的最優(yōu)值中最優(yōu)的個體存儲在全局最優(yōu)gbest中；

(7)更新每個粒子的位置和速度；

(8)進行邊界條件處理；

(9)判斷是否滿足粒子群迭代終止條件，若是，則結(jié)束粒子群算法迭代進入下一步；否則返回步驟2；

(10)將得到的最佳微粒解碼，進行禁忌搜索；

(11)禁忌搜索操作結(jié)束，輸出結(jié)果.

3 收斂性分析

粒子群-禁忌搜索算法是在二維搜索空間中進行，可選擇10塊平面區(qū)域，每塊區(qū)域設定800 m×800 m，隨機選擇一塊研究區(qū)域，在區(qū)域內(nèi)選擇潛在站點.潛在站點的選擇基于以下規(guī)則:①站點應位于距離重要交通樞紐(如火車站、公交終點站和地鐵站)和主要路口300～500m處；②站點應靠近較大的居住區(qū)、機關、企業(yè)、商業(yè)區(qū)、學校、醫(yī)院、旅游景點等；③站點應避免直接進入繁忙的機動車道和十字路口.基于上面原則選定60個潛在的共享車站點和一個倉庫.容量為Q的平衡車從倉庫出發(fā)開始訪問站點，一條訪問路線，即為目標函數(shù)的一條典型的解或者一個粒子.訪問站點的同時也對站點進行再平衡.

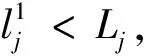
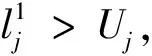
算法流程如下：

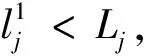
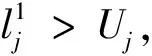
表1是包含15個站點的訪問路線和站點庫存.若共享車數(shù)量在平衡間隔內(nèi)，則該站點可以視為處于平衡狀態(tài)，不需要重新平衡.沿用2.1的假設，站點j的目標庫存為30，α=0.2，平衡區(qū)間為[24,36].對于不平衡的站點用平衡車再平衡，具體平衡結(jié)果如表2所列.訪問路線如表2的第一行.其中“+”表示提貨再平衡需求，“-”表示配送再平衡需求.

通過再平衡，可使其余站點達到平衡.從表2可以看出10、12站未達到目標庫存，但已經(jīng)在平衡間隔內(nèi)，再平衡程度相對滿意，這也體現(xiàn)了平衡間隔的優(yōu)勢.

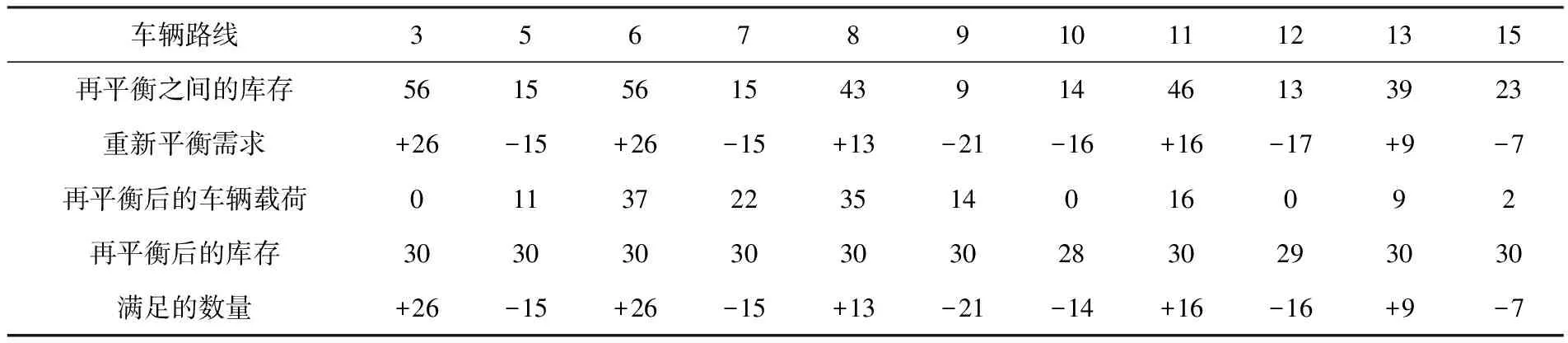
表2 初始解決方案的一個示例

4 結(jié)語

本文引入平衡區(qū)間和再平衡效用函數(shù)，建立雙目標函數(shù)，提出粒子群-禁忌搜索算法，加入三種變異粒子，改進了算法，使得平衡次數(shù)和時間變少.由于α的不同會影響平衡區(qū)間及目標函數(shù)，下一步會探討不同的參數(shù)值對目標函數(shù)的影響.