具有加入最短隊列規則的Jackson網絡的性能分析

程慧慧，辛超楠

(華北水利水電大學 數學與統計學院，河南 鄭州 450046)

0 引言

排隊網絡是一類重要的排隊模型，在實際中應用廣泛.很多學者經常通過減少隊列長度，縮短顧客等待時間或提高系統服務速率來提高排隊網絡的性能，比較常用的研究方法是加入最短隊列規則(join the shortest queue,JSQ).

Ephremides 等[1]提出：當到達的顧客被分配到兩個相似的指數服務器之一時，在已知兩個服務器上的隊列長度時，最佳決策是將顧客分配到較短的隊列.Johri[2]證得JSQ規則最小化了服務速率依賴于狀態的排隊系統的顧客數和等待時間.當排隊系統中的隊列數目N較大時，在引入JSQ規則后會變成高維的交互系統，這樣的排隊系統可以利用平均場模型來研究.平均場理論最早應用于統計物理[3-4]，其優點是可以通過求確定性系統的解來研究排隊系統的一些性質.Dawson等[5]針對隊列間具有交互作用的大型排隊網絡，利用平均場近似的方法研究了排隊網絡的極限特征及其平穩分布.Dawson等[6]針對具有JSQ規則的大型排隊網絡，利用平均場近似研究了排隊網絡的一些極限特征，并證實了在JSQ規則下排隊網絡的性能得到了提高.

Jackson網絡是一種經典的排隊網絡[7]，由J.R.Jackson[8]于1957年提出.Jackson網絡廣泛應用于計算機系統和調度問題中[9-11]，因此研究如何提高網絡的性能這一問題就顯得非常有必要.Martin等[12]對經典的Jackson網絡進行修改，使每個節點具有N個隊列，顧客到達一個節點后隨機地選擇m個隊列，然后加入m個隊列當中最短的一個，證得此時排隊網絡的平穩分布呈超指數收斂，并且縮短了隊列的平均隊長.Azaron等[13]通過優化控制Jackson網絡中所有節點的服務速率和到達速率，使得網絡最短路徑的期望值最小.Xia[14]研究了開放Jackson網絡的準入控制問題，證明了最優控制策略具有閾值形式.Imry等[15]在開放Jackson網絡中利用節點生成法，得出了使系統的平均作業數和響應時間最小化的服務速率的再分配方法.Timmer等[16]考慮了一個具有獨立節點的Jackson網絡，每個節點可以通過調節顧客總的到達率(不依賴于狀態)來減少排隊系統總的預期等待時間.Ansorena[17]利用封閉Jackson網絡模型，得到了使碼頭運營利益最大化的具體方案.晉良海等[18]通過構建安檢系統的Jackson排隊網絡模型，優化安檢系統服務參數，縮短了旅客提取行李的平均等待隊長.

目前關于Jackson網絡的研究基本上都是時齊的，對非時齊的Jackson網絡的研究較少.本文在文獻[5-6]的啟發下，將JSQ規則引入具有大量節點的Jackson網絡中，利用平均場近似的方法研究非時齊Jackson網絡的相關性質.

1 模型簡介

假設Jackson網絡中含有J個節點(J很大但有限).在節點i∈{1,2,3,…,J}處，單位時間內從系統外部進入該節點的顧客數服從參數為λ′的泊松分布，顧客在該節點接受服務的時間服從參數為μ的指數分布.在第i個節點接受完服務后立刻以pij的概率進入第j個節點，并在那里等候接受服務，或者以pi0的概率離開系統，

記P:=(pij)，pij表示從節點i到節點j的轉移概率，并且有一到達率為Jλs的泊松到達流，顧客從該到達流加入排隊網絡中的最短隊列.

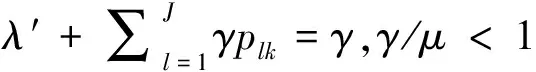
設E={0,1,2,…}，T≥0，DT(E)(D∞(E))

表示從[0,T]((0,∞))到E的右連續且具有左極限的函數空間.記Xt(ω)=X(t,ω)=ω(t)，也可以記做X(t)=X(t,ω)，其中ω∈DT(E).Ft=σ{X(s),0≤s≤t}表示由{X(s),0≤s≤t}生成的最小σ代數，F=σ{X(t),t≥0}表示由{X(t),t≥0}生成的最小σ代數.P(D∞(E),F)表示(D∞(E),F)上的全體概率測度的集合.Pp(E)表示E上的p階矩有限的概率測度的集合,p∈N+.P(E)表示E上的所有概率測度的集合.

2 平均場近似

到達速率為λi，服務速率為μi,i=1,2,…的M/M/1隊列的隊長過程{Y(t),t≥0}是一個生滅過程，對應的Q矩陣為

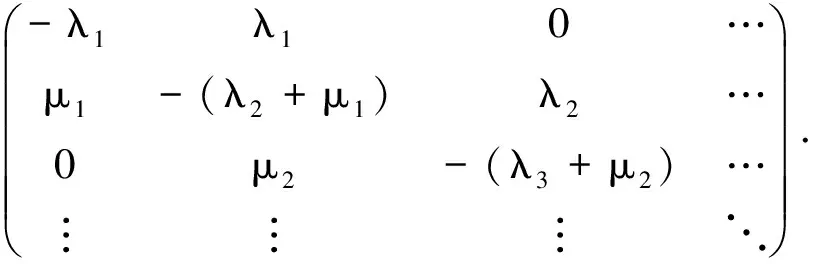
對應的算子Ω為

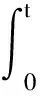
針對前面所描述的交互系統，記X(J)(t)=(X1(J)(t),…,XJ(J)(t))，其中Xk(J)(t)表示節點k處的顧客數量，k=1,…,J.X(J)(t)的概率分布為P(J)∈P(D∞(EJ)).令x=(x1,…,xJ)∈EJ，EJ表示E的J維笛卡爾積，則X(J)(t)的轉移速率為

其中：#A表示集合A中元素的個數；1A(·)表示集合A上的示性函數；當A是一個單點x時，有1A=1x.

網絡對應的算子為

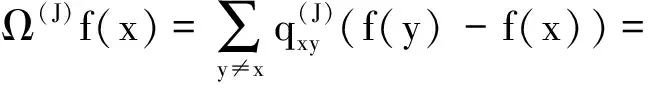
其中，ek是第k個分量為1，其余均為0的J維向量.

首先定義交互函數h:E×P(E)→R+:

其中ms(ν)=min{k≥0,ν({k})>0}表示概率測度ν在E上的支集的最小點.下面引入非線性主方程：

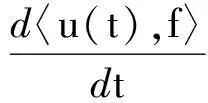
(1)

其中〈ν,f〉表示f與ν的積分.

且有

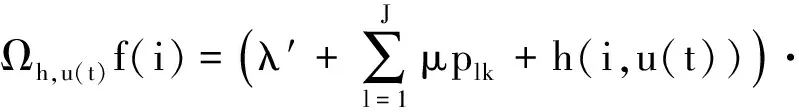
(2)

因為每個節點具有相同的作業規律，所以通過研究節點k來研究排隊系統的相關性質，方便起見稱之為典型隊列.

定義1假設u∈P(E)，如果ut(·)=P°Xt-1(·)滿足非線性主方程(1),且u0=u，P的初始分布為u，則稱P∈P(D∞(E),F)為非線性主方程的解.如果對任意的j∈E，有

P(Xt+s=j|Ft)=p(t,Xt;t+s,j),

其中轉移函數滿足

則P是馬爾可夫解.

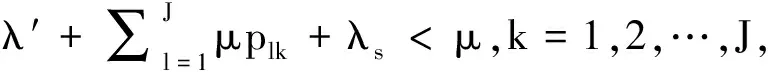
(a)如果定義

則

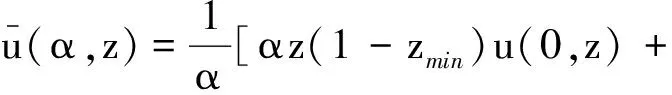
(3)

其中

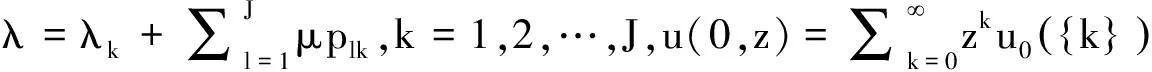
(b)如果u0({0})=1，則

(4)

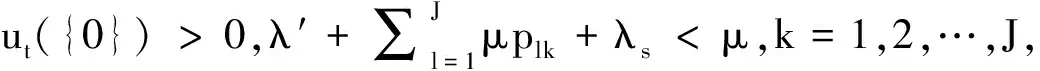
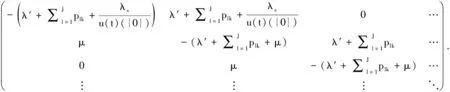
(5)

其中u(t)(·)=P°X-1(t)(·).

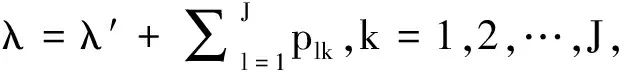
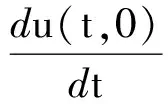
(6)

這一微分方程組與文獻[6]中的式(7)一致，同理可得結果(a).其中拉普拉斯變換保證了解的唯一性.

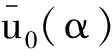
針對交互系統X(J)(t)=(X1(J)(t),…,XJ(J)(t))，定義

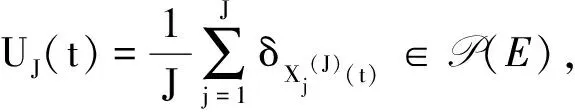
(7)

δx表示在單點x處的狄克拉測度.{UJ(t)}t≥0描述了隊長的經驗分布的變化過程；PJ表示經驗測度過程{UJ(t)}t≥0的概率分布.

定義2假設u∈P1(E)，如果滿足以下條件：

1)P°X0-1=u；

2)P°Xt-1=ut；

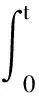
(Xs)ds,Ft,P)是鞅.

則稱P∈P(D∞(E),F)是鞅問題[u,Ω‖ut‖]的解.

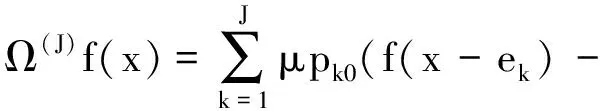
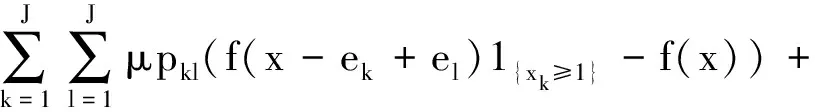
引理得證.

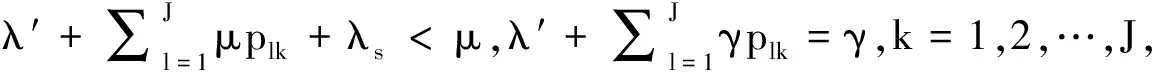
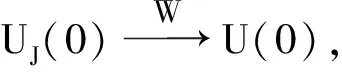
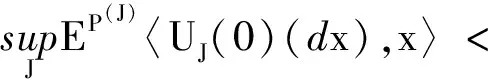
(8)

由引理1可得

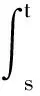
取s=0，可得

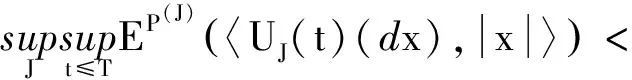
(9)

設

PJ(E)=

UJ(t)是D∞(PJ(E))上的馬爾可夫測度值過程,該過程的轉移速率矩陣為

對應的算子為

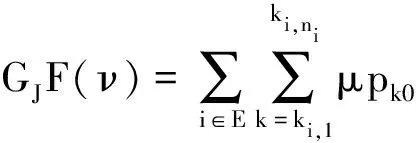
(10)

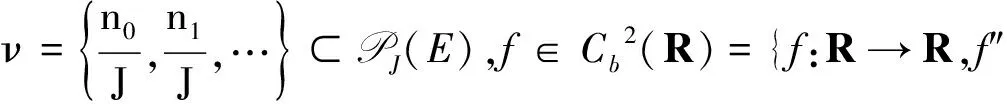
利用泰勒公式可得

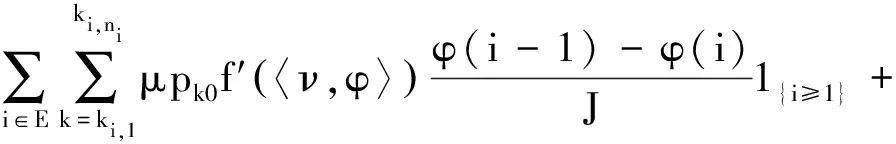
(11)

整理得

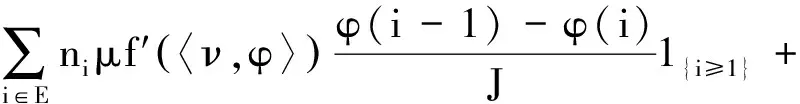
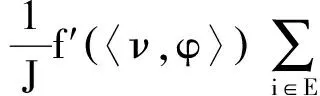
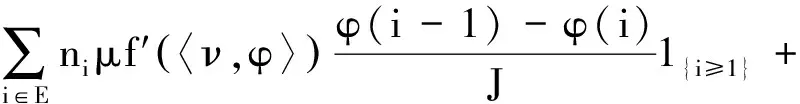
(12)

因為{UJ：J≥1}在D∞(PJ(E))上是弱緊的，所以對任意的{J′}?{J},存在{J″}?{J′}，使得UJ″弱收斂到U.當J趨于無窮時，由式(9)和(12)可知P∞是以G為生成元的鞅問題的解，

GF(ν)=f′(〈ν,φ〉)〈ν,Ωh,νφ〉.

令f(x)=x和f(x)=x2，可得

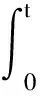
與文獻[19]中的定理1.1的證明過程相似.因此可知U(t)是非線性主方程(1)的解，由命題1可知解是唯一的，定理證明完畢.

3 平穩分布

定理2在JSQ系統中，假設λ+λs<μ，則唯一的平穩分布為

π0JSQ=1-ρ,πkJSQ=ρ(1-σ)σk-1,k≥1，

(14)

其中：

證明由定理1可知極限典型隊列在時刻t的Q矩陣可表示為

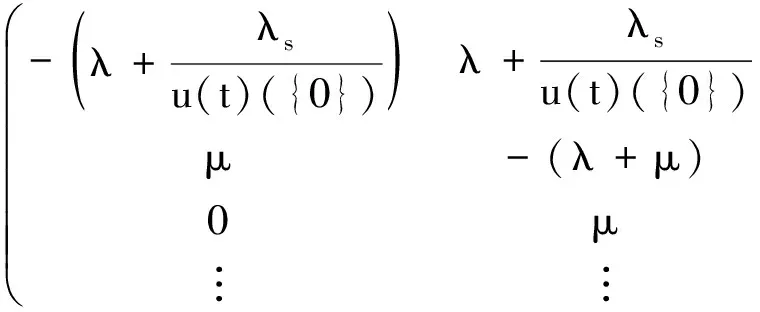
在平穩條件λ+λs<μ下，如果時間t趨于∞，則

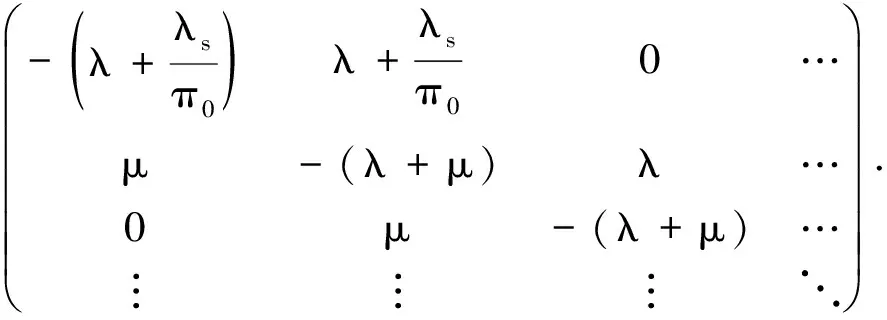
由πQ=0，π=(π1,π2,…)可得

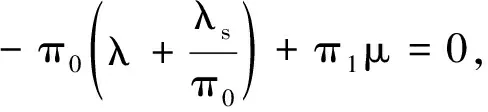
所以

最終可得

證畢.

如果一個智能客戶可以隨機地加入一個隊列，則對應的Q矩陣為

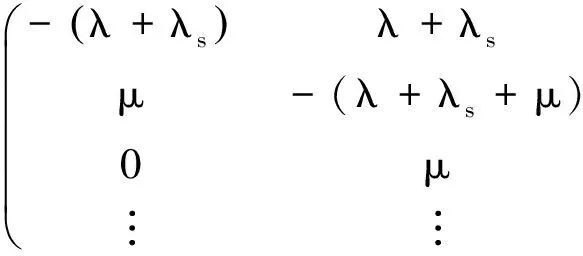
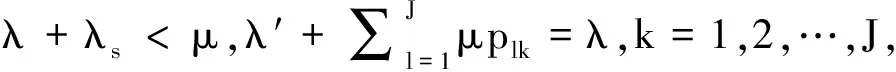
(15)

對JSQ系統和J∞Q系統的平穩分布進行對比可得：

(1)π0JSQ=π0J∞Q，兩個系統的空閑率是相等的.通過計算可得JSQ系統和J∞Q系統的平均到達率和平均服務速率均相等，因此空閑率相等.平均到達率為

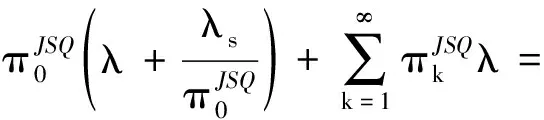
平均服務速率為

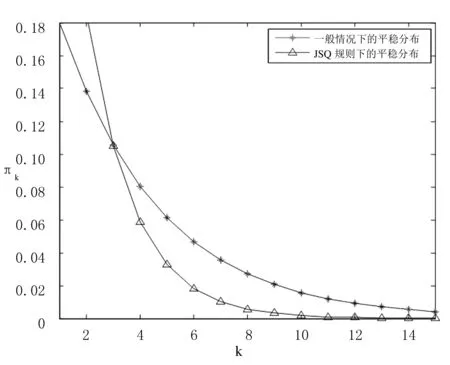
圖1 JSQ系統與J∞Q系統的平穩分布對比

由圖1可得，存在k0，當1≤kπkJ∞Q；當k≥k0時，πkJSQ<πkJ∞Q.

(3)JSQ的平均隊長小于J∞Q的平均隊長.

JSQ的平均隊長為

J∞Q的平均隊長為

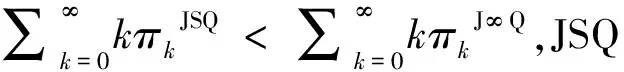
綜上所述，JSQ規則下的Jackson網絡的性能得到了提高.

4 結語

將加入最短隊列規則引入Jackson網絡中，建立了一個平均場相互作用模型，從極限結果的角度研究了該網絡的性能.結果表明：隊列長度的經驗分布收斂到非線性主方程的唯一解；將加入最短隊列模型和智能到達者隨機加入J個隊列中的任意一個的模型進行對比，得出加入最短隊列規則提高了Jackson網絡的性能.