基于模糊PID控制的工程車輛機械液壓控制策略研究

闞玉錦,蘇 進,丁響林

(安徽機電職業技術學院 機械工程學院,安徽 蕪湖 241002)

近年來，國家對基建施工的質量、環保與安全的要求越來越嚴格，傳統工程車輛的機械液壓控制方法已經不能滿足當下高標準的需求[1].比如傳統的PID控制算法，雖然具有部署及運用簡單等優點，而且在大多數機械運動控制系統里，其控制效果已經足夠滿足工程要求，是目前工程上使用最為廣泛的控制算法，但是該算法具有在某些情況下不能忽視的缺陷.比如對被控對象的數學模型依賴程度大，對非線性對象控制效果不佳等.行業相關研究多傾向于對車輛本身部件進行改進來優化控制效果，此種方式成本較大.因此，從現有方法進行改進以提高對工程機械的控制效果，有一定研究價值[2].

1 基于模糊PID控制的工程車輛機 械液壓控制方法設計

1.1 模糊PID控制算法構建

在工程建設領域，很多有特殊作業要求的工程車輛機械，比如需要保證行駛穩定的路面攤鋪機、瀝青灑布車、路面銑刨機等[3].然而，由于施工現場的各種不確定因素和負載的隨機性、系統性波動，傳統的控制方法已經難以滿足對工程車輛穩定行駛的控制需求[4-7].針對這一矛盾，前人提出過多種解決方案，比如使用PID控制，雖然運用廣泛，但在某些情況下也有不能忽視的缺陷[8]，控制效果受部件的數學模型質量好壞影響程度大，泵控馬達速度控制系統在一般情況下具有延遲性，作用機理復雜，且工作過程中狀況復雜多變，因此難以使用數學建模方法將其核心工作流程抽象提取出來，導致PID控制算法無法快速準確地達到控制要求[9-11].

新興的智能控制技術為解決這類難題提供了新思路，特別是其中的模糊控制法，其魯棒性、穩定性優良，對內在規律復雜或無法用數學語言描述的非線性復雜系統控制效果較好.但它無法消除系統穩態輸出值與目標值的偏差，基于此問題，本文研究將PID控制算法與模糊控制法融合來優化工程車輛的行駛穩定度[12]，構建模糊PID控制算法.PID控制中，設置期望值與反饋值的差值為e(t)，為適應計算機計算而離散化處理后的控制量u(t)表達式如式(1)所示.

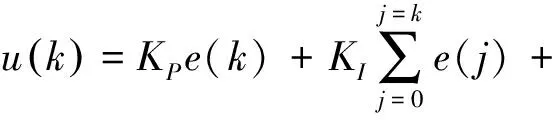
(1)

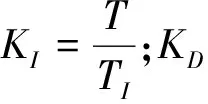
式(1)因為控制器的輸出與被控制對象的實際位置相互對應，也被稱為位置式PID，該特點導致控制器一旦出錯，就容易造成誤動作，甚至產生工程事故.為避免此缺點，需要對算法進行改進.為進一步簡化計算過程，提高序列計算效率，公式(1)還可被改寫成公式(2).

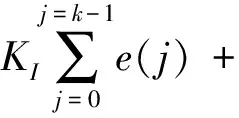
(2)

再將公式(2)減去公式(1)，即可得到增量式PID，如公式(3)所示.

Δu(k)=KP[e(k)-e(k-1)]+KIe(k)+KD[e(k)- 2e(k-1)+e(k-2)].

(3)

因此也可得出增量式PID控制器的輸出表達式：u(k)=u(k-1)+Δu(k).對比增量式與位置式PID，可發現，兩者在形式有較大區別，前者不存在積分操作，因而不會引起積分飽和，也就不需要對積分進行限幅，輸出計算的限幅即可.退一步分析，即便計算器運行出錯，由于控制器輸出對應著對象位置的變化量，誤動作造成的影響也會比位置式PID小.為了消除控制系統運行時產生的穩態誤差，大多數情況下還需要引入積分操作，由于控制器輸出還會受到PWM占空比極值影響，所以需要對PID控制器輸出做限幅處理，設控制器輸出的上下限值分別為umax和umin，則添加限幅操作后的控制器輸出值如公式(4)所示.

(4)

模糊控制法是通過把專家的經驗總結并轉換為計算機程序，即模擬人的思維方式來對對象進行控制的方法[13-14].其對內在規律復雜或無法用數學語言描述的非線性復雜系統控制效果較好，工作原理如圖1所示.

由圖1可知，模糊控制法的核心思想就是制定模糊控制命令，其依據是行業相關專家的成熟經驗，首先把模糊關系R通過相應計算規則解出，同時通過傳感器得到當前計算指標的測量值，根據兩者計算出偏差值e；再使用R把e轉換為模糊量E，結合運算規則對E進行推理，從而求出控制量U=E°R；最后對U使用反模糊規則轉化為一個精確的控制量u，發送給被控對象以執行相應控制操作.模糊控制也存在控制精度低、自適應能力有限等缺點，所以將增量式PID算法與模糊控制法融合起來，融合后的算法流程如圖2所示.

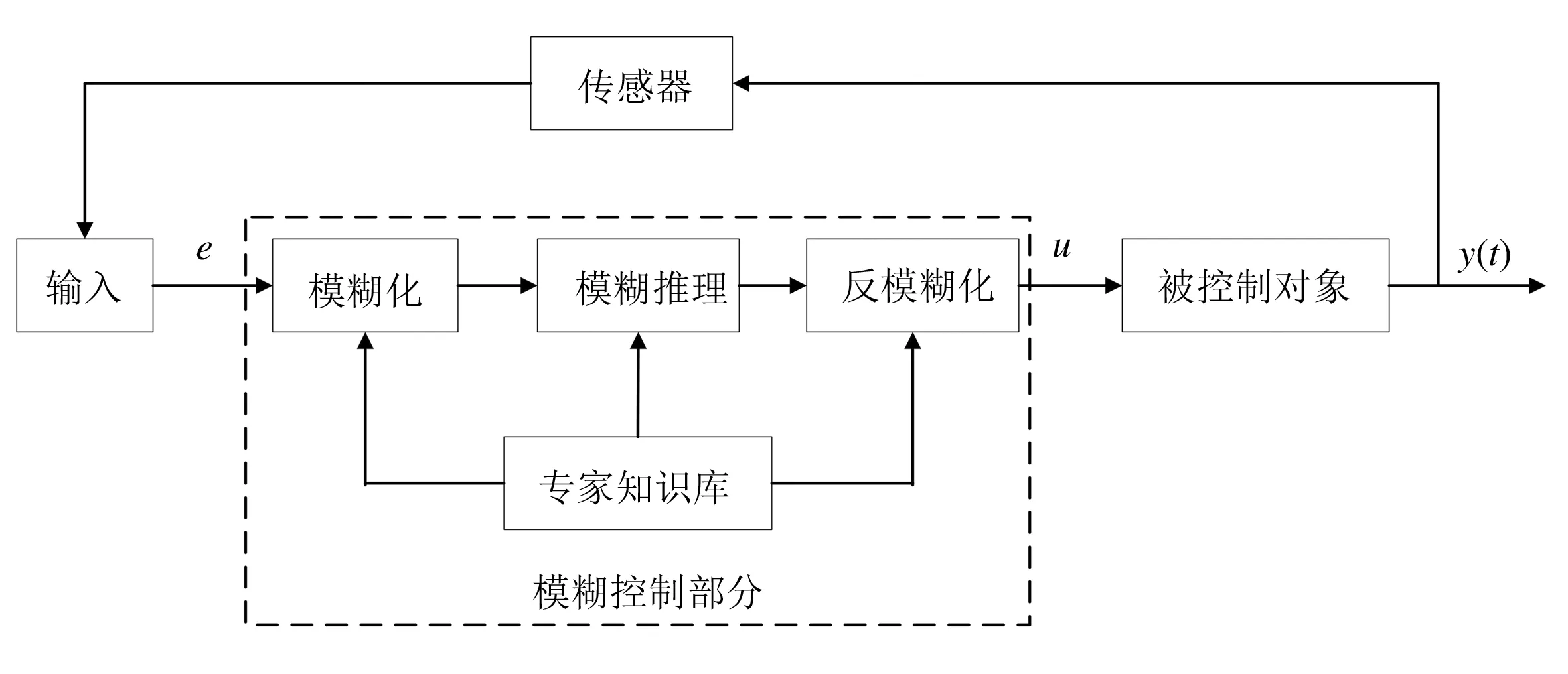
圖1 模糊控制法工作原理

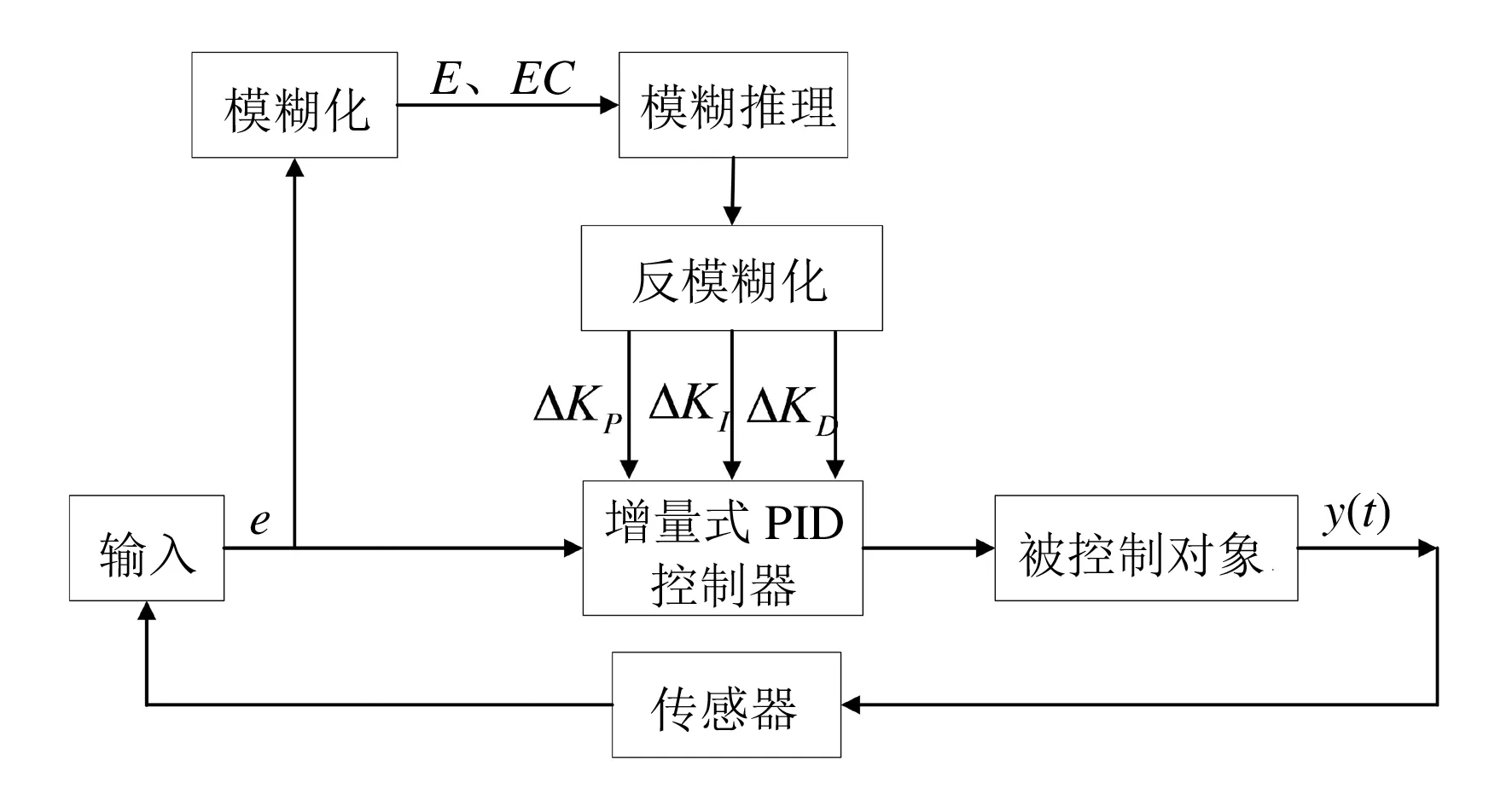
圖2 模糊PID算法的計算流程

由圖2可知，模糊PID控制器由PID控制器和模糊控制器兩部分組成，其核心思想是先將專家的PID參數轉化為模糊規則存入MCU部件，然后MCU通過實時誤差及其變化率將PID參數更新，達到讓被控對象運動更加穩定、流暢的目的.

1.2 工程車輛機械液壓控制系統的數學模型 構建

由于模糊PID算法的計算效果會受到研究對象的數學模型影響，因此本文主要以工程車輛機械液壓系統中的常見部件，即泵控馬達速度控制系統為對象，構建其數學模型.泵控馬達速度控制系統由三大核心組成部分，分別為速度傳感器、泵控馬達系統和變量機構，下面分別構建其數學模型[13-14].先對電液比例變量機構建模，電液比例變量機構的比例放大器電流I對偏差電壓E的傳遞函數、閥芯位移Xv對電液比例換向閥電磁鐵線圈電流Ibv的傳遞函數如公式(5)所示.

(5)

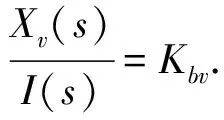
(6)

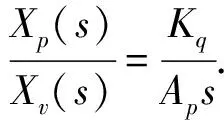
(7)

其中，Kqp為變量泵的流量增益(m3/s·rad)；Dm為馬達的排量(m3/rad)；V0為液壓回路的有效容積(m3)，Ct為系統總泄露系數(m5/N·m)；ωh為液壓固有頻率(rad/s)；ζh為液壓阻尼比；βe為有效體積的彈性模量(Pa).

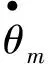
(8)

其中，Kf為反饋增益系數(V·s/rad).完成泵控馬達速度控制系統數學模型搭建后，就可形成完整的基于模糊PID控制的工程車輛機械液壓控制系統，該系統一般結構由控制器、模式切換、車速控制、發動機轉速控制和人機交互系統5大核心部分組成.其中控制器負責對各種輸入信號處理、實現對系統的控制，其核心就是本文提出的模糊PID控制算法.

2 基于模糊PID算法的工程車輛機 械液壓控制仿真實驗分析

為了驗證模糊PID算法對工程車輛機械液壓控制系統控制的車輛行駛穩定性優化效果，本設計選取在工程車輛市場上具有一定代表性的SX1254BM434型載貨汽車的車輛底盤為研究對象，并選用TMS320F28335型32位浮點DSP處理器，結合建立的數學模型，采用MATLAB編寫腳本進行工程車輛行駛穩定性的仿真實驗.仿真實驗中涉及參數的值如表1所列.

表1 仿真試驗參數表

根據表1所列數值設置好實驗所需各參數后，再結合數學模型使用MATLAB建立工程車輛行駛的仿真系統.在實際工程現場中，工程車輛常用一檔來進行行駛移動，且常常會受到各種負載干擾.因此仿真實驗也以一檔為行駛條件，將其行駛速度設置為2 km/h，同時將在行駛4 s后對其作用一個大小500 N·m的負載干擾信號.運行實驗并整理數據后得到改進算法與原始算法控制下的速度階躍相應曲線，結果如圖3所示.

由圖3可以發現，在起步加速階段，使用傳統PID算法控制，系統速度達到峰值耗時0.82 s，最大超調量為13.36%，調整到設定速度耗時2.23 s，而使用模糊PID算法系統，速度達到峰值耗時0.83 s，與PID控制相差不大，最大超調量6.94%，比PID控制減少了48.05%，穩定耗時1.78 s，比PID控制算法縮短了20.18%.在負載作用階段，使用傳統PID算法時，系統的調整耗時是1.46 s，速度最大超調量為13.52%，而采用模糊PID算法時，系統調整耗時1.07 s，速度最大超調量為8.11%，分別比前者減少了26.71%和40.01%.以上數據充分說明，采用模糊PID控制算法比起傳統PID算法，能明顯提高系統的穩定性和反應速度.使用模糊PID控制時，車輛加速快慢對行駛穩定性的影響情況如圖4所示.圖4為采用模糊PID算法時，分別加速0.6 s、0.8 s、1.0 s和1.2 s達到1檔設定的速度響應曲線.

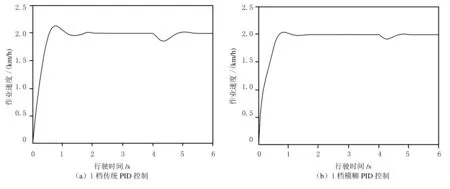
圖3 車輛行駛時有負載擾動的速度階躍響應曲線

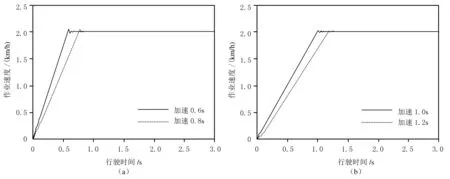
圖4 不同加速時間下系統的速度響應曲線圖

由圖4可知，加速時間為0.6 s、0.8 s、1.0 s和1.2 s時，車輛速度從加速完成到穩定狀態耗時分別為1.22 s、1.27 s、1.31 s、1.36 s和1.40 s，超調量分別為3.3%、2.8%、2.2%和2.7%.容易看出，加速時間越長，速度波動越小，行駛越平穩，但加速時間也不宜過長，否則會影響施工效率，應該結合工程的具體情況設置合適的加速時間.

3 結論

針對工程車輛機械液壓的控制問題，本文提出了一種融合模糊控制與PID控制的混合模糊PID控制算法，將輸入信號先輸入模糊控制器處理，再反模糊化輸出給PID控制器實現兩者的融合.為了驗證算法的有效性，選取工程車輛機械液壓系統中的常見部件，泵控馬達速度控制系統對其構建數學模型.以SX1254BM434型載貨汽車的車輛底盤和TMS320F28335型處理器硬件數據為基礎，通過MATLAB進行仿真實驗.實驗結果顯示，在起步加速階段，使用模糊PID控制算法，系統最大超調量6.94%、穩定耗時1.78 s，分別比PID控制算法的減少了48.05%與20.18%.在負載作用階段，使用模糊PID控制算法，系統調整耗時1.07 s，速度最大超調量為8.11%，分別比傳統PID控制算法減少了26.71%和40.01%.實驗證明，采用模糊PID控制算法比起傳統PID算法，能明顯提高工程車輛的變速與行駛穩定性.