風致飛擲物沖擊建筑浮法玻璃試驗和數值模擬

陳 勝， 黃 鵬， 顧 明

(同濟大學 土木工程防災國家重點實驗室，上海 200092)

大量的風災災后實地調查表明，風災中建筑的破壞形式多是圍護結構失效破壞。玻璃門窗等建筑圍護結構在風災中可能受到風壓和風致飛擲物沖擊雙重作用，其中風壓荷載為均布荷載，較難直接造成玻璃圍護結構的破壞，而風致飛擲物的沖擊作用為集中荷載，容易穿透玻璃門窗使其失效。尤其是對低矮建筑而言，其由浮法玻璃構成的門窗等圍護結構在風災中極易遭受風致飛擲物的沖擊破壞[1-2]。

在建筑風災破壞評估中，對風致飛擲物的研究問題可以概括成三類，分別是風致飛擲物的產生及起飛，飛行軌跡，以及對建筑圍護結構的沖擊效應[3]。現有的研究大部分集中在飛擲物的起飛條件和飛行軌跡[4-6]，而對飛擲物的沖擊效應關注較少。特別是在判斷建筑玻璃是否會破壞時，只是簡單地對比風致飛擲物沖擊時的動量或者動能與玻璃強度的大小，并未考慮風致飛擲物的外形、沖擊姿態等特性對破壞結果的影響。因此，為了準確評價由玻璃構成的門窗等建筑圍護結構受風致飛擲物沖擊后的破壞概率，進一步完善風災風險評估系統，有必要對風致飛擲物沖擊建筑玻璃的破壞特點進行更深入地研究。

目前，研究玻璃在沖擊荷載下破壞的方法主要有理論分析、試驗和數值模擬三種。在理論研究方面，研究人員提出了威布爾模型、隨機模擬模型、Rankine準則和非局部失效準則等描述玻璃失效的概率模型[7-8]，但是這些模型與玻璃的實際破壞情況相差較大。試驗是評價玻璃抗沖擊性能最可靠的手段，目前世界上大部分規范評估玻璃抗沖擊性能的手段都是依賴于特定的試驗方法[9-10]。但是，沖擊試驗需要花費巨大的經濟和時間成本，特別是風致飛擲物本身的一些特性，例如飛擲物的外形、飛行速度、沖擊姿態和沖擊位置等因素都可能影響破壞結果，而用試驗的方法研究全部這些因素存在很大的難度，因此需要考慮使用更加高效的數值模擬方法進行風致飛擲物沖擊建筑玻璃圍護結構的研究。

LS-DYNA是當前最著名的通用顯式動力分析程序，特別適合求解各種二維、三維非線性結構的高速碰撞、爆炸和金屬成型等非線性動力沖擊問題[11-12]，目前大部分研究人員均采用其模擬玻璃的碰撞問題。Timmel等[13]提出了利用LS-DYNA模擬夾層玻璃物理模型，將玻璃層當作脆性材料，夾層認為是超彈性材料，著重介紹了超彈性材料夾層的多種本構關系。劉奇等[14]采用LS-DYNA對汽車擋風夾層玻璃受沖擊荷載進行有限元模擬，分別用不同的材料模型模擬玻璃層和夾層材料，并設置了玻璃的失效應力和應變準則，最后通過試驗驗證了其模型能夠較好的模擬玻璃的失效模式。Zhang等[15]基于LS-DYNA建立了桿狀風致飛擲物沖擊夾層玻璃的數值模型，并利用該數值模型研究窗戶玻璃的易損性與夾層玻璃的尺寸、夾層厚度以及飛擲物的質量、撞擊速度等變量的關系。

雖然國內外學者對玻璃抗沖擊性能已經進行了大量的研究，但是仍然存在一些不足：① 目前對玻璃抗沖擊性能的研究多集中在材料、汽車等學科領域，而風工程對建筑玻璃抵抗風致飛擲物沖擊的研究還比較少；② 在研究沖擊物對玻璃破壞的影響因素中，大部分研究僅考慮了沖擊物的質量和速度兩個變量的影響，而忽略了風致飛擲物的形狀、沖擊姿態和沖擊位置等因素的影響；③ 目前研究的玻璃類型多是夾層玻璃，普通民用建筑玻璃(浮法玻璃)的抗沖擊性能少有人關注，而在實際的風災破壞中，這類玻璃是最容易受損的建筑玻璃類型。

本文首先進行了鋼球沖擊建筑浮法玻璃的破壞試驗,并基于LS-DYNA建立了浮法玻璃面板在沖擊荷載作用下的有限元模型。然后通過對比試驗和數值模擬的結果，驗證了飛擲物沖擊浮法玻璃有限元模型的準確性。最后，基于驗證后的沖擊有限元模型，以板狀飛擲物為代表，通過數值模擬方法研究風致飛擲物的外形、沖擊位置和沖擊姿態等特性對建筑浮法玻璃沖擊破壞效應的影響。

1 球狀飛擲物沖擊浮法玻璃的試驗和數值模擬

1.1 沖擊試驗

沖擊破壞試驗的材料包括沖擊物鋼球和被沖擊物浮法玻璃。鋼球采用直徑40 mm，質量261 g的實心軸承鋼鋼球，玻璃采用邊長為240 mm×240 mm，厚度分別為3 mm和5 mm的浮法玻璃面板。需要說明的是，玻璃面板四周各預留了20 mm作為邊界支撐的空間，所以玻璃面板在試驗中的凈邊長為200 mm×200 mm。

現實中建筑物門窗的玻璃面板通過結構膠與鋁合金框架相連接，其邊界條件較軟弱，故本文試驗采用木支架支撐浮法玻璃面板，并通過熱熔膠和夾具固定邊界，然后將固定好浮法玻璃面板的木支架通過螺絲固定在沖擊破壞試驗機的工作臺臺面上，如圖1所示。沖擊破壞試驗機由一個木質工作平臺固定一根鋼制立桿，桿上連接一根可自由升降的電磁吸盤組成。工作平臺平面用于錨固玻璃面板固定支架，并作為沖擊跌落的平臺。采用電磁吸盤控制鋼球下落，按下釋放按鈕即可使鋼球脫離電磁吸盤自由下落。通過升降電磁吸盤的固定桿位置可以自由調節鋼球的下落高度，高度調節范圍為0～2 700 mm，高度控制的精度為1 mm。

圖1 浮法玻璃沖擊破壞測試系統Fig.1 Impact failure testing system of the float glass

首先將鋼球最初距離玻璃面板的高度調為700 mm，然后釋放鋼球使其自由下落，沖擊點應位于玻璃面板的正中心位置，觀察玻璃面板是否被鋼球破壞并出現裂紋。如果玻璃面板被破壞了，記錄下鋼球的下落高度和玻璃面板的裂紋形式。如果玻璃面板沒有破壞，將鋼球距離玻璃面板的高度提高100 mm再次沖擊玻璃面板并觀察破壞情況，依此類推，直到玻璃面板被鋼球沖擊破壞。最后，根據自由落體運動方程(式(1))，由鋼球沖擊浮法玻璃面板的破壞臨界高度計算鋼球沖擊破壞臨界速度。

(1)

1.2 有限元分析模型

本文基于LS-DYNA建立和計算鋼球沖擊浮法玻璃的有限元模型，并通過HPERVIEW進行可視化后處理。球狀飛擲物采用直徑40 mm的鋼球，網格尺寸為2 mm，浮法玻璃尺寸為200 mm×200 mm×3 mm和200 mm×200 mm×5 mm，網格尺寸為1 mm×1 mm×1 mm，鋼球的撞擊位置為玻璃板平面的正中心，三維模型如圖2所示。

圖2 鋼球沖擊浮法玻璃有限元模型Fig.2 Finite element model of the float glass panel about to be impacted by the steel ball

由于本文僅關注風致飛擲物沖擊建筑玻璃的過程，不考慮飛擲物的飛行軌跡，故將鋼球與玻璃面板的初始距離設為0.5 mm。然后賦予鋼球不同的初始速度，從而確定鋼球破壞玻璃面板的臨界速度。定義鋼球和玻璃板的接觸類型為面面接觸(surface to surface)，接觸過程為侵蝕接觸(eroding contact)。單元類型采用8節點六面體實體單元Solid164，單元算法采用缺省的常應力單元計算公式。為了避免沙漏能對結果產生影響，通過定義關鍵字*CONTROL_ HOURGLASS對模型中可能產生的沙漏能進行控制。約束玻璃四邊的所有自由度，即邊界條件為四邊固支。

材料本構模型的選擇是有限元模擬中最關鍵的部分。由于本文主要研究的破壞對象是浮法玻璃，鋼球主要提供了沖擊荷載的作用，并且鋼的剛度遠大于玻璃的剛度，因此可以將鋼球近似模擬成剛性材料，本構模型為MAT_RIGID，主要材料參數如表1所示。

表1 鋼球材料參數(MAT_RIGID)

玻璃是一種典型的脆性材料，其應力應變關系是非線性的，這是由于玻璃內部和表面存在微裂紋和不均勻區，受力時微裂紋將急劇擴展從而引發整個構件破壞，而非均勻性對裂紋擴展方向和貫通模式有重要的影響。因此目前多采用損傷力學方法研究玻璃等脆性材料的微觀力學性能，并基于應變等價理論描述玻璃的應力應變關系[16]。JH-2(Johnson Holmquist ceramic constitutive model)模型被認為是最能夠體現玻璃和陶瓷等脆性材料力學特征的有限元動態本構模型。Cronin等[17]歸納了以往文獻[18-20]中提出的JH-2模型參數，并將JH-2本構模型數值模擬得到的結果與試驗結果進行對比，發現二者擬合良好，證明了JH-2本構模型的可靠性。因此，本文選取JH-2本構模型模擬浮法玻璃的材料特性，根據文獻建議，本文浮法玻璃的材料參數如表2所示。

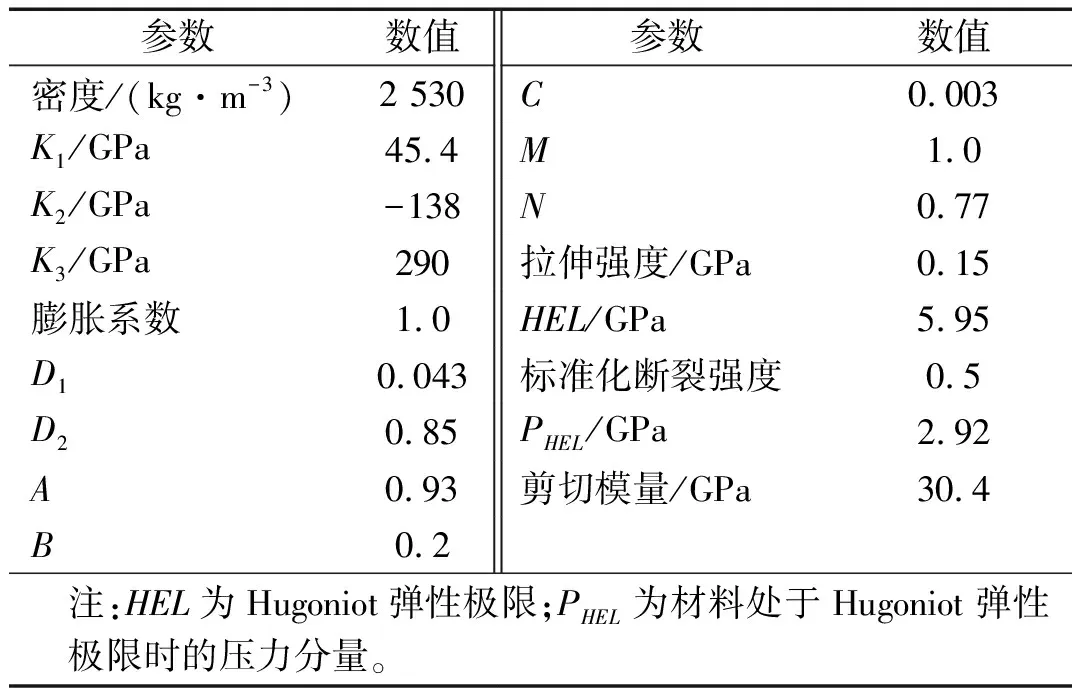
表2 浮法玻璃材料參數(JH-2)

1.3 試驗和數值模擬結果對比

為了模擬玻璃受沖擊作用后出現裂紋或破壞的結果，需要在其有限元模型中定義一個玻璃單元失效準則。本文采用最大主應力，即SIGP1作為玻璃單元的失效準則。需要注意的是，由于鋼球強度遠大于玻璃，不會在沖擊過程中破壞，因此對其不設失效準則。為了確定玻璃合理的最大失效主應力值，本文對SIGP1設定了不同的值進行鋼球沖擊浮法玻璃的有限元模擬，表3為200 mm×200 mm×3 mm和200 mm×200 mm×5 mm兩種尺寸浮法玻璃有限元模型采取不同的SIGP1失效準則得到的破壞結果及其與試驗結果的誤差。

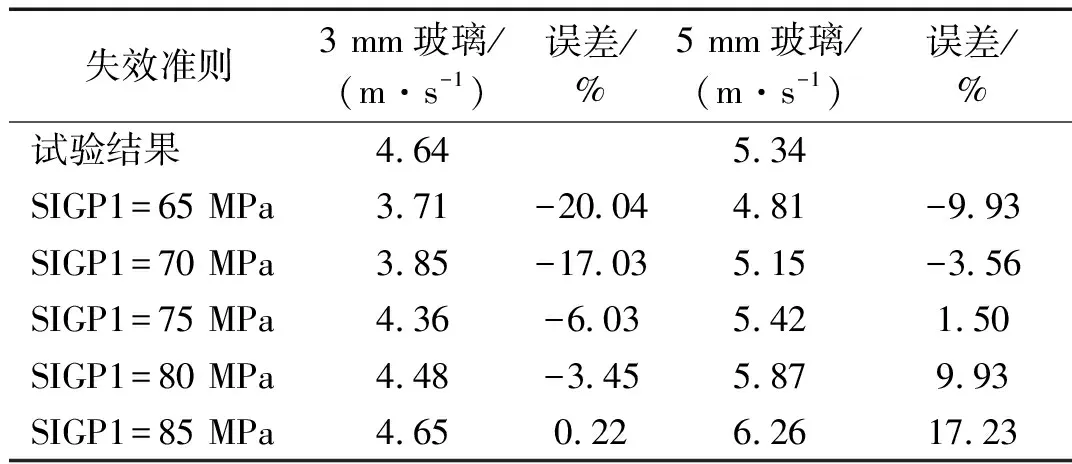
表3 玻璃不同失效準則對應的鋼球破壞臨界速度及誤差

由表3可知，將玻璃單元最大失效主應力值設為75 MPa，即SIGP1=75 MPa時有限元模擬破壞結果與試驗破壞結果最接近，此時3 mm和5 mm兩種厚度玻璃面板的誤差分別為-6.03%和1.50%，故本文采用SIGP1=75 MPa作為浮法玻璃在沖擊荷載下的失效準則。

圖3為數值模擬和試驗得到的3 mm和5 mm兩種厚度玻璃面板被鋼球沖擊破壞后的裂紋形狀和碎片飛濺情況對比。由圖3可見，玻璃面板破壞后的裂紋主要有放射狀和環狀兩種形式，其中又以放射狀裂紋為主。雖然數值模擬得到的裂紋數量和分布范圍小于實際結果，但是也出現了放射狀和環狀的裂紋形狀，能夠較準確地反映玻璃面板破壞后的裂紋特征。此外，數值模擬結果還較清晰地體現了玻璃面板受沖擊破壞后玻璃碎片飛濺的情況。

(a) 3 mm

(b) 5 mm

綜上所述，通過對比試驗和有限元數值模擬得到的浮法玻璃在鋼球沖擊作用下的破壞臨界值、裂紋形狀及玻璃碎片飛濺情況結果，發現二者的吻合程度都比較好，從而驗證了本文所建立的風致飛擲物沖擊浮法玻璃有限元模型具有較高的準確性。

2 板狀飛擲物沖擊效應的數值模擬

Wills等[21]根據風致飛擲物的三維尺寸將其大致分為球狀、板狀和棍狀三種類型，而板狀飛擲物是其中最復雜的飛擲物類型。這是因為不同于球狀和棍狀飛擲物，板狀飛擲物外形多變，這不僅會對其飛行特性產生很大的影響，也會對其沖擊破壞效應有所影響。基于前文建立且驗證后的風致飛擲物沖擊浮法玻璃的有限元模型，本章將沖擊物由鋼球換成鋼板，研究板狀飛擲物的沖擊位置、沖擊姿態和外形特性對其沖擊效應的影響。

2.1 沖擊位置

現實中風致飛擲物沖擊建筑玻璃圍護結構的落點是隨機分布的，不同的沖擊落點可能對最終的破壞結果有影響。為了研究浮法玻璃面板在不同位置處抗沖擊性能的差異，本節建立了不同落點的板狀飛擲物沖擊玻璃模型。根據對稱性，選擇邊長為200 mm的正方形浮法玻璃面板上的三個點作為典型的沖擊位置，分別代表中心、邊部和角部位置，如圖4所示。

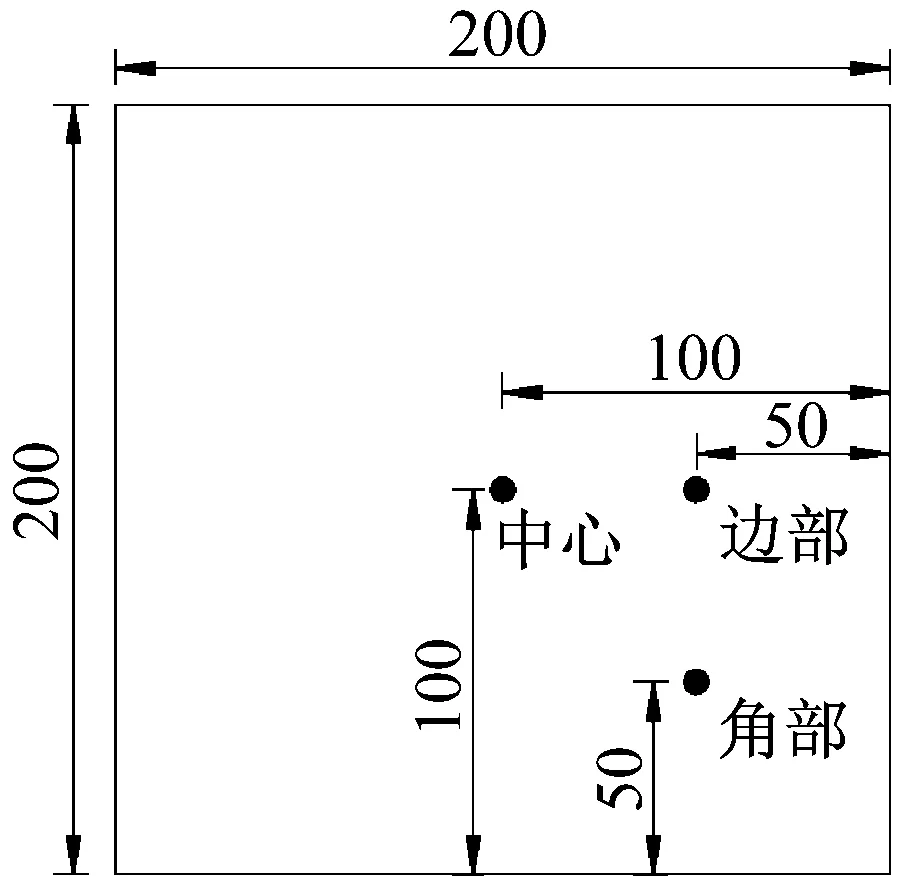
圖4 浮法玻璃面板受沖擊位置示意圖Fig.4 Diagram of the position of float glass panel subjected to the debris impact

在建立板狀飛擲物沖擊玻璃的數值模型時，除了落點位置不同，板狀飛擲物的外形和沖擊姿態等其他變量應保持一致。本文采用的板狀飛擲物尺寸為40 mm×40 mm×2 mm，沖擊姿態為板狀飛擲物主面垂直于玻璃面板平面，如圖5所示。

圖5 板狀飛擲物沖擊玻璃面板姿態示意圖Fig.5 Diagram of the impact attitude of plate-like debris on the float glass panel

圖6為沖擊位置分別為中心、邊部和角部時，玻璃面板被板狀飛擲物破壞后的情況。由圖6可見，板狀飛擲物以主面垂直于玻璃面板平面的姿態沖擊玻璃后，玻璃面板的受損區域相對較小，中心和邊部破壞的情況近似，角部可能存在一部分玻璃面板脫落破壞的現象。表4統計了板狀飛擲物沖擊浮法玻璃面板這三個位置的破壞臨界速度。由表4可知，鋼板分別在中心、邊部和角部三個位置沖擊浮法玻璃面板的破壞臨界速度相差很小。因此，浮法玻璃面板不同位置處的抗沖擊性能差異不大，沖擊位置對板狀飛擲物破壞建筑浮法玻璃結果的影響可以忽略。

(a) 中心

(b) 邊部

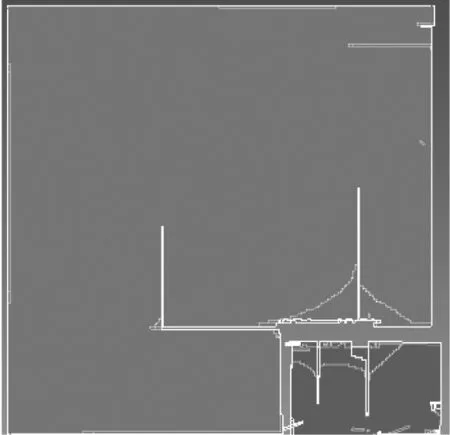
(c) 角部圖6 浮法玻璃面板不同位置受鋼板沖擊后的破壞情況Fig.6 Failures of the float glass panels subjected to the impact of the steel plate at different positions

表4 鋼板沖擊浮法玻璃面板不同位置的破壞臨界速度

2.2 沖擊姿態

在板狀飛擲物沖擊玻璃的瞬間，既可能是其尖角與玻璃先接觸，也可能是棱邊或某一個平面與玻璃先接觸。因此，板狀飛擲物與玻璃面板平面的接觸方式存在“點碰撞”、“線碰撞”和“面碰撞”三種類型，這些接觸方式由板狀飛擲物的沖擊姿態所決定，可能是影響其破壞結果的一個重要因素。在三維空間里，板狀飛擲物的沖擊姿態可以通過X，Y，Z三個坐標軸來確定，本文將板狀飛擲物繞X，Y和Z軸旋轉的角度分別定義為α、β和γ，如圖7所示。

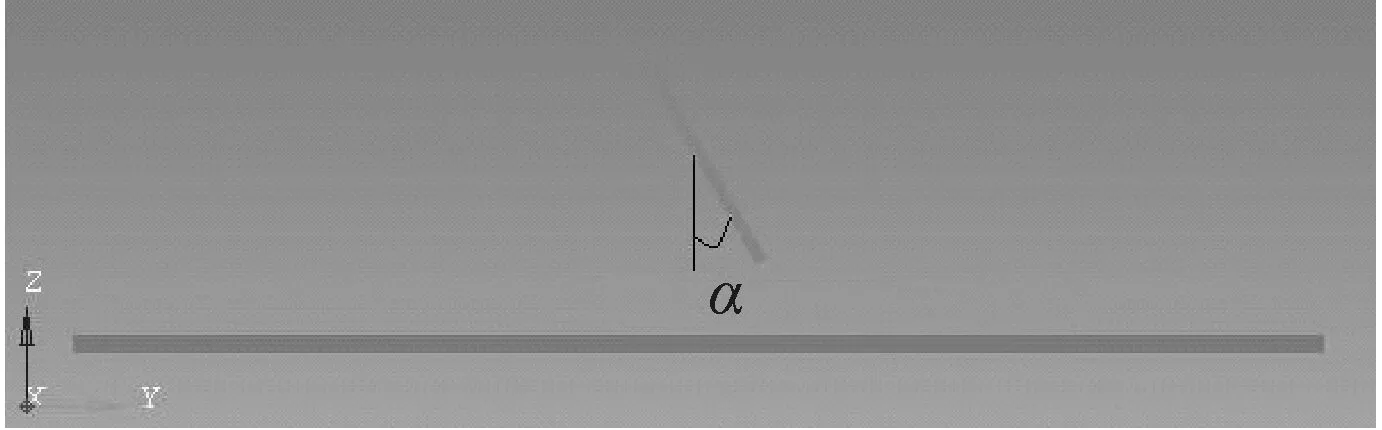
(a) 繞X軸轉角α

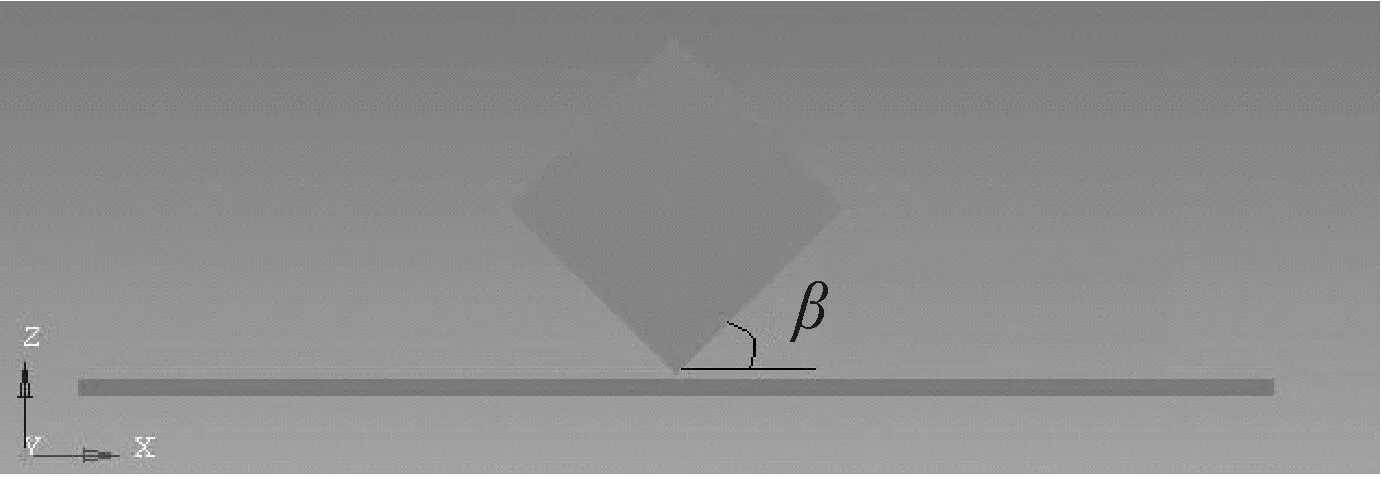
(b) 繞Y軸轉角β

(c) 繞Z軸轉角γ圖7 板狀飛擲物旋轉角度定義Fig.7 Definition of the rotation angle of plate-like debris

由前文可知，板狀飛擲物的沖擊位置對其沖擊效應的影響很小，因此根據對稱性，可不考慮板狀飛擲物繞Z軸旋轉時的沖擊姿態對最終破壞結果的影響，只需考慮板狀飛擲物繞X軸旋轉0°～90°，以及繞Y軸旋轉0°～45°沖擊姿態的影響，即α和β的取值范圍分別為0°～90°和0°～45°。本節以15°為間隔對α和β進行取值，由此得到了28種具有代表性的板狀飛擲物沖擊姿態，并對它們的沖擊過程進行了模擬，將破壞結果匯總為表5。同時，表中還備注了各種沖擊姿態對應的飛擲物和玻璃面板的接觸方式，“P”代表“點碰撞”，“L”代表“線碰撞”，“S”代表“面碰撞”。

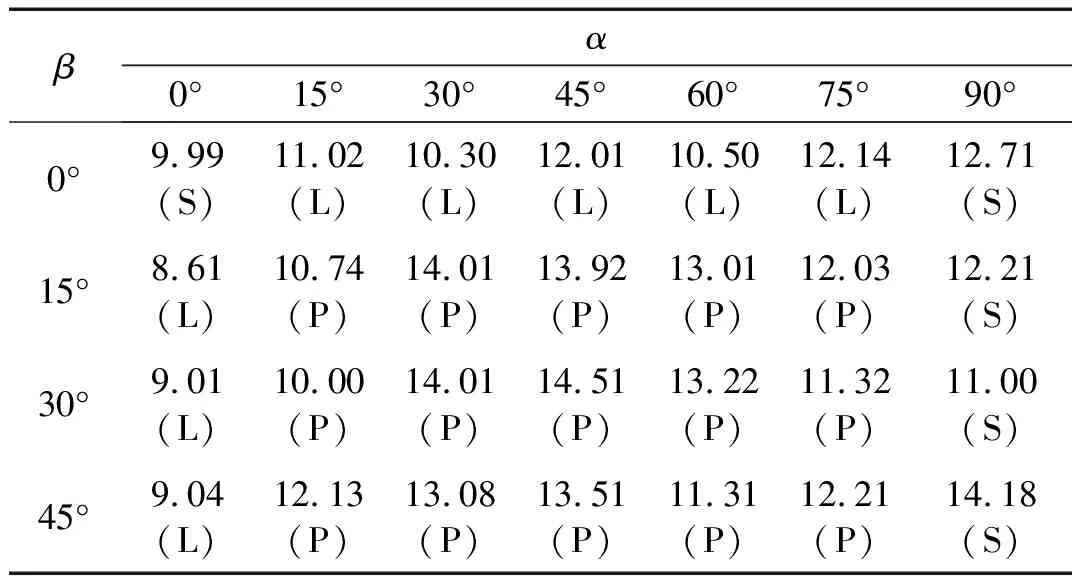
表5 不同沖擊姿態的鋼板沖擊玻璃的破壞臨界速度

由表5可見，板狀飛擲物與浮法玻璃的接觸方式，即“點碰撞”、“線碰撞”和“面碰撞”與飛擲物的破壞臨界速度之間并沒有明顯的聯系。但是當α=0°時，板狀飛擲物的破壞臨界速度普遍較小，均小于10 m/s，即更容易破壞建筑浮法玻璃。而當α>0°時，板狀飛擲物破壞臨界速度普遍較大，均大于10 m/s。為了查明造成這種結果的原因，本文基于數值模擬對全部28種沖擊姿態的板狀飛擲物在破壞玻璃面板過程中姿態的變化進行了觀察與分析。

結果發現，造成α>0°的沖擊姿態破壞臨界速度普遍較大的原因是板狀飛擲物以這些姿態沖擊玻璃時，雖然在飛擲物與玻璃面板接觸瞬間的接觸方式各不相同，但是在隨后的沖擊過程中板狀飛擲物由于受到玻璃面板的阻力將會進一步自由旋轉，從而改變了飛擲物與玻璃面板后續的接觸方式。最后在破壞和能量轉換過程當中，板狀飛擲物都將以“面碰撞”的姿態對玻璃面板進行破壞。而在該種沖擊姿態下，板狀飛擲物與玻璃接觸面積較大，能量耗散更快，故較不容易破壞玻璃面板。

限于篇幅，為了對比板狀飛擲物以不同姿態沖擊后玻璃面板的破壞情況，圖8只列出了飛擲物破壞臨界速度最小(8.61 m/s，α=0°，β=15°)、中等(9.99 m/s，α=0°，β=0°)以及最大(14.51 m/s，α=45°，β=30°)時，玻璃面板的裂紋開展情況。由圖可知，板狀飛擲物的破壞臨界速度越小，玻璃受破壞的區域也越小。因此，對于板狀飛擲物，若其沖擊姿態導致其破壞區域越集中，則越容易破壞建筑玻璃圍護結構。

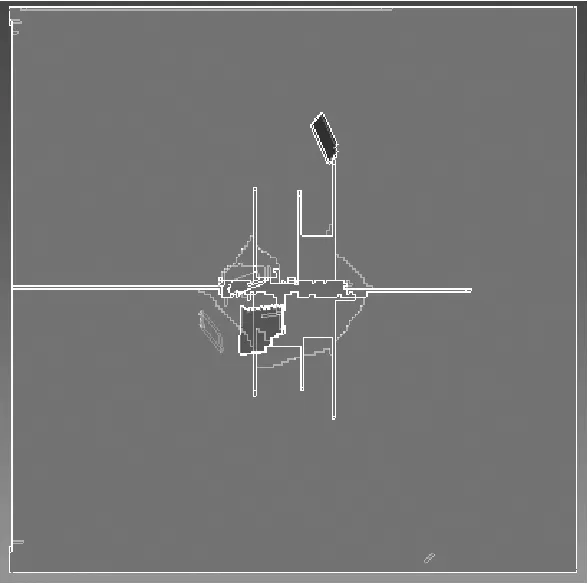
(a) α=0°，β=15°

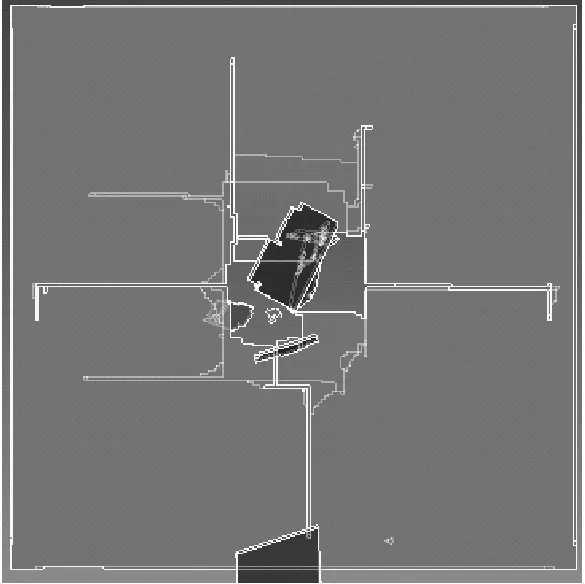
(b) α=0°，β=0°

(c) α=45°，β=30°圖8 鋼板以不同姿態沖擊時，玻璃面板破壞情況對比圖Fig.8 Failures of the float glass panels subjected to the impact of the steel plate with different attitudes

2.3 邊厚比

板狀飛擲物外形較大的差異使其成為風災中飛行軌跡最復雜的一類風致飛擲物，而其對沖擊破壞效應的影響同樣不可忽略。由前文可知，板狀飛擲物的沖擊姿態將會對沖擊效應有所影響，而沖擊位置的影響可以忽略，因此本節在保證飛擲物沖擊姿態相同的情況下，對質量相同，邊厚比不同的板狀飛擲物沖擊效應進行研究。據此，本節共選擇了10∶1、15∶1、20∶1、25∶1和30∶1五種邊厚比的方形板狀飛擲物，對它們沖擊浮法玻璃的過程進行了模擬。板狀飛擲物的質量均為24.96 g，沖擊姿態為α=90°，β=0°，具體尺寸及其破壞臨界速度如表6所示。

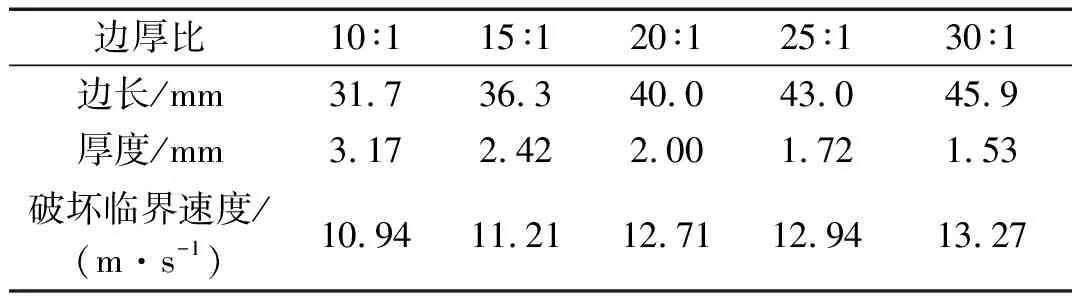
表6 不同邊厚比的鋼板尺寸和破壞臨界速度

由表6可見，以α=90°，β=0°姿態沖擊浮法玻璃時，隨著邊厚比的增大，板狀飛擲物的破壞臨界速度也逐漸增大，即邊厚比越大的板狀飛擲物越不容易破壞玻璃面板。將浮法玻璃面板被這些鋼板以該種姿態沖擊后的破壞情況列出，如圖9所示。由圖可見，邊厚比越大的飛擲物對玻璃面板的破壞區域越大，破壞臨界速度也越大。因此，當板狀飛擲物的質量相同時，邊厚比越小越容易破壞建筑玻璃圍護結構。

(a) 10∶1

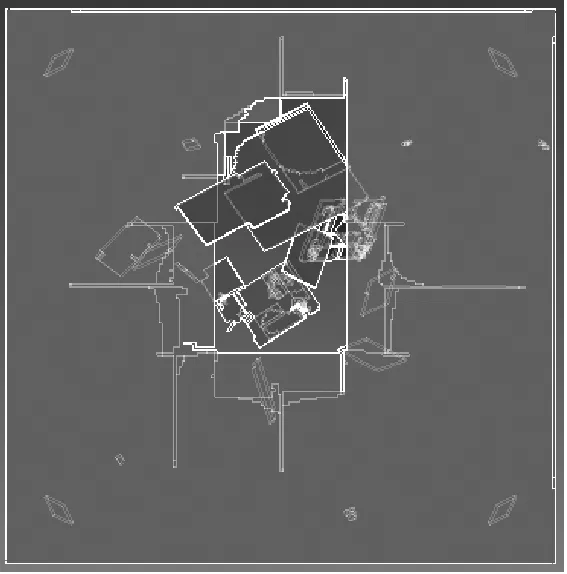
(b) 15∶1

(c) 20∶1

(d) 25∶1

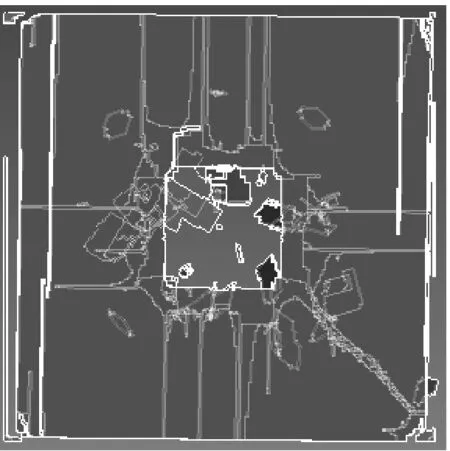
(d) 30∶1圖9 不同邊厚比的鋼板沖擊玻璃面板的破壞情況Fig.9 Failures of the float glass panels subjected to the impact of the steel plate with different ratios of side to thickness

3 結 論

本文通過試驗和數值模擬研究風致飛擲物對建筑浮法玻璃圍護結構的沖擊破壞效應。首先采用鋼球以不同的速度沖擊厚度分別為3 mm和5 mm的浮法玻璃面板進行沖擊破壞試驗，從而得到鋼球的沖擊破壞臨界速度以及浮法玻璃被破壞后的裂紋和碎片飛濺情況。然后基于有限元動力分析軟件LS-DYNA，建立了與試驗相對應的飛擲物沖擊浮法玻璃面板有限元模型，并通過對比試驗和數值模擬的結果，驗證了有限元模型的準確性。最后，以板狀飛擲物為代表，分析了飛擲物的沖擊位置、沖擊姿態和外形等特征對其沖擊破壞效應的影響。主要結論如下：

(1) 沖擊破壞試驗結果表明，直徑40 mm，質量261 g的鋼球破壞3 mm和5 mm厚度浮法玻璃的臨界速度分別僅為4.64 m/s和5.34 m/s。因此，建筑浮法玻璃圍護結構在風災中非常容易受到風致飛擲物的沖擊而遭受破壞。

(2) 在建筑浮法玻璃的有限元數值模擬中，采用JH-2本構模型作為其材料模型，并以75 MPa最大主應力，即SIGP1=75 MPa作為玻璃的失效判斷準則，能夠較準確地模擬浮法玻璃在沖擊荷載作用下的破壞特性。此外，該有限元模型還能夠較準確地模擬浮法玻璃面板被風致飛擲物破壞后的裂紋開展和碎片飛濺情況。因此，本文建立的風致飛擲物沖擊浮法玻璃的有限元模型具有較高的可靠性，可用于對風致飛擲物沖擊特性的進一步研究。

(3) 板狀飛擲物的沖擊位置對其沖擊破壞效應的影響不大，但是板狀飛擲物的沖擊姿態和邊厚比有較大的影響。板狀飛擲物的沖擊姿態為主平面垂直于玻璃面板平面(α=0°)時最容易破壞玻璃面板，但是當板狀飛擲物以與玻璃面板平面接觸面積較大的姿態沖擊時，由于破壞區域大、能量耗散快，故較不容易破壞玻璃面板。此時質量相同但邊厚比不同的板狀飛擲物沖擊結果相差也較大，邊厚比越小的板狀飛擲物越容易破壞玻璃面板。