基于多尺度均值排列熵和參數優化支持向量機的軸承故障診斷

王貢獻, 張 淼, 胡志輝, 向 磊, 趙博琨

(武漢理工大學 物流工程學院，武漢 430063)

滾動軸承是廣泛應用于旋轉機械的易損重要零部件，其運行狀態直接影響機械設備工作效率和安全性[1]。因此，對滾動軸承運行狀態進行監測與診斷，尤其是滾動軸承早期故障診斷具有重要意義[2]。

由于滾動軸承自身非線性剛度和軸承間隙等因素，其運行產生的振動信號經常表現出非平穩和非線性[3]。因此，實現從非平穩和非線性信號中提取有用故障特征信息是滾動軸承故障診斷的重點和難點。基于熵的方法可以識別非線性參數，如近似熵[4]、排列熵[5]、模糊熵[6]和多尺度熵[7]，其中，Christoph等[8]提出的排列熵(permutation entropy, PE)無需考慮時間序列的數值大小，而是對相鄰樣本點進行對比分析，獲取相應特征信息，用于檢測時間序列隨機性和動力學突變，具有計算簡單、抗噪能力強和計算速度快等優點，故被廣泛用于故障診斷[9]。PE與信號處理方法結合能夠提取時間序列特征信息，如局部特征尺度分解[10]、集合經驗模態分解[11]和變分模態分解[12]。然而，PE算法僅考慮單一尺度下時間序列數據信息，特征提取能力不足。為此，Aziz等[13]結合PE與多尺度熵提出了多尺度排列熵(multiscale permutation entropy, MPE)。鄭近德等[14]將MPE與SVM結合用于滾動軸承故障診斷，取得較高的故障識別準確率，證明了MPE能夠有效提取時間序列特征信息。然而，MPE仍存在以下缺陷，一方面，對時間序列粗粒化處理會導致粗粒化序列長度變短，當粗粒化尺度較大時不可避免地容易丟失原始信息，并且熵值的估計偏差會隨著尺度增大而增大；另一方面，粗粒化過程將一個時間序列分割為等長的非重疊的片段再計算每一個片段內所有數據點的均值，這種均值化處理會一定程度上中和原始信號的動力學突變行為。

在充分提取振動信號故障特征信息基礎上，滾動軸承故障診斷的關鍵是利用特征信息實現故障模式識別。支持向量機(support vector machine, SVM)在小樣本、低維度數據分類上具有速度快、準確率高的優點，故被廣泛用于故障診斷領域，然而SVM性能容易受到懲罰因子c和核函數參數g影響。為此，有學者將網格尋優算法[15]、遺傳算法[16]、粒子群優化算法[17]和模擬退火算法[18]等用于SVM參數尋優，但這些方法存在尋優耗時長和容易陷入局部最優解等問題。灰狼算法[19](grey wolf optimization，GWO)具有參數簡單、全局搜索能力強、收斂速度快和易于實現等優點，將其用于SVM超參數選擇，可以提高分類精度。宋宣毅等[20]利用GWO-SVM實現了油井初期產能預測。Dong等[21]將時移多尺度加權排列熵與GWO-SVM結合用于軸承故障診斷。上述方法均具有較好的實用性。

針對MPE的不足，將多尺度均值化代替粗粒化方法，提出了一種多尺度均值排列熵算法(multiscale mean permutation entropy, MMPE)，旨在更加充分提取時間序列有用特征信息。在此基礎上，采用GWO-SVM多分類器進行故障模式識別，并建立一種基于MMPE和GWO-SVM的滾動軸承故障診斷模型，通過提取原始時間序列的MMPE特征信息構成特征數據集，用訓練集訓練GWO-SVM，在測試集進行故障模式識別，將其應用于滾動軸承試驗數據，可為滾動軸承故障診斷提供理論參考。

1 多尺度均值排列熵

1.1 多尺度排列熵

MPE考慮多個尺度下時間序列順序結構特征，能夠充分提取信號特征信息，具體算法如下：

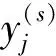
(1)

式中:[N/s]為對N/s取整數;s為正整數尺度因子。當s=1時，粗粒化序列即為原始序列；當s=2,3,…時，原始系列變為長度為[N/s]的粗粒化序列。

分別計算尺度1～s的粗粒化序列PE值，構成原始序列s尺度MPE。

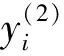
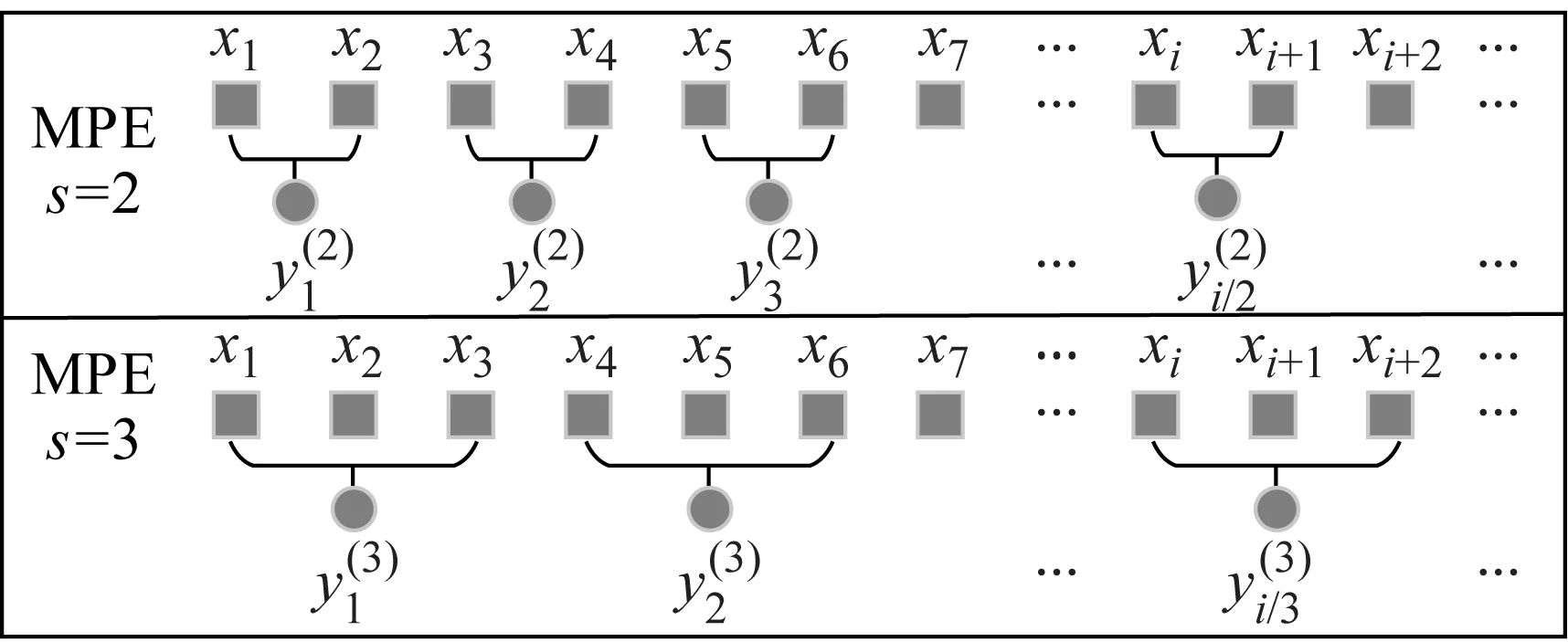
圖1 MPE粗粒化構造方式(s=2和3)Fig.1 Coarse grained structure of MPE(s=2 and 3)

1.2 多尺度均值排列熵

針對MPE存在的不足，同時考慮到對相同連續信號進行離散采樣，不同采樣頻率和采樣起點所得時間序列不同，造成其PE值不同。為此，提出多尺度均值排列熵(multiscale mean permutation entropy, MMPE)，旨在保留更多的數據信息、減少信號采樣誤差和擴充樣本，具體算法原理如下：

(2)

當s=1時，均值化序列即為原始序列；當s=2,3,…時，原始序列變為長度為(N+1-s)的均值化序列。

分別計算尺度1到s的均值化序列PE值，構成原始序列s尺度MMPE。

MMPE時間序列均值化方式如圖2所示，其實質是在時間序列上加寬度為s、步長為1的滑動窗口，每個窗口內部取均值得到均值化序列，均值化過程除首尾幾個點外，每個數據點重復使用s次，充分提取原始數據信息。以s=3為例，長度為N的時間序列x(i)進行均值化處理后得到長度為(N-2)的新序列，計算尺度1、2和3均值化序列排列熵值PE1、PE2和PE3，構成的3維向量即時間序列3尺度MMPE。

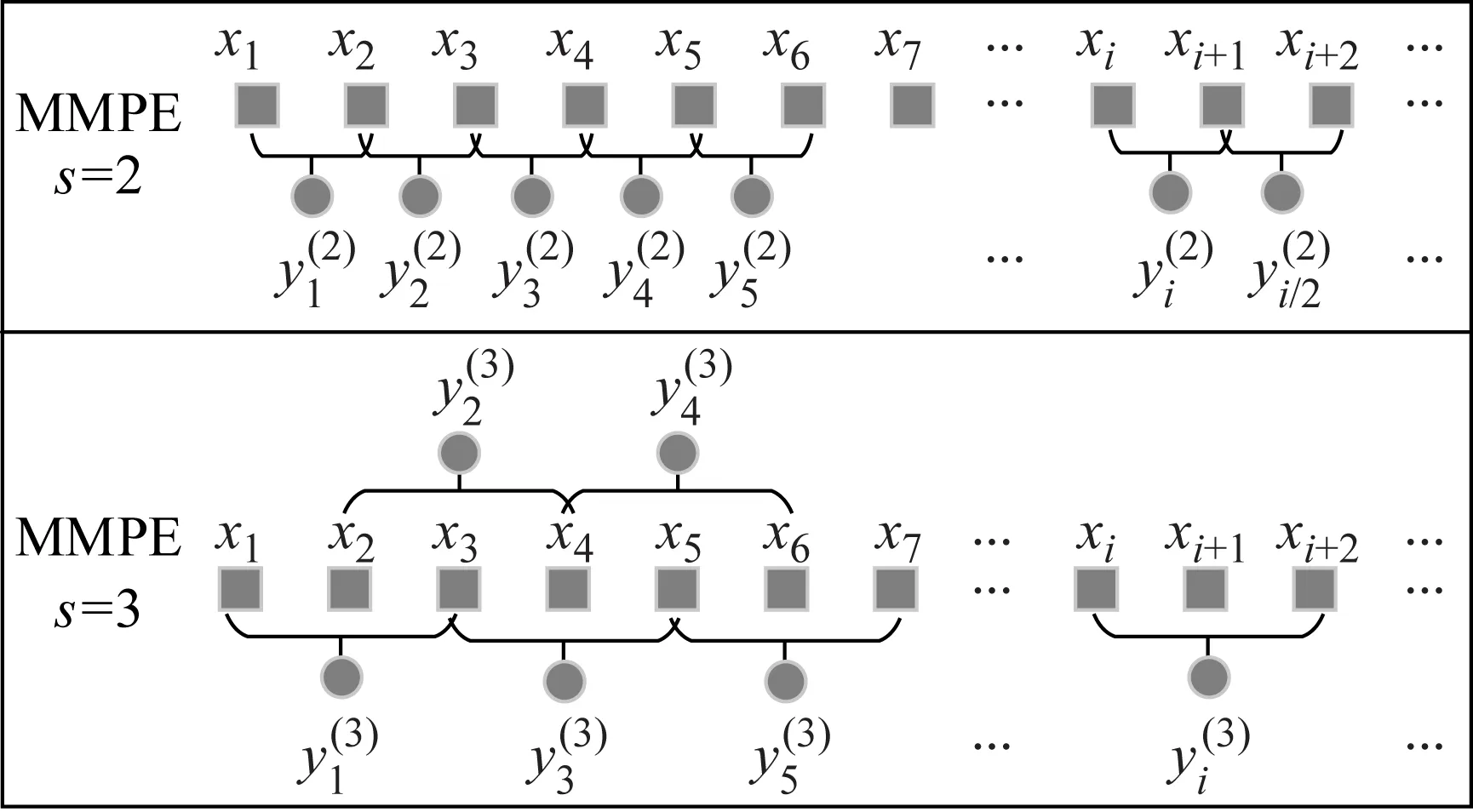
圖2 MMPE均值化構造方式(s=2和3)Fig.2 The mean structure of MMPE(s=2 and 3)

2 灰狼優化支持向量機

2.1 灰狼算法

灰狼算法(grey wolf optimization, GWO)是一種模擬狼群等級制度和分工狩獵行為的新型群體智能優化算法。GWO中狼群根據社會等級依次記為頭狼α、β狼、σ狼和ω狼。捕獵過程中將每只狼作為潛在捕獵方案，α、β和σ依次作為第一、第二和第三最優解，狼群根據獵物信息不斷調整移動，狩獵過程包括：追蹤、包圍和攻擊獵物。

(1) 追蹤和包圍獵物，狼群根據與獵物間的距離不斷調整自身位置，其數學描述如下

D=|CXp(t)-X(t)|

(3)

X(t+1)=Xp(t)-AD

(4)

式中:D是灰狼與獵物間距離;Xp(t)為獵物當前位置；t為迭代次數；X(t)為灰狼當前位置；A和C是系數矩陣。A和C可表示如下

A=2ar1-a

(5)

C=2ar2

(6)

當|A|>1時，狼群將擴大搜索范圍，以尋找更好的獵物。相反，當|A|≤1時，狼群將縮小包圍圈并搜尋附近的獵物。r1，r2為[0,1]間隨機值；a為收斂因子，隨著迭代次數增加從2線性遞減到0。

(2) 靠攏并攻擊獵物，狼群尋找到獵物大致方位后，將靠攏并對獵物發起攻擊，這種行為數學描述為

(7)

(8)

X(t+1)=(X1+X2+X3)/3

(9)

式中:Xα(t)、Xβ(t)、Xσ(t)分別為α、β和σ的當前位置；Dα、Dβ和Dσ分別為α、β和σ與獵物之間的距離；X1、X2和X3代表α、β和σ指導ω下一步移動的方向向量，狼群下一步移動的方向向量由式(9)決定。

2.2 灰狼優化支持向量機

支持向量機(SVM)因其優異的分類性能和可靠性被廣泛用于故障診斷領域，然而SVM性能易受懲罰因子c和核函數參數g的影響。GWO具有參數簡單、全局搜索能力強、收斂速度快和易于實現等優點，將其用于SVM超參數選擇，可以提高分類精度。GWO-SVM流程如圖3所示，具體過程如下：

步驟1 輸入訓練數據和測試數據，初始化GWO參數，設定種群規模p、最大迭代次數t0和搜索空間維度T，在設定范圍內隨機生成狼群位置。

步驟2 初始化SVM參數，設置c和g的搜索范圍，以SVM識別準確率作為適應度函數。

步驟3 計算當前位置狼群的適應度函數值，通過式(7)和(8)不斷更新狼群位置和適應度函數值。

步驟4 判斷迭代次數，當迭代次數不超過設定最大值時返回步驟3，否則，尋優結束，輸出最佳參數c和g。

步驟5 使用最佳參數c和g開始訓練SVM，用訓練好的模型在測試集上進行故障分類。

圖3 GWO-SVM流程圖Fig.3 The flowchart of GWO-SVM

3 故障診斷模型

為實現滾動軸承故障診斷，在得到原始振動信號MMPE并構成特征數據集后，采用GWO-SVM多分類器進行故障模式識別。基于MMPE和GWO-SVM的故障診斷方法流程如圖4所示，具體步驟如下：

步驟1 假定滾動軸承有k種狀態類型，每種類型采集i組樣本，根據信號數據分析確定MMPE參數，包括樣本長度N、嵌入維數m、尺度因子s和時延λ。

步驟2 計算每個樣本MMPE值作為輸入特征向量。

步驟3 將MMPE計算結果匯總，根據故障類型設置1～k標簽，每種類型選取j個樣本作為訓練樣本，剩余樣本作為測試樣本，分別構成訓練樣本特征集和測試樣本特征集。

步驟4 采用訓練樣本特征集對GWO-SVM多分類器進行訓練，灰狼算法自動選取最佳參數c和g。

步驟5 用訓練好的GWO-SVM多分類器對測試樣本特征集進行故障類型和故障程度識別。

圖4 故障診斷模型流程圖Fig.4 The flowchart of fault diagnosis model

4 滾動軸承故障診斷試驗研究

4.1 試驗數據

為驗證MMPE和GWO-SVM方法對軸承故障診斷的有效性，將其應用于凱斯西儲大學軸承數據進行試驗分析。試驗采用6205-2RS型深溝球軸承，利用電火花技術分別在軸承外圈、內圈和滾動體上進行單點故障加工，故障直徑分別為0.177 8 mm、0.355 6 mm和0.533 4 mm，故障深度為0.279 4 mm，電機載荷為3馬力，試驗電機轉速為1 730 r/min，在12 kHz采樣頻率下采集到正常(normal, NOR)，外圈故障(outer race fault, ORF)，內圈故障(inner race fault, IRF)和滾動體故障(ball fault, BF)四種狀態的振動信號。

為進行故障位置和故障程度識別試驗，將每種故障軸承信號按故障直徑大小分為輕微、中度和嚴重三種故障程度，總計得到10種狀態的信號(對應標簽為1～10)，分別記為正常NOR、內圈輕微故障IRF1、外圈輕微故障ORF1、滾動體輕微故障BF1、內圈中度故障IRF2、外圈中度故障ORF2、滾動體中度故障BF2、內圈嚴重故障IRF3、外圈嚴重故障ORF3、滾動體嚴重故障BF3，每種狀態取50個樣本，每個樣本含2048個數據點。各種狀態的軸承信號數據信息如表1所示，其時域波形如圖5所示。

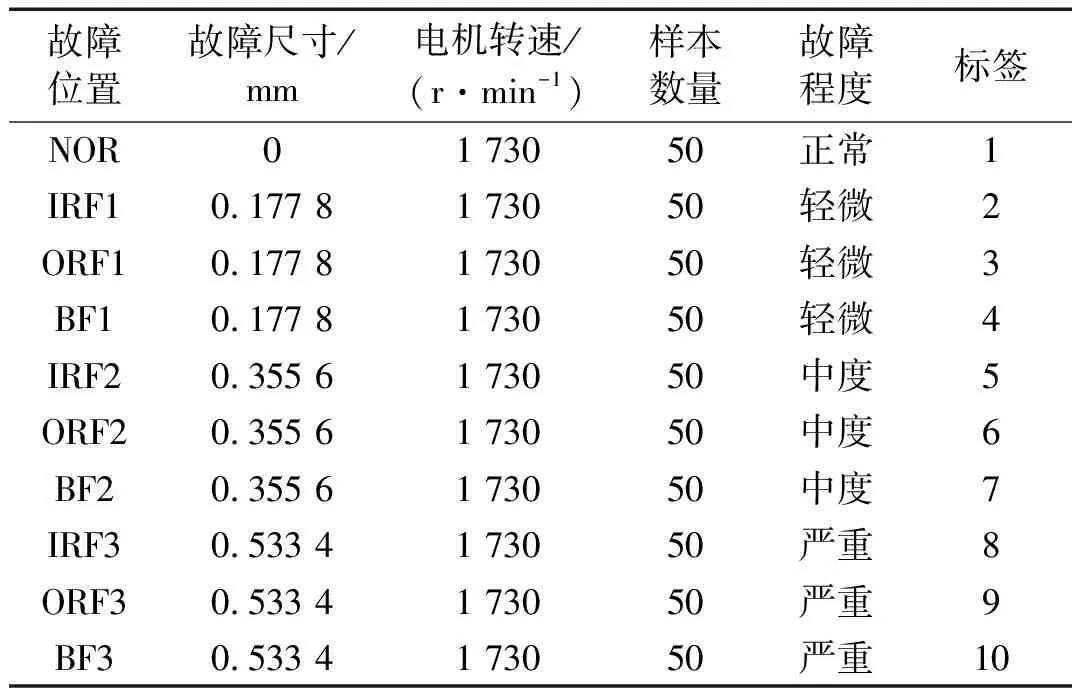
表1 軸承數據信息

圖5 軸承信號時域波形Fig.5 Time domain waveforms of bearing signal

4.2 MMPE參數選擇和分析

MMPE具有4個關鍵參數，分別為樣本長度N、尺度因子s、時延λ和嵌入維數m。MMPE算法基本不會改變數據長度，因此對N取值不敏感，而MPE的粗粒化處理時，s越大則需要N越大；s取值沒有固定要求，一般s大于10即可。為對比MMPE與MPE的特征提取能力，參照文獻[14]中MPE參數取值，N、s分別設置為2 048和12。λ對熵值影響較小，一般設定為1。m的選擇對MPE和MMPE具有較大影響，m過小，相空間重構向量信息不足，無法有效監測序列動力學突變；反之，m過大，相空間重構向量忽略序列細微變化，并且會增加運算時間，通常m的取值4～7之間。

為探究嵌入維數m對時間序列MMPE的影響，分別從NOR、IRF、ORF和BF信號中隨機選取一組樣本數據，m分別設置為4、5、6、7，計算其MMPE。四組樣本信號MMPE結果如圖6所示。

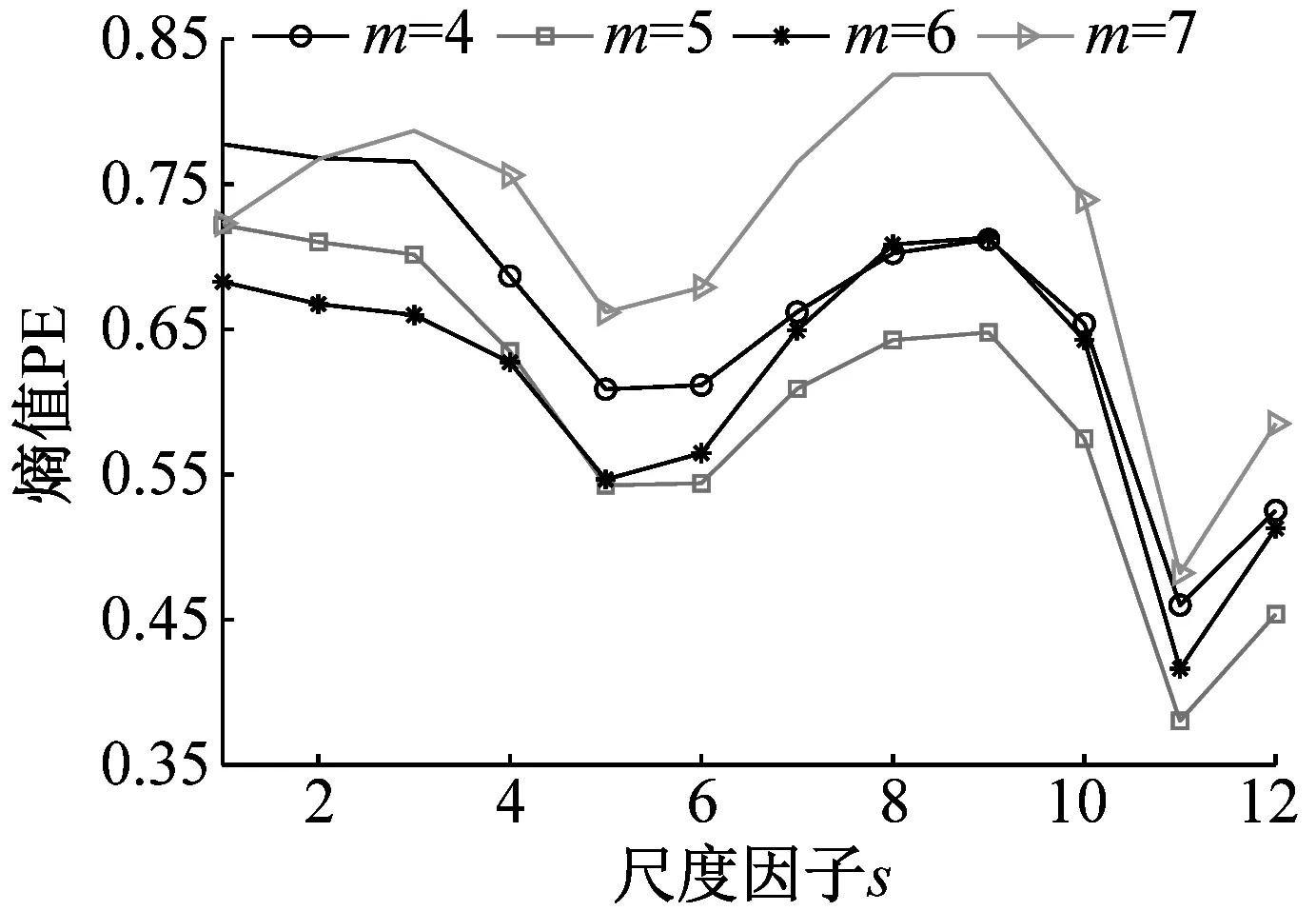
(a) 正常信號

(b) 內圈故障信號

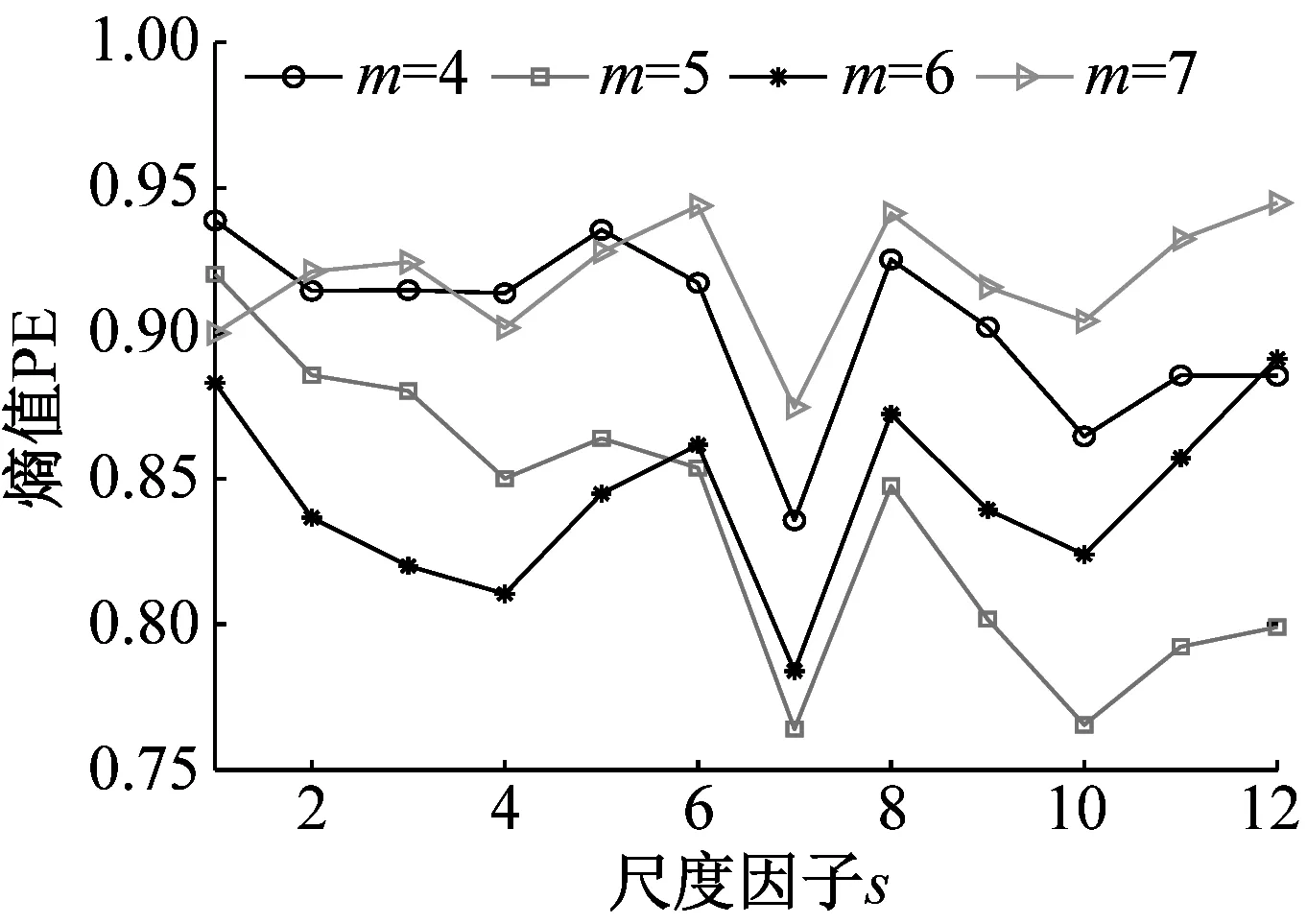
(c) 外圈故障信號

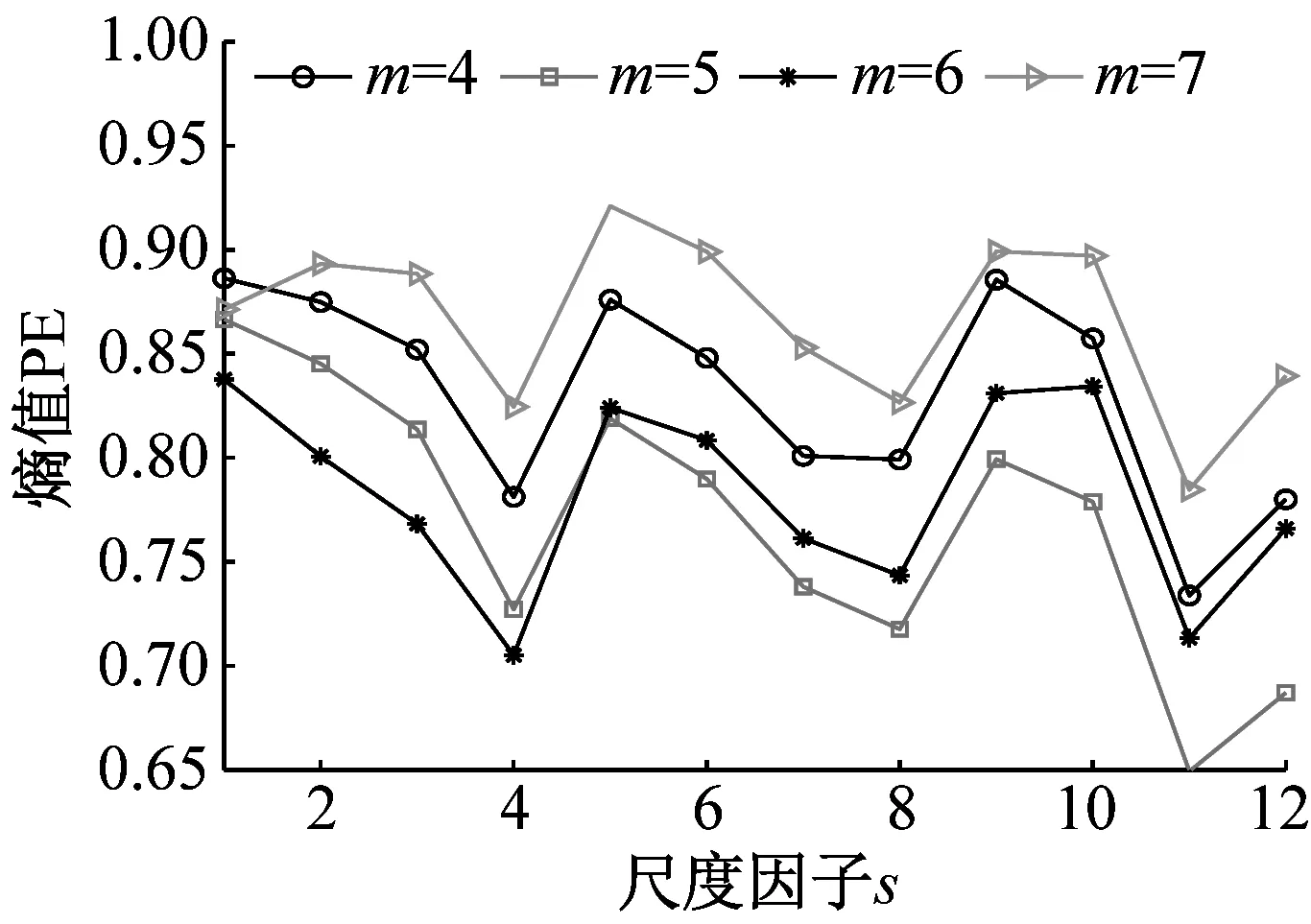
(d) 滾動體故障信號圖6 不同m下，MMPE對不同信號分析結果Fig.6 Analysis results of different signals by MMPE with different m

分析圖6可知:(1)當s小于4時，PE值隨著s增加而減小，表明了在s較小時均值化處理能使時間序列更加平穩規則；當s大于4時，PE值沒有明顯的規律性，不能表征軸承狀態，并且SVM適合處理低維數據，因此選取前4個尺度的熵值作為特征向量，即T=(PE1，PE2，PE3，PE4);(2)當m=6時，四種狀態軸承信號前4個尺度的PE值較小，其MMPE能夠更好的表征信號狀態信息，因此試驗時m設置為6。

10種軸承狀態各隨機選取一組數據，其MMPE如圖7所示，正常狀態軸承信號排列熵較小，其前四個尺度PE值均小于0.7，符合正常狀態軸承信號沖擊性小、平穩性高的振動特性；各故障信號的MMPE均較大，并且對于同種故障，故障尺寸不同其排列熵值也明顯不同，表明MMPE理論上能夠表征軸承振動信號狀態信息，可作為模式識別分類器的輸入。

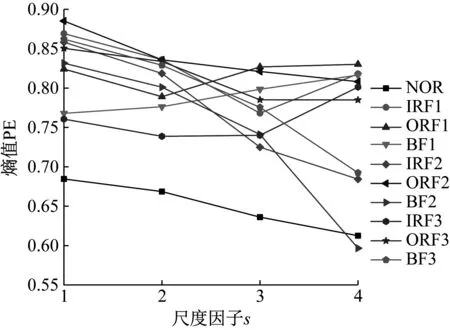
圖7 不同狀態軸承信號的MMPEFig.7 MMPE of bearing signals in different states

4.3 參數優化SVM試驗研究

從每種軸承狀態數據50組樣本中各選取30組作為訓練集，剩余20組作為測試集，構成300×5的訓練數據集和200×5的測試數據集，數據集的前4維是信號前4個尺度的PE特征值，最后1維為標簽。GWO參數設置：狼群數量為10，最大迭代次數為100，懲罰因子c取值范圍[0.01,100]，核函數參數g取值范圍[0.01,100]。SVM核函數選擇徑向基函數，利用MMPE訓練集訓練GWO-SVM，并在測試集上進行驗證。

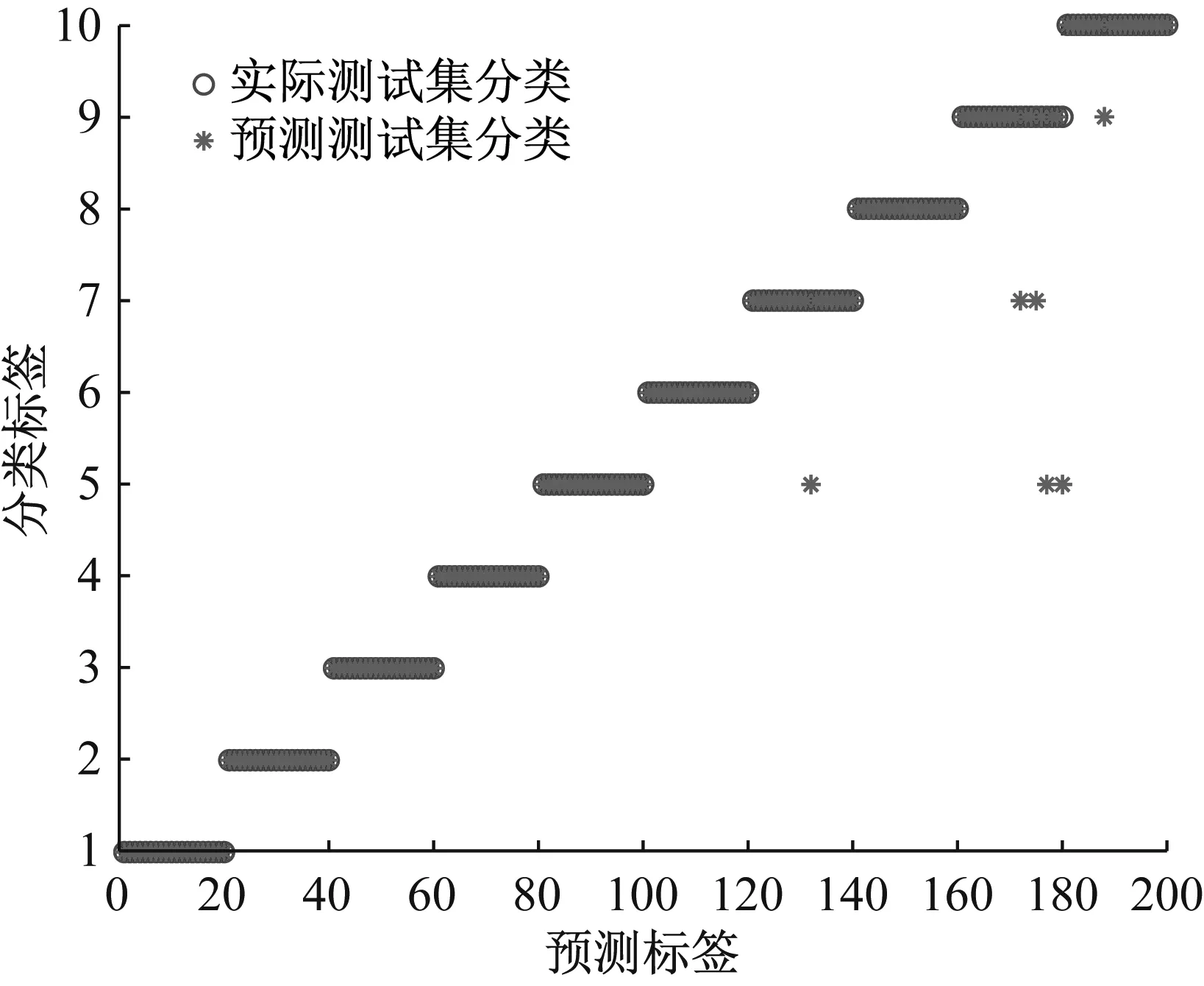
基于MMPE和GWO-SVM的滾動軸承故障診斷結果如圖8所示，前8種狀態軸承測試樣本分類準確率為100%；外圈嚴重故障的20個測試樣本中2個樣本被誤判為內圈中度故障；滾動體嚴重故障的20個測試樣本中1個被誤判為內圈中度故障，1個被誤判為滾動體中度故障。測試集整體識別準確率為98.0%(196/200)。

為了驗證GWO-SVM分類器的優越性，將GWO-SVM其他常用優化支持向量機(GS+SVM、GA+SVM、PSO+SVM和SA+SVM)進行試驗對比，每種分類器進行五次試驗，分別記錄故障識別準確率(acc)和訓練用時(t)，各分類器的對參數c和g的尋優范圍均為[0.01,100]，其他參數設置如表2所示。

表3為GA-SVM、GA-SVM、PSO-SVM、SA-SVM和GWO-SVM分類結果，對比可知：①MMPE與各種參數優化SVM結合的方法在滾動軸承故障診斷中均取得較高的分類準確率，最低為96.5%。②GS-SVM尋優時間短，但分類準確率(96.5%)較低；GA-SVM訓練用時較長，平均分類準確率為97.3%，但每次試驗分類準確率不同，表明該方法對初始化參數較為敏感；PSO-SVM，SA-SVM和GWO-SVM三種分類器準確率都為98.0%，但PSO-SVM尋優時間為59.3 s，SA-SVM尋優時間為10.2 s，而GWO-SVM只需要4.6 s即可完成尋優。因此，GWO-SVM在尋優時間和識別準確率上都優于其他方法。

(a) MMPE+GWO-SVM識別結果

(b) MMPE+GWO-SVM混淆矩陣圖8 MMPE+GWO-SVM識別結果和混淆矩陣Fig.8 Recognition results and confusion matrix of MMPE+ GWO-SVM

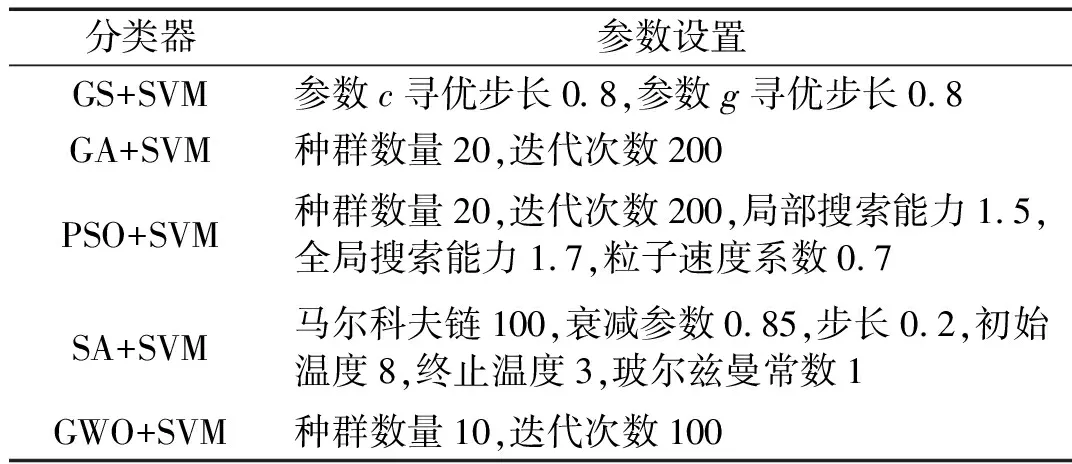
表2 SVM分類器參數Tab.2 Parameters of SVM classifier

4.4 MMPE與MPE特征提取性能對比

為對比分析MMPE和MPE特征提取性能，進行MPE和GWO-SVM軸承故障診斷試驗，各參數設置與MMPE和GWO-SVM試驗一致。利用MPE訓練集訓練GWO-SVM，并在測試集上進行驗證。

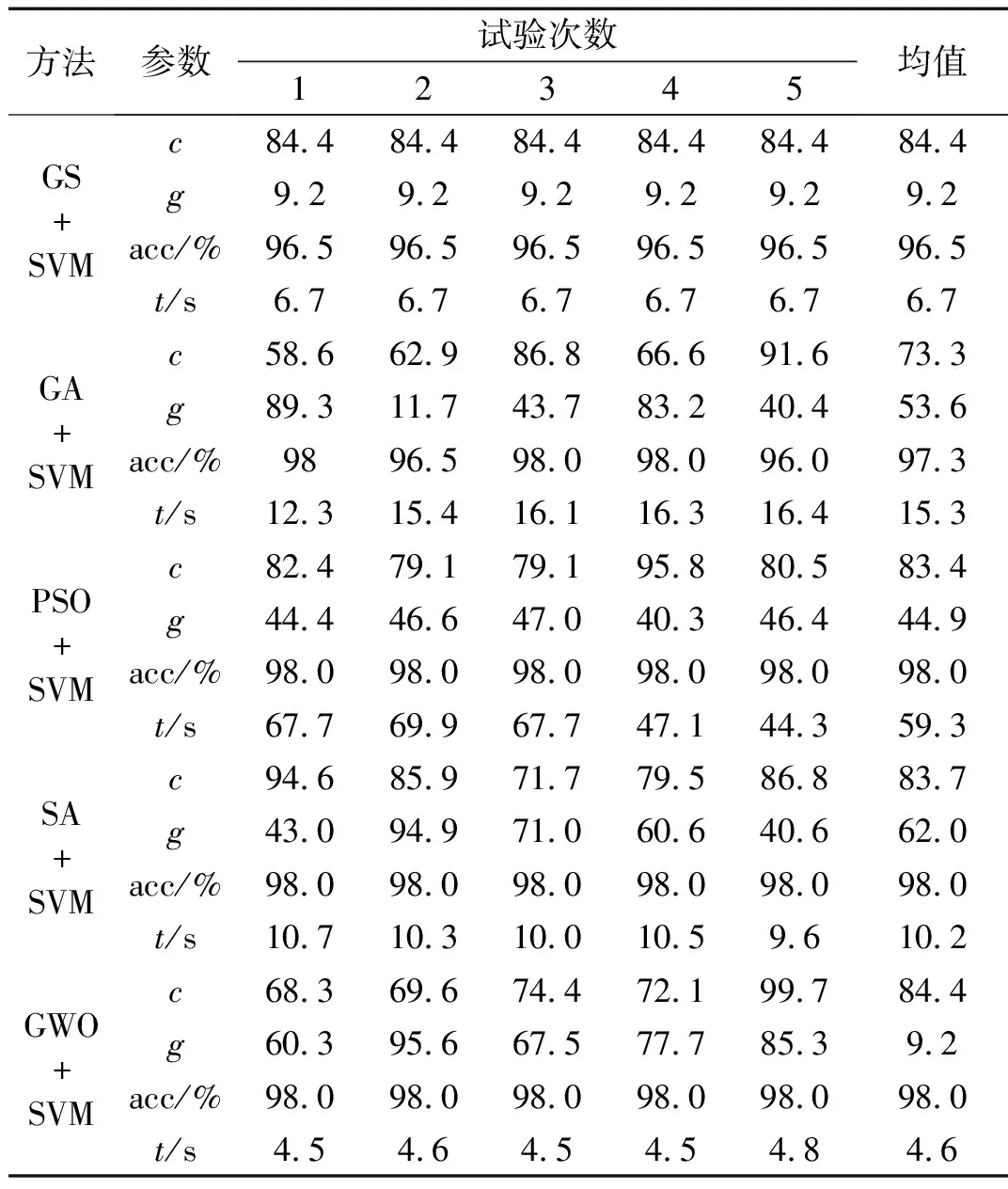
表3 不同分類器識別結果

基于MPE和GWO-SVM的滾動軸承故障診斷結果如圖9所示，前6種狀態和第8種狀態軸承測試樣本分類準確率為100%；滾動體中度故障的20個測試樣本中1個樣本被誤判為內圈中度故障；外圈嚴重故障的20個測試樣本中2個被誤判為內圈中度故障，2個被誤判為滾動體中度故障；滾動體嚴重故障的20個測試樣本中1個樣本被誤判為內圈嚴重故障。測試集整體識別準確率為97.0%(194/200)，低于本文所提出的MMPE和GWO-SVM方法。

為探究MMPE特征提取的噪聲魯棒性，進行噪聲背景下的滾動軸承故障診斷試驗。向各組軸承數據添加性噪比為20 dB的高斯白噪聲，分別計算其MMPE和MPE，輸出數據分別構成MMPE數據集和MPE數據集(試驗分組和試驗參數與前述試驗相同)，并建立相同的GWO-SVM模型，分別用兩個數據集進行模型訓練，通過各自的測試集進行模型評估。

噪聲背景下滾動軸承診斷結果如圖10所示，加入相同白噪聲后，基于MPPE和GWO-SVM方法識別準確率為93.5%(187/200)，而基于MPE的GWO-SVM方法識別準確率僅為83.0%(166/200)，表明了MMPE和GWO-SVM方法具有更好的噪聲魯棒性。

(a) MPE+GWO-SVM識別結果

(b) MPE+GWO-SVM混淆矩陣圖9 MMPE+GWO-SVM識別結果和混淆矩陣Fig.9 Recognition results and confusion matrix of MPE+GWO-SVM

(a) 噪聲背景下MMPE+GWO-SVM識別結果

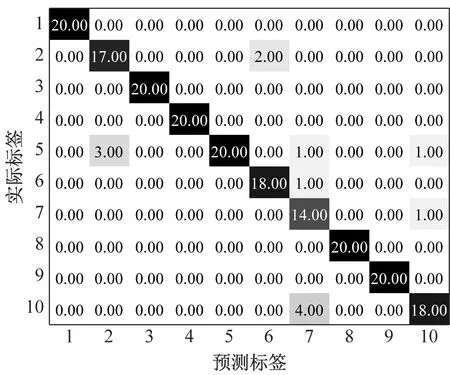
(b) 噪聲背景下MMPE+GWO-SVM混淆矩陣

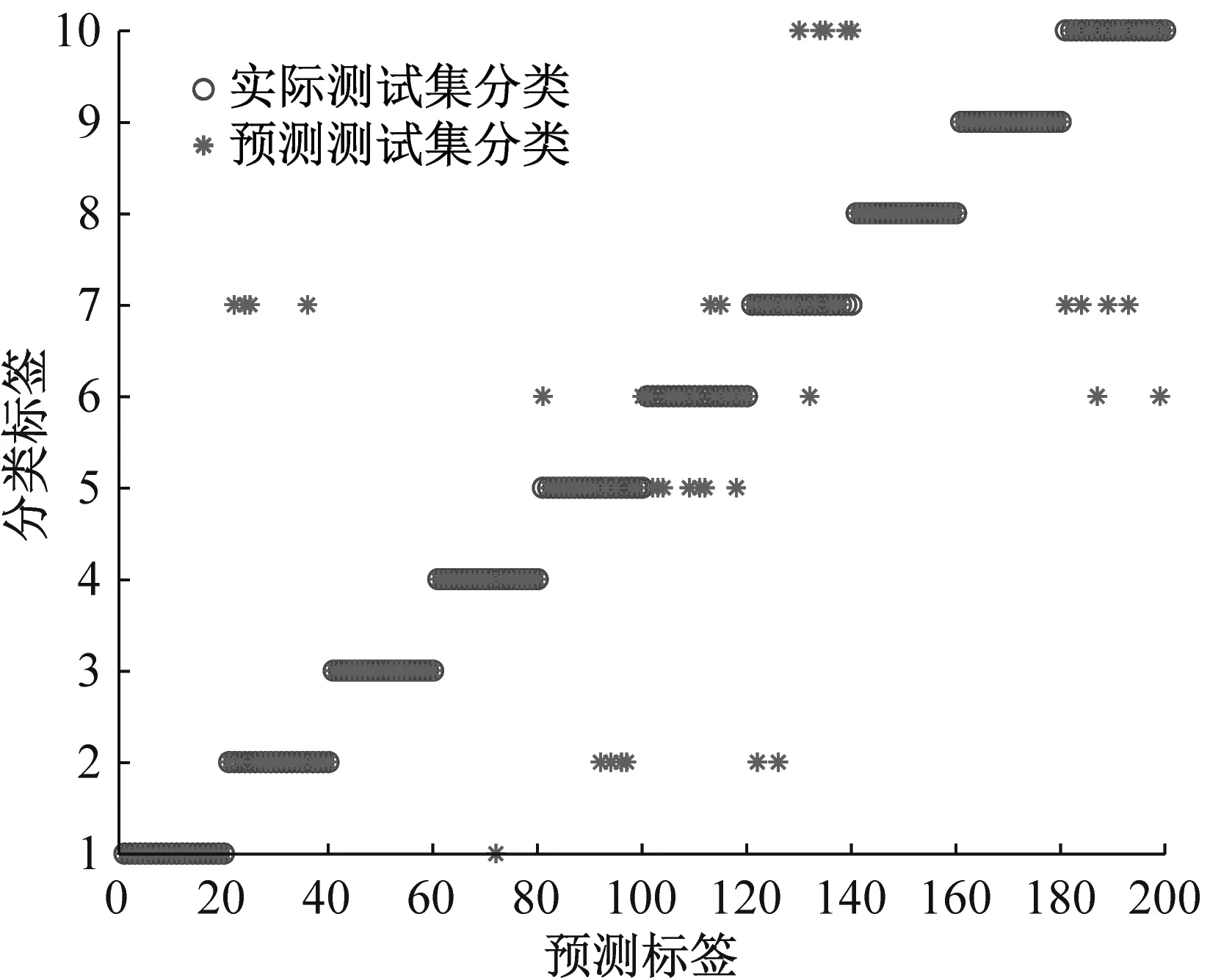
(c) 噪聲背景下MPE+GWO-SVM識別結果

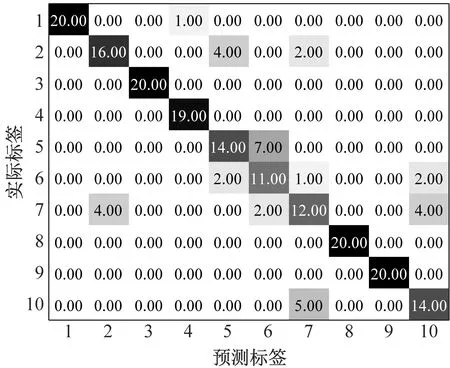
(d) 噪聲背景下MPE+GWO-SVM混淆矩陣圖10 噪聲背景下識別結果和混淆矩陣Fig.10 Recognition results and confusion matrix in noise background

5 結 論

(1) 提出了一種衡量時間序列復雜性的新算法——多尺度均值排列熵MMPE，該算法對原始時間序列進行多尺度均值化處理后計算排列熵，可用于信號特征提取。

(2) 提出了一種基于MMPE和GWO-SVM結合的模式識別方法，滾動軸承故障診斷試驗結果表明，GWO-SVM分類器識別準確率和識別速度均優于常用的GS-SVM、GA-SVM、PSO-SVM和SA-SVM。

(3) MMPE和GWO-SVM方法在軸承故障診斷試驗上取得98%識別準確率，高于MPE和GWO-SVM方法97%準確率。噪聲背景下MMPE和GWO-SVM方法取得93.5%識別準確率，高于MPE和GWO-SVM方法83%準確率，表明MMPE特征提取具有更好的噪聲魯棒性。