質量偏心Timoshenko梁的振動波特性研究

王 劍, 袁秀峰, 胡永彪

(1.長安大學 工程機械學院,西安 710064;2.法蘭泰克重工股份有限公司,江蘇 蘇州 215211)

工程實踐中，梁模型是船體低頻段動力學分析最常用的簡化物理模型[1-2]。

Fahy[7]在其著作中分析了桿的縱向振動波、Timoshenko梁的彎曲波，發現桿中的縱向波為非頻散的傳播波，梁中的彎曲波一組為衰減波，一組為傳播波。El Masri等[8]指出梁中的衰減波在截止頻率之后會轉變為傳播波。有大量學者對于振動波在梁結構中的傳播，進行了詳細研究，比如在漸變截面梁[9]、曲梁[10]、含有非線性間斷梁[11]中的傳播，軸向力對彎曲波的影響[12]。Mei[13]詳細分析了Timoshenko梁中彎曲波的傳播特性，為利用行波法研究非連續復雜梁結構的動力學特性打下基礎。Kalkowski等[14]用實驗測量了變截面梁中的彎曲與縱向波數。

本文針對質量偏心Timoshenko梁，首先推導了其截止頻率的解析表達式；考察了質量偏心下三組振動波的變化，尤其是波型轉變效應；分辨了三組波數對應的振動形式，并研究了質量偏心及頻率變化對各組波數對應位移比的影響。

1 公式推導

考慮質量偏心的Timoshenko梁彎-縱耦合振動方程如式(1)和(2)

(1)

(2)

式中:ρ是梁的密度;A是梁的截面面積;e是質量中心和形心之間的距離;I是梁截面的截面慣性矩；u是梁的縱向位移;v是梁的橫向位移；E是彈性模量;k是截面的剪切系數;G是剪切模量。

采用分離變量法

u(x,t)=U(x)sin(ωt+φ)=Beλxsin(ωt+φ)

v(x,t)=V(x)sin(ωt+φ)=Ceλxsin(ωt+φ)

(3)

(4)

其中：

Z11=ρ2eω4+ρekGω2λ2

Z12=kGEλ3+kGρω2λ

Z22=ρAekGω2λ

式(4)有非零解，其系數矩陣的行列式為零可得到特征方程

E2kGI·S3+Eρω2(EI+2kGI+2kGAe2)·S2+

ρω2(2EIρω2+2EAe2ρω2+kGρIω2+

kGρAe2ω2-kGEA)·S+

ρ2ω4[(I+Ae2)ρω2-kGA]=0

(5)

其中,S=λ2。

式(5)為關于S的一元三次方程，將其改寫為

aS3+bS2+cS+d=0

(6)

根據卡爾丹求根理論[15]，其三個根分別為

(7)

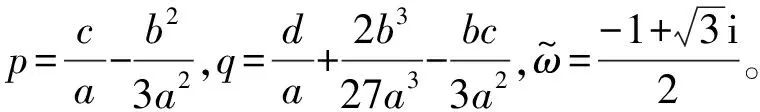
對于一般的Timoshenko梁，其波數的解析表達式為[17]

(10)

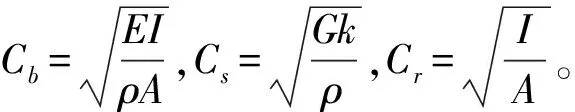
顯而易見，式(10)右端大括號外取“+”時，為兩組沿x軸負方向傳播的負行波；取“-”時，為兩組沿x軸正方向傳播的正行波。大括號中間的“±”如果取“-”，波數kb為純虛數，即傳播波；取“+”時，隨著頻率的增大，大括號里的數值會從正值變為負值，即存在一個波形轉換，振動波會從衰減波轉變為傳播波，這個頻率就是截止頻率。令式(10)的數值等于0即可得到截止頻率

(11)

對于質量偏心的Timoshenko梁，具有波形轉換特性的振動波數的平方對應的是表達式(7)，即當表達式(7)的值等于0時，此刻的頻率為質量偏心Timoshenko梁的截止頻率。根據一元三次方程求根理論，Δ<0時，表達式(7)的兩個三次方根計算出的值為一對共軛復數，在表達式(7)的值等于0時，可令：

(12)

(13)

對式(12)兩邊立方，可得：

(14)

在式(14)中消去τ，得到關于ω的方程，即：

27b6a()3q2()2+p3()3=0

(15)

(16)

其中，ac、bc、cc、dc在附錄中給出。求解此方程即可得到質量偏心Timoshenko梁的截止頻率ωc_E。

據卡爾丹公式，給出正實數解。式(17)即為存在質量偏心時，Timoshenko梁中彎曲波截止頻率的解析表達式

(17)

其中

接下來給出彎曲振動和縱向振動的振型函數。式(6)為λ的六次方程，則其根可表示為

(18)

故而振型函數可表示為

V(x)=Ceλx=

C1eλ1x+C2eλ2x+C3eλ3x+C4eλ4x+C5eλ5x+C6eλ6x

(19)

U(x)=Beλx=

B1eλ1x+B2eλ2x+B3eλ3x+B4eλ4x+B5eλ5x+B6eλ6x=

H(λ1)C1eλ1x+H(λ2)C2eλ2x+H(λ3)C3eλ3x+

H(λ4)C4eλ4x+H(λ5)C5eλ5x+H(λ6)C6eλ6x

(20)

根據式(4)，B和C之間存在如下關系

Bj=H(λj)Cj，j=1,2…,6

其中

(21)

質量偏心會引起彎-縱耦合振動，縱向振動便是通過H(λj)與彎曲振動聯系起來。

2 算 例

表1給出了一個圓形截面梁的幾何與物理參數，其中υ是泊松比，R是梁截面半徑，剪切因子k是根據Cowper[18]對圓形截面的研究所取。

表1 計算模型的參數

首先來考察質量偏心率對波數的影響，定義偏心率ee=e/R。

圖1給出了截止頻率隨質量偏心的變化，可以看出，質量偏心使得截止頻率降低，也就是那組彎曲振動衰減波會提前出現波數轉變，變為彎曲振動傳播波。

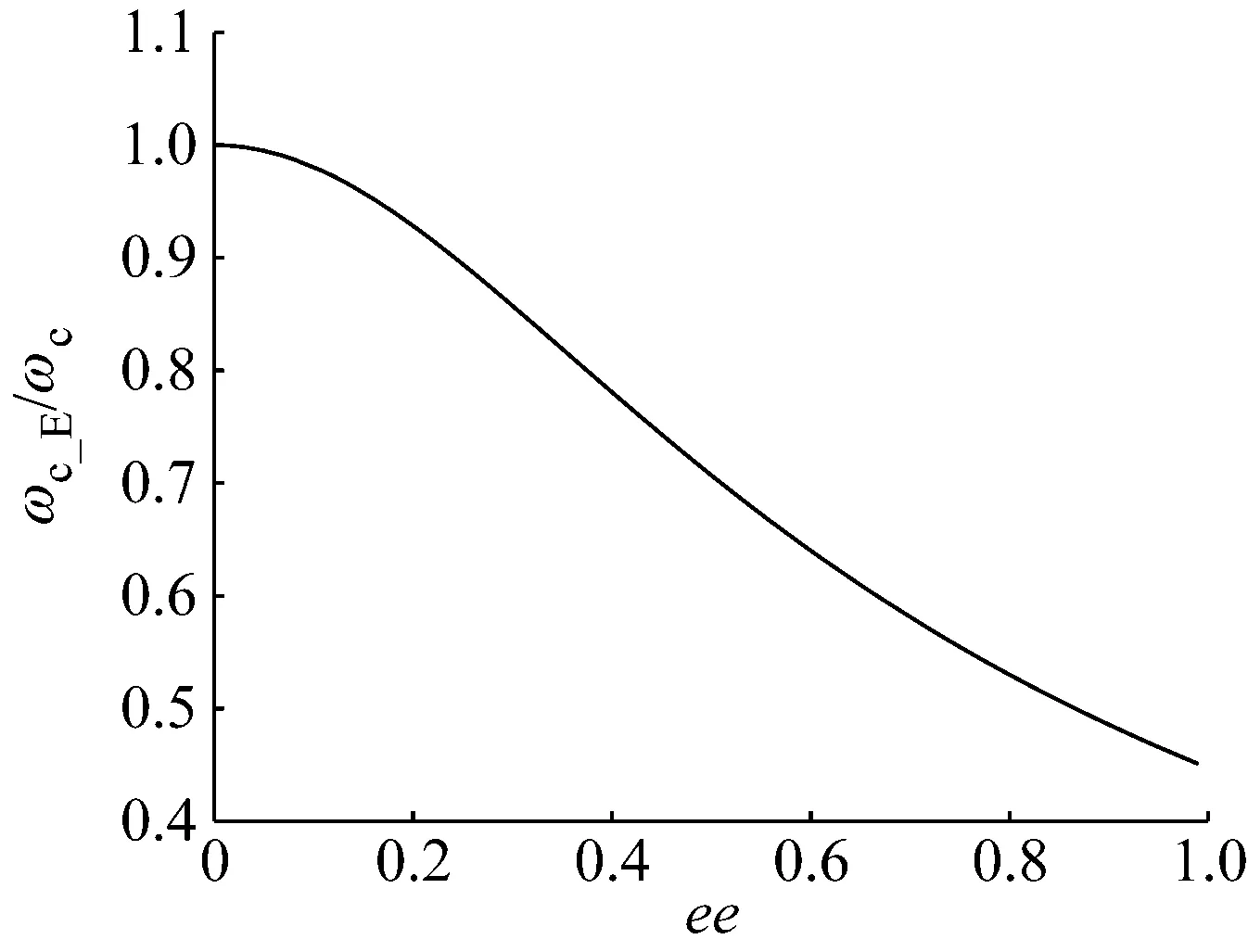
圖1 截止頻率隨偏心率的變化Fig.1 Variation of cut-off frequency with eccentricity

式(18)中的三組波數，每組波數互為相反數，因此只考察λ1、λ3、λ5。圖2給出了各種偏心率下波數λ1的變化情況，縱坐標Ω是頻率比，即Ω=ω/ωc。可以看出，λ1在低頻為彎曲振動的衰減波，無質量偏心時波數值在頻率比等于1處由純實數變為純虛數，也就是說λ1對應的振動波在截止頻率處由衰減波轉變為傳播波。存在質量偏心時也有同樣現象，只不過關鍵頻率隨著偏心率的增大會減小，使得波形轉變提前發生，與圖1結果吻合。

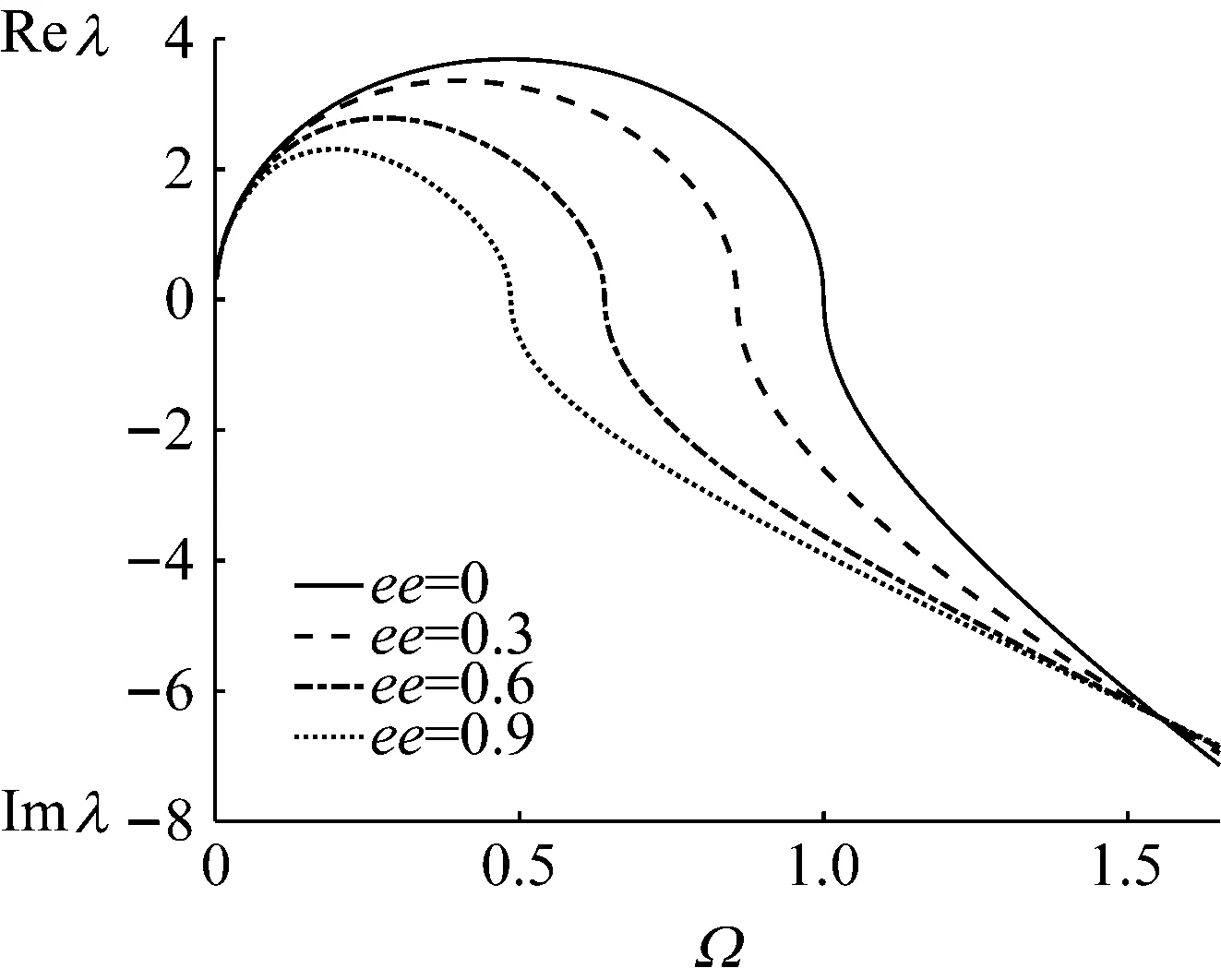
圖2 各種偏心率下的波數λ1Fig.2 Wavenumber λ1 under various eccentricity ratios

圖3給出了各種偏心率下波數λ3的變化情況。圓頻率的物理意義為單位時間上振動波相位的變化，波數的物理意義是單位空間上振動波相位的變化，它們之間通過波速互相聯系，圖3中曲線斜率的絕對值即為波速的倒數。對于非頻散波，波速恒定，其波數應為一條直線，可以看出，偏心率為0時也存在頻散現象，由此判斷λ3對應的彎曲振動波，且不論是否存在質量偏心，λ3對應的振動波始終為傳播波。

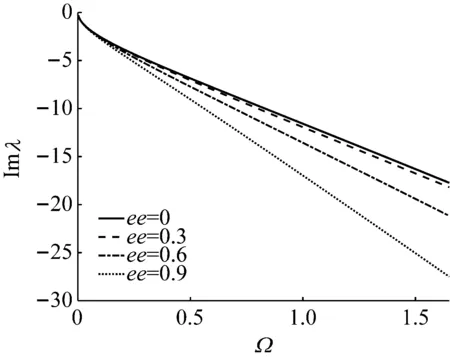
圖3 各種偏心率下的波數λ3Fig.3 Wavenumber λ3 under various eccentricity ratios

再來考察質量偏心下彎-縱振動的耦合情況。計算梁模型存在質量偏心率ee=0.3、0.6、0.9時的波數λ，代入式子(21)即可得到相應λ下的位移比H(λj)=Bj/Cj。不存在質量偏心時，縱向振動與彎曲振動是解耦的，也就不存在位移比。

圖4 各種偏心率下的波數λ5Fig.4 Wavenumber λ5 under various eccentricity ratios

圖5給出了ee=0.3時各波數對應的位移比。可以看出，λ1與λ3對應的位移比在低頻時較小，也就是彎曲振動占絕對優勢，隨著頻率上升，λ1對應的位移比中縱向振動明顯上升，當頻率比大于0.7時，位移比大于1，即λ1對應的縱向振動位移大于彎曲振動，在頻率比為0.8左右，也就是質量偏心Timoshenko梁的截止頻率處存在一個峰值。隨著頻率上升，λ3對應的位移比縱向振動有所上升，但是彎曲振動始終占主導地位。λ5對應位移比縱向振動位移占絕對優勢，但隨頻率上升，彎曲振動幅值變大，尤其當頻率大于截止頻率后，此波數對應下的縱向振動與彎曲振動位移比趨近于1。

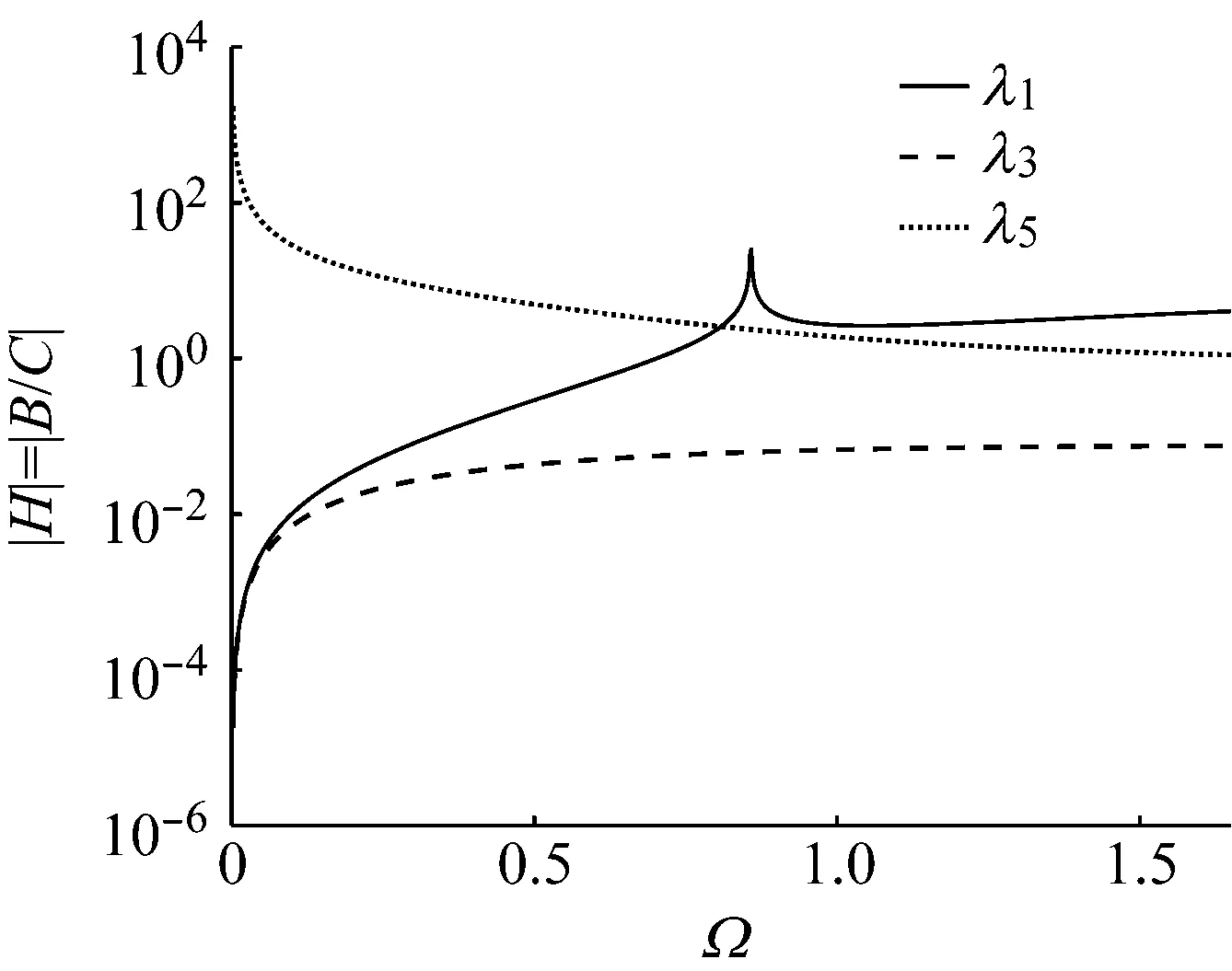
圖5 ee=0.3時各波數下的位移比Fig.5 Displacement ratio of wavenumbers under ee=0.3

圖6給出了三種偏心率下λ1對應的位移比，可以發現，質量偏心率越大，在頻率升高時，縱向振動所占比例的增加程度也越大。偏心率ee分別等于0.3、0.6、0.9時，頻率比Ω分別在0.70、0.48、0.36之后縱向位移大于彎曲位移。同時，三條曲線都在各自截止頻率處出現了峰值。

圖7給出了λ3對應的位移比，波數λ3對應的振動形式在低頻時彎曲振動占絕對優勢，雖然隨著頻率或質量偏心率的增大，縱向振動的成分會加大，但始終還是以彎曲振動為主。

圖8給出了λ5對應的位移比，波數λ5對應的振動形式在低頻時縱向振動占絕對優勢，隨著頻率或質量偏心率的增大，彎曲振動的成分會加大。偏心率ee分別等于0.6、0.9時，頻率比Ω分別在0.63、0.39之后彎曲位移大于縱向位移。

圖6 各種偏心率下λ1對應的位移比Fig.6 Displacement ratio corresponding to λ1 under various eccentricity ratios

圖7 各種偏心率下λ3對應的位移比Fig.7 Displacement ratio corresponding to λ3 under various eccentricity ratios

由于縱向位移通過質量偏心引入式(1)和(2)，即u=eθ，可以看出隨著偏心e的增大，彎曲對應的轉角引起的縱向位移也將增大，但θ與v并不是簡單的線性關系，因此，增大后的縱向位移u在λ5下會引起彎曲位移v的變大，即偏心的增大會加劇縱向與彎曲振動的耦合程度。這也就解釋了為何圖6、7中的位移比隨著偏心率的增大而增大，圖8中的位移比卻隨著偏心率的增大而減小。

圖8 各種偏心率下λ5對應的位移比Fig.8 Displacement ratio corresponding to λ5 under various eccentricity ratios

3 結 論

本文針對質量非均勻的Timoshenko梁，研究了質量偏心對其振動波的影響規律。推導了質量偏心下截止頻率的解析表達式，研究了三組振動波在質量偏心下的波形轉換，考察了三組波數對應的縱向-彎曲振動位移比，分析了彎-縱耦合隨頻率及質量偏心率的變化規律。得到了如下結論：

(1) 質量偏心會降低Timoshenko梁的截止頻率，偏心越嚴重，截止頻率下降越多。

(2) 質量偏心Timoshenko梁存在三組振動波，低頻下，前兩組以彎曲振動為主，第三組以縱向振動為主，在頻率或偏心率提高時，彎-縱耦合程度加劇，尤其第一、三組振動波，在超過一定頻率后，占主導的振動形式會發生變換。

(3) 第一組振動波在低頻時為衰減波，達到截止頻率后其轉變為傳播波，第二組、第三組振動波始終為傳播波，但質量偏心的存在使得第三組振動波其由非頻散波轉變為頻散波。

附錄A