電磁作動器出力特性及自適應抑制算法

張慶偉， 俞 翔， 閆政濤， 楊理華

(1.海軍工程大學 動力工程學院，武漢 430033；2.海軍工程大學 艦船與海洋學院，武漢 430033；3.江漢大學 智能制造學院,武漢 430056；4.海軍潛艇學院 動力操縱系，山東 青島 266199；5.中國科學院聲學研究所 噪聲與振動重點實驗室,北京 100190)

船用機械設備運轉產生的振動會在海水中形成復雜的低頻線譜噪聲[1]。隔振是降低機械振動傳遞的有效途徑之一，被動隔振在中高頻段表現較好[2]，但無法滿足艦船機械設備低頻振動隔離要求。主動隔振技術通過附加力源可有效抑制低頻振動，目前國內外已展開諸多研究[3-4]。

Zhang等[5]設計了一種主動壓電式作動器和橡膠被動隔振器相結合的混合隔振器，結構緊湊可靠性高，實現了共振頻率振幅明顯降低。Zhang等[6]設計了一種基于麥克斯韋法向應力的新型負剛度電磁作動器，可以提高靜剛度下的低頻隔振效果。劉露等[7]設計了一種壓電式作動器有效抑制了飛行器振動對儀器儀表的干擾。但以上作動器難以滿足對重量大、振動劇烈的船用機械設備隔振。李彥等[8]設計了一種空氣彈簧和磁懸浮作動器相結合的一體化隔振器，但磁懸浮作動器出力線性度較差，需要進行非線性補償，增加了控制難度。電磁式作動器能夠較好解決上述問題，通過輸出作用力來抵消線譜振動，適用于艦船設備的主動隔振。電磁作動器在一定范圍內輸出力與激勵保持線性關系，但受永磁體磁化強度限制，隨激勵增大將導致作動器進入飽和區。當控制系統受到強烈干擾時，將輸出較大控制信號，容易超出作動器工作電流范圍，導致隔振系統失效。為提高電磁作動器性能，石慧等[9]對作動器動子或定子形態、氣隙、倒角形式和線圈匝數等進行了優化分析；寧一高等[10]通過在不同工況下改變作動器的剛度降低力傳遞率來提高隔振效果；馬建國等[11]以降低鐵損耗和銅損耗為目標，對永磁體參數、磁極尺寸和匝數進行了調整。但始終因磁飽和現象，無法實現在強烈干擾或沖擊下的主動隔振。

本文對電磁作動器進行了仿真和試驗分析，為保證在強烈干擾下系統實現有效控制，提出了自適應抑制算法，仿真和試驗結果表明，該算法較好解決了作動器飽和影響，對雙頻激勵取得了顯著的控制效果，在受到沖擊時展現了較強的抗干擾能力。

1 電磁作動器

1.1 結構分析

電磁作動器由定子鐵芯、線圈、永磁體、動子鐵芯、簧片和動子芯軸等組成。其原理為線圈通入交流電產生交變磁場與永磁體恒定磁場相互作用輸出電磁力。其內部結構和動力學模型如圖1所示。

(a) 作動器結構圖

(b) 動力學模型圖1 電磁作動器結構圖及力學模型

作動器的動力學方程為

(1)

K(jω)I

(2)

式中：Br為永磁體剩余磁化強度;μ0為空氣磁導率;αleak為漏磁系數;agap為氣隙寬度;h為氣隙高度;l為永磁體高度;dmov為動子外徑;wpm為永磁體厚度;RAC(jω)為交流磁路磁阻;Rmov(jω)為永磁體磁阻。由式(2)可知，電磁出力與電流保持線性關系。

1.2 磁路仿真

基于COMSOL中AC/DC模塊磁場(mf)接口對作動器磁路結構進行電磁仿真。運用麥克斯韋張量法進行有限元分析，表達式為

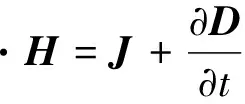
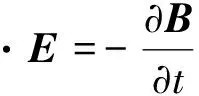
?·B=0

?·D=ρ

(3)

式中：J表示電流密度;ρ表示剩余電荷密度;D表示電位移矢量;E表示電場強度;本構關系為D=ε0εrE;B表示磁感應強度，H表示磁場強度，本構關系為B=μ0μrH+Br。各參數設置情況如表1所示。進行網格剖分，為保證計算精確，在出力區域細化處理。添加頻域計算，得到磁路仿真圖如圖2所示，色譜表示磁通密度模，線上箭頭表示磁路方向。

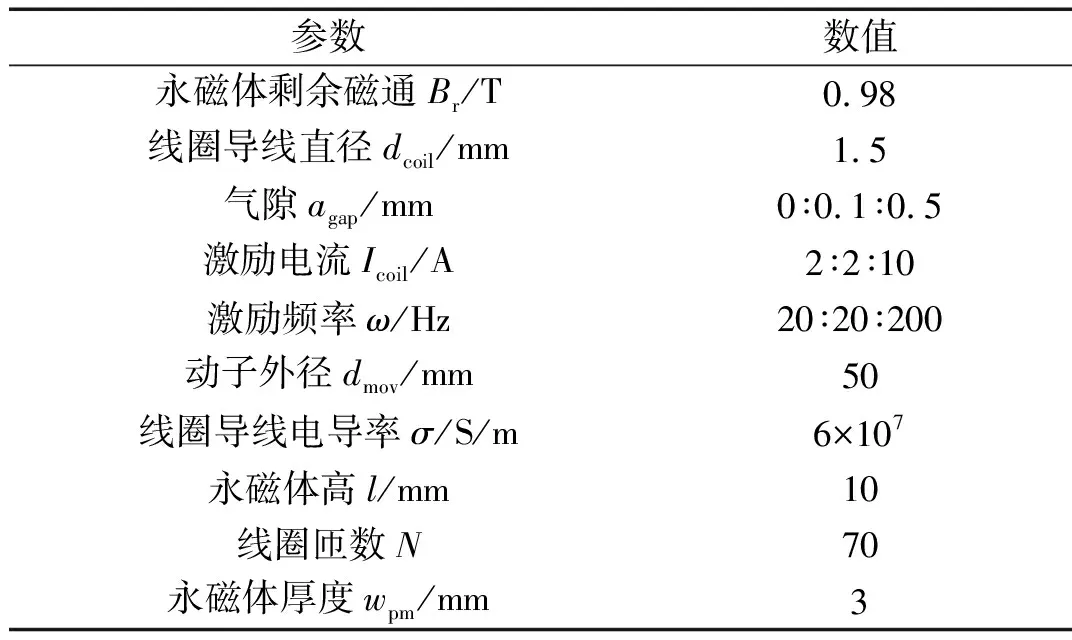
表1 磁路模型主要參數設置情況

對結果進行后處理，研究氣隙寬度agap對電磁輸出力的影響，結果如圖3所示。各激勵頻率在agap=0.3 mm輸出力達到最大值。在6 A電流、20 Hz頻率激勵下，輸出力能夠達到130 N。

圖2 電磁作動器磁路仿真圖Fig.2 Magnetic circuit simulation diagram of electromagnetic actuator

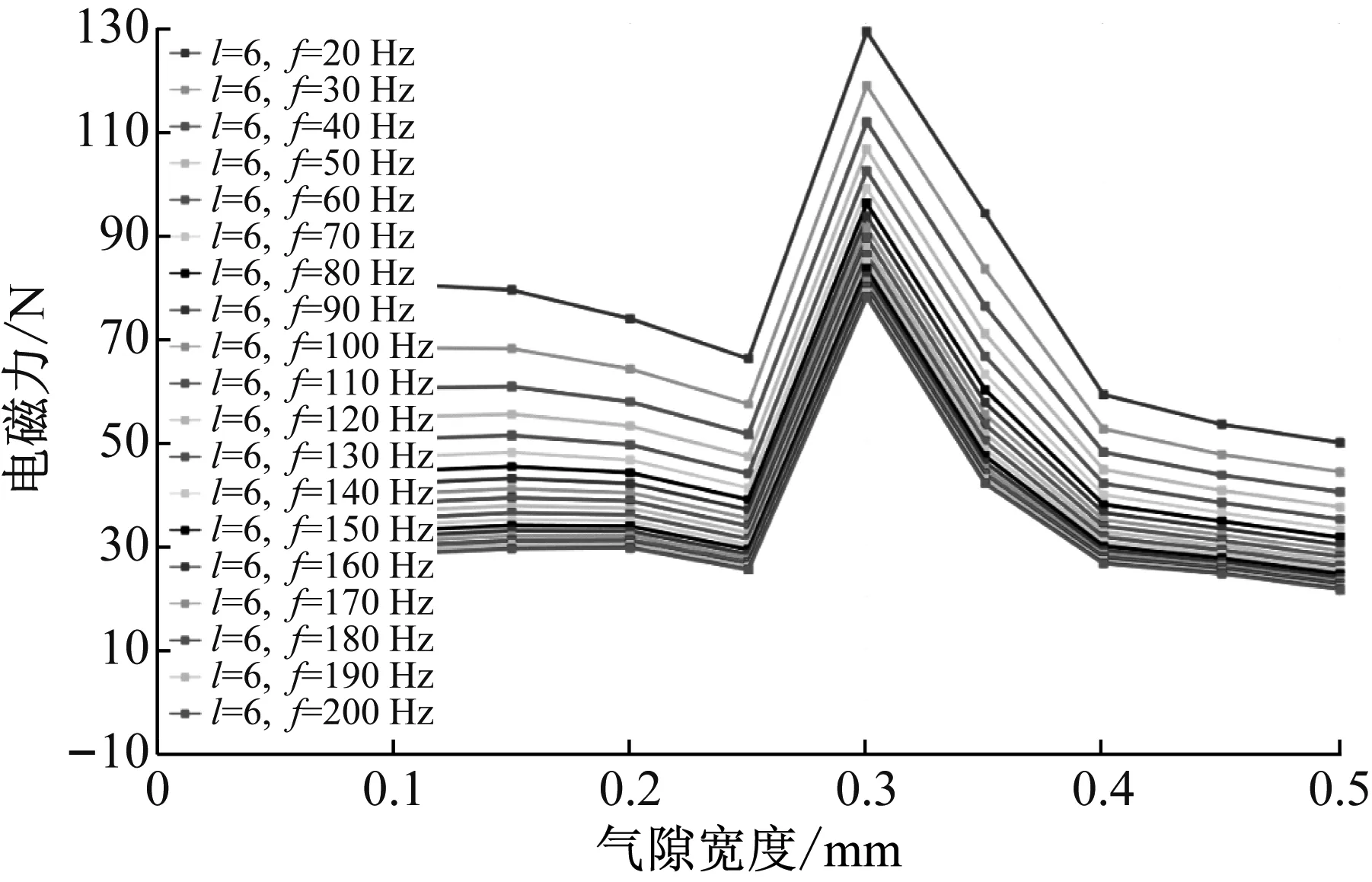
圖3 電磁作動器出力隨氣隙寬度變化值

研究電磁輸出力和電流、頻率關系，得到結果如圖4所示，仿真結果符合理論定性分析，電磁輸出力與電流保持線性關系。

圖4 電磁作動器輸出力隨電流變化關系Fig.4 The relationship between the output force of the electromagnetic actuator and the current

1.3 出力測試

電磁力的輸出需要經過動子鐵芯和簧片等機械元件才能到達隔振設備，搭建了電磁作動器出力性能的測試工裝，示意圖如圖5所示。

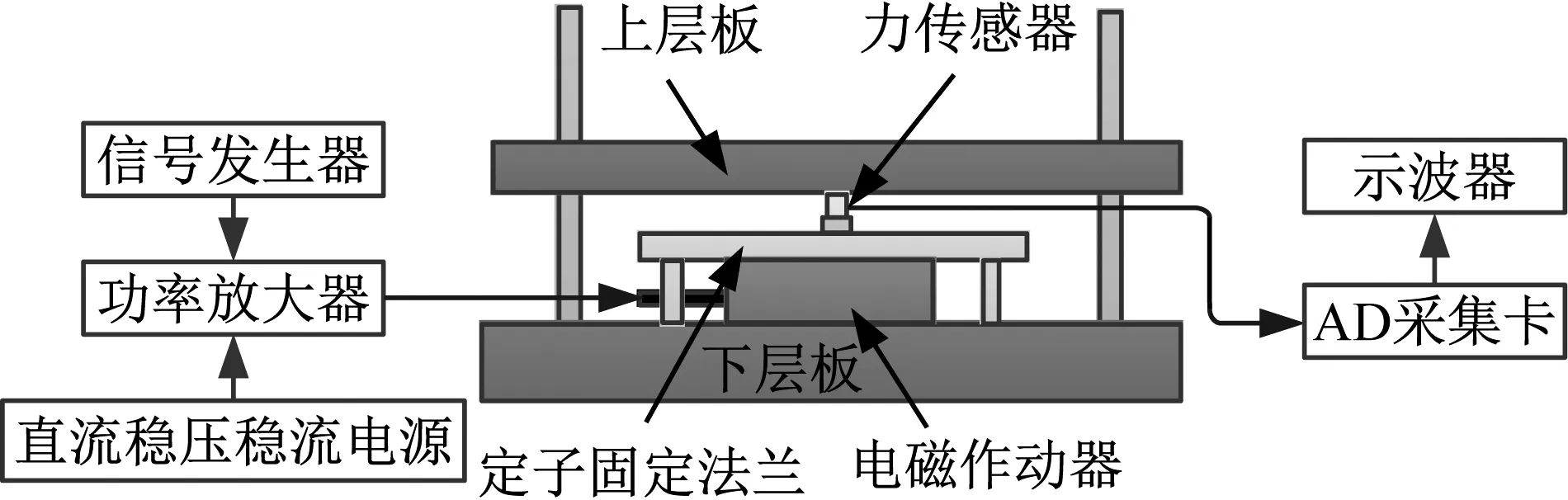
圖5 電磁作動器出力性能測試工裝Fig.5 Electromagnetic actuator output performance test tool

信號發生器按照一定的掃描方式輸出不同頻率、不同電流的正弦激勵給功率放大器，驅動電磁作動器，ICP型力傳感器對拉壓力進行測量，傳感器內置了專門的集成調理電路，AD采集板卡對力信號完成采集。得到輸出力測試結果如圖6和7所示。

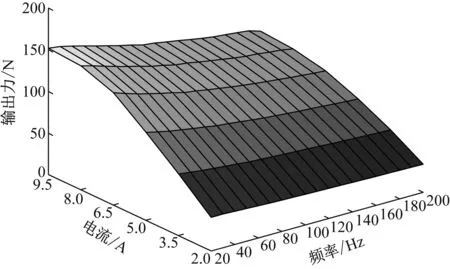
圖6 電磁作動器出力性能測試結果Fig.6 Test results of output performance of electromagnetic actuator

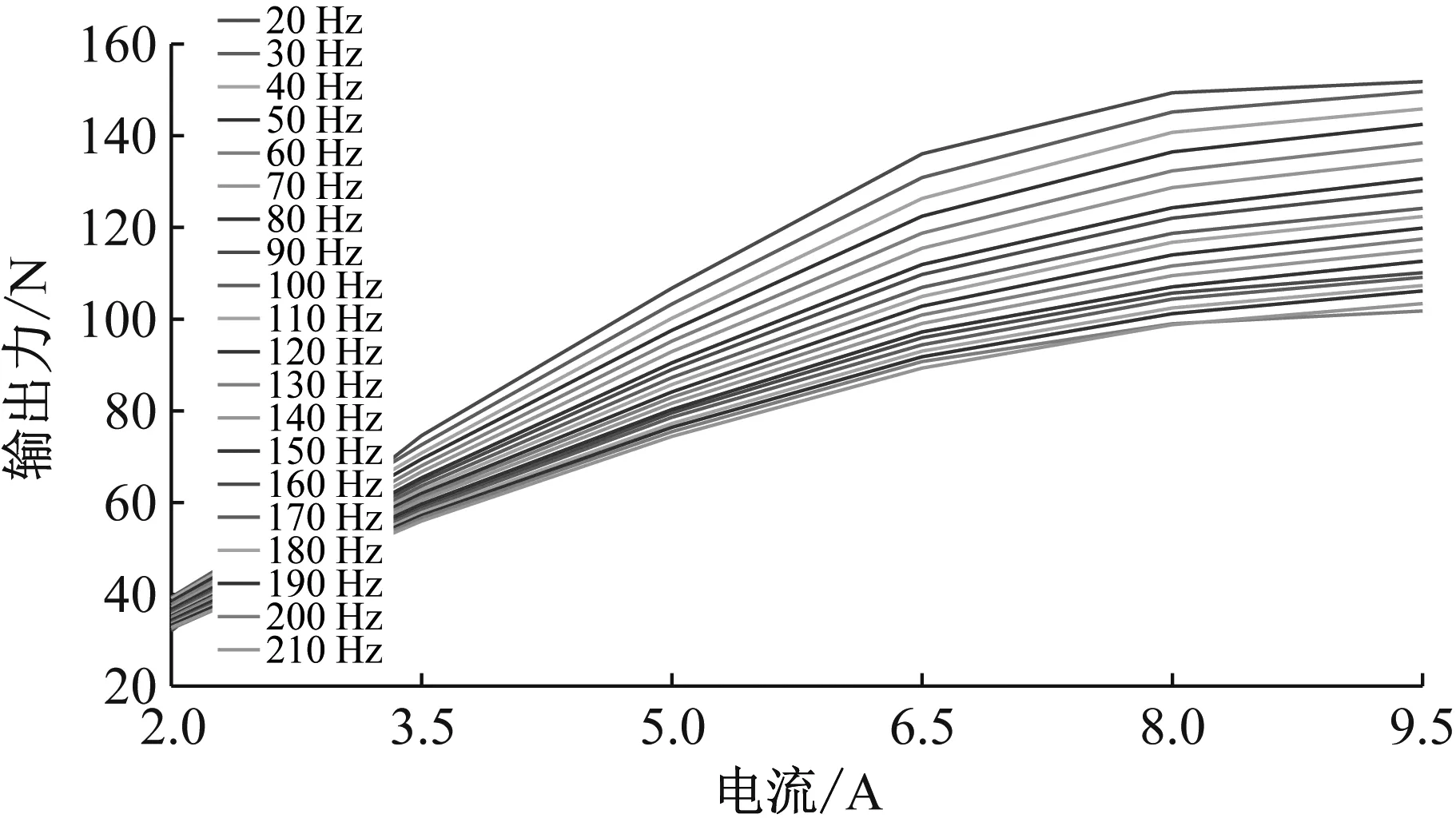
圖7 測試輸出力隨電流變化關系Fig.7 The relationship between Test output force and current

由圖7可知，在激勵電流6.5 A之前，測試輸出力與電流大小保持良好的線性關系，且與仿真結果吻合度較高。在6.5 A之后輸出力低于仿真計算結果，在8 A電磁力趨于平穩。其原因在于隨電流增大，當定子磁場強度達到一定時，永磁體的磁化強度達到飽和狀態。根據B-H磁化曲線可知，磁場強度H增大到一定程度，磁感應強度B不再增加，說明了電磁力的輸出因磁飽和而收斂到定值。

2 自適應抑制算法

在自適應控制過程中，當系統受到外界強烈干擾，誤差信號激增，引起控制權系數劇烈變化，使得輸出信號超出作動器有效工作范圍，最終導致系統發散失控。因此應對控制器的輸出信號進行約束，將幅值限定在作動器飽和區以內。本文在FXLMS算法基礎上引入抑制因子，對控制器權系數的更新進行調整。

FXLMS算法將最小均方算法與次級通道濾波結構相結合對權矢量w(n)進行更新，在主動控制領域被廣泛應用。其算法原理圖如圖8所示。

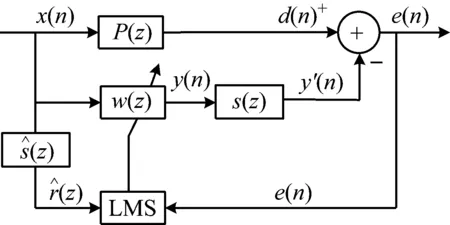
圖8 FXLMS算法框圖Fig.8 FXLMS algorithm block diagram

FXLMS算法的權系數迭代公式為

w(n+1)=w(n)+μ?(n)=

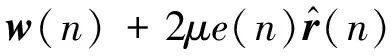
(4)

(5)

對控制器輸出信號進行約束，可寫為

(6)

式中：τ為約束閾值，sign(wTx)為取符運算，即當超出閾值時進行限幅，在范圍內時按式(4)原始進行更新。

在式(6)基礎上，為保證控制精度，引入拉格朗日函數求取條件極值，設定目標函數為

(7)

對w、λ分別求導

(8)

令式(8)結果均為零，得到

(9)

(10)

(11)

將Δw作為抑制因子引入式(4)對權系數更新進行修正，得到最終迭代公式

(12)

通過抑制因子的引入，當控制器輸出在τ值以下時式(12)等同于式(4)；當控制器輸出在τ值以上時Δw迅速減小至零，使得權系數更新幅值減小，輸出穩定在閾值附近，從而避免作動器進入飽和區。

根據式(6)輸出形式，可取反正切函數，如

(13)

得到其導函數為

(14)

式中：α為與閾值有關的系數，β可調整導函數窗寬。圖9為反正切函數及導函數圖像。

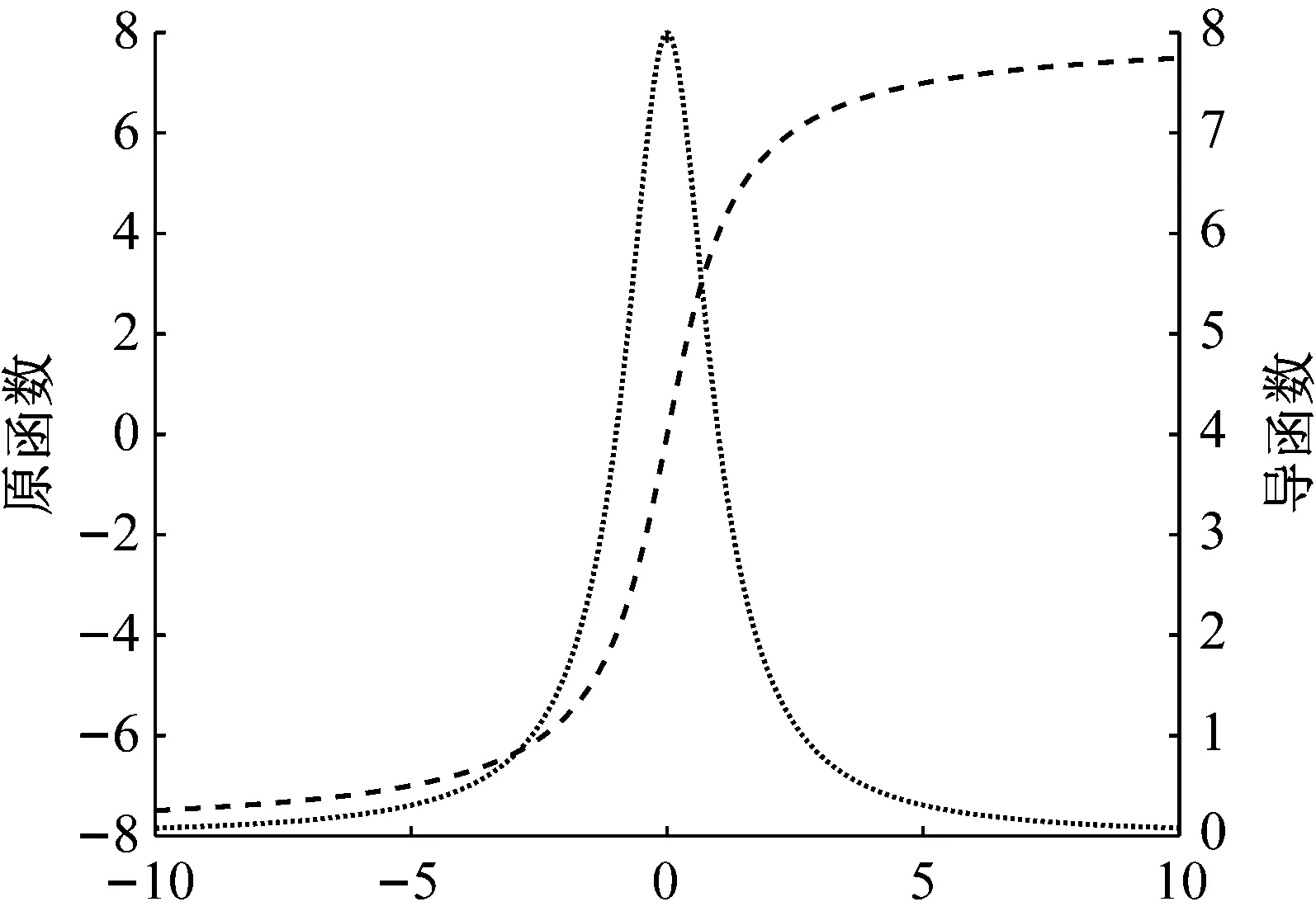
圖9 反正切函數及其導函數Fig.9 Arctangent function and its derivative function

3 仿真分析

對上述抑制算法進行仿真驗證，根據電磁作動器測試試驗，閾值τ設為8，表示作動器的最大輸入電流信號為8A。在實際控制中，為滿足式(6)要求，應分段處理，即設置不同的β，得到分段函數如式(15)所示。

(15)

采用頻率為37 Hz和60 Hz幅值均為8的雙頻諧波信號疊加信噪比20 dB的高斯噪聲作為參考信號。控制濾波器長度均為300階。算法迭代步長為0.000 1。得到各算法誤差信號控制前后時間歷程及控制輸出信號結果如圖10～12所示。

圖10為未考慮作動器飽和時FXLMS算法結果，未引入抑制因子時，控制器輸出信號明顯超出閾值。圖11為考慮作動器飽和，對超出閾值部分直接限幅處理，從圖11(b)可以看出，對輸出信號進行限幅相當于削波處理，不利于系統控制穩定性。在剛開始迭代時，輸出幅值在閾值以內，誤差信號得到了有效收斂，當超過閾值時，由于削波使得算法失效，導致系統發散。圖12為考慮作動器飽和，自適應抑制算法結果。由圖12(a)可知，誤差信號迅速實現收斂，表明了Δw的引入加快了收斂速度，且幅值降低了85%左右。由圖12(b)得到輸出信號較好約束在閾值以內，與圖11(b)相比，實現了平穩輸出，表明式(12)對輸出信號的可靠調整。根據仿真結果，證明了抑制算法對輸出信號的有效約束和振動的顯著控制。

4 試驗分析

進一步驗證算法可行性，采用NI PXI搭載RT系統進行主動隔振試驗。試驗對象為電磁激振器及附加配重，用來模擬中小型機械設備。將本文設計的作動器與被動隔振裝置有效集成為主被動復合隔振器，在無輸出力時具有較好的被動隔振效果和承載能力。試驗設備主要有NI PXI控制系統，Copley Xenus伺服驅動器，PCB加速度傳感器，電磁激振器，WYK-20040K直流穩壓穩流電源等，試驗臺架及原理示意圖如圖13所示。

(a) 試驗臺架

(b) 試驗原理示意圖

在試驗前先對系統次級通道進行離線辨識，利用20～200 Hz白噪聲激勵作動器，采用橫向FIR濾波器作為辨識模型，長度為200階。通過LMS算法不斷更新其權系數逼近次級通道真實傳遞函數，幅值曲線趨于平穩后辨識結束，得到次級通道矩陣并將其寫入下位機。

由信號發生器產生37 Hz、60 Hz雙頻幅值均為8 A諧波信號作為初始激勵信號。控制濾波器長度均為300階。算法迭代步長為0.000 03。采樣頻率設定為10 kHz，即滿足采樣定理，又保證對信號的實時跟蹤。針對AD板卡采集信號存在的50 Hz工頻干擾，在試驗中設計巴特沃斯帶阻濾波器進行濾除。以下層誤差信號傳感器采集的加速度響應作為評價標準，開啟主動控制前后信號的降幅即為隔振效果。在試驗進行2 s后，開啟算法控制。得到時頻域控制效果和輸入電流幅值如圖14、15所示。

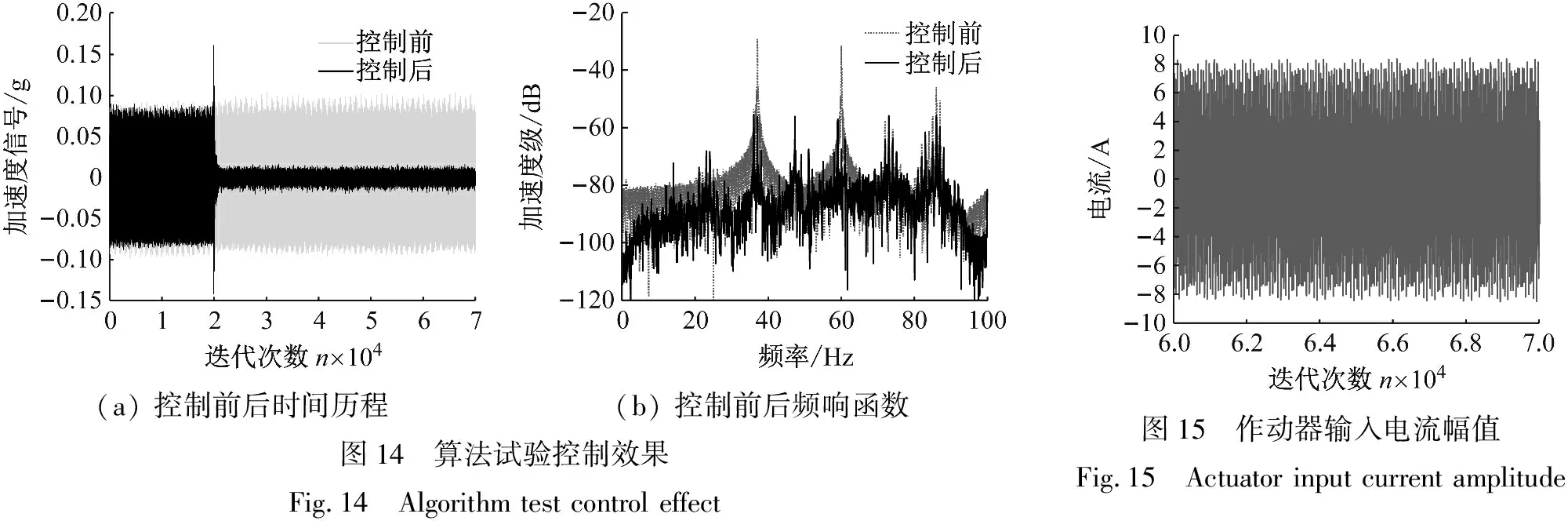
控制開啟后，在時域上誤差信號迅速得到收斂，且幅值降低了85%以上。在頻域上對37 Hz和60 Hz線譜分別衰減了27 dB和35 dB，控制效果較好。輸入電流也較好地約束在±8 A以內。試驗結果表明在較大干擾下，自適應抑制算法能夠較好約束輸出信號，保證電磁作動器在正常激勵電流內工作，實現了對振動的有效隔離。

進一步驗證算法魯棒性，在試驗運行到20 s時，對系統基座施加沖擊，誤差信號能夠迅速穩定，在21～22 s之間連續施加沖擊，誤差信號仍能夠快速穩定到收斂值。其加速度響應時間歷程如圖16所示。通過對系統不斷施加沖擊，說明了抑制算法仍能有效控制輸出信號，在誤差信號急劇增大時，控制器權系數能夠迅速回穩。因此得出算法具有較強的抗干擾能力。

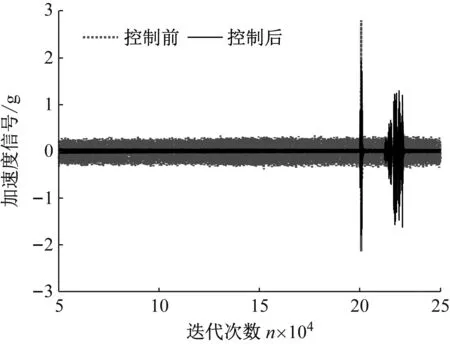
圖16 加沖擊后加速度響應時間歷程Fig.16 Acceleration response time history after shock

5 結 論

(1) 針對船用機械設備低頻線譜振動，電磁式作動器具有結構緊湊、輸出力大、承載能力大、線性度高等優點。通過對電磁作動器特性分析得出隨電流激勵增大，作動器會由于磁飽和而進入飽和區。當系統受到強烈干擾或沖擊，容易導致控制器輸出信號超出作動器工作電流范圍，使得控制發散。

(2) 為保證系統受到強烈沖擊不失效，通過引入了抑制因子對控制權系數更新進行修正，在閾值范圍內按原始信號輸出，當超出閾值時，權系數不再更新，輸出信號限幅。仿真和試驗結果表明，該算法較好解決了作動器飽和影響，對雙頻激勵取得了顯著的控制效果，在受到沖擊時展現了良好的控制魯棒性。