基于多尺度極差熵和專家森林的軸承故障診斷*

張書鋒,陳雪勤

(1.蘇州工業園區服務外包職業學院 信息工程學院,江蘇 蘇州 215123;2.蘇州大學 電子信息學院,江蘇 蘇州 215006)

0 引 言

目前,旋轉設備在軍工、能源、航空航天等領域已經得到了廣泛應用。由于滾動軸承是旋轉設備的關鍵部件,其健康狀況對設備平穩運行、生產安全具有重要影響。然而由于自身結構的復雜性和運行環境的惡劣性,滾動軸承容易發生腐蝕、磨損等損壞,從而影響生產安全[1]。因此,研究軸承故障診斷方法具有重要的意義。

當滾動軸承發生故障時,常會伴隨振動、溫度、聲音等物理量的變化,因此,滾動軸承故障診斷手段也包括聲學檢驗、油膜檢驗、電流分析與振動分析等[2]。由于傳感器具有便宜、安裝簡單、可在線高效診斷等優勢,基于振動分析的故障診斷方法得到了廣泛關注和應用[3,4]。

就方法而言,故障診斷主要包括故障提取和模式識別兩個方面,有些學者使用深度神經網絡將特征提取和模式識別一體化實現,這種方法提取的特征參數一般不具有實際物理意義[5]。多數研究中將故障提取與模式識別分開實現,提取的故障參數包括時域、頻域和時頻域參數等,模式識別方法包括支持向量機、神經網絡、隨機森林等。

文獻[6]針對特征提取和降維過程復雜的問題,提出了一種基于卷積神經網絡的故障智能診斷方法,有效地提高了軸承故障診斷的準確率。文獻[7]以原始信號的時域指標和小波包能量作為特征參數,并使用最小二乘支持向量機實現了故障模式識別,實現了軸承故障的較高精度診斷。文獻[8]提出了一種云特征與時域特征融合的故障特征提取方法,并使用改進人工魚群算法優化了支持向量機參數,經驗證,通過該方法可以獲得更高的識別準確率。以上研究成果在各自軸承故障診斷上取得了較好成果,但是不同使用環境下不同類型軸承的敏感特征差別較大、故障診斷準確率差別也很大,因此不同使用背景下軸承的故障特征提取和診斷方法仍是當前研究熱點。

筆者對滾動軸承故障特征提取與診斷技術進行研究,對極差熵進行改進,提取軸承振動信號的多尺度極差熵特征;筆者以隨機森林算法思想為基礎,給出基于專家森林算法的故障診斷方法,以達到提高軸承故障診斷精度的目的。

1 軸承多尺度極差熵特征提取

1.1 軸承故障分析

滾動軸承主要由內圈、外圈、滾動體和保持架等結構部件構成,其結構和主要參數如圖1所示。

圖1 滾動軸承結構及主要參數α—接觸角;d—滾動體直徑;D—軸承節徑,即滾動體中心間距離

當軸承發生內圈故障、外圈故障或滾動體故障時,軸承故障的特征頻率[9]如表1所示。

表1 軸承故障特征頻率

fIR—內圈故障特征頻率;Z—滾動體數量;fr—旋轉頻率;fB—滾動體故障特征頻率;fOR—外圈故障特征頻率

由表1中數據可知:當軸承內圈、外圈和滾動體等不同位置發生故障時,其特征頻率不同,也即故障信號的規律性不同。

軸承的特征頻率越大,則信號規律性越強,信號的熵值就越小;特征頻率越小,則信號規律性越弱,信號的熵值也就越大,因此,可以通過提取其信號的熵值特征,以此作為軸承的故障特征。

1.2 極差熵

極差熵對信號長度和信號幅值不敏感,具有較強的穩定性,因此,可以使用極差熵來度量信號的復雜度。

對于長度為N的時間序列x={x1,x2,…xN},極差熵的計算步驟如下[10]:

(1)

式中:m—數據長度,個;t—延遲時間,s。

(2)在重構相空間中搜索匹配樣本數量。根據熵與信號自相似的關系,借鑒重標極差分析思想,可以定義樣本距離為:

(2)

(3)

式中:r—相似容限;Ψ()—Heaviside函數。

(4)

(5)

1.3 多尺度極差熵

由于極差熵只是在一個維度上對信號復雜度進行度量,并提取出該信號的特征,其無法全面提取數據序列中的有用信息。

為了解決這一問題,筆者提出了能夠全面反映信號特征的多尺度極差熵的概念,即借助粗粒化思想,在不同尺度上將給定信號進行分解,而后計算信號在各尺度的極差熵。

粗粒化方法為:

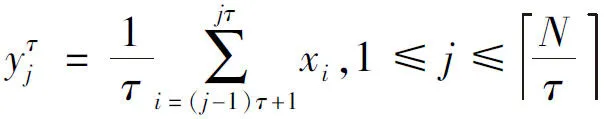
(6)

以τ=3為例,序列的粗粒化過程如圖2所示。

圖2 信號粗粒化方法

原始數據序列按照式(6)進行粗粒化后,按照極差熵的計算步驟得到信號在各尺度下的極差熵,從而得到多尺度極差熵。

1.4 特征參數降維

從原始信號中提取的多尺度極差熵對軸承故障的敏感程度不同,不敏感參數的存在不僅會增加特征向量維度,而且會降低故障識別準確率,因此,筆者使用主成分分析法[11,12]提取其高敏感特征。

筆者將提取的多尺度極差熵記為Y={yq1,yq2,…yqd}。其中:d為特征參數維度;q為特征參數數量，q=1,2,…,n。

首先，計算特征向量組成矩陣的協方差矩陣:

(7)

式中:Ry—協方差矩陣;

求協方差矩陣的特征值βq和特征向量vq,按照特征值降序將特征向量進行重新排序,得到新特征向量矩陣記為vq(new),將多尺度極差熵yq在新特征矩陣vq(new)中進行投影:

(8)

特征值βq越大代表相應的特征向量的貢獻率越大,則對軸承故障也就越敏感。因此,筆者選擇前若干個累積貢獻率足夠大的特征向量用于故障診斷,這樣就實現了特征向量降維。

2 專家樹森林故障模式識別

2.1 隨機森林算法

隨機森林算法原理如圖3所示[13,14]。

圖3 隨機森林算法

筆者使用Bagging隨機抽樣法從訓練集中隨機、有放回地選擇訓練樣本,從所選訓練樣本中隨機挑選特征屬性對決策樹進行訓練,得到訓練完畢的隨機森林決策樹[15];將測試集導入到決策樹中,得到各個決策樹的分類結果(即投票結果),得票數量最多的類別為隨機森林辨識的類別。

2.2 專家樹森林算法

分析隨機森林算法原理可知,森林中決策樹的投票權是無差別的,但是決策權重卻是一致的。為了解決這一問題,筆者提出了專家樹和專家森林的概念,即根據決策樹的決策能力為不同決策樹賦予專家屬性,依據決策樹的專家屬性為其賦予不同的決策權重。筆者將這種具有專家屬性的決策樹命名為專家樹,由專家樹組成的森林命名為專家樹森林。

筆者將訓練樣本分為訓練組和預測試組兩類,其中,訓練組用于決策樹的訓練,預測試組用于對決策樹的決策精度進行測試,從而為其賦予不同的專家屬性。

將預測試組的樣本數量記為C,則專家樹k在預測試中的決策準確率Rk為:

(9)

式中:Ck—專家樹k在預測試中決策正確的次數。

根據預測試的決策準確率,為專家樹k賦予的專家權值wk為:

(10)

式中:wk—專家樹k的專家屬性,即決策權值;K—專家樹數量。

則專家森林的決策結果為加權和取最大值的類別,即:

(11)

式中:fEF(x)—專家森林算法決策結果;Bk(i)—標識函數,當決策樹k識別結果為i時Bk(i)=1,當決策樹k識別結果不為i時Bk(i)=0。

2.3 專家森林算法流程

根據專家樹森林算法的構造方法,筆者設計的專家樹森林算法流程如下:

(1)初始化算法參數,包括決策樹數量、訓練組樣本數量、測試組樣本數量;

(2)將測試樣本隨機分為訓練組和預測試組;

(3)使用訓練組樣本對專家森林的決策樹進行訓練,并使用預測試組對決策樹的決策準確率進行評價,為決策樹賦予專家屬性得到專家樹;

(4)將測試樣本輸入到專家森林中,得到專家投票的加權和,加權和最大的類別為決策類別。

3 實驗及結果分析

3.1 數據獲取與特征降維

筆者使用美國凱斯西儲大學的滾動軸承故障數據進行實驗[16]。其中的測試軸承型號為6205—2RS深溝球軸承,轉速為1 797 r/min,數據采樣頻率為12 kHz。

軸承分為正常狀態、內圈故障、外圈故障和滾動體故障4種狀態,每種故障狀態下根據故障深度分為0.007 inch、0.014 inch、0.021 inch 3類,因此共有10類故障狀態,如表2所示。

表2 軸承10種狀態

在每一種軸承故障狀態下,筆者截取2 048個數據點,原始振動數據如圖4所示。

圖4 原始振動數據x—振幅;t—時間

取數據長度m=2,相似容限r=0.2SD,通過計算可得到不同尺度下軸承各狀態的極差熵值,如圖5所示。

圖5 不同尺度極差熵

由圖5可以看出:在軸承信號不同尺度的極差熵特征值中,一些極差熵(如1尺度、2尺度)對軸承故障敏感性好,狀態之間區分明顯;也有一些極差熵(如3尺度、4尺度)對軸承故障敏感性較差,故障狀態之間區分不明顯。因此,還要從特征參數中提取出對軸承故障狀態敏感的特征參數。

筆者使用主成分分析法計算上述多尺度極差熵的貢獻率,其結果如表3所示(按貢獻率降序排列)。

表3 主成分分析結果

由表3可以看出:上述25個多尺度極差熵的貢獻率相差較大,也即對軸承故障狀態的敏感度相差較大;選取貢獻率大于1%的前7個特征值組成特征向量,前7個特征值的累積貢獻率為96.24%,能夠較好地表征軸承的故障特征。

3.2 故障診斷及結果分析

為了對基于降維方法和專家樹森林算法的軸承故障診斷效果進行驗證,筆者設置了3組對比實驗。實驗一使用降維前的25個特征參數組成特征向量,依據隨機森林算法進行故障診斷;實驗二使用降維后的7個特征參數組成特征向量,依據隨機森林算法進行故障診斷;實驗三使用降維后的7個特征參數組成特征向量,依據專家樹森林算法進行故障診斷。

筆者從軸承每種狀態的振動信號中隨機截取102 400個點,并平均、非重疊地分為50個樣本,10種狀態下共得到500組樣本。每種狀態下隨機選擇10個樣本作為訓練組樣本,共100個訓練組樣本;再隨機選取10組樣本作為預測試組樣本,共100個預測試組樣本;每個狀態剩余30組樣本為測試樣本,共300組測試樣本。

3組實驗中針對300組樣本的診斷結果如圖6所示。

圖6 3組實驗診斷結果n—樣本編號

實驗一、實驗二和實驗三的故障診斷準確率如表4所示。

表4 故障診斷準確率

對比實驗一和實驗二可知:實驗二的故障診斷準確率比實驗一高17.07%,這是因為實驗二以降維后的高敏感特征參數作為特征向量,這也證明了基于主成分分析法的降維方法是有效的;

對比實驗二和實驗三可知:實驗三的故障診斷準確率比實驗二高3.47%,兩組實驗均以降維后的7個特征參數作為特征向量,實驗二使用隨機森林算法進行故障識別,實驗三使用專家森林算法進行故障識別,兩組實驗結果說明專家森林算法的識別準確率高于隨機森林算法。這是因為專家森林算法中依據決策樹的決策能力,為決策樹賦予了不同的專家屬性,使專家樹具有不同的決策權。

由此可見,基于專家森林算法方法的識別準確率高于基于隨機森林算法方法。

4 結束語

針對軸承故障特征提取與診斷方面的問題,筆者提出了一種基于多尺度極差熵的故障特征提取方法和基于專家森林的軸承故障診斷方法,并通過實驗的方式對以上方法進行了驗證。

研究結論如下:

(1)與極差熵特征比,多尺度極差熵提取了振動參數的多維度故障特征,能夠較好地代表軸承故障特征;

(2)經過主成分分析法降維,降維后的特征組合對故障模式敏感度高于降維前,降維后故障診斷準確率也高于降維前;

(3)在同等故障特征向量條件下,由于對隨機樹賦予了專家屬性,專家森林算法故障診斷準確率高于隨機森林算法。

后續研究中,筆者將針對軸承故障特征提取與模式診斷的一體化開展研究,并使用深度學習等方法提取振動數據的潛在故障特征,判斷出故障模式。