基于VMD與SVM的電梯鼓式制動器故障診斷研究*

郝家琦,徐金海,鮑超超,鄭雷駿,唐 波*

(1.中國計量大學 計量測試工程學院,浙江 杭州 310018;2.杭州市特種設備檢測研究院,浙江 杭州 310003;3.舟山市特種設備檢測研究院,浙江 舟山 316021;4.浙江大學 工程師學院,浙江 杭州 310027)

0 引 言

作為高層建筑輔助通行的工具,電梯在日常生活與生產中有著非常重要的地位[1]。

在電梯的使用過程中,隨著制動閘瓦的磨損,其制動性能會逐漸變差,制動器無法產生足夠的制動力,從而導致沖頂、溜梯等事故的發生[2]。為了確保電梯制動設備的安全、可靠運行,對電梯制動器狀態監測進行研究,對制動器運行狀態進行實時監測,及時對制動器的故障進行識別具有重要意義。

目前,對于制動器狀態的監測與診斷主要分為兩類:(1)基于經驗知識的監測與診斷;(2)基于數據驅動的監測與診斷。

基于經驗知識的監測與診斷,采用人工的方法對響應時間、閘瓦間隙量進行測量,以評估制動器性能是否滿足國標[3]。這些方法測得的數據精度低且操作復雜,需要投入大量的人力定期檢查,且無法對電梯的運行狀態進行實時監測與診斷。

基于數據驅動的監測與診斷分為直接與間接兩種。(1)直接方法。是對制動器的運行參數進行監測并診斷。賀無名[4]通過直接監測制動器制動過程中閘瓦的間隙信號,實現了對制動器進行的故障診斷;但是通過閘瓦間隙變化曲線無法對制動力矩不足進行精準的識別。趙海文[5]與胡立鋒[6]通過測量制動彈簧的彈性系數、閘瓦間隙、制動力矩的方法,來對制動器的性能進行評價;該方法需要在正常使用中的電梯主機上安裝大量的傳感器,目前該方法只能應用于臺架實驗上。(2)間接方法。指通過測量曳引機工作時的溫度、振動等參數來評價電梯的性能。王逸銘[7]通過熱圖像分析法,對電梯閘瓦的磨損狀況進行了檢驗;但是外界的溫度變化會使探測器的溫度發生變化,從而影響其工作,因而無法對其進行長期的狀態監測。

采用振動信號進行狀態監測與故障診斷的方法,具有精度高、不受環境影響、操作簡單等優點,因此目前被廣泛應用于各類機械故障監測中。徐金海[8]提取了電梯減速箱部件的振動加速度信號,借此對電梯的運行狀態進行監測。

作為非線性機電耦合系統,電梯在運行過程中往往伴隨著機械振動,振動信號可以反映其內部機械部件的運行狀態。然而,在電梯制動器的故障診斷領域中,目前還沒有僅通過振動監測來進行診斷的研究文獻。

綜上所述,筆者對制動器制動臂的振動加速度信號進行監測,使用變分模態分解(VMD)與樣本熵結合的方法,提取制動器故障信號的特征;借助松鼠搜尋算法(squirrel search algorithm, SSA)解決VMD參數的選取問題;最后采用支持向量機(SVM)實現對電梯鼓式制動器安全隱患與故障的識別與診斷。

1 基于參數優化VMD的特征值提取

1.1 變分模態分解的定義

VMD[9]是2014年由KONSTANTIN D提出的一種可變尺度的信號處理方法。該方法通過迭代計算,搜索變分模態的最優解,不斷更新各模態函數(intrinsic mode function, IMF)分量及中心頻率,進而對信號的頻率實現自適應剝分和個體分量的有效剝離。

對于原始信號f(x)，通過Hilbert變換后，再與相應模態的中心頻率指數e-jωkt混合，通過L2范數梯度的平方估計出各個模態的帶寬，構建出如下變分約束問題：

(1)

式中：?t—求解函數對于時間t的偏導數；K—模態分量的總個數；f(t)—待分解信號。

引入二次懲罰項因子α和拉格朗日乘子λ，將變分法約束問題變成變分無約束問題。

增廣拉格朗日函數表達式如下：

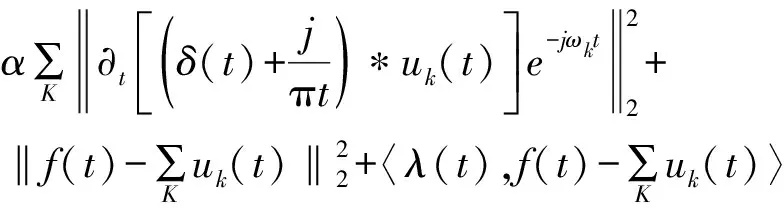
(2)

利用乘子交替方向算法(AMDD)，通過迭代{uk},{ωk}和λ，求得拓展拉格朗日的鞍點，獲得約束變分模型的最優解，將信號分解成K個IMF分量，來解決以上非線性問題。

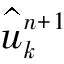
(3)

(4)

λ的更新表達式為：

(5)

式中：σ—更新因子。

{uk},{ωk}和λ按照上述更新表達式進行迭代，直到滿足終止條件，即：

(6)

式中：ε—收斂標準的容差，一般取1e-7。

1.2 基于松鼠算法的變分模態分解參數優化

為了增強信號特征的提取能力,需要對VMD分解的參數進行設置。根據VMD分解的一般步驟可得,模態個數K與懲罰因子Alpha對VMD算法的分解結果有決定性的影響,其余參數按照經驗值設置,不會對最終分解結果產生明顯影響。

由文獻[10,11]可知,當K取值過大時,會發生過分解現象,出現虛假的模態分量;當K取值過小時,會發生欠分解現象,導致模態混疊。Alpha的選取同樣對分解結果有影響,且當K固定時,Alpha的最優選擇呈現出不規律性。

根據上述分析結果,為了選定最優的VMD參數組合,需要使用優化算法,同時對K與Alpha進行參數尋優。由于受到不同的設備工作環境的影響,信號通常會比較復雜,難以對信號的模態個數進行評估。

在進行參數優化的時候,需要構建一個適應度函數作為評判的標準,為了獲得最好的VMD分解效果,筆者從能量與相關系數的角度構建了新的適應度函數。

信號經過VMD算法分解后,如果模式個數小于最佳值,則原始信號的某些頻率分量可能會在VMD分解過程中省略,出現欠分解現象[12]。

采用能量評判指標可以衡量原始信號與重構信號之間關系,即:

(7)

式(7)中,能量評判指標越接近1,重構信號中保留的原始信號能量越完整,信號分解得越完全,通過能量評判指標可以消除欠分解的情況。

當信號出現模態混疊現象時,與其他IMF分量相比,發生模態混疊的IMF分量的中心頻率更加接近周圍IMF分量的中心頻率。因此,筆者使用相關系數(correlation coefficient, Corr)作為判斷信號是否發生模態混疊的指標;相關系數定量描述了兩個信號之間的相似程度。

信號的相關系數準則為:

Corr

(8)

式中：Corr—IMF分量與原信號的相關系數；Corrmax—一組IMF分量相關系數的最大值。

當IMF分量的相關系數滿足上式時，則認為產生了過分解現象。

綜上所述，由于EI與Corr為相同的數量級，可以構建適應度函數，即：

(9)

當函數滿足相關準則，且(1-EI)*(1-Corr)最小時，可以認為信號的分解最完整，且不會出現模態混疊的現象。

SSA[13]是2018年由研究人員提出的一種簡單高效的新型優化算法。該算法具有收斂快、尋優強的特點。與傳統的粒子群算法與遺傳算法相比,SSA采取多策略更新模式,引入季節監測條件,從而不易陷入局部最優解,使得其準確率得到明顯提高。

因此,筆者通過使用SSA去解決VMD的參數全局尋優問題。

基于SSA的VMD最優分解參數流程圖如圖1所示。

圖1 松鼠搜尋算法流程圖

2 基于樣本熵與SVM的制動器故障識別

2.1 樣本熵的定義

樣本熵[14]是通過度量信號中產生新模式的概率大小,來衡量時間序列的復雜性;新模式產生的概率越大,序列的復雜性就越大。

一般地，對于由N個數據組成的時間序列{x(n)}=x(1),x(2),…,x(N)，樣本熵的計算方法如下：

(1)由原始信號構建m維向量：

Xm(i)={x(i),x(i+1),…,x(i+m-1)}
1≤i≤N-m+1

(10)

(2)定義向量Xm(i)與Xm(j)之間的距離：

d[Xm(i),Xm(j)]=maxk=0,…,m-1|x(i+k)-x(j+k)|

(11)

(3)對于給定的Xm(i)，統計Xm(i)與Xm(j)之間距離小于、等于相識容限r的j(1≤j≤N-m,j≠i)的數目，并記作Bm；

(4)增加維數到m+1，計算Xm+1(i)與Xm+1(j)(1≤j≤N-m,j≠i)距離小于、等于r的個數，記為Am；

(5)這樣，B(m)(r)是兩個序列在r下匹配m個點的概率，而Am(r)是兩個序列匹配m+1個點的概率。

樣本熵定義為：

(12)

樣本熵對數據長度的依賴性較小，抗干擾能力強。根據上文樣本熵的計算原理可知，計算樣本熵需要確定兩個參數，即模板匹配長度m與相似容限r。

根據文獻[15]可知，相似容限r為時間序列標準差的R倍，R的區間經驗值為[0.1,0.2]，模板匹配長度m通常設為1或者2。

2.2 基于支持向量機的電梯制動器故障識別步驟

支持向量機(SVM)是在統計學習理論的VC維理論和結構風險最小化原則的基礎上提出的一種機器學習方法[16]。它可以根據有限的樣本,在模型的復雜性與學習能力之間達到最佳的平衡,避免人工神經網絡產生“過學習”問題,因而通常被應用于分類與回歸問題。

隨著對SVM研究的深入,臺灣大學林智仁博士開發設計了LibSVM[17],該軟件包融合了SVM相關算法的優點,并采用了收縮與緩存技術,因此具有良好的性能,是目前被國際認可與采用的訓練算法。LibSVM作為通用的SVM軟件包,可以有效地解決多分類問題、回歸問題以及分布估計等問題,并提供交叉驗證,可以對所選取的參數進行優化。

為了對電梯鼓式制動器的故障進行診斷,筆者采用SSA搜索+VMD分解的最佳參數組合[K,Alpha],通過對原始信號進行VMD分解,得到最佳的IMF分量,并選取IMF分量計算樣本熵,將其作為特征向量,輸入LibSVM中,最后根據SSA選取LibSVM的最佳參數[c,g],實現制動器故障的分類與識別。

其具體的診斷步驟如下:

(1)通過采集系統獲取各種工況下制動臂的振動加速度信號;

(2)設置SSA的參數,通過適應度函數尋找最優參數組合,進而得到分解的最優IMF分量;

(3)根據分析結果,計算選取的IMF分量的樣本熵,并將其輸入到LibSVM中進行訓練;通過交叉驗證得到其準確率,將其作為適應度函數的SSA,得到SVM模型;

(4)將采集信號的測試集輸入步驟3中的SVM模型中,最終得到制動器的故障診斷結果。

3 實驗及結果分析

3.1 電梯制動器實測數據分析

筆者采用舜宇公司的LV-FS01激光多普勒測振儀對制動器的振動加速度進行測量。

測量系統包括激光探頭、測振儀主機、NI采集卡與PC。

測試驅動主機的型號為YJF-180,額定功率5.5 kW,轉速960 r/min,搭配的制動器型號為PXZD450/2.5-T2,額定推力為2*450 N。

電梯制動器圖例如圖2所示。

圖2 電梯鼓式制動器圖例

電梯運行過程為:當電梯啟動時,制動器通電,制動臂打開,曳引輪轉動,為電梯提供運行所需的曳引力;當電梯到達額定速度時,控制柜切換電梯運行模式從加速變為勻速;當電梯停止時,制動器斷電,制動臂抱閘,制動臂上的制動閘瓦摩擦制動輪產生制動力矩,使電梯停在指定位置。

筆者設置采樣頻率為6 250 Hz,采樣時間為20 s。當電梯啟動時開始計時,15 s時按下電梯停止按鈕。其運行過程包含電梯的整個運行流程。

正常狀態下制動器振動信號如圖3所示。

圖3 正常狀態下制動器振動信號

從圖3中可以看出:在制動器的工作流程中,存在制動器開閘、曳引機模式切換、制動器抱閘3個時間點。按時間依次排序方式,筆者將整個運行流程劃分為4個階段,即開閘階段、加速階段、勻速階段和減速階段。

當電梯出現帶閘運行的故障時,壓縮彈簧無法提供足夠的彈簧力,使制動臂不能完全打開。在這種情況下,在電梯運行的全過程中,其制動襯片都會對制動輪產生摩擦,從而導致其振動狀態發生變化;

當電梯出現制動力不足的故障時,制動臂無法提供足夠的制動力,使得制動輪不能快速停止,制動力發生的這種變化使得其在減速階段的振動狀態也發生變化。

經過對實驗數據進行對比可知:在每個區間內制動器振動信號的特征一致,且帶閘運行只會出現在加速與勻速階段,制動力不足只會出現在減速階段;帶閘運行對電梯加速階段與勻速階段的影響相同,且在實際運行時電梯勻速階段的運行時長遠大于加速階段。

為了能更直觀地對比分析電梯正常狀態與故障狀態,筆者分別從電梯運行的勻速階段與減速階段各選取0.5 s,對正常信號與故障信號進行對比。

其中,電梯運行各階段時域信號對比結果如圖4所示。

圖4 電梯運行各階段時域信號對比圖

從圖4可以看出:在正常工況下,最大峰值為0.145 3 m/s2,帶閘運行時加速度最大峰值為0.197 2 m/s2,故障狀態下有著更大的峰值。

由于電梯在減速階段振動特征呈現非穩態非周期的特點,從時域圖上無法直觀地分析出其區別。

電梯運行各階段頻域信號對比結果如圖5所示。

圖5 電梯運行各階段頻域信號對比圖

從圖5中可以看出:相比于正常狀態,帶閘運行的工況下,500 Hz處所對應的幅值明顯變大;在制動力矩不足的工況下,2 500 Hz附近信號頻率的峰值發生了偏移。因此,該特征可以作為判斷電梯是否發生了故障的依據。

但是時域與頻譜的對比存在問題,即無法準確描述正常與故障狀態下制動器振動信號的區別。為了能更準確地區分故障,通過對發生故障時的故障特征進行量化,能增強其特征的提取能力;采用變分模態分解的方法,分解出故障對應頻率的IMF分量,來判斷電梯制動器是否存在故障。

3.2 電梯制動器振動信號特征值提取

根據樣本熵的計算規則,時間序列越復雜,熵值就越大。為了更好地區分故障信號,筆者根據實際振動信號對時間序列標準差的倍數R進行不同取值,計算R在[0.1,0.5]區間時的樣本熵,得到其變化曲線。

其計算結果,即正常與故障狀態樣本熵變化曲線,如圖6所示。

圖6 正常與故障狀態樣本熵變化曲線

由圖6可以看出:隨著R的變大,正常與故障的熵值越來越接近;當R取0.1時,最容易分辨區分。

取R為0.1,計算的結果如表1所示。

表1 R=0.1時4種狀態的樣本熵值

由表1可知:在勻速階段制動力不足的故障工況下,樣本熵會比正常信號更大;在減速階段帶閘運行的故障工況下,樣本熵比正常信號小。

分析鼓式制動器工作機理可知:電梯的振動狀態與電梯的制動力的大小有關,制動力相當于制動系統中的激勵力;如果將勻速階段正常狀態看作制動力為零,則當制動力越大時,振動系統中的激勵力越大,樣本熵越小。

因此,通過對比R的不同取值,使得正常狀態與故障狀態的熵值區別變大,更容易區分兩種狀態。

筆者借助1.2節介紹的松鼠搜尋算法(SSA),搜索VMD在各個工況下最佳的[K,Alpha],獲得了2個階段正常與故障狀態的最優VMD分解參數,如表2所示。

表2 2個階段正常與故障狀態的最優VMD分解參數

根據3.1節的頻域分析結果可知,勻速階段的故障頻率表現在[0,1 500]區間,減速階段表現在[2 000,3 500]區間,所以應選擇該區間內的IMF分量作為故障的評判依據。

對表2中VMD參數進行分解,根據其結果可知正常與故障工況勻速階段前4階與減速階段后3階的IMF分量。

其中,勻速階段正常狀態VMD分解結果如圖7所示。

圖7 勻速階段正常狀態VMD分解結果

勻速階段帶閘運行VMD分解結果如圖8所示。

圖8 勻速階段帶閘運行VMD分解結果

減速階段正常狀態VMD分解結果如圖9所示。

圖9 減速階段正常狀態VMD分解結果

減速階段制動力不足VMD分解結果如圖10所示。

圖10 減速階段制動力不足VMD分解結果

3.3 基于LibSVM的電梯制動器振動信號故障診斷

根據3.2節對IMF分量選取的分析,筆者選取勻速階段前4個IMF分量與減速階段后3個IMF分量,并計算其樣本熵(以便于分別得到勻速階段4×80個熵值與減速階段3×80個熵值),將這些熵值組合作為特征向量,分別得到2個階段正常與故障狀態各80組特征向量;將特征向量輸入LibSVM中,通過SSA搜索SVM的最佳參數,得到勻速階段c=5.721 6,g=10.609 3;減速階段c=5.920 8,g=15.822 4兩組SVM參數。

筆者用訓練好的SVM分類器分別對兩個階段的正常與故障測試樣本進行分類,測試樣本的分類結果如圖11所示。

圖11 SVM測試結果輸出圖測試集樣本的存放順序為:勻速階段1～20為帶閘運行;21～40為正常狀態;減速階段41～60為制動力矩不足;61～80為正常狀態

從圖11中可以看出,筆者選用的優化參數VMD和樣本熵的特征值提取方法實現了對制動器帶閘運行與制動力矩不足兩種故障的識別,并且其識別率達到96%。

為了證明該方法的優越性,筆者采用傳統的EMD與固定參數VMD對信號進行分解,固定參數VMD算法的K=6,Alpha=2 000,提取特征值并將其輸入SVM,與采用該方法得到的準確率進行對比。

筆者分別選取分解的前3個IMF計算樣本熵,通過樣本熵構造特征向量訓練SVM分類器,用訓練好的SVM分類器對不同的工況下的測試樣本進行分類,其結果如表3所示。

表3 不同方法提取特征值的故障識別結果

由表3可以看出:采用EMD對數據進行處理時,對帶閘運行的故障識別率只有30%;在其余狀態下,識別率都低于VMD分解;

同時,與采用固定參數VMD方法相比,在每種狀態下,參數優化的VMD方法的識別準確率都有所提高。

綜上所述,基于該適應度函數的參數優化VMD分解具有優越的故障特征提取能力。

4 結束語

針對傳統電梯制動器診斷方法存在操作繁瑣、精度不高,且易受環境影響的問題,筆者提出了一種基于VMD與SVM的電梯制動器故障診斷方法,并將其應用于制動器振動信號數據實測,結果驗證了方法的有效性。

該研究的主要結論如下:

(1)適應度函數可以提升VMD的分解效果,避免出現過分解與欠分解等現象;相比于采用EMD分解和固定參數VMD分解的特征提取方法,采用適應度函數的參數優化VMD方法能有效地提高故障診斷的準確率;

(2)作為制動器運動系統的激勵力,制動力的大小影響其振動狀態;通過樣本熵可以建立制動力的大小與振動狀態的關系;

(3)通過采集制動器的振動信號,可以對制動器帶閘運行與制動力不足的常見故障進行識別。

采用該方法進行故障診斷,僅需要采集制動器運行時的振動信號,不受環境影響,且其精度較高。

但是由于受到試驗環境的限制,筆者采集到的數據有限。因此,在后續的研究中,筆者將結合試驗平臺采集到的更多數據,對電梯制動器剩余壽命預測模型進行研究。