空氣彈簧系統建模及其高度控制策略*

李子璇,鄔明宇,周福強*,危銀濤

(1.北京信息科技大學 現代測控技術教育部重點實驗室,北京 100192;2.清華大學 汽車安全與節能國家重點實驗室,北京 100084)

0 引 言

作為車輛底盤系統的重要組成部分,懸架系統連接著車架和車橋,并傳遞兩者之間的力和力矩[1]。懸架系統在汽車行駛的過程中扮演著重要角色,它影響著車輛行駛的安全性、乘客乘坐的舒適性和駕駛員操縱的穩定性[2]。

近年來,空氣懸架逐漸成為懸架系統一種新的發展方向,并且已經在大客車和重型載貨車上得到了廣泛的應用。而空氣彈簧的高度控制也逐漸成為一個熱點問題,因此受到了業界的廣泛關注。

空氣彈簧的精確控制需要精確的動力學模型[3-5]。李雪冰等人[6]運用虛功原理,推導出了空氣彈簧充氣結構的有限元方程,提出了空氣彈簧多變過程的有限元分析模型。孫麗琴等人[7]提出了一種帶連接管路附加氣室的空氣彈簧有限元模型。徐興等人[8]提出了一種全主動的電控空氣彈簧充放氣的動態數學模型,并對該模型進行了特性仿真分析。宋宇等人[9]運用拉格朗日方程方法,建立了空氣彈簧多剛體模型。BERG M等人[10]提出了一種基于實驗數據的空氣彈簧辨識模型。

但是以上這些動力學模型需要依靠數據的擬合或經驗來確定參數,因此前期需要大量的實驗數據,其擬合過程也較為復雜;同時,這些動力學模型不能夠準確地反映空氣彈簧氣室的充放氣過程。

對空氣彈簧的高度進行控制,需要滿足響應速度快、控制精度高等特性。江洪等人[11]以及PRABU K等人[12]提出了一種空氣彈簧高度的PID控制策略。KIM H等人[13]運用滑膜自適應控制技術,對空氣彈簧的車身高度進行了控制,并對空氣彈簧系統進行了仿真。徐興等人[14]結合空氣彈簧的動力學模型,分析了空氣彈簧系統振蕩現象的來源,并提出了一種變速積分式PID控制策略。GAO Z等人[15]運用靜態車輛高度調整平衡位置的狀態觀測算法,提出了一種模糊控制策略。MA X等人[16]針對整車提出了一種模型預測控制策略。CHEN Y等人[17]提出了一種線性二次最優控制策略。SHAN H Y等人[18]及LI H等人[19]提出了一種基于模糊神經網絡的算法。

另外,在對空氣彈簧的高度進行控制方面,反演控制[20]、H∞控制[21]等也都得到了應用。這些控制方法大都取得了較好的控制效果,但控制策略比較復雜,不便于實際的應用。

針對以上問題,筆者運用熱力學分析的方法,結合牛頓力學、流體力學等,建立不依賴于多方變化規律,充分考慮各種能量變化的空氣彈簧非線性模型,并建立四分之一車輛模型;在上述控制模型的基礎上運用PID控制理論,通過MATLAB/Simulink聯合仿真,以驗證模型和控制策略的有效性。

1 空氣彈簧系統模型的建立

1.1 氣路系統原理

某汽車空氣彈簧系統的氣路結構圖如圖1所示。

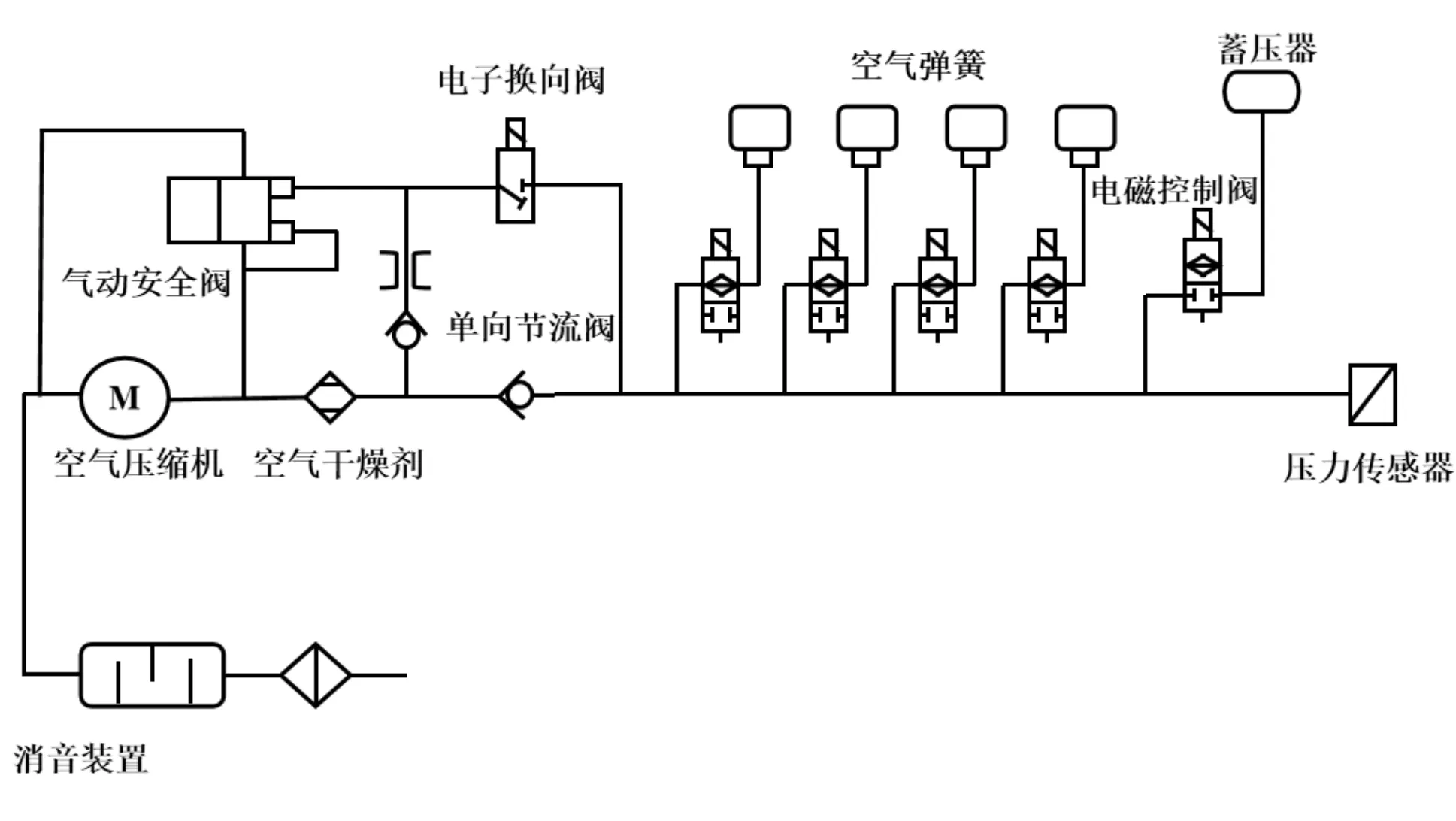
圖1 空氣彈簧系統氣路結構圖

空氣彈簧包括:空氣壓縮機、蓄壓器、空氣彈簧、電磁控制閥等主要部分。

空氣彈簧的充放氣過程是一個封閉回路,通過電磁閥來進行充放氣的切換。當車身需要升高時,打開高壓氣源控制閥以及空氣彈簧電磁閥,蓄壓器內高壓氣源流入氣室中,空氣彈簧充氣;當車身需要降低時,空氣彈簧電磁閥打開,氣室內的氣體流出,空氣彈簧放氣。

空氣彈簧系統利用控制電磁閥以及氣源控制閥,來控制空氣彈簧的充、放氣,以此來形成閉環空氣彈簧系統。

筆者以四分之一車輛空氣彈簧系統作為研究對象,可以很好地反映車輛的垂向振動。

四分之一車輛系統基本結構如圖2所示。

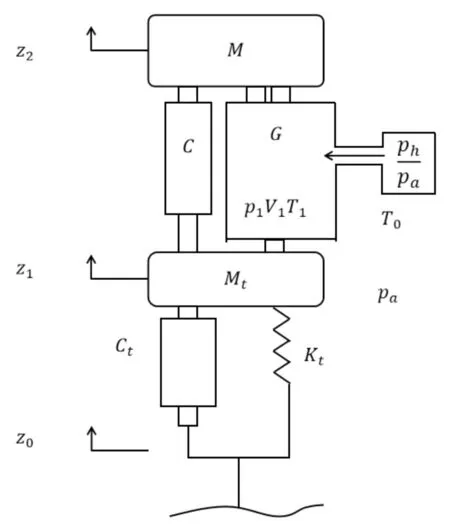
圖2 四分之一車輛二自由度模型M—懸掛質量;Mt—非懸掛質量;C—減震器阻尼系數;Ct—輪胎的等效阻尼;Kt—輪胎的等效剛度;G—外界輸入控制體的質量流量;p1—氣室內絕對壓強;pa—大氣壓;ph—高壓氣源氣壓;T0—大氣溫度;T1—氣室內溫度;V1—氣室內體積;z2—懸掛質量位移;z1—非懸掛質量位移;z0—路面激勵位移

1.2 氣路模型的建立

采用熱力學方法進行分析時,不需要多變指數,且采用的是確定的空氣比熱容比1.4,不需要復雜的過程來確定參數。采用熱力學第一定律,可以清楚地反映出不同物理過程對應的能量變化。

筆者以氣室內的氣體作為控制體,對氣體狀態方程進行微分:

(1)

式中:p1—氣室內絕對壓強;V1—氣室內體積;m1—氣室內質量;T1—氣室內溫度;R—氣室內氣體狀態常數;G—m1的變化率,即外界輸入氣體的質量流量,充氣時為正,放氣時為負,無控制指令時為0。

根據熱力學第一定律:

dQ+dW+dH=dU

(2)

式中:dQ—外界傳遞給氣室的熱量;dW—外界對氣室內氣體所做的功;dH—外界輸入氣體質量所帶來的能量;dU—氣室內氣體內能的增加量。

其中:

(3)

式中:Kh—氣室的導熱系數;CP—空氣的定壓比熱容;T1C—氣室與管路連接處的溫度;CV—空氣的定容比熱容。

將式(3)代入式(2)中,并除以dt可得:

(4)

結合公式(1),假設T1=T1C,便可以得到空氣彈簧的微分方程:

(5)

式中:FAS—氣囊產生的作用力;A—空簧氣室作用力與氣室內相對壓強的比值;γ—空氣的比熱容比;R—理想氣體常數。

由于氣室的幾何性質也會影響動力學特性,氣室體積與有效面積對高度的變化規律為:

(6)

式中:V10—初始狀態下氣室的體積;A0—初始狀態下氣室的有效面積;Vh—體積隨高度的變化率;Ah—有效面積隨高度的變化率。

1.3 四分之一車輛模型的建立

直接控制車身高度的質量流量G與氣路連接管路模型密切相關。管道內流體的流動如圖3所示。

圖3 管道簡化模型圖

圖3中,氣流從上流高壓pu處流向下流低壓pd處。

連接空氣彈簧和蓄壓器管路的流動特性非常復雜,筆者將其簡化為一個等效的節流孔,用公式表示為:

G=(pu-pd)C1

(7)

式中:C1—節流孔等效系數。

根據四分之一二自由度車輛模型,筆者建立了動力學方程如下:

(8)

式中:Mt—非懸掛質量;C—減振器阻尼系數;Ct—輪胎的等效阻尼;Kt—等效剛度;M—簧下質量;z0—路面激勵。

筆者結合公式(5～8),假設充放氣過程中,氣室內的氣體很快到達均一狀態;并且考慮到現實問題,假設車高調節過程中溫度與大氣溫度近似相等。

經過簡化其動力學模型,可以得到四分之一車輛模型的動力學方程為:

(9)

(10)

2 空氣彈簧高度PID控制策略

2.1 PID控制

PID控制策略具有結構簡單、穩定性高、易于操作等優點。在控制對象較為復雜的情況下可以采用PID控制策略。

PID控制器系統原理框圖如圖4所示。

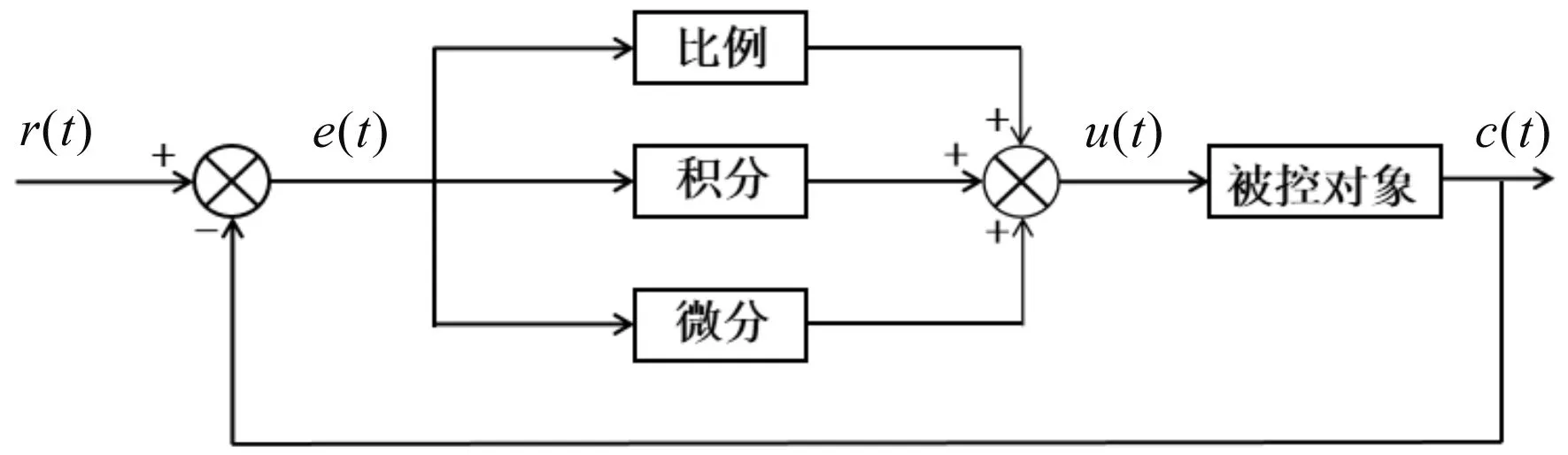
圖4 PID控制器系統原理框圖

圖4中,誤差信號e(t)為給定值r(t)與實際輸出值c(t)的差值,用公式表示為:

e(t)=r(t)-c(t)

(11)

筆者對誤差信號e(t)分別進行比例(P)、積分(I)和微分(D)的組合控制,控制器的輸出量作為被控對象的輸入量。

其基本控制規律為:

(12)

式中:KP—比例系數;TI—積分時間常數;TD—微分時間常數。

2.2 控制策略

空氣彈簧的閉環控制基本邏輯圖如圖5所示。

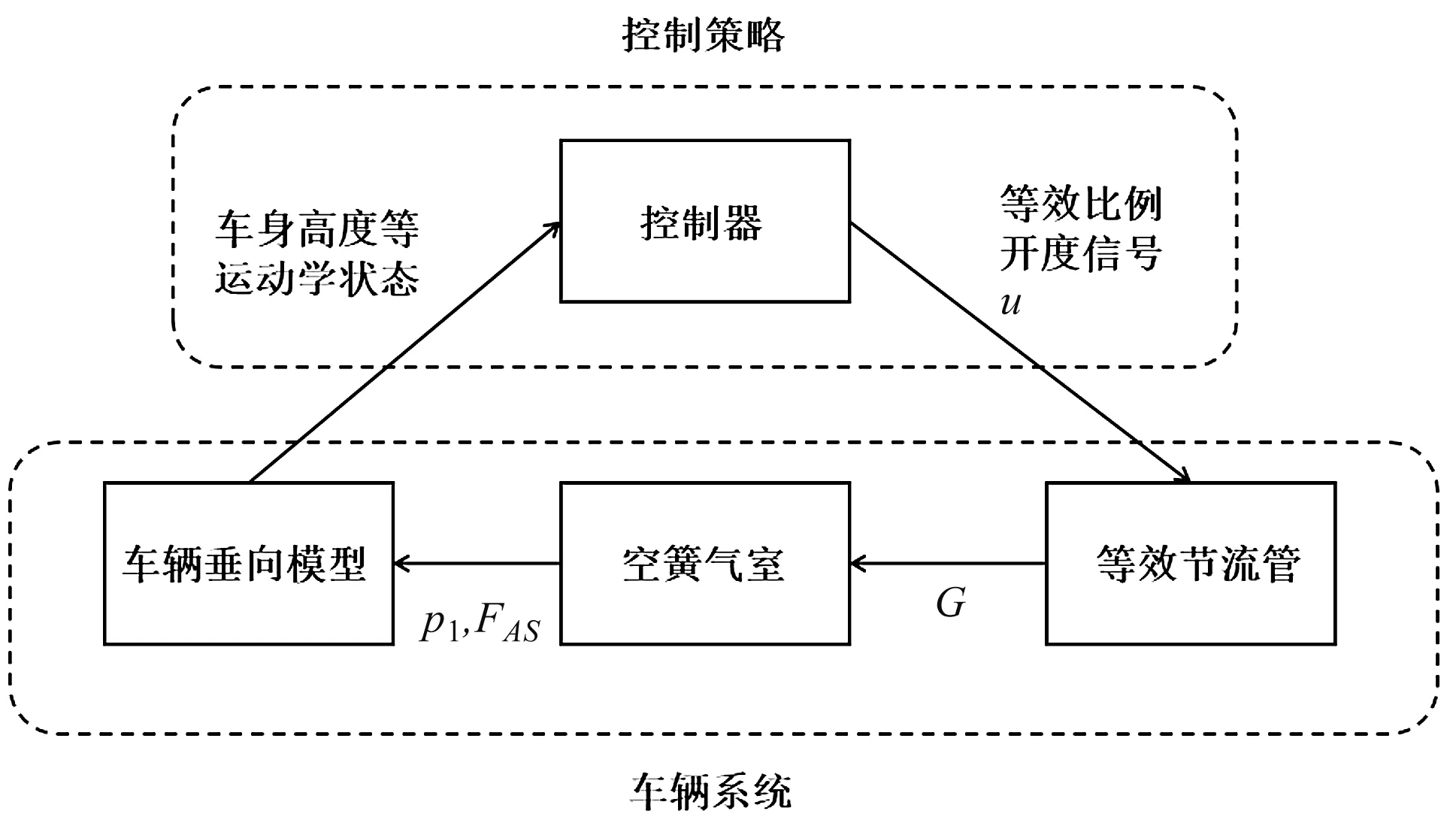
圖5 空氣彈簧閉環控制基本邏輯圖

圖5中,筆者以節流電磁閥的等效比例開度信號u作為系統的輸入量,車輛垂向模型反饋的車身高度等狀態量作為系統的輸出量,改變氣室內氣體的體積,以此來對車身高度進行控制;

由等效節流管模型轉化為氣流質量流量G,通過電磁閥間接實現對G的控制。u取值0或1,當u=0時,相當于電磁閥關閉,G=0;當u=1時,相當于電磁閥打開,G=△P·C。

u可以通過改變調制波占空比來實現,短時間的脈沖會影響電磁閥使用壽命;輸出控制量時設置一個死區,可以減小電磁閥的損耗。

3 仿真與結果分析

為了驗證四分之一車輛模型和控制策略的有效性,筆者利用MATLAB/Simulink仿真平臺建立空氣彈簧動力學模型,并對其進行聯合仿真。

仿真輸入參數和PID控制參數如表1所示。

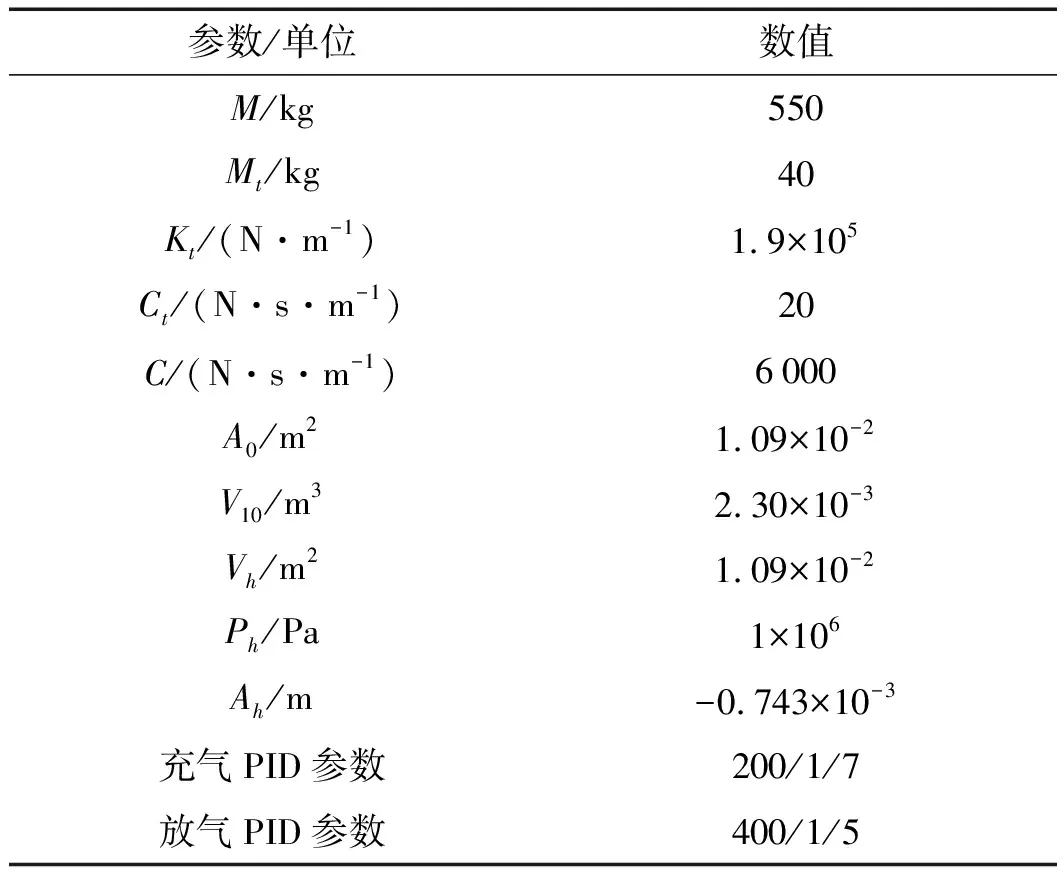
表1 仿真車輛輸入參數和PID控制參數

仿真過程是針對車輛行駛于C級路面時,對其進行高度調節。在初始高度的基礎上,筆者設置先升高20 mm,再下降20 mm,再下降20 mm,最后再升高20 mm的控制操作。

吳業平雖然只是主持工作的副庭長，但的確頗有點“能量”。他一方面極力為黑社會提供保護；另一方面，放膽收受周幫海的賄賂。如2011年至2013年，周幫海為幫其組織成員夏葉飛等人擺平聚眾斗毆、尋釁滋事、故意傷害等案件，先后共行賄近14萬元。吳庭長來者不拒、有求必應。多年來，無論案件性質是涉黑還是涉賭，抑或涉黃，他全然不管，只要對方給好處，就會盡全力。據悉，當地公安機關曾多次抓捕該團伙成員，但令人費解的是，這些黑社會成員，不論犯罪情節輕重，縣法院往往都只判處緩刑，沒幾天就被放出來繼續招搖過市。

采用路面濾波白噪聲模型,可以得到隨機路面的激勵曲線。車速選擇為50 km/h時,仿真曲線如圖6所示。

圖6 C級路面車速50 km/h激勵曲線

車輛高度控制過程中的仿真情況如圖7所示。

圖7 車輛高度控制仿真情況

在動態高度控制仿真中,相比于無PID控制和有PID控制的結果,車身平衡位置穩定后的高度誤差均方根值(RMSE)為:

(13)

式中:N—工況結束后車身平衡位置穩定時間段采樣點個數;err(k)—第k個采樣點對應高度與目標高度的偏差。

不同工況下,無PID控制和PID控制的RMSE值如表2所示。

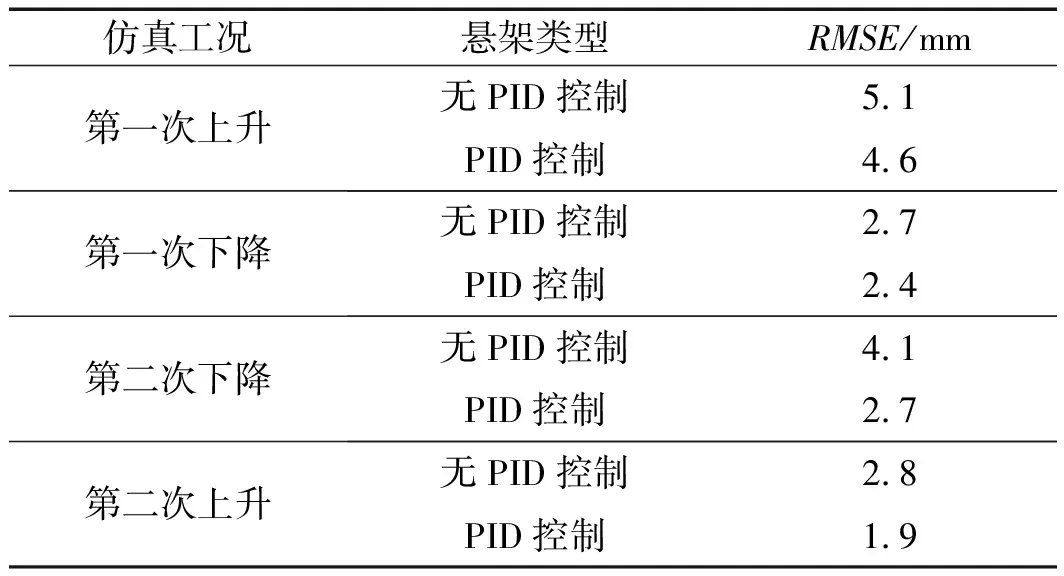
表2 車身位置穩定后高度RMSE

表2結果表明:

通過對比可知:采用PID控制策略的高度誤差均方根值更小,控制精度有所提升;相比于無PID控制器的情況,采用PID控制器RMSE改善率最高可以達到34.1%。該結果表明,其控制精度得到了提高。

4 結束語

通過采用熱力學分析的方法,筆者建立了不需要依靠數據擬合或經驗確定的空氣彈簧模型,在PID控制方法的基礎上設計了車身高度調節控制器,并對控制器的控制效果進行了仿真分析。

主要結論如下:

(1)所建立的以溫度、壓強為自變量的高精度非線性空氣彈簧模型,可以準確地描述空氣彈簧的非線性動力學特性;由于熱力學是自然界普遍存在的規律,在空簧模型方程中所使用的自變量是通用的,該結果具有普適性;

(2)由無PID控制和有PID控制的對比結果可知,相比于無PID控制器的情況,采用PID控制器RMSE改善率最高可以達到34.1%;其控制精度得到了提高,在實際應用中具有重要意義。

在下一階段的研究過程中,筆者將繼續對熱力學空氣彈簧模型進行優化,對節流孔部分進行細致分析,以得到更加完備的空氣彈簧氣室模型;同時,在控制方面,將模糊PID控制與變速PID/PWM控制策略應用到熱力學分析的空氣彈簧氣室模型上,以對其控制策略進行更加深入的研究。