基于開環補償與魯棒控制的電液位置伺服加載系統研究*

梅魯海,劉哲緯

(浙江機電職業技術學院 自動化學院,浙江 杭州 310053)

0 引 言

電液伺服控制系統在機械、交通、電氣和軍工等領域都有普遍的應用,而位置伺服系統是電液伺服控制的重要組成部分。

一般的位置控制方式有:PID閉環控制、模糊控制、自適應控制和滑模變結構控制等。位置控制技術一般包括動態模型建立、參數識別、控制系統仿真、優化控制算法、協同控制設計等。在通常的情況下,電液伺服系統不需要預先進行迭代辨識[1]。因為系統模態和參數是已知量,由此可以直接進行動態模型的創立和各種控制器設計。然而,一般的電液伺服系統的位置控制往往需要面對負載擾動和非線性參數等問題,且參數的波動往往是大范圍和不確定的,這時用傳統的閉環PID控制策略或擾動補償方法往往難以奏效。

目前,針對上述問題的解決辦法中,比較先進的是采用魯棒模型預測控制器設計、粒子群模糊邏輯控制器設計或進行離散滑模控制算法等。這樣,在被控對象的非線性擾動大幅變化時,采用這些技術的電液伺服系統仍可以自動保持最佳的工作狀態、穩態精度與動態品質。

為此,筆者搭建一套較為完整的電液伺服加載試驗臺系統,建立試驗臺系統的數學模型,提出抑制擾動的開環補償方法,對期望軌跡規劃的位置開環補償控制方法進行分析,對位置伺服控制器的模型進行論證。

1 試驗臺系統結構與數學模型

1.1 系統結構

筆者研究的電液伺服試驗臺系統的結構圖如圖1所示。

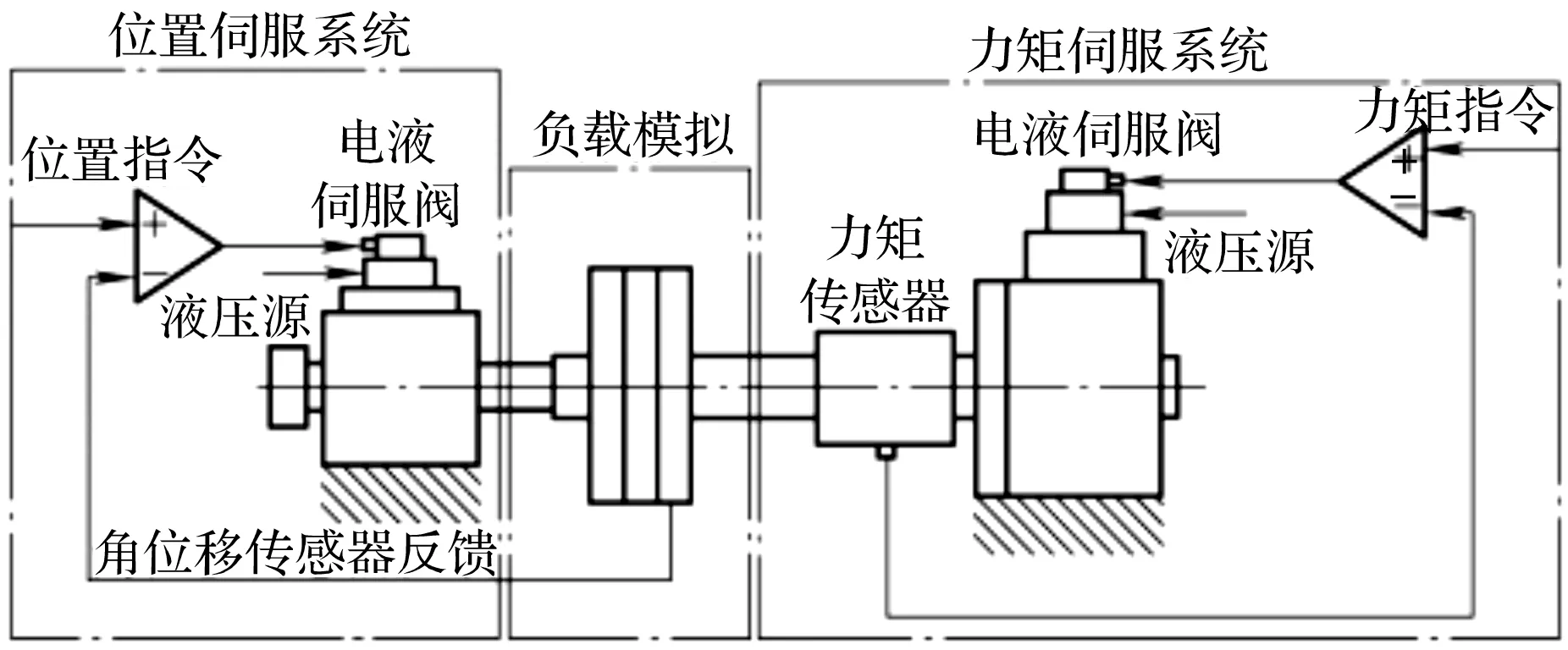
圖1 電液伺服加載系統試驗臺

由圖1可知:電液伺服閥通過驅動伺服馬達進行系統加載,加載試驗包括位置伺服和力矩伺服試驗。

此處的外負載擾動通過力矩伺服系統來提供。其中,力矩閉環時的力矩反饋通過與馬達軸固連的扭矩傳感器來完成,而位移反饋通過角位移傳感器來完成,控制算法系統由多個控制器來完成。

電液伺服加載系統試驗臺包括:1個油源、2個伺服閥、2個液壓馬達、2個力矩傳感器、2個位置傳感器,還包括工控機等測試系統。

電液伺服系統的主要參數如表1所示。

表1 電液伺服試驗臺系統主要參數

由于電液伺服系統動態模型的可靠性決定了系統的控制精度,為了抑制負載擾動,并實時預估非線性干擾的參數變化[2],此處的試驗臺采用了開環補償控制器和魯棒控制器的設計;同時,其與開環控制器并聯,筆者又增加了一個閉環PID控制器,以大大提高控制系統的靜態閉環精度,增加控制的穩定性。

1.2 數學模型

筆者參考圖1中的結構圖來建立電液伺服試驗臺各個部件的數學模型。其中,電液伺服閥的流量線性化方程為:

QL=KqXv-KcpL

(1)

式中:Xv—伺服閥的閥芯位移;QL—電液伺服閥送到液壓電機的負載流量;Kc—流量壓力系數;Kq—伺服閥的流量增益;pL—負載的壓力。

系統的力矩平衡方程為:

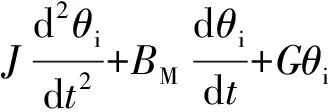
(2)

式中:M—系統的輸出力矩;θi—負載的等效角位移;J—負載的轉動慣量;G—負載的等效扭轉剛度;BM—負載的等效阻尼系數[3]。

對式(1,2)進行拉普拉斯變換可得:

Isv=Kiuc

(3)

QL=KqXv-KcpL

(4)

M=pLDM=Js2θi+BMsθi+Gθi=
Gs(θM-θi)

(5)

參照該電液伺服加載系統的工作原理,可以將其中的伺服閥化簡,變為一階慣性環節,即:

(6)

式中:Ksv—伺服閥的增益;Ts—伺服閥的時間常數[4]。

2 開環補償方法和位置伺服控制器模型

2.1 無擾動時的系統理論模型

假設電液伺服加載試驗臺系統無外界擾動時的理論模型為R(s),那么控制器Gθ(s)的設計就要考慮有外界擾動時的系統理論模型。

此處,控制器Gθ(s)實際上包括開環控制器和PID閉環控制器兩種類型,如圖2所示。

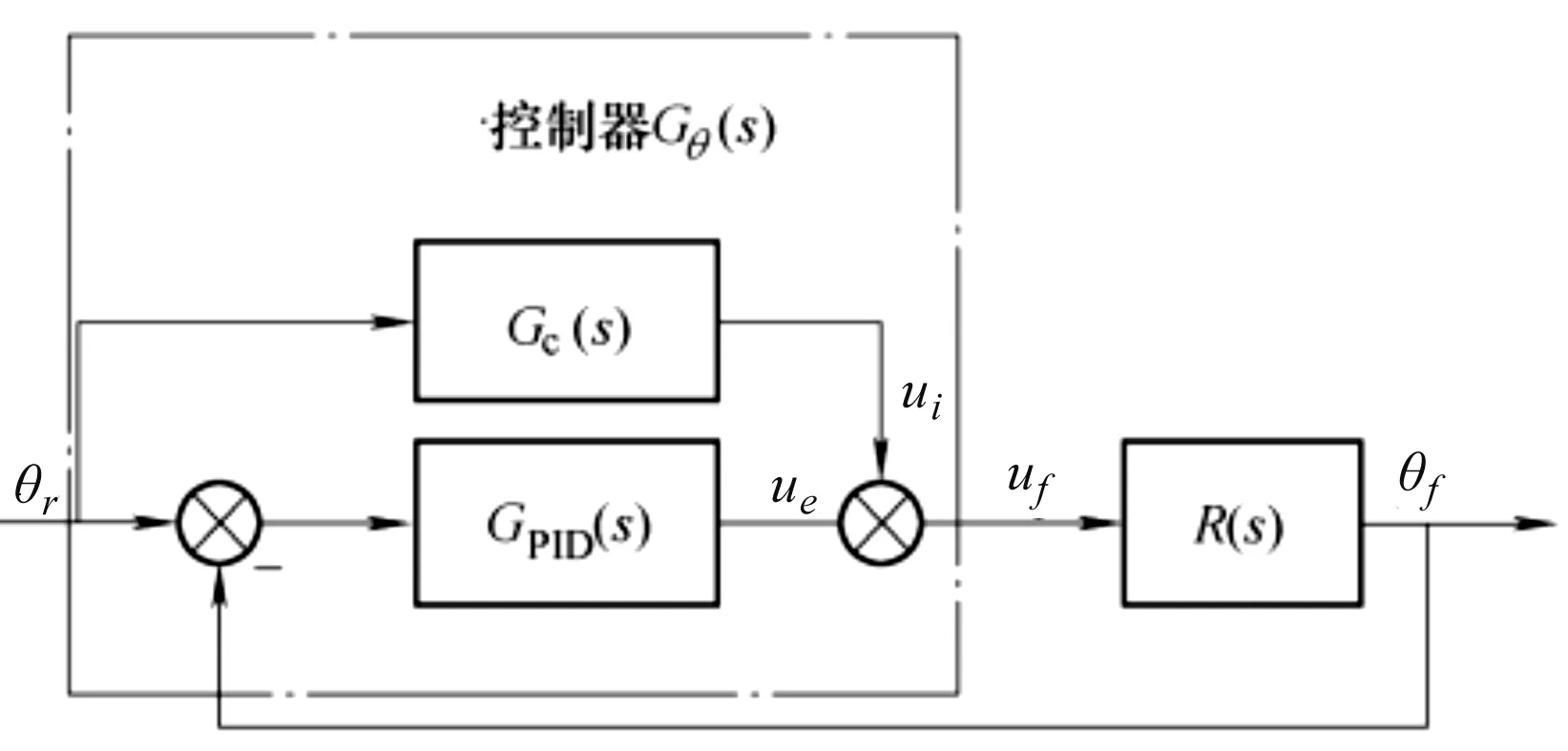
圖2 無擾動時的系統模型

由圖2可知,控制器Gθ(s)的控制輸出為:

uf=GPID(s)e(s)+Gc(s)θr

(7)

式中:Gc(s)—開環控制器。

開環控制器Gc(s)的表達式為:

(8)

因為在一個真實的系統中,并不能獲得絕對準確的理論模型R(s),所有理論模型及其模型辨識都只是一種近似的數學表達而已。

可以看出,開環控制器Gc(s)的表達式正是系統無擾動時的近似理論模型。另一方面,因為大部分模型分母的階次都大于分子的階次,一般系統模型都有很強的微分功能,這就可能增大噪聲干擾的作用,所以,該開環控制器的設計采用無擾動時的系統近似理論模型[5]。

2.2 開環補償控制方法

因為該電液伺服加載試驗臺對動態響應的要求較高,而伺服電機本身的數學模型簡單,控制性能也較好,因此,解決系統擾動的問題需考慮整體控制環路的設計。

因為負載的擾動會引起位置伺服系統的調整,這又會直接體現在伺服電機的調速作用上,所以關鍵是如何提高調速模塊抗擾動的能力。因此,位置伺服系統和調速系統都采用了自適應魯棒控制的方法[6]。

電液伺服加載試驗臺的系統參數有非線性的特點,外界的隨機擾動也會降低系統的控制精度和響應速度。為解決這個問題,筆者在位置伺服的開環控制中采用了一種依據期望軌跡規劃曲線進行速度補償的方法,期望軌跡規劃曲線圖如圖3所示。

圖3 期望軌跡規劃曲線圖

由圖3可知:依照實際的位置運動狀態、速度和方向,整個運動過程可分為加速段、勻速段和減速段3個階段,并可以計算出所需要運動段的特征角點[7]。

為了保證系統的穩態品質和高精度輸出,此處參照負載擾動引起的系統流量變化。這種位置開環補償控制方法是以期望軌跡規劃的速度作為一種中間控制變量,并去實時補償伺服電機的轉速數值。

該補償控制的數學模型為:

(9)

式中:ωm—伺服電機的轉速補償,rad/s;Vref—期望轉速,rad/s。

伺服電機的轉速補償需要根據調速模塊的參數調整來進行,這種速度開環補償方法對非線性和不確定的負載擾動具有一種自適應的特性,沒有必要提前去辨識擾動的特征[8]。

圖1中的電液伺服試驗臺系統中,其中的位置伺服系統在位置控制過程中,采用了一種開環補償的控制方法,根據位置輸出的偏差值進行閉環方式的反饋控制。

試驗臺的位置伺服系統及開環補償控制圖如圖4所示。

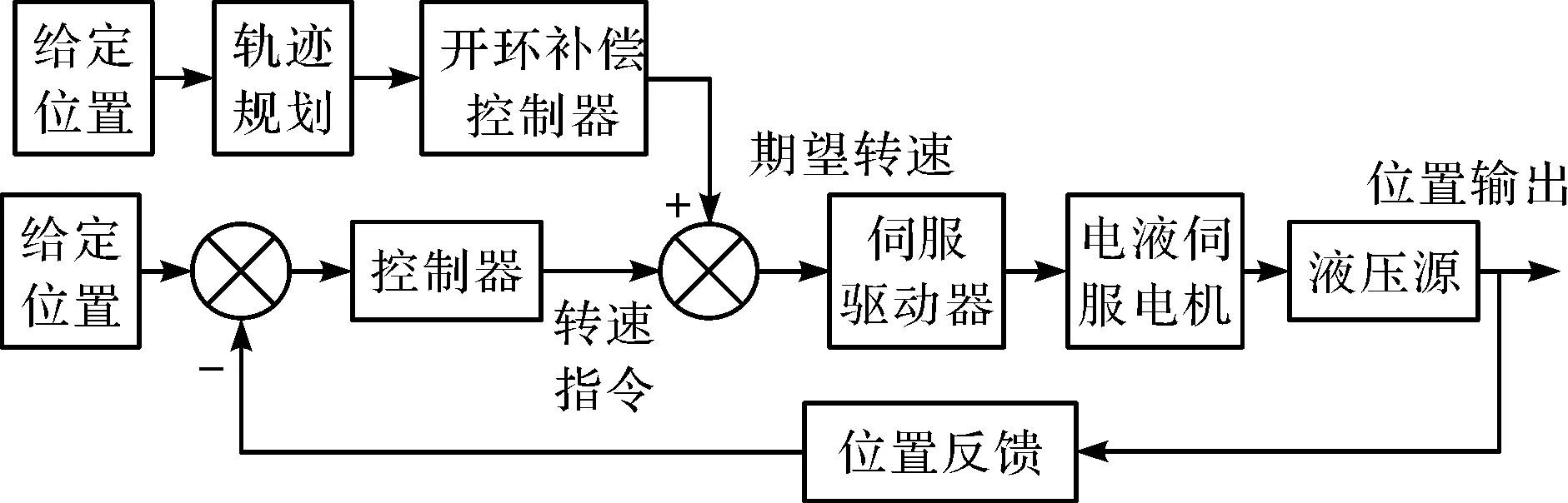
圖4 試驗臺位置伺服系統及開環補償控制圖

在系統位置開環補償的過程中,筆者參照上述試驗臺組成結構、試驗臺部件的數學模型,以及上述位置伺服開環補償原理,得出的伺服系統開環補償的傳遞函數圖如圖5所示[9]。

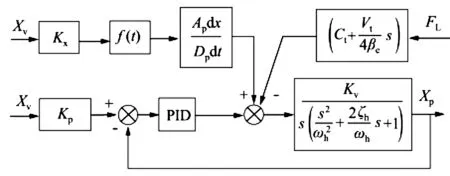
圖5 開環補償的傳遞函數圖

圖5中:由于系統中很多參數都具有隨機性的特點,采用單一的開環補償設計并不能完全滿足整個系統的控制精度要求。為了提升控制效果,還需要并聯設計一個經典的閉環PID控制器,以實現并行控制。控制器的參數可以采用臨界比例度法進行獲取。

閉環控制器可以對系統的位置進行基本的控制和調節;而開環補償控制器則根據位移來規劃系統的期望速度,以提高伺服系統的響應速度與控制精度為目標,準確地推算出伺服馬達轉速補償的基準值,送出實時動態的速度調整參數,準確校正和改變實際曲線運動的速度值,并縮短穩態誤差所用的時間[10]。

2.3 位置伺服控制器模型

該電液伺服加載試驗臺系統中,位置伺服的控制器的理論模型如圖6所示。

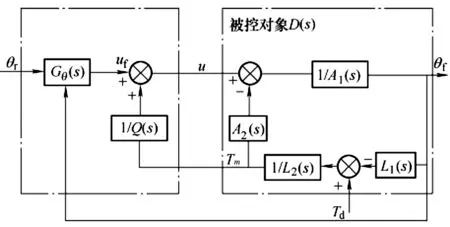
圖6 電液位置伺服控制器模型被控對象—圖4中的伺服驅動、伺服電機和液壓源部分;Gθ(s)—圖4中的位置控制器

圖6的電液位置伺服控制器模型體現了試驗臺中位置伺服系統的工作原理。

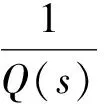
(10)

如果控制器Gθ(s)采用閉環方式,則有:

(11)

并且有:

(12)

(13)

式中:ψ—系統抑制外擾動的能力指數。

控制器Gθ(s)設計的主要任務是盡量優化控制系統的模型A1(s)。

3 自適應魯棒控制策略

在電液位置伺服加載試驗臺中,總壓力流量系數Ktm和伺服閥的流量增益Ku是系統工作運行時最主要的非線性參數,控制器的設計需要計算這些參數值。

系統中的技術參數包括靜態參數和動態參數兩種。其中,靜態參數通常是相對穩定的,而動態參數則是不確定的,并呈現非線性變化的特點。所以,為了穩定系統的技術性能指標,控制器的設計需要實時預估這些隨機的非線性參數,并優先采取自適應控制和魯棒控制的方法[12]。

在一般情況下,由于電液伺服閥具有比較寬的帶寬,其動態描述可為比例環節。由此,其負載流量的方程可以寫為:

qf=Kuu

(14)

(15)

(16)

其中:Kco可以由伺服閥空載的最大流量qo得出,即:

(17)

根據以上分析,可得該電液位置伺服加載系統的自適應魯棒控制模型,如圖7所示。

圖7 電液位置伺服系統自適應魯棒控制模型

由圖7可知:控制模型具備在線和實時預測伺服系統的非線性參數的功能,因此,可以設計具有自適應特性的魯棒控制器[13]。

4 電液伺服加載系統實驗

4.1 實驗條件

在電液伺服加載試驗臺中,為了驗證采用位置伺服開環補償魯棒控制策略的有效性,筆者進行系統加載試驗。

該試驗采用與PID閉環控制方式進行跟蹤曲線對比的方法。其中,系統測試的采樣周期設為0.5 ms;力矩伺服系統用來提供外負載干擾。

試驗臺數據測控系統由AD采集卡、DA輸出卡、計數器等組成;采用IEIWS-855GS工控機及相關程序進行數據的實時采集;位置指令信號通過相應的控制算法產生,驅動信號由信號調理電路和放大電路輸出,控制電液伺服閥的運動。

4.2 位置跟蹤實驗(跟蹤頻率3 Hz)

在進行電液伺服系統性能加載對比試驗時,筆者設定開環補償魯棒控制和PID閉環控制的已知參數相同。

在兩種控制方式下,系統抗擾動的實驗結果以及對比曲線,如圖8所示[14]。

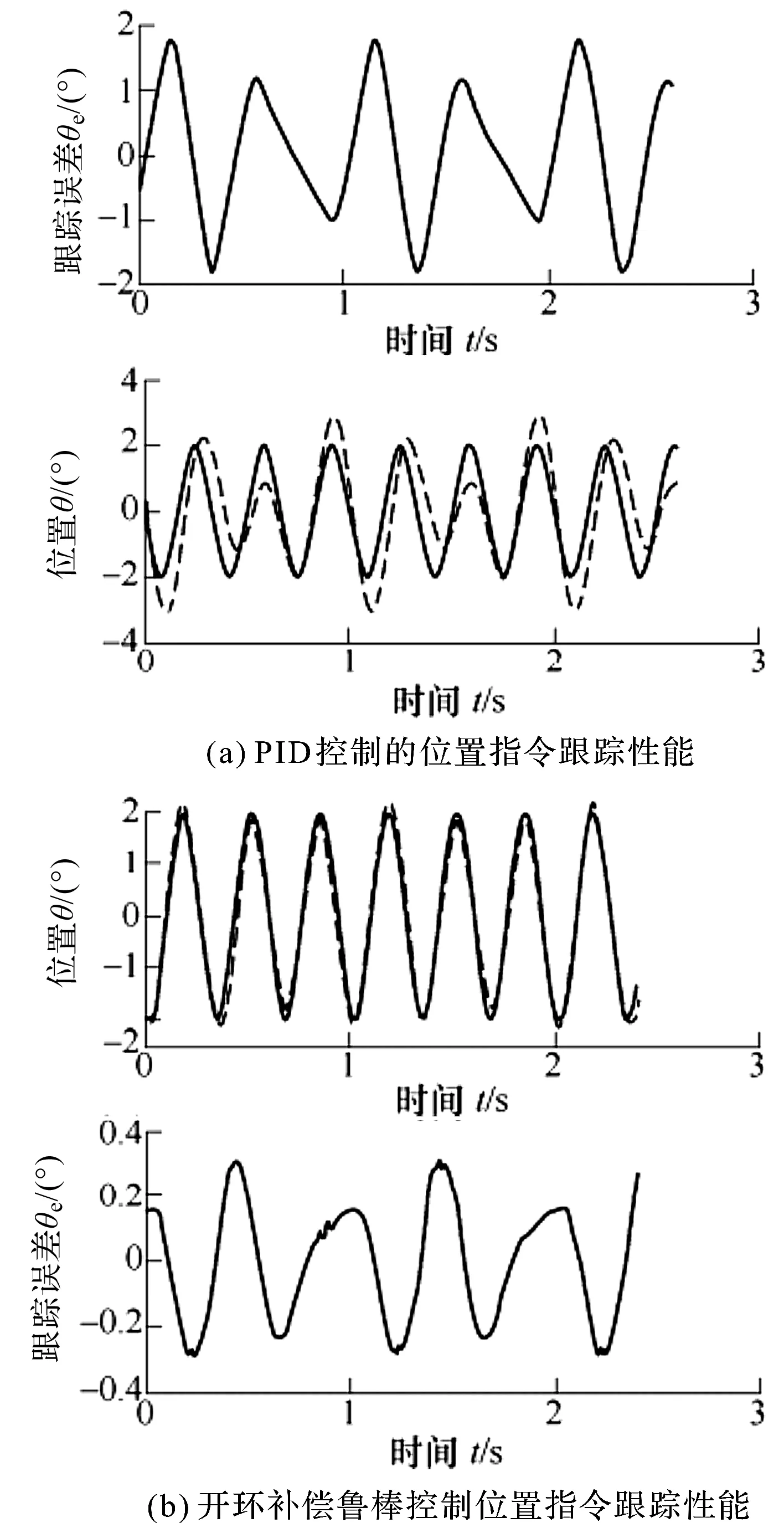
圖8 電液伺服位置跟蹤實驗曲線比較(跟蹤頻率3 Hz)位置圖中：實線—位置指令曲線;虛線—跟蹤曲線

從圖8可以看出:當電液位置伺服系統跟蹤頻率為3 Hz、幅值為2°的正弦波,系統實施加載力矩為1 000 N·m、加載頻率為2 Hz的正弦干擾力矩時,如果采用PID閉環控制方式,擾動下的跟蹤曲線顯示已經無法實現位置指令的正常跟蹤;如果采用開環補償的魯棒控制方式,伺服系統的位置跟蹤能較成功地抑制非線性擾動因素,系統魯棒性強,跟蹤曲線的跟蹤效果十分明顯。

4.3 位置跟蹤實驗(跟蹤頻率20 Hz)

如果系統跟蹤頻率為20 Hz的正弦波時,其實驗結果的對比特性曲線如圖9所示。

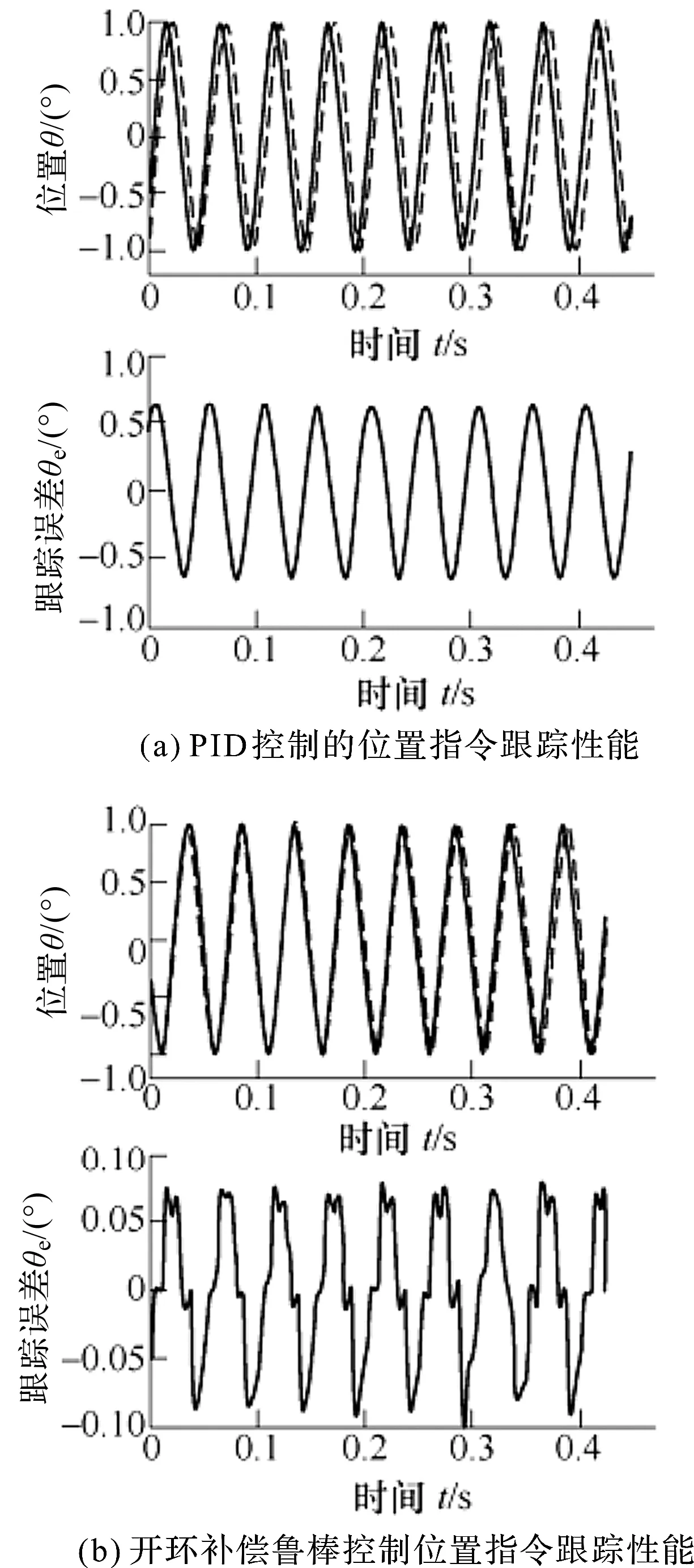
圖9 電液伺服位置跟蹤實驗曲線比較(跟蹤頻率:20 Hz)位置圖中:實線—位置指令曲線;虛線—跟蹤曲線

圖9中,當位置跟蹤頻率為20 Hz、幅值為1°的正弦波時,PID閉環控制方式存在一定的相位滯后現象,跟蹤誤差偏大,甚至超過了位置指令幅值的50%,可知高頻下的位置跟蹤性能較差;而采用開環補償魯棒控制方式的跟蹤誤差就很小,僅約占位置指令幅值的15%左右,因此,高頻下位置跟蹤性能較好。

4.4 系統“雙十”頻寬特性分析

該電液位置伺服系統的“雙十”頻寬是衡量系統頻率響應的一個重要指標,即其頻率響應曲線中能夠同時滿足輸出幅值的衰減小于10%以及相位滯后10°的頻率,這比一般伺服系統的-3 dB頻寬和-90°相移頻寬指標要嚴格得多。

在該試驗中,用BT1250頻率特性儀給電液位置伺服系統輸入幅值為1°,同時頻率逐漸增加的正弦信號,進行開環掃頻,測量系統的開環頻率響應,實驗結果如圖10所示。

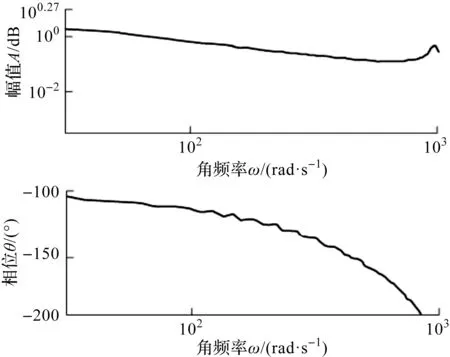
圖10 系統開環頻率響應圖

一般伺服系統的-3 dB頻寬都小于100 Hz,“雙十”頻寬基本小于30 Hz。從圖10可以看出:在實驗頻率范圍以內,該電液伺服系統大部分具有一階環節的串聯積分環節的特點,只有到了高頻部分,才表現出更高階次的一種模態。

實驗結果表明:當位置跟蹤頻率為20 Hz、幅值為1°的正弦波時,在PID閉環策略下,系統的“雙十”帶寬只有6 Hz;而在開環補償魯棒控制方式下,系統的“雙十”帶寬可擴展到22 Hz[15]。

4.5 結果分析

筆者所提出的電液位置伺服開環補償與魯棒控制策略是基于系統模型的。由上述試驗結果可以看出,位置跟蹤誤差小,低頻和高頻下跟蹤性能均較好。

試驗結果的主要理論依據是系統模型和參數預估策略是正確和有效的。由圖7的系統模型可知,伺服控制器的總輸出可根據系統參數和輸出進行反推演算而得出。試驗中,當位置跟蹤頻率為3 Hz、幅值為2°的正弦波,系統實施加載力矩為1 000 N·m、加載頻率為2 Hz的正弦干擾力矩時,反推演算出的輸出值特別接近位置伺服系統實際控制輸出的值,誤差大約只有0.1 V～0.2 V,這個誤差只有系統最大輸出值的約3%左右[16]。

由此可見,上述系統模型和在線參數預估的策略是合理和有效的。

5 結束語

針對電液伺服加載系統存在的負載擾動和非線性干擾問題,筆者提出了一種電液位置伺服加載系統的開環補償與魯棒控制解決方案;搭建了一套較為完整的電液伺服加載試驗臺系統,建立了試驗臺系統的數學模型,提出了抑制擾動的開環補償方法,對期望軌跡規劃的位置開環補償控制方法進行了分析,對位置伺服控制器的模型進行論證。

為提高系統的動態響應品質,減小系統位置伺服的控制誤差,通過運用并聯PID閉環控制的復合型控制措施,實時校正實際運動曲線的速度值,在線預估伺服系統的非線性參數,并不需要對擾動的特性進行事先辨識;最后,筆者進行了位置伺服的加載實驗。

研究結果表明:

(1)開環補償和魯棒控制策略的位置跟蹤性能優良,跟蹤曲線控制精度高;當跟蹤頻率為20 Hz時,跟蹤誤差只有位置指令幅值的15%左右;

(2)當位置跟蹤頻率為20 Hz時,開環補償和魯棒控制策略下,系統的“雙十”頻寬可擴展到22 Hz,頻寬特性好;

(3)開環補償與魯棒控制策略可以明顯增強電液伺服系統抗外界非線性擾動的能力,位置控制器的自適應能力大大優于傳統閉環控制方式的電液伺服系統。

在該系統后續的研究工作中,筆者將加強對外部擾動因素進行量化分析和判斷,從而進一步提升位置伺服系統跟蹤的準確度,擴展“雙十”頻寬。