Gorenstein內射Phantom態射①
王小妹,王占平
西北師范大學 數學與統計學院,蘭州 730070
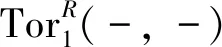
受以上結論的啟發,本文主要研究Gorenstein內射Phantom態射.
1 預備知識
本文中所提到的環均指有單位元的結合環,模均指左R-模.R-Mod(Mod-R)表示左(右)R-模范疇.
定義1用H(R)表示R-Mod的態射范疇,其中:
(a)H(R)中的對象是左R-模同態;
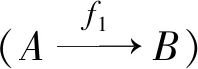
使得圖
交換.
由文獻[12]可得,態射范疇H(R)是局部有限表示的Grothendieck范疇.
2 Gorenstein內射Phantom態射
文獻[13]在一般環上引入了Gorenstein內射模的概念.

Gorenstein內射模的類記為ΓI.
由此我們引入Gorenstein內射Phantom態射的概念.
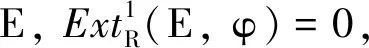

命題1在H(R)中,ΓI-Phantom態射的類關于直積封閉.

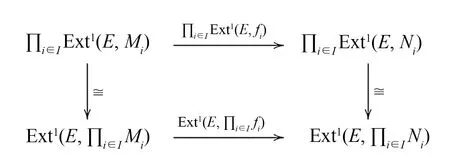


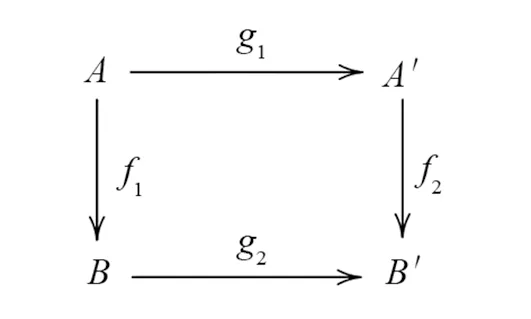
證對任意的內射左R-模E,考慮交換圖
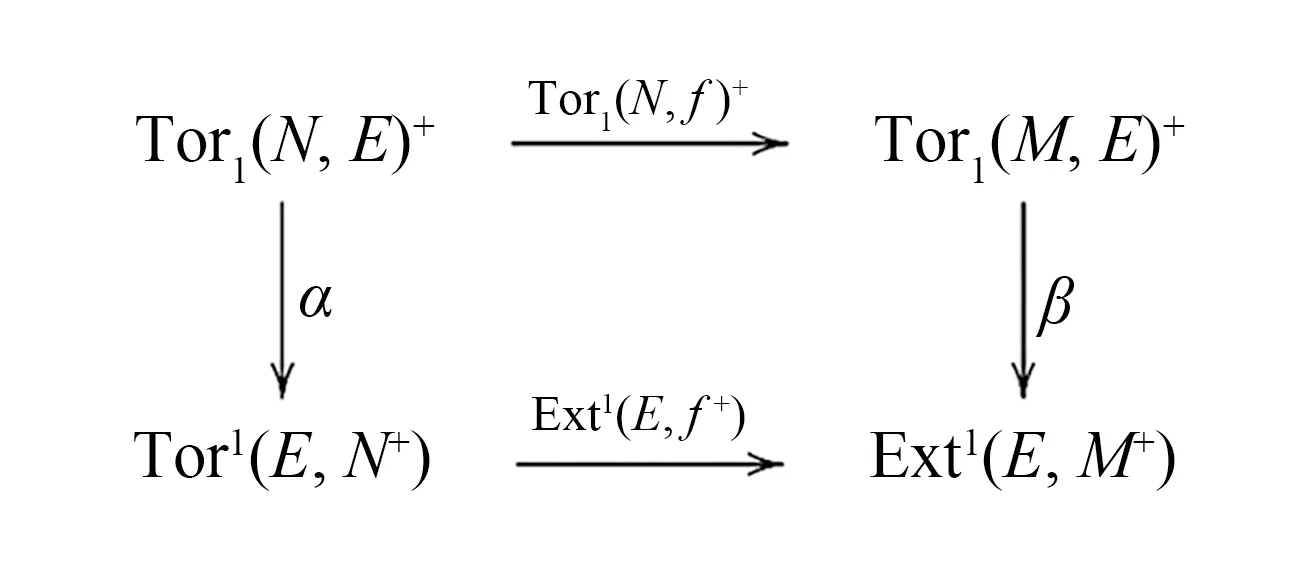


(i)φ是ΓI-Phantom態射;

是HomR(E,-)-正合的.

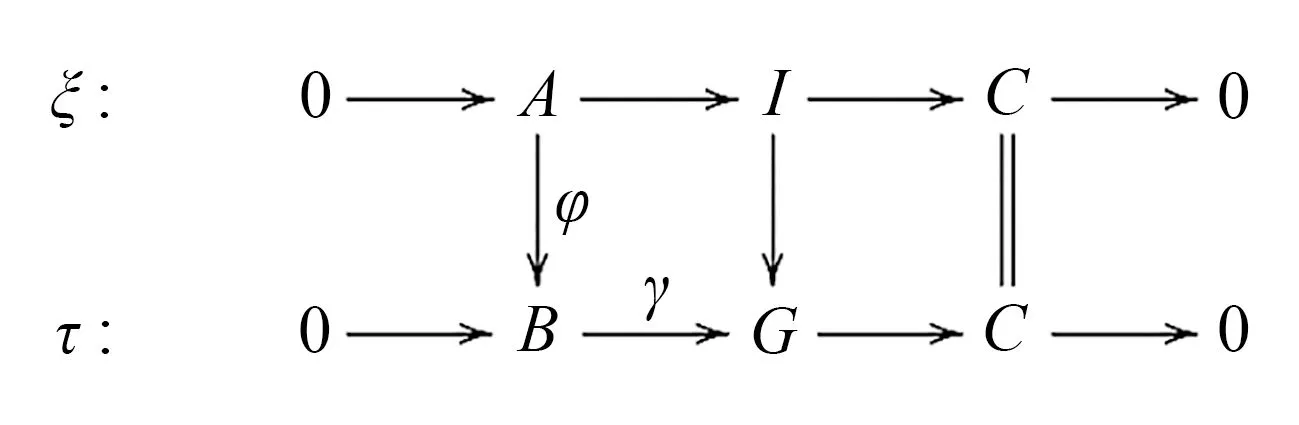

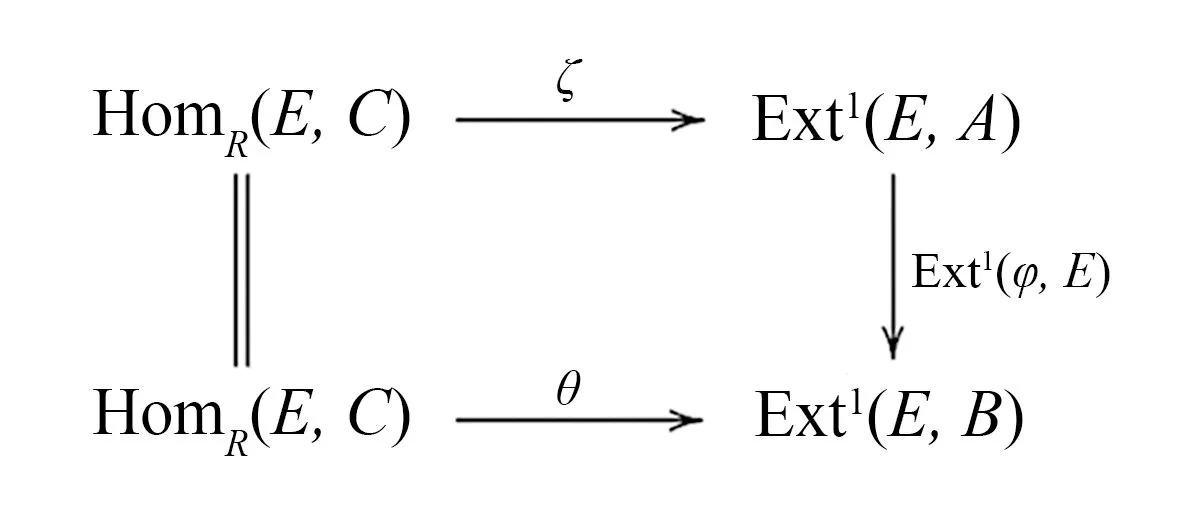
(ii)?(i)假設(ii)成立,則對任意的內射左R-模E,考慮交換圖
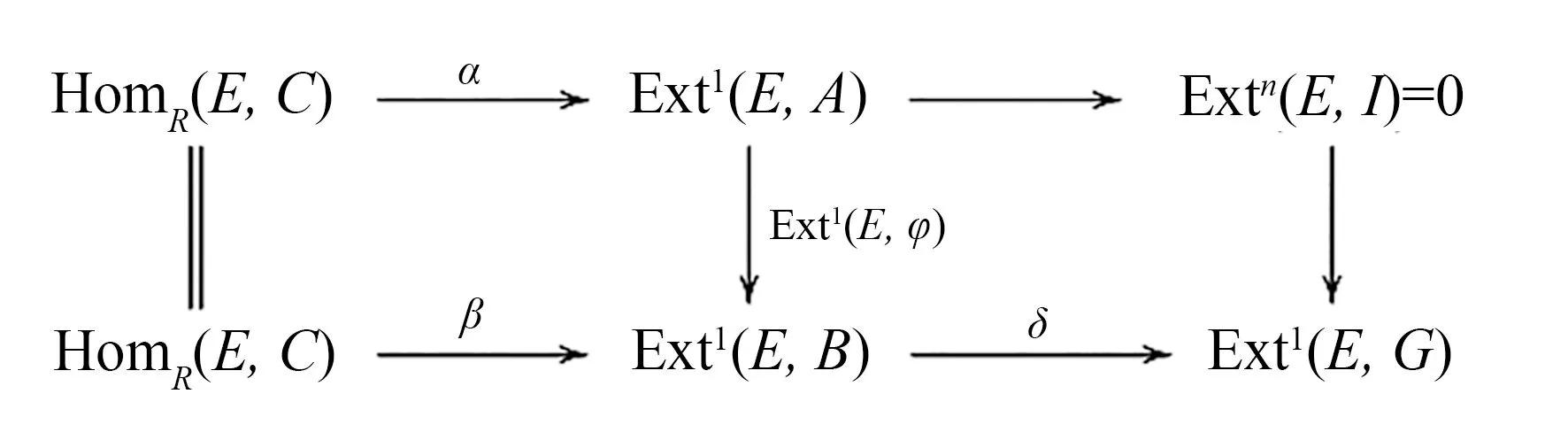
有δExt1(E,φ)=0. 因為δ是單的,所以Ext1(E,φ)=0,即φ是ΓI-Phantom態射.
3 高維Gorenstein內射Phantom態射
下面引入高維Gorenstein內射Phantom態射的概念,即n-Gorenstein內射Phantom態射(n∈N+).
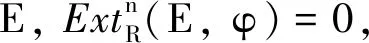
n-ΓI-Phantom態射的類記為Φn-ΓI.
注1當n=1時,1-ΓI-Phantom態射就叫作Gorenstein內射Phantom態射,即ΓI-Phantom態射.
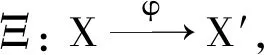
(i)φ是n-ΓI-Phantom態射;




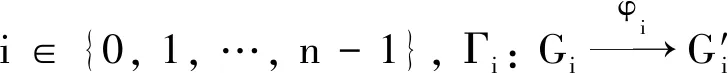
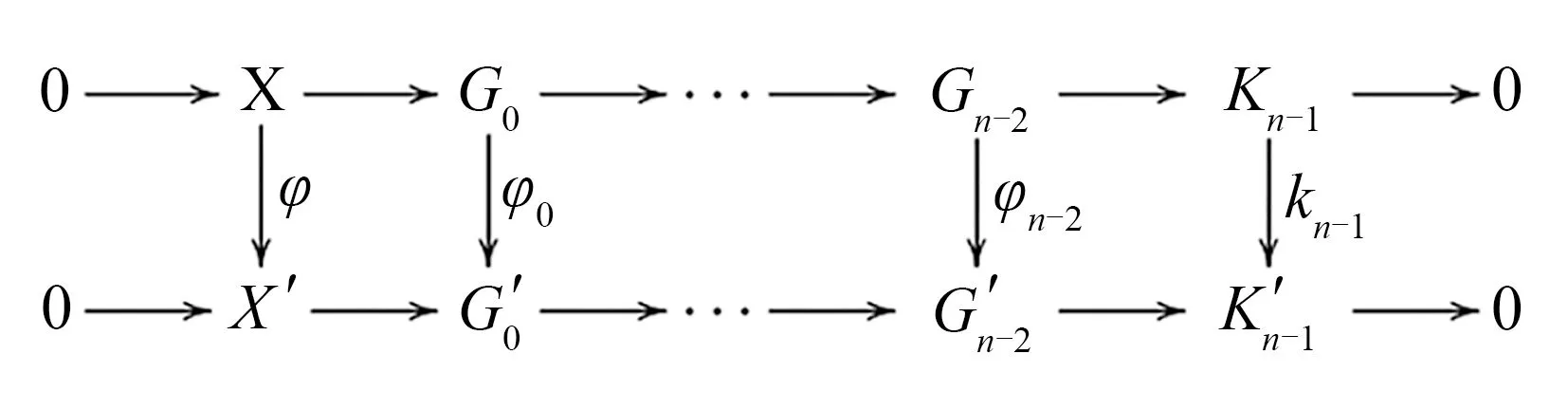

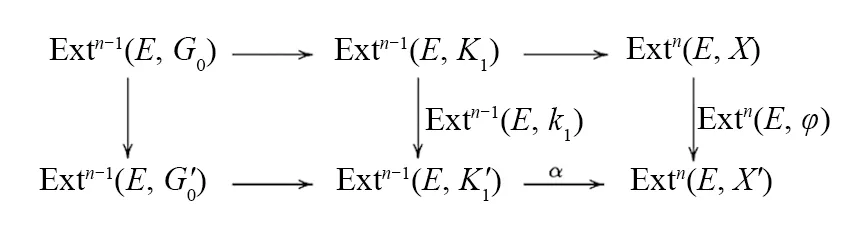
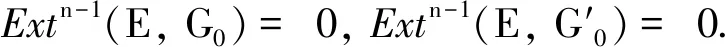
(ii)?(iii)?(iv)?(v)顯然.
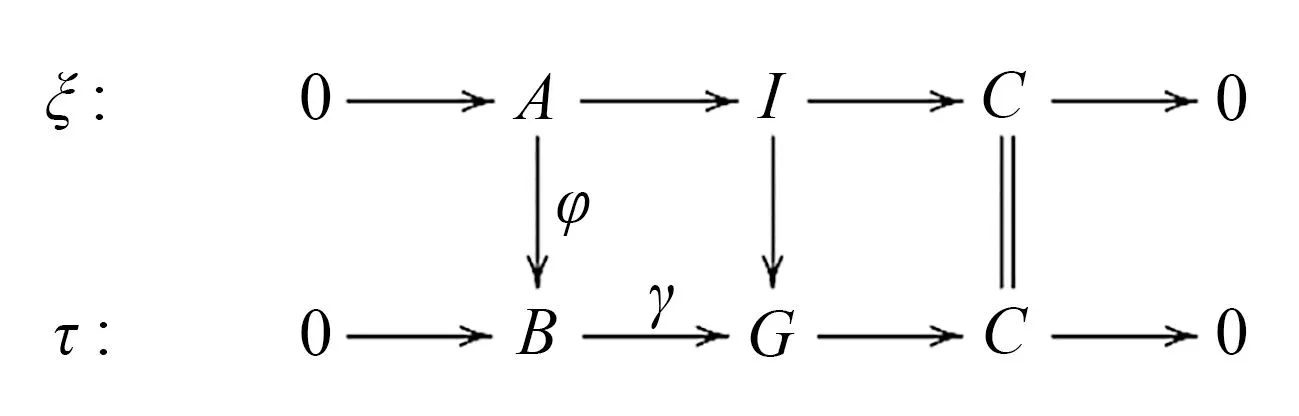
(v)? (i)考慮行正合的交換圖
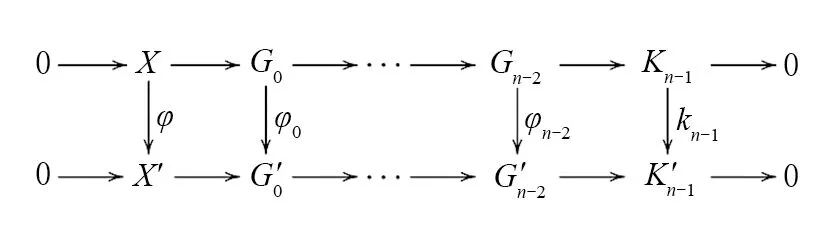

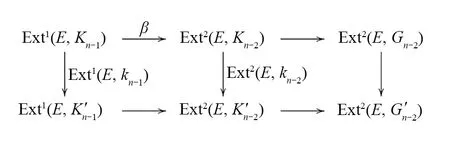
因為φn-2是Gorenstein內射態射,所以Gn-2,G′n-2是Gorenstein內射模,即Ext2(E,Gn-2)=0,Ext2(E,G′n-2)=0. 則β是滿射,所以Ext2(E,kn-2)β=0. Ext2(E,kn-2)=0. 重復上述過程,有Extn(E,φ)=0. 所以φ是n-ΓI-Phantom態射.

