基于變分模態分解的結構裂紋識別*

楊啟航， 李林安， 李利青， 米少瑄

（天津大學 機械工程學院，天津 300354）

引 言

我國經濟建設的發展不斷加快，城鄉交通需求逐步增長，因而各式各樣的橋梁也相繼建成.與此同時，橋梁受到材料老化、過載、侵蝕和地震等因素不同程度的破壞，導致橋梁的承載能力、安全性和耐久性都在不斷削弱.經過大量研究人員多年的不懈努力，提出了多種不同的橋梁結構檢測方法.

總的來說，可以將橋梁結構檢測方法分為基于完整有限元模型和不基于完整有限元模型的方法[1].前者主要面臨的困難是獲取準確完整的模型，然而一些舊橋已經使用了很多年，甚至連圖紙都丟失了，這是根本無法實現的.后者沒有這個問題，而是依賴于可靠的結構響應和先進的信號處理方法.

近年來，信號處理技術得到了不斷的發展，不基于完整模型的方法得到了越來越多的研究，其中最常用的就是小波分析.Zhu 和Law[2]提出了一種基于小波分析的簡支梁響應多尺度分解的裂紋識別方法，并通過仿真和實驗進行了驗證.在隨后的研究中，為了檢測多裂紋梁的識別效果，劉光耀等[3]利用小波分析與變異系數的結合，構建了新型檢測指標，檢測過程擺脫了對完好結構信息的依賴.Khorram 等[4]根據小波變換的局部極值，定義了一種移動荷載作用下的裂紋梁損傷指數，該指數可以檢測到梁高10%以上的小裂紋.雖然理論上，小波分析可以分析非線性非平穩復雜信號[5]，然而各種問題也在實際應用中出現，最突出的是小波分析的結果對初始基函數極為敏感.因此，初始基函數選擇不同，將會帶來巨大誤差.對此，經驗模態分解(EMD)[6]避免了小波變換的不足且得到了廣泛使用.Meredith 等[7]通過對橋梁在車輛荷載作用下的加速度響應分析，驗證了該方法可以檢測出單損傷和多損傷.此外，以EMD 為基礎的Hilbert-Huang 變換(HHT)，廣泛應用于工程信號處理.Roveri 和Carcaterra[8]研究了使用基于HHT 的方法對受損橋梁進行損傷檢測的可行性，并在沒有與未損壞結構的響應進行比較的情況下識別出了橋梁上的損傷位置.然而，EMD 沒有嚴謹的理論基礎，模態混疊、端點效應以及計算效率低等問題時常出現在應用過程中[9].雖然有很多學者針對EMD 的缺點進行了研究[10]，但并沒有從根本上解決.21 世紀初，變分模態分解(VMD)[11]在EMD 的基礎上被提出，其原理不同于小波分析和Fourier 變換.VMD 保留了EMD 的優勢，同時也克服了EMD 在迭代過程中出現的諸多問題.目前，VMD 在機械故障診斷中應用得最為廣泛[12-14]，但在土木工程領域應用甚少.Bagheri 等[15]分別應用人工神經網絡和VMD，根據建立的模態頻率與抗彎剛度之間的關系來確定橋梁的抗彎剛度.結果表明該方法能夠在沒有完整結構信息的情況下，預測橋梁的抗彎剛度.王超等[16]將VMD 和廣義Morse 小波聯合使用，得到了框架結構的瞬時頻率.Mousavi 等[17]應用VMD 對受損橋梁的加速響應進行分解，并構造了新的損傷識別指標，成功地識別出了損傷存在的位置.據此，VMD 在橋梁損傷檢測領域存在良好的應用前景.

本文提出的方法是一種不基于完整有限元模型的裂紋檢測方法，且該方法僅需在跨中布置一個加速度傳感器，減少了在實際工程中傳感器的裝卸以及維護工作.首先，本文推導出了在移動荷載作用下，帶裂紋簡支梁跨中位置處加速度的解析表達式.其次，在有限元模擬環境下，進一步建立了車輪荷載作用下的簡支裂紋梁模型，并提取了跨中位置處的加速度響應.對加速度響應進行VMD，得到了含有損傷信息的模態，然后經過Hilbert變換得到了相應的瞬時頻率和瞬時能量.同時，利用對損傷敏感的瞬時頻率對裂紋存在的位置進行識別，可以識別出裂紋深度占比 δ在10%以下的小裂紋.構造了對裂紋深度敏感的指標來評估裂紋深度.最后，驗證了該方法在不同的輪載大小、噪聲程度以及裂紋數量條件下的有效性.

1 VMD

2 損傷指標的構建

3 移動荷載作用下裂紋梁動力分析

現如今，跨徑在5 ～20 m的小跨徑橋梁中，簡支板橋得到了廣泛的應用.工程上，通常規定裝配式板橋的跨徑為 8 ～16 m， 每塊預制板的寬度在1 .0 ～1.4 m 之 間，板厚約為 0.16 ～0.36 m. 因此，假設梁長L=15 m，寬度B=1.2 m ， 高度H=0.3 m.在移動荷載作用下，該類型橋梁的裂紋損傷識別可簡化為如圖1 所示的模型.

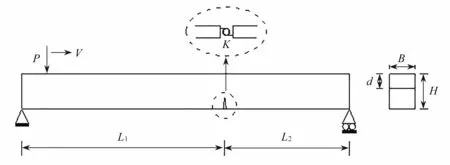
圖1 移動荷載下的裂紋梁模型Fig. 1 A cracked beam model under a moving load

圖3 給出了簡支梁跨中位置處豎向位移響應的有限元模擬結果.為了便于結果的觀察，模擬結果圖的橫坐標均采用了歸一化的移動荷載位置x?=x/L， 在勻速情況下，等于歸一化時間t?=t/T，下文均采用此方式.圖3中的位移信號可以看作為兩個正弦信號的疊加，高頻部分在移動荷載達到裂紋位置處幅值有所增大.相位差在圖中表現得不夠明顯，但其依然存在.所以，其結果基本符合上述理論推導.

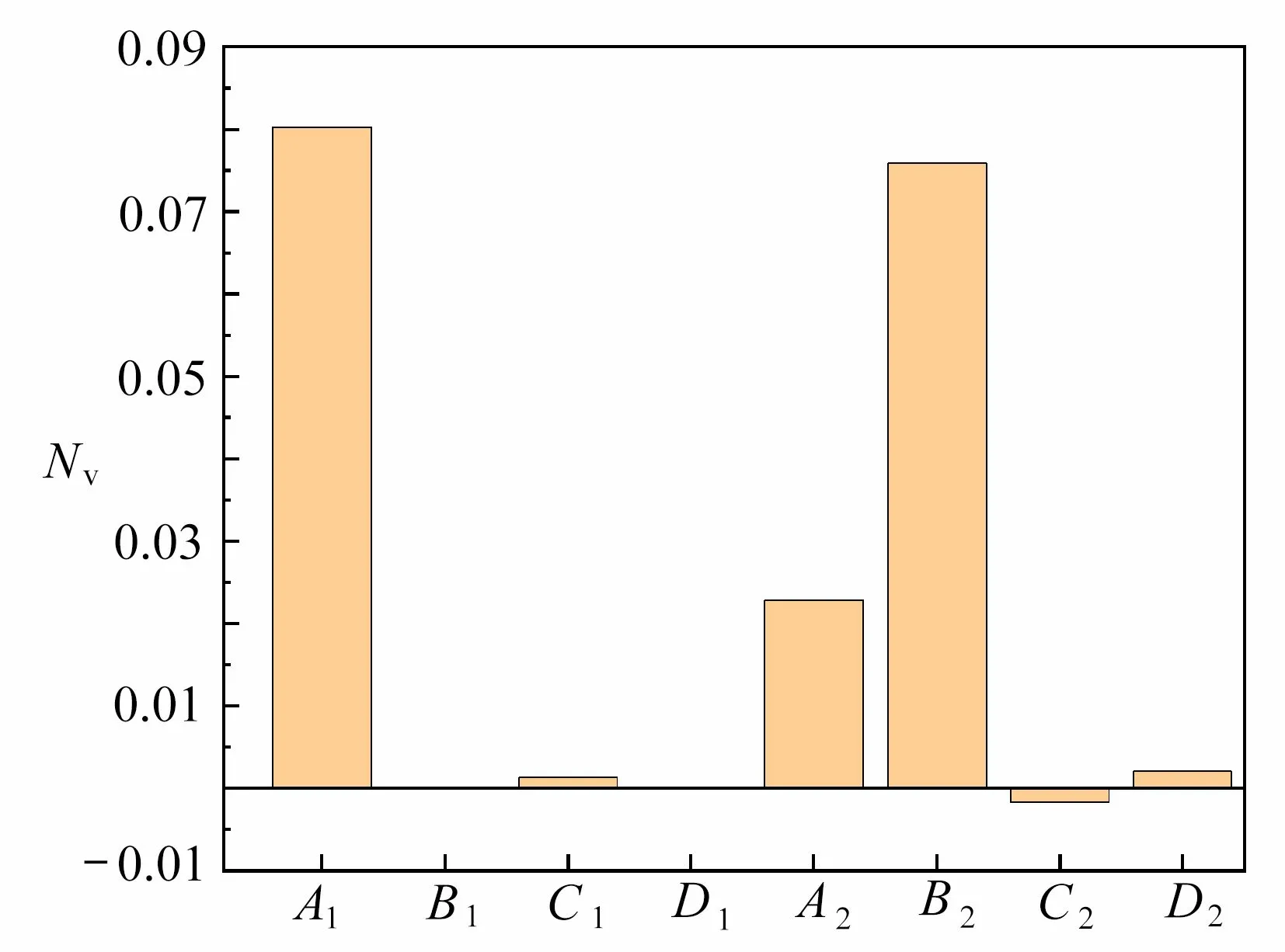
圖2 積分常數Fig. 2 Integration constants

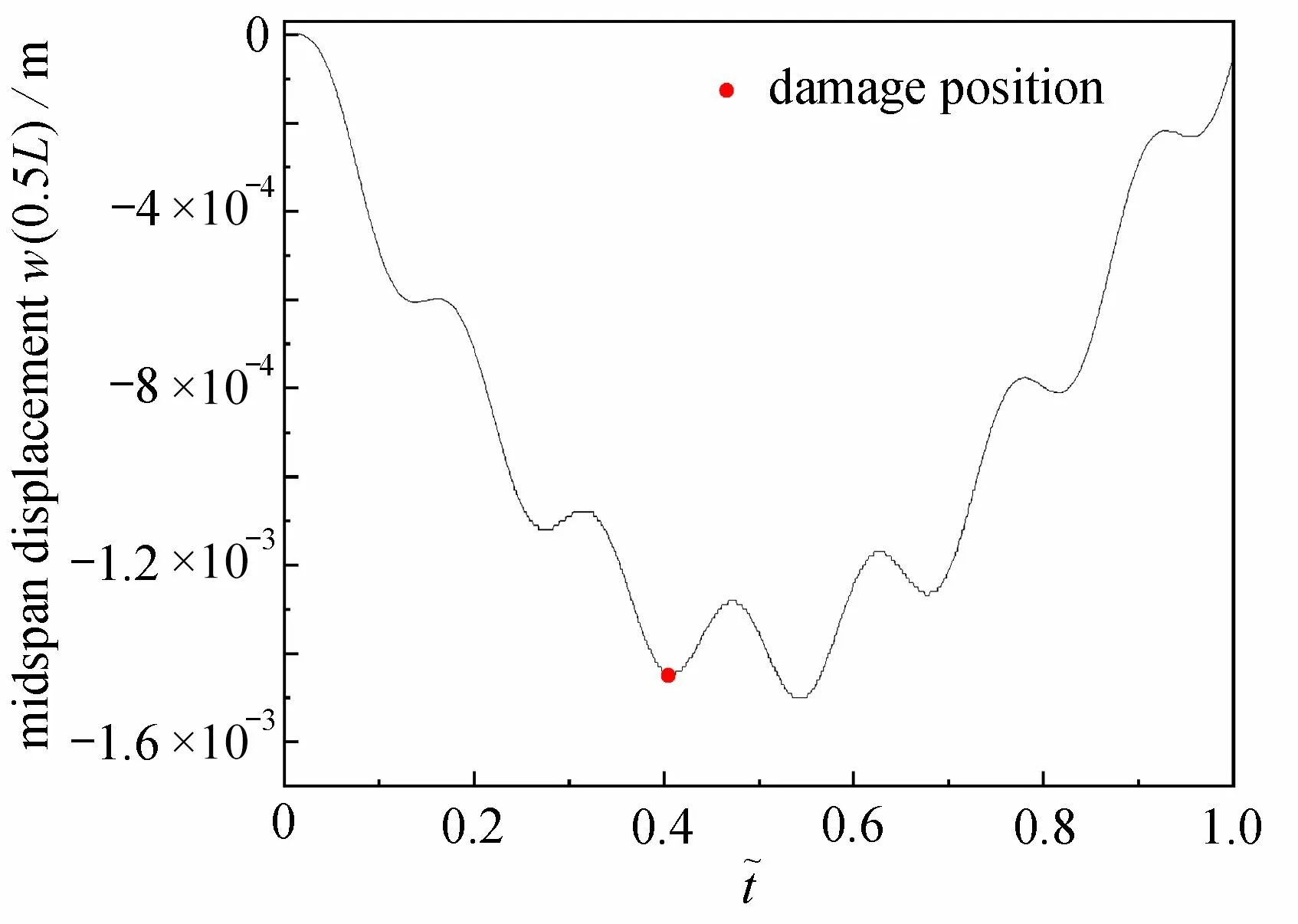
圖3 跨中位移Fig. 3 The midspan displacement

有限元模擬的結果如圖4 所示，跨中加速度響應可以認為是基頻正弦部分和高頻信息的疊加.同時，高頻信息是由指數項(t)滋生的.由于高頻信息的存在，圖中不能很好地表現相位差，但其仍然存在.因此，其結果與推導結果基本吻合.由于裂紋的存在，導致移動荷載經過裂紋位置后，使其跨中加速度響應出現了幅值和相位的變化.本文所提出的方法正是利用了這些突變去識別裂紋損傷.

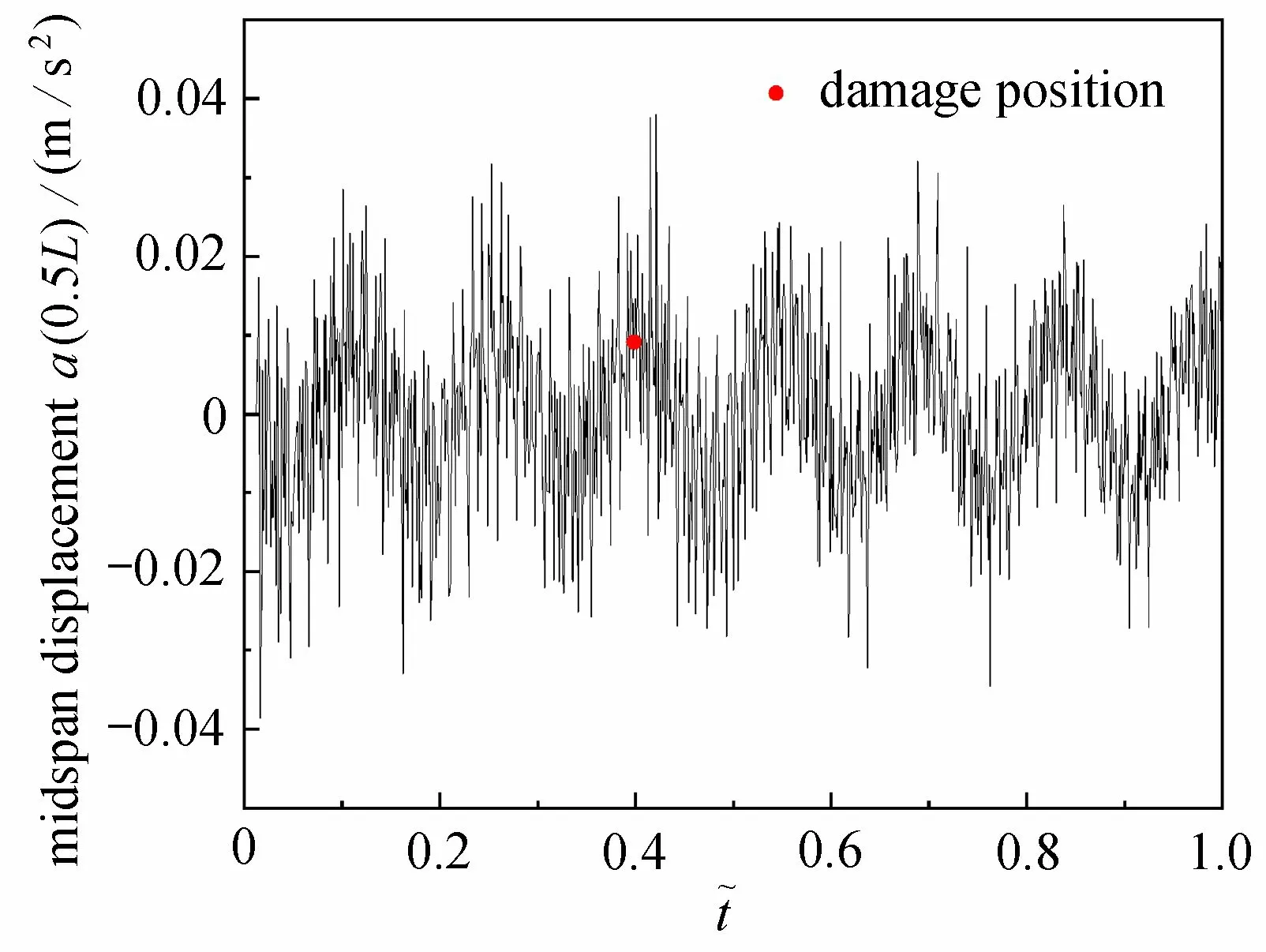
圖4 跨中加速度Fig. 4 The midspan acceleration

4 數 值 算 例

事實上，車輪在路面運動過程中，與路面有一定的接觸面積.為進一步貼切車輪作用在橋面的實際效果，本文將圖5（a）所示的移動集中荷載P轉換為圖5（b）所示的非均布荷載.根據王揚[19]的研究，將該非均布荷載簡化為二次拋物線的形式.一般車輛靜態時，輪胎與路面的接觸長度為r=10 ～30 cm；由于車輛移動過程中，輪胎變形不充分，須進行一定的折減.本文取r=20 cm，且考慮折減系數為0.8，則實際接觸長度為r×0.8=16 cm. 數值模擬的采樣時間為1 2 s.其他相關參數均列于表1.

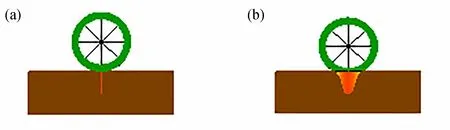
圖5 車輪荷載：（a） 集中荷載；（b） 非均布荷載Fig. 5 The wheel load: (a) a concentrated load; (b) an ununiform load

表1 模擬工況Table 1 The simulation condition

4.1 損傷位置分析

對提取的跨中加速度信號進行VMD.VMD 方法的性能取決于輸入參數，其中包括懲罰系數α、模態個數k等參數.本文取α =18 000，k=5，其他參數按照默認取值，即可滿足工況一的需求.分解結果如圖6 所示.

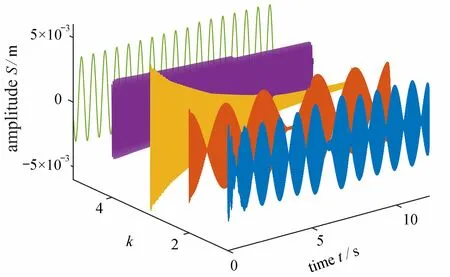
圖6 VMDFig. 6 The VMD

由圖6 可知，VMD 將加速度分解為5 個IMF 分量.在得到的瞬時頻率中，發現IMF 4 分量的瞬時頻率圖能夠準確地顯示出工況1 的裂紋位置，結果示于圖7.同時，當輪載通過裂紋位置后，可以看出瞬時頻率幅值出現了一定的波動.由圖8 可知，IMF 5 分量的瞬時能量波動范圍的均值在裂紋位置處有明顯的提升，且IMF 5 所對應的頻率正是式（29）中的基頻部分.根據這兩種現象可知，VMD 將裂紋損傷帶來的相位和幅值的突變，分別儲存在了IMF 4 和IMF 5 兩個分量中.然而根據式（29），裂紋損傷帶來的相位和幅值的突變應該都在IMF 5 中，這可能受到了滋生高頻部分的影響導致VMD 過程中出現了誤差，致使相位突變包含到了IMF 4 中.相比于瞬時能量，瞬時頻率對裂紋位置的識別更加準確.

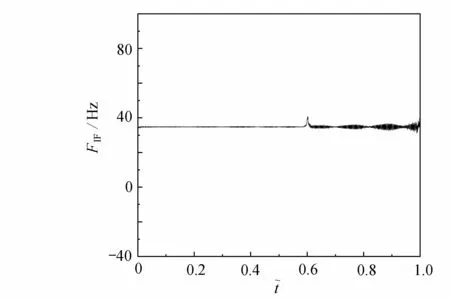
圖7 IMF 4 瞬時頻率Fig. 7 The IMF 4 instantaneous frequency

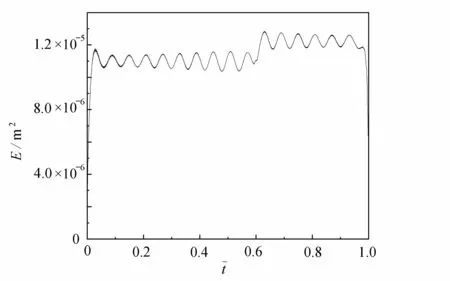
圖8 IMF 5 瞬時能量Fig. 8 The IMF 5 instantaneous energy

4.2 損傷程度分析

研究人員對橋梁進行損傷檢測時，一直都很關注檢測手段能否對受損橋梁做出良好的損傷程度判斷，這對橋梁剩余使用壽命的預測是非常關鍵的.本文對裂縫深度占比δ 分 別為 2 0%，1 5%，1 0%和 5%四種情況進行損傷程度的判斷，其他條件與工況1 相同.其瞬時頻率和瞬時能量圖分別如圖9、圖10 所示.

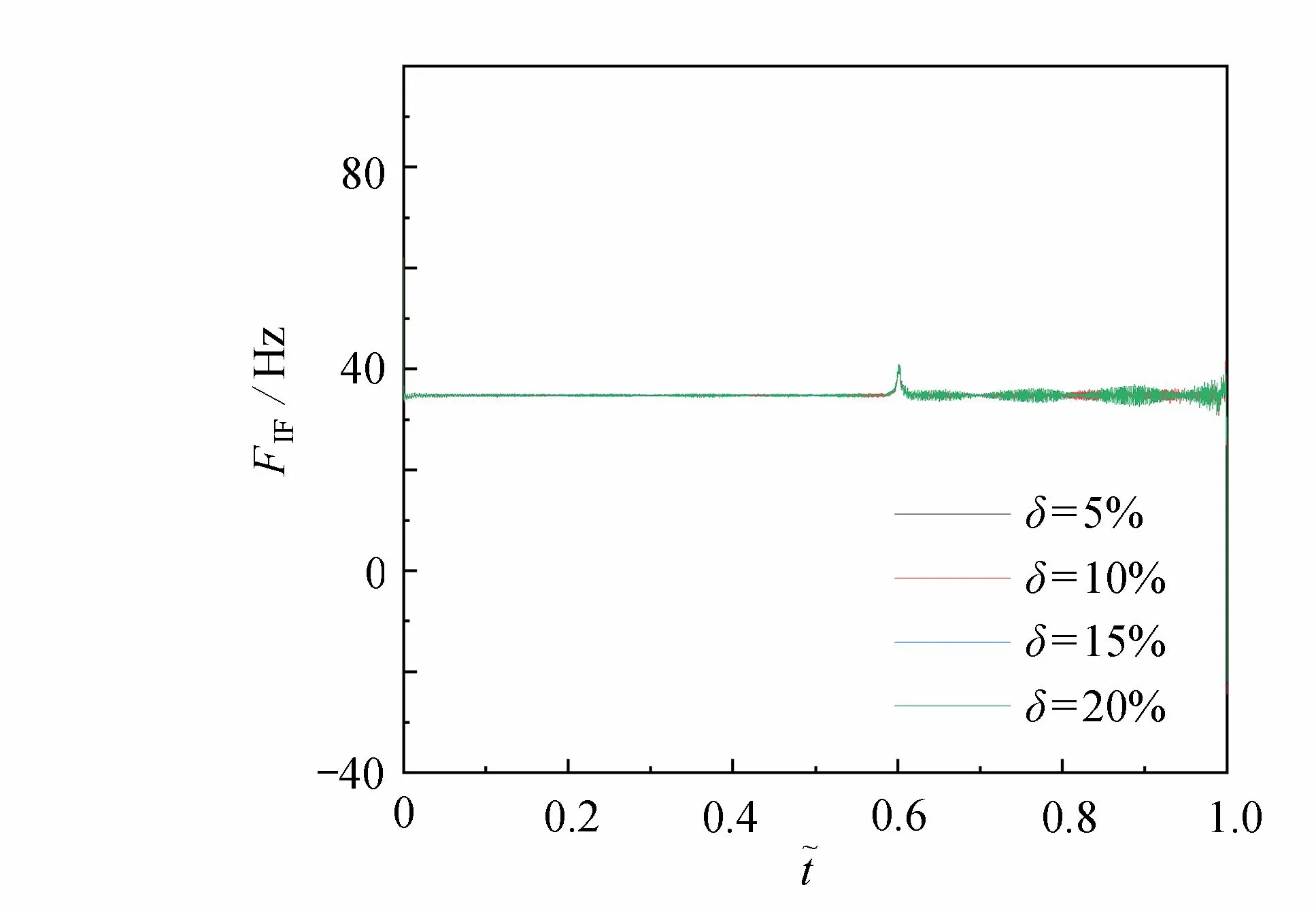
圖9 δ 為 20 % ，15% ，1 0% ，5% 的瞬時頻率對比Fig. 9 Comparison of instantaneous frequencies for δ= 20%, 15%, 10%, 5%

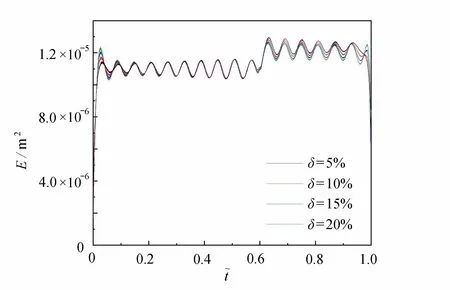
圖10 δ為2 0% ，15% ，1 0% ，5% 的瞬時能量對比Fig. 10 Comparison of instantaneous energy for δ= 20%, 15%, 10%, 5%

從圖9 中可以明顯地看出，對于不同的裂縫深度，瞬時頻率在裂紋位置處的峰值接近重疊，沒有明顯的區分度.輪載通過簡支梁全過程的瞬時能量曲線示于圖10.現取輪載未經過裂紋位置前的瞬時能量作為Ej，且Ej在 穩定范圍波動(t? ∈(0.25,0.5)) ；取輪載經過裂紋位置后的瞬時能量均值Ei， 且Ei在穩定范圍波動(t? ∈(0.65,0.9)) ，可求得均值能量差 ?E.圖11 給出了裂紋深度與 ?E的關系圖，可以清晰地看出，隨著裂紋深度的增加， ?E的值呈現出線性增加的趨勢.由此可知， ?E對損傷程度的大小有一定的敏感性.

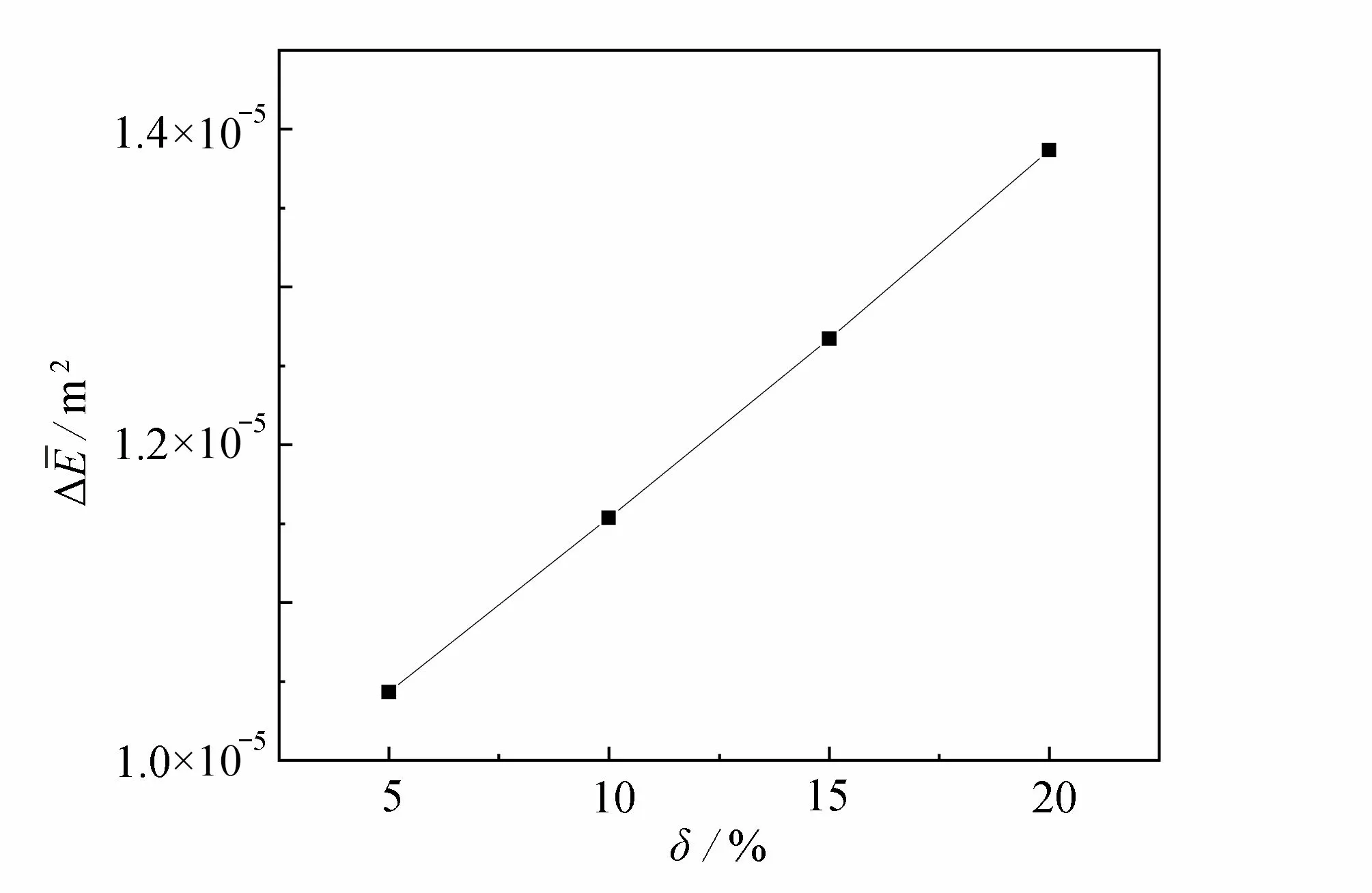
圖11 均值能量差Fig. 11 The mean energy difference

4.3 輪載大小影響分析

針對輪載大小對裂紋識別效果的影響，本文做了一定的分析.這里設置輪載大小分別為 5 kN，1 0 kN和15 kN三種情況，其他條件與工況1 相同，其瞬時能量示于圖12.從圖中可以看出，輪載大小的增加使得瞬時能量幅值也在不斷增加.圖13 給出了均值能量差 ?E與輪載大小的關系.為選取合適的Ei和Ej，采取與4.2 小節相同的做法.可以看出， ?E隨著輪載大小的增加而逐漸增加.這也說明 ?E可以區分不同輪載大小對檢測結果的影響.

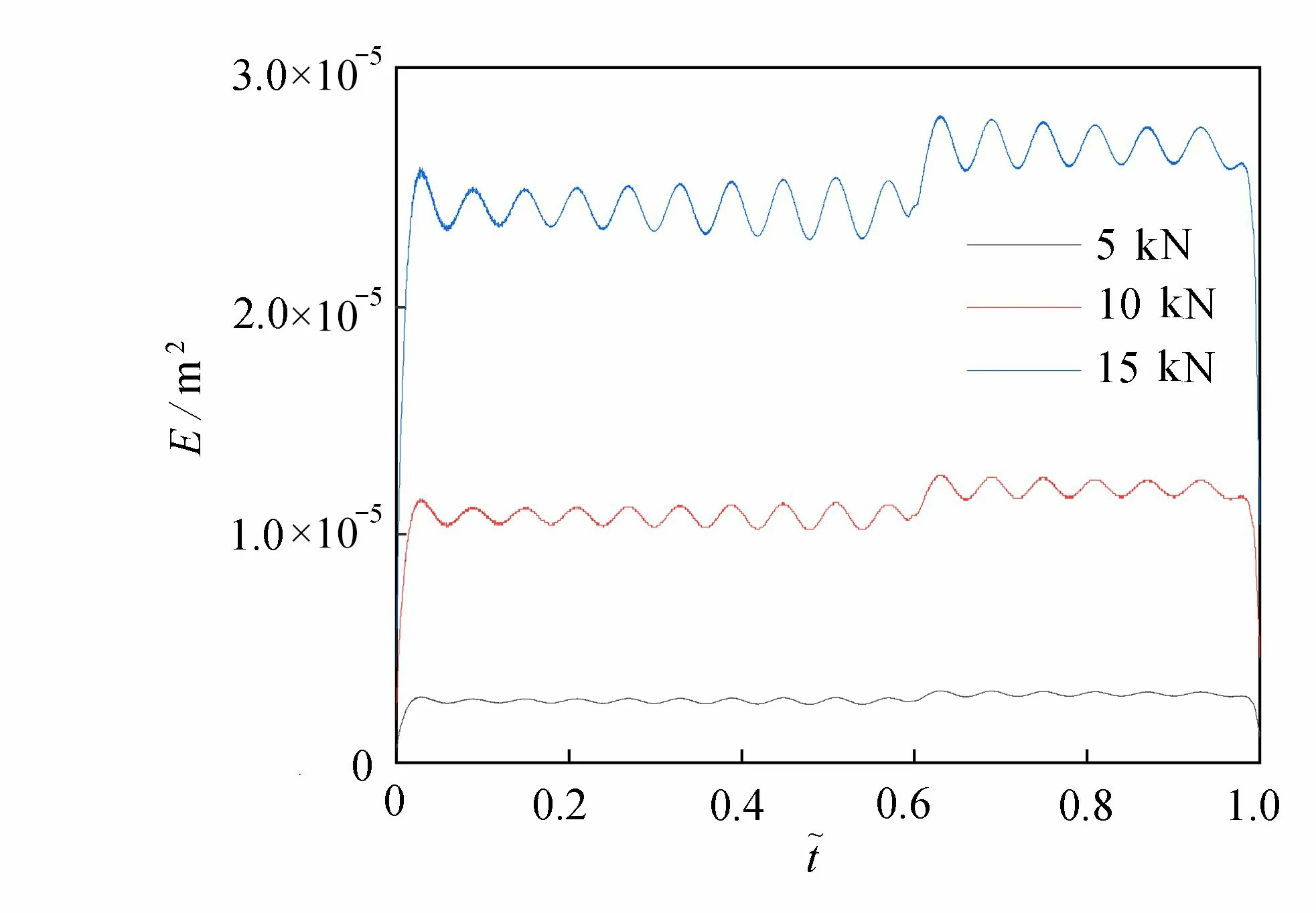
圖12 三種輪載大小作用下瞬時能量對比Fig. 12 Comparison of instantaneous energies under 3 wheel loads

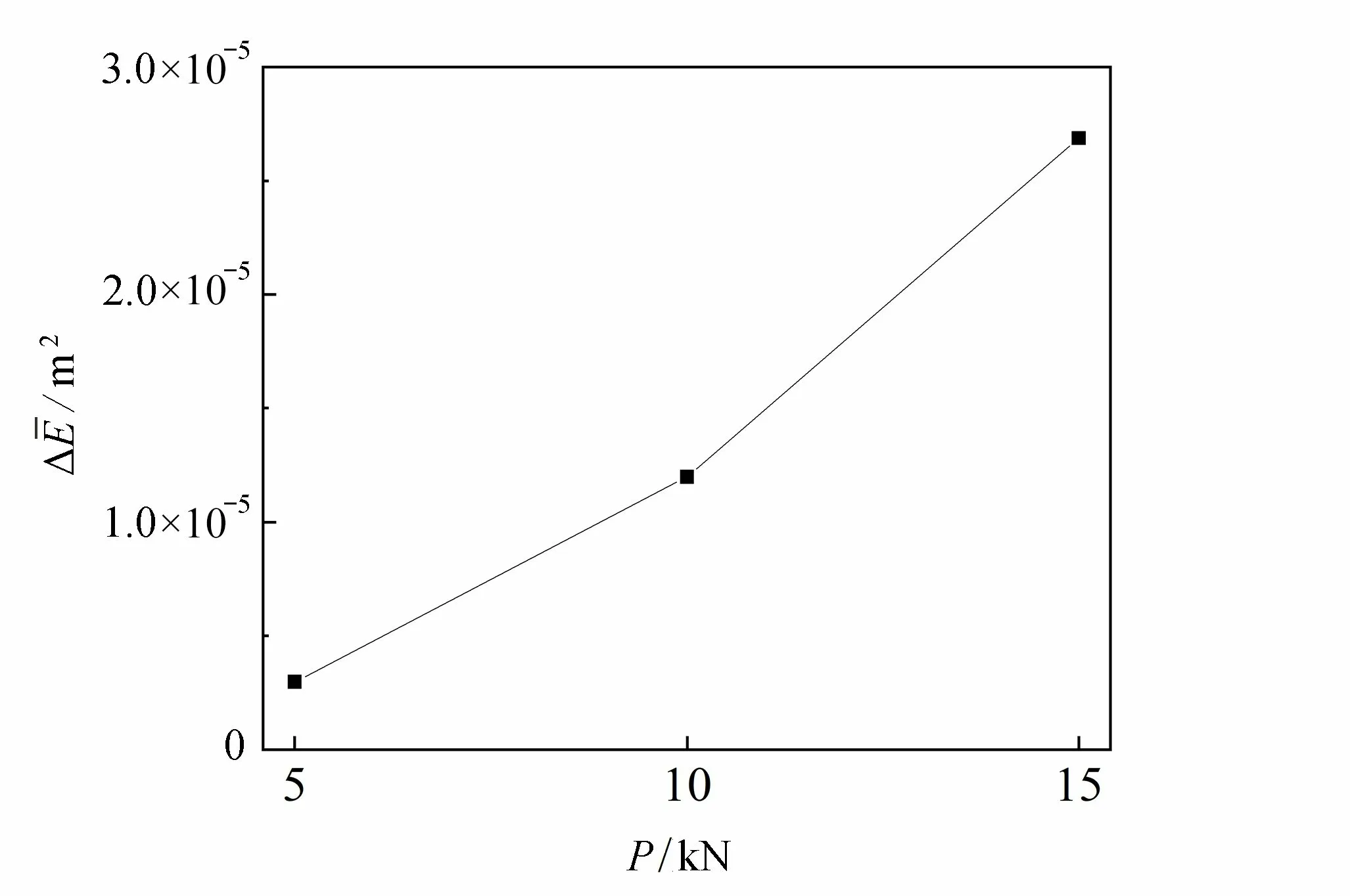
圖13 均值能量差（輪載大小）Fig. 13 The mean energy difference (wheel load size)

4.4 雙位置損傷分析

分別設置在6 m 和9 m 處存在裂紋損傷，并設置其裂縫高度占比 δ 分 別為 20%，1 5%，1 0%和 5%.在進行VMD 時，取α =9 000，其他參數不變.其瞬時頻率示于圖14.

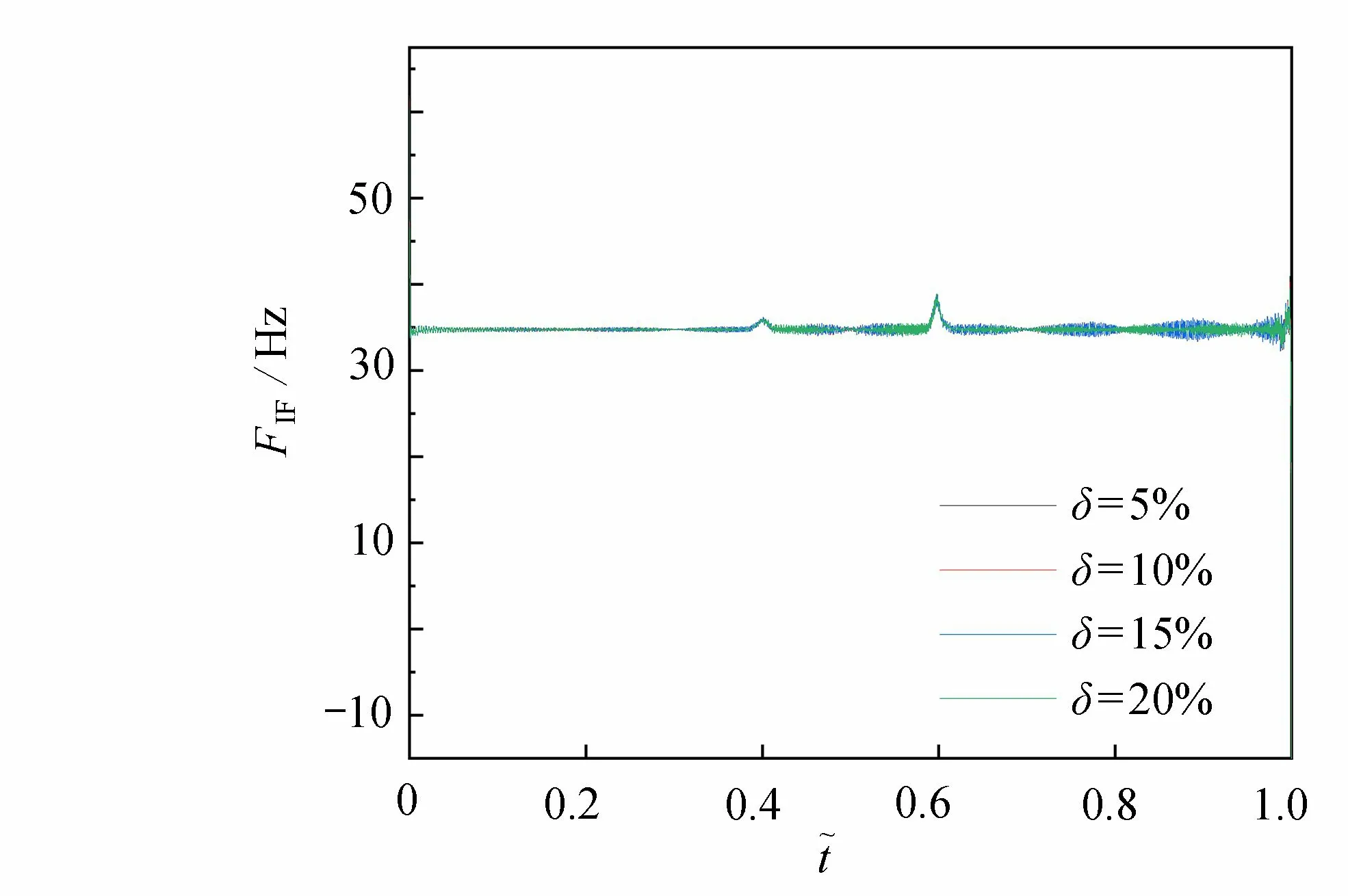
圖14 δ 為 20 % ，15% ，1 0% ，5% 的瞬時頻率對比（雙位置）Fig. 14 Comparison of instantaneous frequencies for δ= 20%, 15%, 10%, 5% (2 positions)

從圖14 可以看出，在6 m 和9 m 裂紋位置處，瞬時頻率幅值都有一定的峰值突出，且位于右側裂紋的瞬時頻率峰值更加尖銳.然而，對于不同裂紋深度的區分，瞬時頻率呈現的效果依然不佳.圖15 給出了兩處存在不同深度裂縫時的瞬時能量曲線.可以看出，瞬時能量波動范圍的均值在6 m 和9 m 位置處都有所提升.由圖16可知，在6 m 和9 m 位置處，隨著裂紋深度的增加 ?E的值大致呈現出線性遞增的趨勢.同時，Ei和Ej的選取與4.2 小節的做法基本相同.

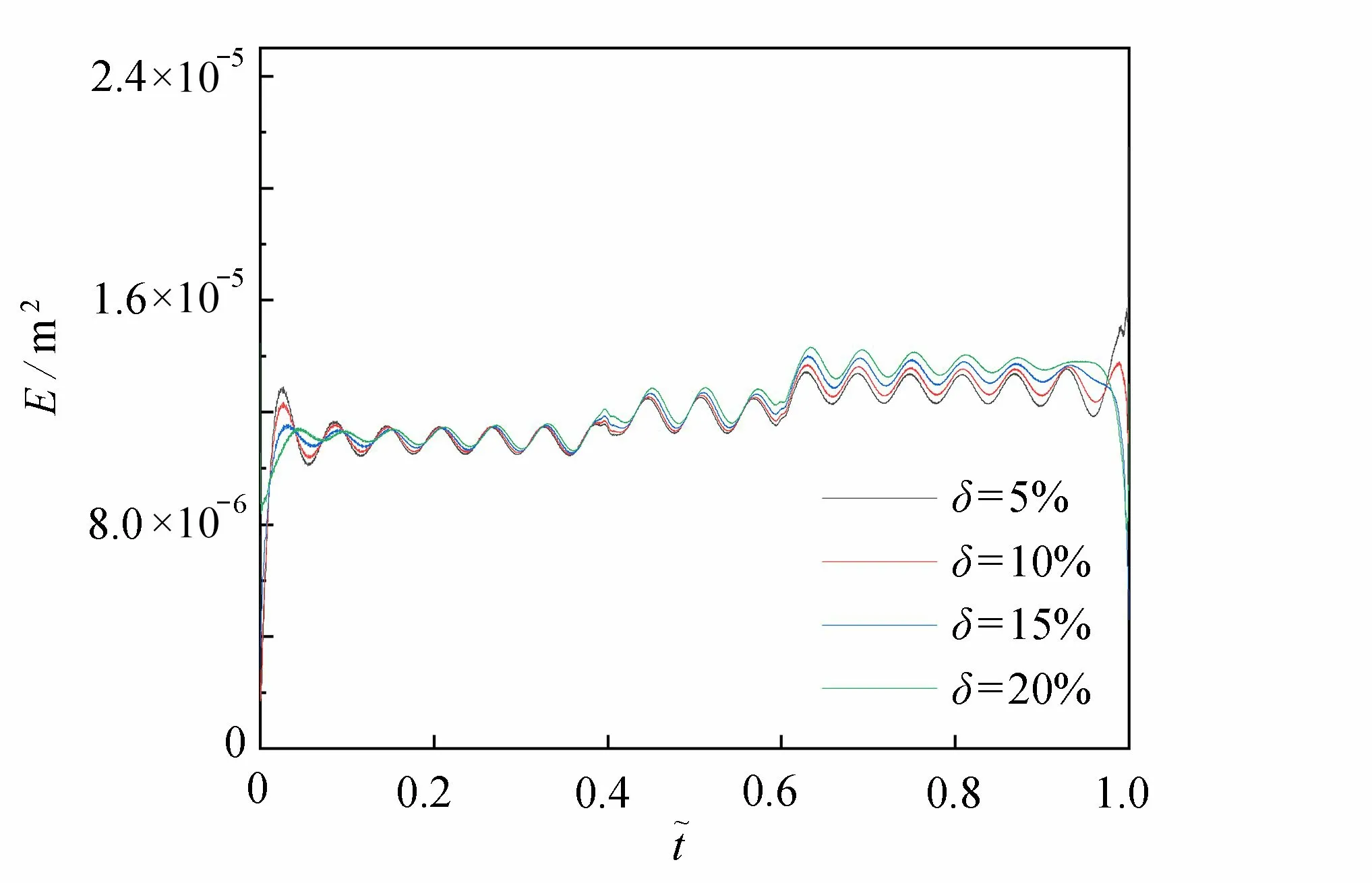
圖15 δ為2 0% ，15% ，1 0% ， 5% 的瞬時能量對比（雙位置）Fig. 15 Comparison of instantaneous energy for δ= 20%, 15%, 10%, 5% (2 positions)

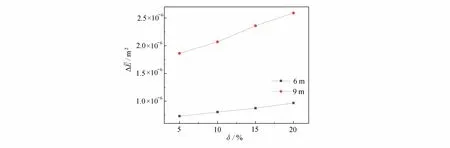
圖16 均值能量差（雙位置）Fig. 16 Mean energy differences (2 positions)

4.5 噪聲影響分析

在實際的橋梁損傷檢測中，環境噪聲往往對識別結果有一定的影響.擁有良好的噪聲魯棒性，也是評判檢測方法的重要因素.本文將三種不同程度的隨機噪聲添加到跨中加速度信號中，得到信噪比（SNR）分別為5 dB，1 0 dB和 1 5 dB的信號，其他條件與工況一相同.其瞬時頻率分別如圖17 ～ 19 所示.

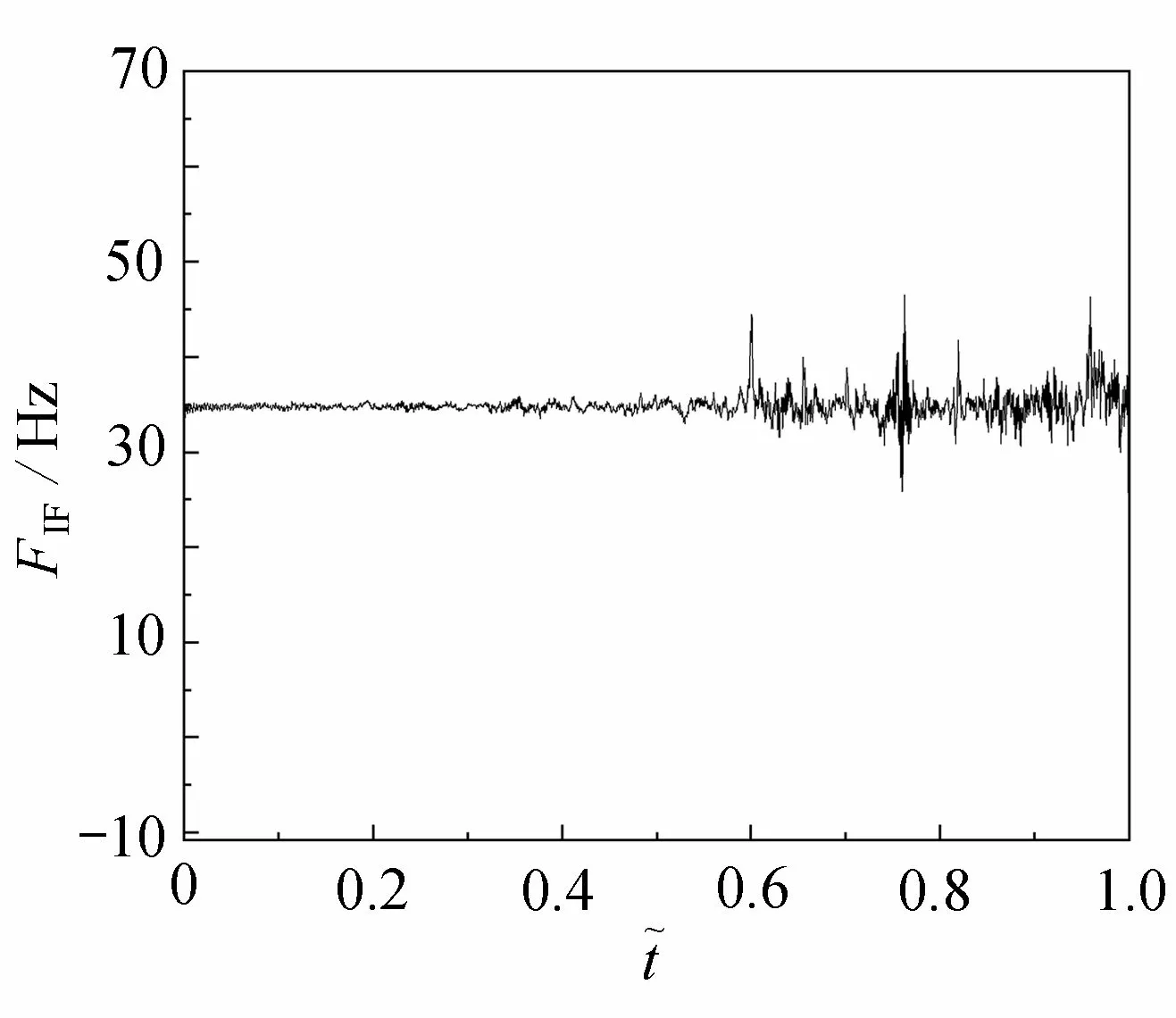
圖17 信噪比為5 dBFig. 17 The SNR is 5 dB

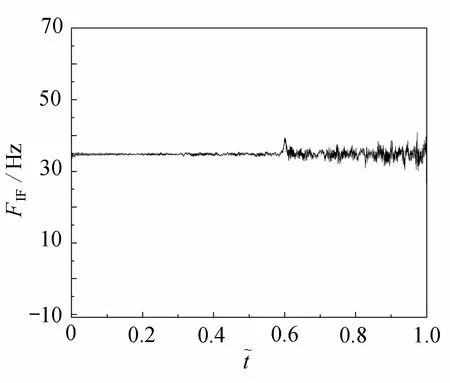
圖18 信噪比為10 dBFig. 18 The SNR is10 dB

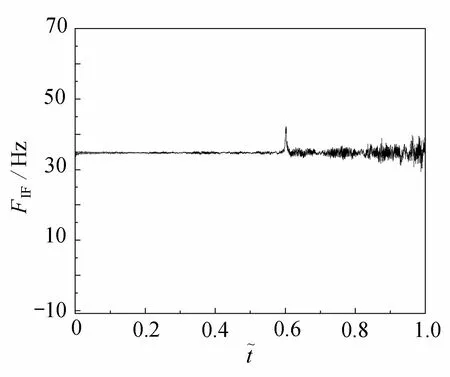
圖19 信噪比為15 dBFig. 19 The SNR is 15 dB

從圖中可以看出，當信噪比為5 dB時 ，9 m 處的裂紋位置很難識別；相較于信噪比5 dB， 在信噪比為1 0 dB的條件下，裂紋位置的識別效果較好，但是受到其他位置處瞬時頻率波動的干擾；當信噪比為1 5 dB時，裂紋位置的識別仍具有良好的效果.所以基于VMD 分解的損傷識別方法具有一定的噪聲魯棒性.

5 結 論

本文根據振動理論推導出了帶裂紋簡支梁在移動荷載作用下的動態響應表達式，發現在移動荷載經過裂紋位置后，其跨中加速度響應出現了幅值和相位的變化，為數值模擬提供了理論支持.此外，采用有限元軟件建立了符合規范的簡支梁橋，并采用車輪荷載作用在橋面，提取其跨中加速度響應進行裂紋識別.可得到如下結論：

1） 加速度響應經過VMD 分解后，IMF 4 和IMF 5 分別包含了相位和幅值的突變，可以利用瞬時頻率和瞬時能量進行體現；

2） 對于不同程度損傷的裂紋，甚至是深度占比為5%的小裂紋，瞬時頻率都能夠準確識別，但不能做到有效的區分，而均值能量差能夠很好區分不同的裂紋深度帶來的損傷；

3） 對雙位置裂紋的識別，瞬時頻率對裂紋位置的識別效果仍然可觀，同時也可以利用均值能量差區分不同的裂紋損傷程度；

4） 在1 5 dB 信噪比的條件下，瞬時頻率對裂紋位置的識別仍有良好的效果；

5） 該方法在不阻塞交通的前提下，僅需獲取損傷橋梁跨中加速度響應即可進行裂紋識別，對實際工程應用具有參考價值.

然而，由于本研究的對象僅為簡支梁橋這種常見橋型，對于其他類型的橋梁結構，該方法的實用性還需要進一步考證.

參考文獻（ References ） ：

［1］ZHU J, ZHANG Y. Damage detection in bridge structures under moving vehicle loads using delay vector variance method[J].Journal of Performance of Constructed Facilities, 2019, 33（5）: 4019049.

［2］ZHU X Q, LAW S S. Wavelet-based crack identification of bridge beam from operational deflection time history[J].International Journal of Solids and Structures, 2006, 43（7）: 2299-2317.

［3］ 劉光耀, 劉習軍, 張素俠, 等. 基于小波分析和變異系數的簡支梁橋損傷識別[J]. 應用力學學報, 2020, 37（5）: 1915-1922. （LIU Guangyao, LIU Xijun, ZHANG Suxia, et al. Damage identification of simply supported beam bridge based on wavelet analysis and variation coefficient[J].Chinese Journal of Applied Mechanics, 2020, 37（5）: 1915-1922.（in Chinese））

［4］KHORRAM A, BAKHTIARI-NEJAD F, REZAEIAN M. Comparison studies between two wavelet based crack detection methods of a beam subjected to a moving load[J].International Journal of Engineering Science, 2012,51: 204-215.

［5］ 劉小靖, 周又和, 王記增. 小波方法及其力學應用研究進展[J]. 應用數學和力學, 2022, 43（1）: 1-13. （LIU Xiaojing,ZHOU Youhe, WANG Jizeng. Research progresses of wavelet methods and their applications in mechanics[J].Applied Mathematics and Mechanics, 2022, 43（1）: 1-13.（in Chinese））

［6］HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London A:Mathematical,Physical and Engineering Sciences, 1998, 454（1971）: 903-995.

［7］MEREDITH J, GONZáLEZ A, HESTER D. Empirical mode decomposition of the acceleration response of a prismatic beam subject to a moving load to identify multiple damage locations[J].Shock and Vibration, 2012,19（5）: 845-856.

［8］ROVERI N, CARCATERRA A. Damage detection in structures under traveling loads by Hilbert-Huang transform[J].Mechanical Systems and Signal Processing, 2012, 28: 128-144.

［9］ 孟宗, 季艷, 谷偉明, 等. 基于支持向量機和窗函數的DEMD端點效應抑制方法[J]. 計量學報, 2016, 37（2）: 180-184.（MENG Zong, JI Yan, GU Weiming, at el. End effects restraining of DEMD based on support vector machine and window function[J].Acta Metrologica Sinica, 2016, 37（2）: 180-184.（in Chinese））

［10］ 邢昀, 榮劍. 常見不同模態信號分解方法探討[J]. 現代計算機, 2018, 36: 7-11. （XING Yun, RONG Jian. Discussion on the signal decomposition methods of common modes[J].Modern Computer, 2018, 36: 7-11.（in Chinese））

［11］DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J].IEEE Transactions on Signal Processing, 2014, 62（3）: 531-544.

［12］ 趙巖, 朱均超, 張寶峰, 等. 基于VMD與Hilbert譜的旋轉機械碰摩故障診斷方法[J]. 振動、測試與診斷, 2018, 38（2）:381-386. （ZHAO Yan, ZHU Junchao, ZHANG Baofeng, et al. Rub-impact fault diagnosis of rotating machinery based on VMD and Hilbert spectrum[J].Journal of Vibration,Measurement & Diagnosis, 2018, 38（2）: 381-386.（in Chinese））

［13］ 唐貴基, 王曉龍. 參數優化變分模態分解方法在滾動軸承早期故障診斷中的應用[J]. 西安交通大學學報, 2015,49（5）: 73-81. （TANG Guiji, WANG Xiaolong. Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing[J].Journal of Xi’an Jiaotong University, 2015, 49（5）:73-81.（in Chinese））

［14］ 趙昕海, 張術臣, 李志深, 等. 基于VMD的故障特征信號提取方法[J]. 振動、測試與診斷, 2018, 38（1）: 11-19.（ZHAO Xinhai, ZHANG Shuchen, LI Zhishen, et al. Application of new denoising method based on VMD in fault feature extraction[J].Journal of Vibration,Measurement & Diagnosis, 2018, 38（1）: 11-19.（in Chinese））

［15］BAGHERI A, ALIPOUR M, OZBULUT O E, et al. Identification of flexural rigidity in bridges with limited structural information[J].Journal of Structural Engineering, 2018, 144（8）: 4018126.

［16］ 王超, 毛羚. 基于VMD和廣義Morse小波的結構瞬時頻率識別[J]. 振動、測試與診斷, 2020, 40（5）: 957-962. （WANG Chao, MAO Ling. Instantaneous frequency identification of a structure using variational mode decomposition and generalized Morse wavelets[J].Journal of Vibration,Measurement & Diagnosis, 2020, 40（5） : 957-962.（ in Chinese））

［17］MOUSAVI M, HOLLOWAY D, OLIVIER J C, et al. Beam damage detection using synchronisation of peaks in instantaneous frequency and amplitude of vibration data[J].Measurement, 2021, 168: 1-14.

［18］CHONDROS T G, DIMAROGONAS A D, YAO J. A continuous cracked beam vibration theory[J].Journal of Sound and Vibration, 1998, 215（1）: 17-34.

［19］ 王揚. 復雜輪胎力作用下瀝青路面力學行為研究[D]. 博士學位論文. 北京: 北京交通大學, 2017. （WANG Yang.Study on mechanical behaviors of asphalt pavement under complicated tire force[D]. PhD Thesis. Beijing:Beijing Jiaotong University, 2017. （in Chinese））