死區輸入下未知嚴格反饋非線性系統自適應約束控制*

宮赤坤， 汝青楊， 袁立鵬

（1. 上海理工大學 機械工程學院，上海 200093；2. 哈爾濱工業大學 機電工程學院，哈爾濱 150001）

引 言

現實世界中存在著很多未知系統，這些未知系統給控制器的設計帶來了極大的困難.圍繞這類系統，國內外眾多學者研究出自適應[1-2]、神經網絡[3-4]、模糊控制[5-7]等理論，并應用到了此類系統中.同時，工業系統中也廣泛存在著非線性系統，非線性系統可劃分為嚴格反饋、純反饋、非嚴格反饋三種類型.其中，嚴格反饋系統是非常常見的系統，工業生產中存在許多嚴格反饋系統的模型，如液壓伺服系統[8]、導彈系統[9]等.

實際生產過程中，由于執行機構物理結構的限制，存在控制輸入的死區動態問題，如液壓執行器、機械連接和交流電機驅動等系統[10].死區特性是一種典型的非線性現象，許多學者對此展開了研究.如文獻[11]利用反步法與固定時間收斂解決了高階非線性系統死區輸入的控制問題，但反步法中存在微分爆炸問題.針對這一問題，文獻[12]提出指令濾波反步自適應控制，解決了這一問題.

對于非線性系統中的不確定性和復雜的外界干擾，通常利用擴張狀態觀測器(extended state observer,ESO)觀測其中無法直接獲得的內部動態[13].ESO 是自抗擾控制技術(active disturbance rejection control,ADRC)中最關鍵的部分[14].目前，對于ESO 技術涌現出大量的研究成果.如文獻[15]利用ESO 對伺服電動缸在外界干擾下進行補償控制.文獻[16]利用ESO 與有限時間控制方法相結合，使得嚴格反饋非線性系統跟蹤誤差收斂到平衡點的小區域內.上述研究成果因其使用的觀測函數都是非光滑的，可能出現高頻抖振的問題.文獻[17]對ESO 中的非線性函數進行改進，保證了原點處不會發生過沖的現象，但其控制參數增多，造成了控制器設計的復雜性.

預設性能約束控制近些年已成為控制理論研究的熱點問題，這種控制方法可以避免過大的超調對系統的損害，而且可以約束系統的收斂速度.具有預設約束的跟蹤控制是采用規定的性能函數將原系統的跟蹤誤差轉化為新的誤差系統，并結合到控制器的設計中[18].現有的文獻主要有兩類方法，即漏斗控制和預設性能控制.漏斗控制是高增益的時變控制方法.目前為止，這種方法已被應用到了許多實際問題中.如文獻[19]利用改進的漏斗函數與自適應神經網絡對存在擾動的伺服機構進行補償.文獻[20]設計了漏斗快速非奇異終端滑模面控制器，解決了機械臂在外部干擾下的高精度跟蹤控制問題.

基于以上討論，針對文獻[8-9]中需要對虛擬控制律的偏導數解析計算，文獻[15-16]使用ESO 過程中出現的抖振問題，同時沒有考慮到實際系統輸出誤差可能需要約束在一定范圍內，文獻[19-20]沒有考慮到實際系統中可能存在死區輸入造成控制系統性能惡化的問題，本文提出了基于免疫函數的自抗擾預設漏斗約束自適應控制策略.本文主要貢獻如下：針對傳統ESO 觀測過程中出現的抖振問題，引入光滑的免疫函數設計觀測器，從設計原理上消除了觀測過程中出現的抖振現象；解決了實際系統中可能存在死區輸入的問題，同時利用漏斗控制技術將輸出誤差約束在預設的范圍內；使用雙曲正切函數變化速率快這一特性設計了自適應控制律；控制器設計過程中使用指令濾波器，解決了反步法中微分爆炸的問題.

1 預備知識及問題描述

1.1 系統描述

考慮死區高階嚴格反饋非線性系統的跟蹤控制問題，這里給出其系統的一般模型如下：

1.2 免疫函數

免疫函數定義如下[23]：

1.3 漏斗約束函數

漏斗控制不僅將誤差維持在約束的范圍內，同時也消除了超調這一現象.漏斗約束表達式如下：

其中N(·)是 時變增益，p(t)是 尺寸曲線，l(t)是 約束曲線，//e(t)//是 變量e(t)的歐式范數.本文中選用的漏斗函數[24]如下所示：

其中 β0， β∞和c為 正常數，滿足條件 β0≥β∞>0.通過使用漏斗約束的控制方法，系統的輸出誤差可被約束在呈指數衰減的曲線范圍內.

2 漏斗約束控制器的設計

選取Lyapunov 函數：

3 穩定性分析

我們在前文給出控制器設計的基礎上，對整個系統的收斂性進行整體分析.

選取系統的Lyapunov 函數如下：

由式(40)可得閉環系統所有信號是最終有界的.

4 仿 真 算 例

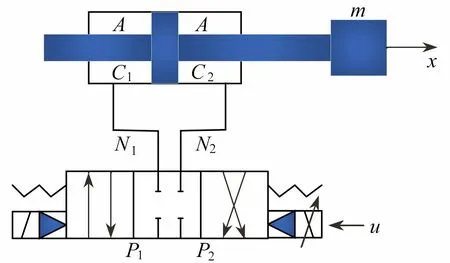
圖1 閥控液壓缸系統Fig. 1 The schematic diagram of the hydraulic servo system

選取狀態變量x=[x1,x2,x3]T=[x,x˙,F/m]T，可得其狀態方程模型為如下形式：

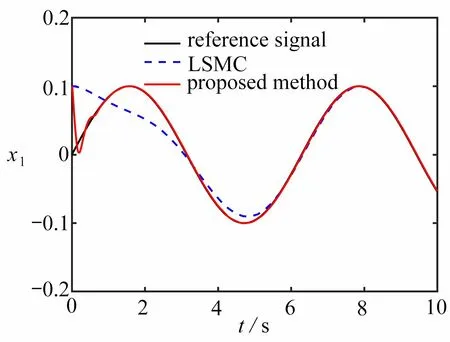
圖2 跟蹤曲線圖Fig. 2 The tracking curve

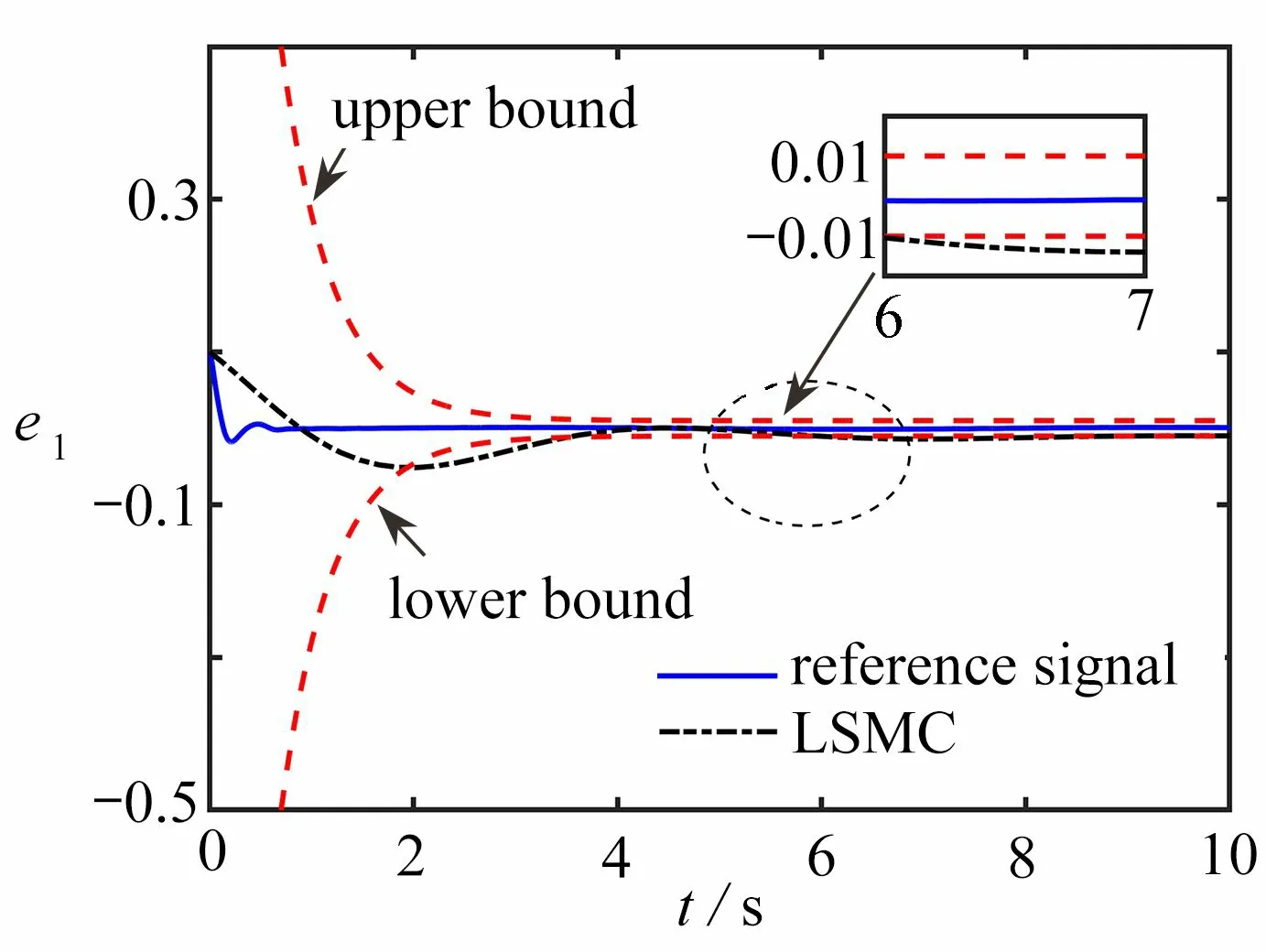
圖3 輸出誤差曲線圖Fig. 3 The error curve

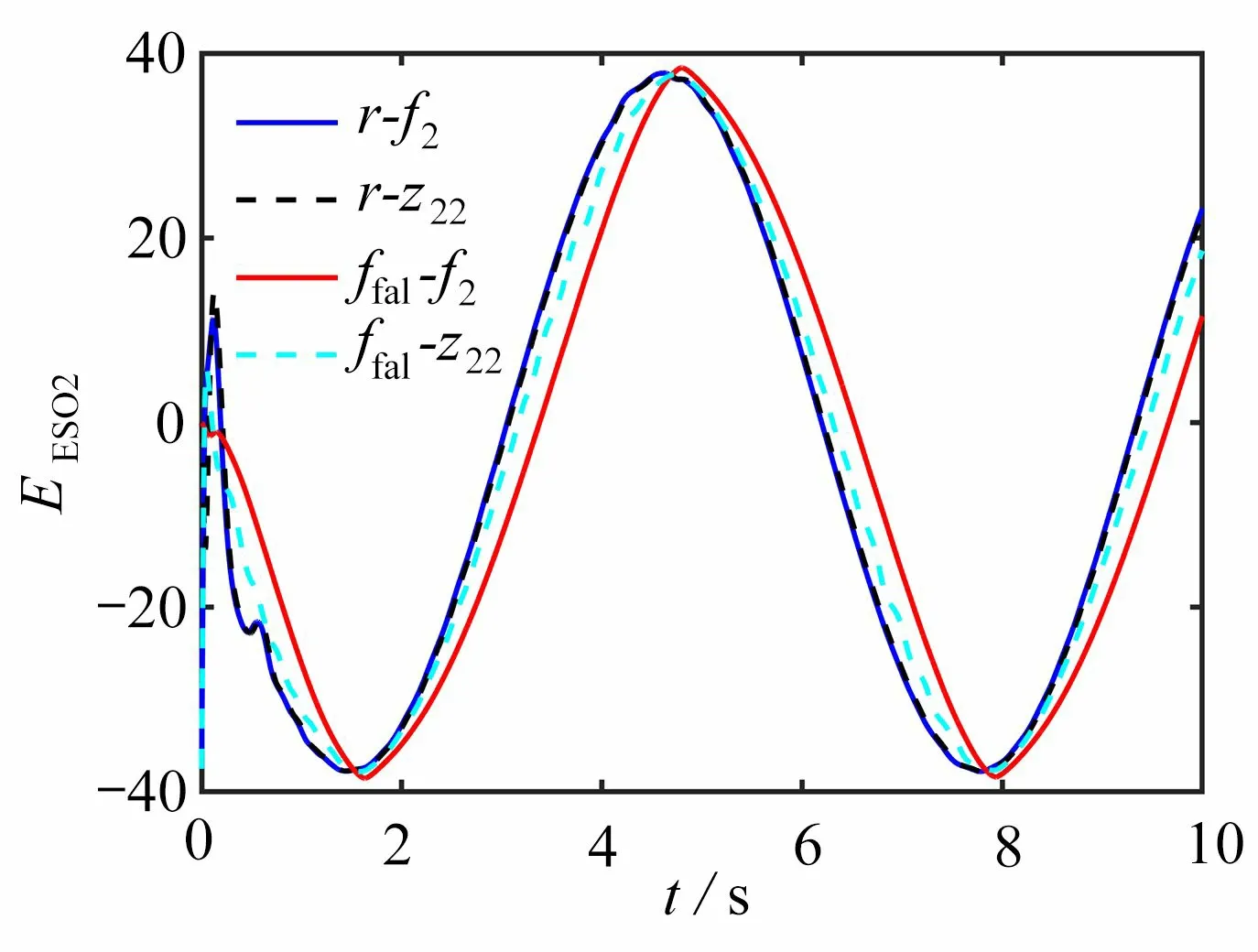
圖4 f2 和z 22的曲線Fig. 4 Curves of f2 and z22

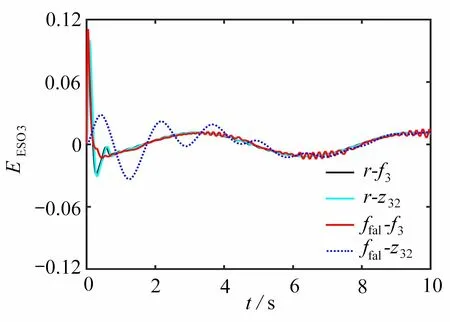
圖5 f3和 z 32的曲線Fig. 5 Curves of f3 andz32

圖2、3 表明，在系統(41)輸出存在初始誤差時，線性滑膜控制方法以及本文使用的免疫函數設計的控制器都能達到跟蹤的效果.但通過比較可以看出，本文所設計的控制器能夠在1 s 內實現系統輸出穩定跟蹤預設信號，并且最終輸出跟蹤誤差可以收斂在設定的小區間( ?0.01,0.01)內.從表1 中可以看出，本文控制方法誤差波動區間范圍更小，可以獲得更小的穩態誤差.圖4、5 展示出基于免疫函數的觀測器與基于ffal函數的觀測器各自的觀測效果.從圖4、5 可以看出，基于免疫函數的觀測器收斂速度更快，觀測效果更好，并且基于免疫函數的觀測器在瞬態階段出現超調是由于此觀測器瞬態收斂所導致，可以通過調節參數進行改進.

表1 兩種不同控制器的誤差分析Table 1 Error analysis for the control effects of 2 different controllers

為進一步體現本文所設計控制器的抗干擾性，在本文設計的輸入信號中加入擾動0 .2randn(1,1)，從而對本文控制系統的抗擾性能進行仿真研究，仿真結果如圖6、7 所示.圖6、7 中加入噪聲作為擾動信號的控制效果與圖2、3 中不加入噪聲的控制效果基本上是相同的，表明本文的控制器設計具有良好的抗外界干擾的能力，具有較強的魯棒性.

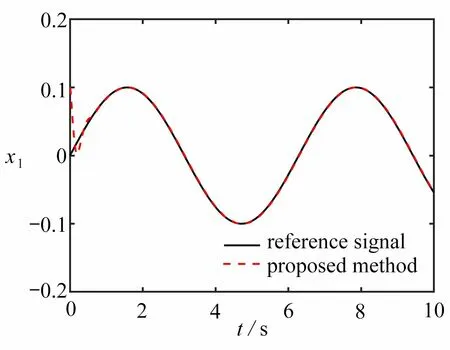
圖6 加入噪聲擾動跟蹤曲線圖Fig. 6 The tracking curve with noise

5 結 論

本文研究了一類具有死區輸入的預設約束未知高階嚴格反饋非線性系統的控制問題，利用光滑免疫函數設計觀測器，解決了系統中未知項無法直接獲取的問題，同時解決了觀測過程中的抖振問題.通過將漏斗控制技術、雙曲正切函數和自適應控制相結合，提出了一種新穎的自適應狀態反饋控制策略；引入指令濾波器處理反步法中微分爆炸問題.本文所提出的控制策略可以有效地跟蹤期望軌跡，而且誤差維持在預設的漏斗約束內，最后將本文的控制方法應用到液壓伺服驅動系統中，通過仿真結果證明了所設計控制器的有效性.但本文設計的控制器理論上達到最終的控制效果沒有時間約束要求，可進一步改進控制器使得其在固定時間內達到控制要求.

參考文獻（ References ） ：

［1］SHE X, LIU J, ALCAIDE A M, et al.Adaptive second-order sliding mode control for grid-connected NPC converters with enhanced disturbance rejection[J].IEEE Transactions on Power Electronics, 2022, 37（1）: 206-220.

［2］ZHOU Q, DU P, LI H, et al. Adaptive fixed-time control of error-constrained pure-feedback interconnected nonlinear systems[J].IEEE Transactions on Systems Man Cybernetics-Systems, 2021, 51（10）: 6369-6380.

［3］ 劉祥, 童東兵, 陳巧玉. 基于觀測器的非嚴格反饋時滯非線性系統的神經網絡自適應控制[J]. 應用數學和力學, 2021,42（6）: 586-594. （LIU Xiang, TONG Dongbing, CHEN Qiaoyu. Observer-based adaptive neural network control for nonstrict-feedback nonlinear systems with time delays[J].Applied Mathematics and Mechanics, 2021, 42（6）:586-594.（in Chinese））

［4］WANG T, GAO H, QIU J. A combined adaptive neural network and nonlinear model predictive control for multirate networked industrial process control[J].IEEE Transactions on Neural Networks and Learning Systems,2016, 27（2）: 416-425.

［5］TRUONG N, PHAM D H, VAN ANH H, et al. Fuzzy-based distributed behavioral control with wall-following strategy for swarm navigation in arbitrary-shaped environments[J].IEEE Access, 2021, 9: 139176-139185.

［6］AYMEN F, MOHAMED N, CHAYMA S, et al. An improved direct torque control topology of a double stator machine using the fuzzy logic controller[J].IEEE Access, 2021, 9: 126400-126413.

［7］WANG Z, ZOU L, SU X, et al. Hybrid force/position control in workspace of robotic manipulator in uncertain environments based on adaptive fuzzy control[J].Robotics and Autonomous Systems,2021, 145: 103870.

［8］GUAN C, PAN S. Nonlinear adaptive robust control of single-rod electro-hydraulic actuator with unknown nonlinear parameters[J].IEEE Transactions on Control Systems Technology, 2008, 16（3）: 434-445.

［9］LI Z, ZHANG R. Time-varying sliding mode control of missile based on suboptimal method[J].Journal of Systems Engineering and Electronics, 2021, 32（3）: 700-710.

［10］YU J, SHI P, DONG W, et al. Adaptive fuzzy control of nonlinear systems with unknown dead zones based on command filtering[J].IEEE Transactions on Fuzzy Systems, 2018, 26（1）: 46-55.

［11］LI H, HUA C, LI K. Fixed-time stabilization for interconnected high-order nonlinear systems with dead-zone input and output constraint[J].Journal of the Franklin Institute, 2021, 358（14）: 6923-6940.

［12］DONG W, FARRELL J A, POLYCARPOU M M, et al. Command filtered adaptive backstepping[J].IEEE Transactions on Control Systems Technology, 2012, 20（3）: 566-580.

［13］XIA Y, ZHU Z, FU M. Back-stepping sliding mode control for missile systems based on an extended state observer[J].IET Control Theory and Applications, 2011, 5（1）: 93-102.

［14］TALOLE S E, KOLHE J P, PHADKE S B. Extended-state-observer-based control of flexible-joint system with experimental validation[J].IEEE Transactions on Industrial Electronics, 2010, 57（4）: 1411-1419.

［15］ 鄭懷航, 王軍政, 劉冬琛, 等. 融合前饋與姿態預測的并聯穩定平臺自抗擾控制策略[J]. 機械工程學報, 2021, 57（9）:19-27. （ZHENG Huaihang, WANG Junzheng, LIU Dongchen, et al. Active disturbance rejection control strategy of parallel stable platform based on feedforward and attitude prediction[J].Journal of Mechanical Engineering,2021, 57（9）: 19-27.（in Chinese））

［16］ 張立鵬, 李小華, 何志江. 嚴格反饋非線性系統基于事件觸發的自抗擾預設有限時間跟蹤控制[J]. 信息與控制, 2021,50（4）: 441-448, 458. （ZHENG Lipeng, LI Xiaohua, HE Zhijiang. Event-triggered preassigned finite-time tracking control with active disturbance rejection for a class of strict feedback nonlinear systems[J].Information and Control, 2021, 50（4）: 441-448, 458.（in Chinese））

［17］ 蒲明, 劉鵬, 熊皚. Fal函數的改進及3種新型非線性擴張狀態觀測器[J]. 控制與決策, 2021, 36（7）: 1655-1662. （PU Ming, LIU Peng, XIONG Ai. Advanced Fal function and three novel nonlinear extended state observers[J].Control and Decision, 2021, 36（7）: 1655-1662.（in Chinese））

［18］CHENG Y, REN X, ZHENG D, et al. Non-linear bandwidth extended-state-observer based non-smooth funnel control for motor-drive servo systems[J].IEEE Transactions on Industrial Electronics, 2022, 69（6）: 6215-6224.

［19］WANG S, YU H, YU J, et al. Adaptive neural funnel control for nonlinear two-inertia servo mechanisms with backlash[J].IEEE Access, 2019, 7: 33338-33345.

［20］WANG H, FANG L, HU M, et al. Adaptive funnel fast nonsingular terminal sliding mode control for robotic manipulators with dynamic uncertainties[J].Journal of Mechanical Engineering Science, 2021, 235（18）: 3678-3693.

［21］LI H, ZHAO S, HE W, et al. Adaptive finite-time tracking control of full state constrained nonlinear systems with dead-zone[J].Automatica, 2019, 100: 99-107.

［22］MA M, WANG T, GUO R, et al. Neural network-based tracking control of autonomous marine vehicles with unknown actuator dead-zone[J].International Journal of Robust and Nonlinear Control, 2022, 32（5）: 2969-2982.

［23］ 曾喆昭, 吳亮東, 陳韋名. 基于ESO的一類線性時變系統自學習滑模控制方法[J]. 控制與決策, 2016, 31（11）: 2101-2105. （ZENG Zhezhao, WU Liangdong, CHEN Weiming. Self-learning sliding mode control method of a class of linear time-varying systems based on ESO[J].Control and Decision, 2016, 31（11）: 2101-2105.（in Chinese））

［24］ZHANG J, YANG G. Prescribed performance fault-tolerant control of uncertain nonlinear systems with unknown control directions[J].IEEE Transactions on Automatic Control, 2017, 62（12）: 6529-6535.

［25］NA J, LI Y P, HUANG Y B, et al. Output feedback control of uncertain hydraulic servo systems[J].IEEE Transactions on Industrial Electronics, 2020, 67（1）: 490-500.