考慮因素交互作用的車—車事故嚴重程度分析

張道文 ，王朝健，蔣 駿，黎華惠

（1.西華大學 汽車與交通學院，成都 610039，中國；2.汽車測控與安全四川省重點實驗室，成都 610039，中國；3.四川省新能源汽車智能控制與仿真測試技術工程研究中心，成都 610039，中國；4.成都工業職業技術學院，成都 610218，中國）

2020 年，中國大陸機動車導致的交通事故數達21.1 萬起，造成5.6 萬人死亡、21.4 萬人受傷和12.28億元直接財產損失[1]。交通事故可以分為車與人事故、車與二輪車或三輪車事故以及單車事故（即本車事故）、車對車（V2V）事故（以下又稱雙車事故）、多車事故。V2V 事故嚴重程度不僅取決于己方駕駛員和車輛的特征，還取決于對方駕駛員和車輛的特征[2]，且V2V 事故的占比高于其他事故類型[3]。因此研究雙車事故嚴重程度的關鍵因素，以及因素的交互作用對致死事故率的影響，對預防V2V 事故和降低駕乘人員的傷亡具有重要意義。

對V2V 事故的研究主要基于Logit 模型（Logit model）、Probit 模型（Probit model）等線性模型而限制了邏輯相關變量的引入。C.Duncan 等[4]采用有序Probit 模型（ordered Probit model），研究了V2V 事故中乘用車駕駛員損傷嚴重程度的影響因素。G.A.Torr?o 等[5]采用Logit 模型發現了V2V 事故中，對方汽車的發動機排量是重要影響因素。賈雄文[3]利用二項有序Probit 模型（bivariate ordered Probit，BOP），研究了國內V2V 事故受傷嚴重程度的關鍵影響因素。隨后賈雄文等[6]利用BOP 模型，研究了道路環境因素對V2V 事故嚴重程度的影響，發現道路等級的提升會降低駕駛員的受傷程度。蔣欣國等[7]利用廣義有序Logit模型（generalized ordered Logit），研究了雙方駕駛員的危險行為對V2V 事故的影響，發現超速和其他行為同時存在時對事故后果有顯著影響。王健宇等[8]基于多項Logistic 回歸模型（multinomial Logistic regression，MNL），研究了V2V 事故嚴重程度的影響因素及機理，探索了在不同嚴重程度的交通事故中影響因素存在的差異性。一些學者研究V2V 事故時，駕駛員因素一般僅考慮了受傷更嚴重的一方駕駛員；主要基于單因素分析，沒有考慮因素的交互作用，而交通事故是多風險因素對事故傷亡的綜合效應。

針對因素交互作用對事故嚴重程度的研究，有學者利用Shapley 加和解釋（Shapley additive explanations，SHAP）結合XGBoost[9]、LightGBM[10]等模型，但這種方法只能分析2 個因素的交互效應對事故后果的影響趨勢，不能量化分析[9]。有學者提出利用N-K 模型量化多種因素的交互作用對事故后果的影響[11]，但N-K模型只能解決因素之間的整體交互效應，不能分析因素具體狀態值的交互效應。有學者利用故障樹[12]、關聯規則[16]提取具有強耦合度的規則，但這些方法也不能具體量化規則對事故后果的影響程度。

Bayes 網絡（Bayesian networks,BN）模型具有高解釋度的優勢，已應用于交通安全的研究[14]。它能量化單因素以及多因素的交互作用對事故后果的影響，但多因素分析時，會面臨因素組合過多、主觀定義的組合耦合度低甚至為不可能事件等問題，而關聯規則剛好能彌補這一缺陷。

本文運用Bayes 網建立考慮風險因素交互作用的V2V 事故嚴重程度模型。定量分析關鍵影響因素、雙因素的交互作用對致死事故率的影響，結合關聯規則方法挖掘高頻率和強耦合度的規則，探究多因素交互作用下對致死事故率的影響，以期明確V2V 事故的預防重點，從而實施精準的防控策略。

1 方 法

1.1 Bayes 網絡

Bayes 網絡（BN）是一種描述變量間不確定因果關系的網絡模型，能很好地捕捉變量之間的潛在影響關系，有結構學習和參數學習2 個部分。當隨機變量有n個時，變量之間的關系可以由一個聯合概率分布表示：

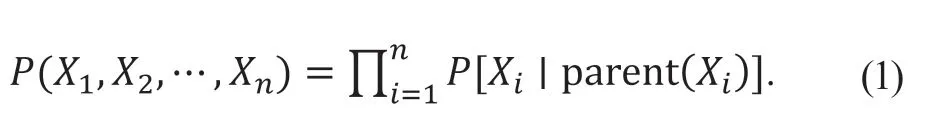
式中：X1、X2、…、Xn為隨機變量；parent(Xi)為隨機變 量Xi的全部父節點集合。當（parent(Xi)=? 時，parent[Xi｜parent(Xi)]是邊緣分布P(Xi)。

結構學習中，增強樸素Bayes（augmented naive Bayes，ANB）算法克服了傳統樸素Bayes 算法中因素局部獨立性的限制、應用廣泛[15]。完整數據的參數學習通常利用最大似然估計，定義如下：

P(｜θ=θ0)表示參數θ的某個取值θ0與數據的擬合程度，取值越大說明θ0與數據的擬合程度越高。給定θ，數據的條件概率P(｜θ)稱為θ的似然度：

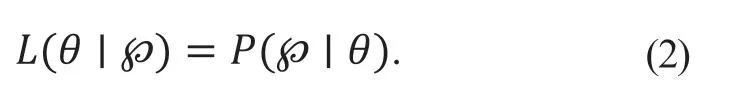
令L(｜θ)達到最大值時的取值θ*為參數θ的最大似然估計（maximum likelihood estimation，MLE)：

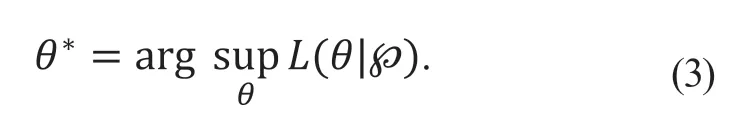
1.2 關聯規則

關聯規則算法可以挖掘要素之間的內在聯系，用X≥Y表示，X為前項，Y為后項。一般有支持度和置信度2 個衡量指標。

支持度指X和Y的同時出現的概率，用support（X≥Y）表示，置信度指出現后，出現的概率，用confidence（X≥Y）=P(Y｜X)表示。支持度越高表示前項出現的概率越高，置信度越高代表前項發生，后項出現的概率越高[16]。

1.3 驗證

常用的驗證方法有K折交叉驗證、接受者操作特性曲線（receiver operator characteristic，ROC 曲線）和ROC 曲線下的面積（area under curve，AUC）。K折交叉驗證將數據集劃分為K個大小相等的部分，K-1 部分用于訓練，最后K個部分用于測試，這個過程重復K次[15]。留一法（leave one out,LOO）是K折交叉驗證的極端情況，它將數據集的n-1 條數據用于訓練，最后一條數據用于測試，這個過程重復n次，驗證過程沒有隨機因素的影響，結果穩定[17]。

2 數據處理及模型建立

2.1 數據處理

(中國)國家車輛事故深度調查體系（national automobile accident in-depth investigation system，NAIS）由(中國)國家市場監督管理總局缺陷產品管理中心聯合中國8 所高校、多家交通司法鑒定中心共同建立[18]。事故數據覆蓋了中國大陸7 個地域，已有學者利用該數據庫進行了相關研究并取得了成果[19-21]。

對樣本進行以下初步篩選：

1）剔除由于研究對象為V2V 事故，需涉及行人、機動二三輪車、非機動二三輪車、V2V 和多車的事故；

2）剔除與研究無關的字段，同時剔除剩余字段中不完整的數據；

3）由于高速公路為封閉式道路管理，有別與其他道路，因此剔除涉及高速公路的案例[22]；

4）刪除剩余事故中的特殊案例，例如靜止車輛由于制動失效導致的事故、車輛自燃導致的事故。最終剩下583 例事故。

2.2 變量選取

交通事故的影響因素眾多，總體可分為人、車、路和環境4 個方面。人的方面主要包括駕駛人的心理因素和生理因素，例如駕駛人的年齡、性別和狀態等因素會影響駕駛員的感知能力和反應能力；車是人的載體，車輛的類型和安全技術狀況會間接影響事故后果，而駕駛人對車輛的控制會直接影響車輛的運動狀態；道路是交通的載體，主要包括發生地點、行政等級和路面狀況等因素；環境通過影響人、車和路方面而間接影響事故的發生，一般指自然環境的因素，例如天氣狀況、事故發生的時段。

考慮以往研究的變量選取并結合NAIS 數據庫的字段特征，從人、車、路和環境4 個方面選取17 個變量（包括影響因素和事故嚴重程度）[3,6,11,27]，分為過失方因素（L1-L5）、受害方因素（I1-I5）、道路因素（R1-R4）、環境因素（E1-E2）和事故嚴重程度（Sev），各變量取值及離散情況見表1。

表1 變量取值及離散情況

2.3 結構建立

運用GeNIe3.0 軟件進行結構學習和參數學習，得到V2V 事故嚴重程度分析模型的Bayes 網絡結構圖，一共包括17 個節點和29 條邊，如圖1 所示。其中：每一個節點代表一個變量，節點之間的連線代表變量之間具有直接依賴關系，如天氣狀況（E1）與路面狀況（R2）有直接依賴關系。

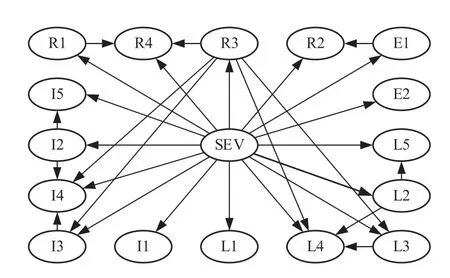
圖1 Bayes 網絡結構圖

2.4 模型驗證

利用留一法進行模型驗證，模型的準確率為81.3%，若準確率達80%，代表預測效果較好[24]。ROC 曲線下的面積（AUC）為0.81，表明算法的魯棒性較好，因此V2V 事故嚴重程度分析模型較合理。接受者操作特性曲線（ROC 曲線）和AUC 如圖2 所示。

圖2 ROC 曲線和AUC

3 推理分析

3.1 關鍵因素分析

為探究事故嚴重程度的關鍵影響因素，基于Bayes網絡構建的分析模型，輸入每個變量的各個取值狀態（對于每一個變量，其中一個取值的概率被設置為100%，同一變量的其他取值被設置為0%，例如過失方性別為男性，則女性的概率為0%），然后更新整個模型，觀察該變量的不同取值下致死事故率的變化。其中每個變量的不同取值狀態對致死事故率的最大影響幅度見表2。

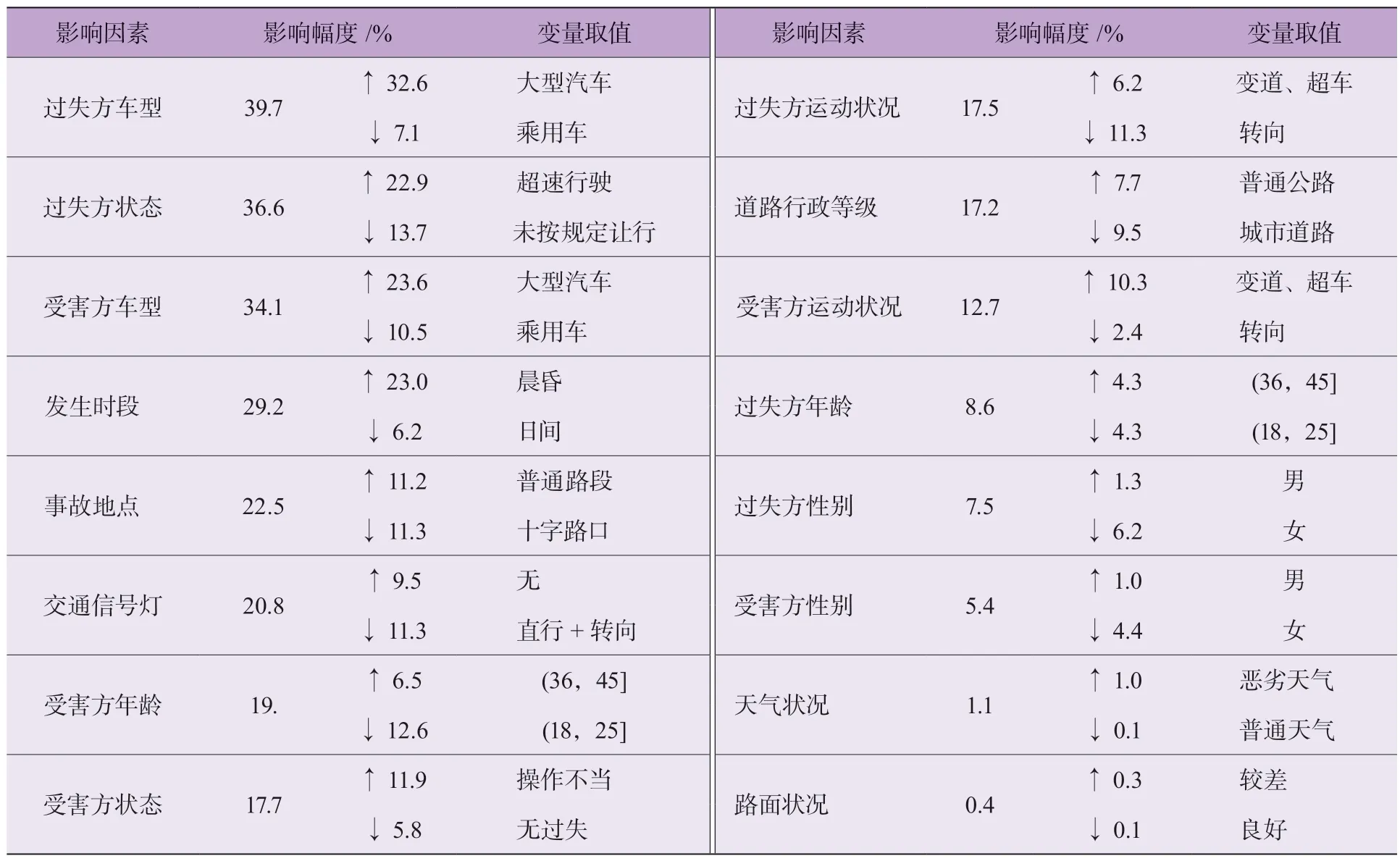
表2 各因素對致死事故率的影響幅度

“↑”代表取值對致死事故率的最大增幅；“↓”代表取值對致死事故率的最大降幅。例如過失方車型（因素L5）對致死事故率的影響幅度為39.7%，其中大型汽車因素會提高32.6%致死事故率（后文涉及的提高與降低均是相較于致死事故率的先驗概率），乘用車因素會降低7.1%致死事故率。

由表2 可知，L5、L3、I5、E2、R3、R4 等因素對致死事故率的影響幅度均超過20%，是引發致死事故的關鍵因素。過失方或受害方為大型汽車、過失方超速行駛會顯著提高致死事故率[7]；調整模型發現夜間（4.5%）的致死事故率高于日間[25]。發生在晨昏的事故占比僅6%，但該時段一旦發生事故，致死事故率會提高23%，相反發生在日間的事故占比最高，但致死事故率會降低6.2%。可能是晨昏車流量小，駕駛員警惕較低，導致行駛速度較快，而日間車流量大且行車視距較好，駕駛員更加謹慎[3]；普通路段和十字路口的事故占比較高，但十字路口比普通路段的致死事故率低22.5%[23]；設立信號燈能降低致死事故率，設立直行+轉向交通信號燈路段比無交通信號燈路段的致死事故率低20.8%，這是因為交通信號燈對駕駛員有警示作用，能降低交通沖突程度[23]。

(36，45]歲的駕駛員會略微提高致死事故率，而(18，25]歲的駕駛員會降低致死事故率。Lee C[25]指出30 歲以下的年輕司機在碰撞中受傷程度會降低，并且(18，25]歲的青年駕駛員由于駕駛經驗不豐富，警惕性反而更高；過失方或受害方的轉向行為均會降低致死事故率，但過失方的轉向行為降低幅度更大，可能是因為過失方處于轉向時，能更好的提前發現碰撞目標，實施主動避險行為；普通公路比城市路段的致死事故率高17.2%。男性駕駛員、惡劣天氣和較差的路面狀況等因素都會提升致死事故率，但影響程度較小。

3.2 二維推理分析

為考察雙因素的聯合效應對致死事故率的影響，以致死事故率的影響幅度中最大的因素L5 與其余關鍵因素進行組合分析，觀察2 個變量的不同取值組合的致死事故率，各組合的聯合效應見圖3。其中縱坐標底部為過失方車型的變量取值，縱坐標中部為其余關鍵因素的變量取值，橫坐標為該組合的致死事故率。

由圖3 可知：因素交互作用下，因素的聯合效應顯著。例如相較于過失方為乘用車，過失方為大型汽車與其余關鍵因素的交互作用更容易引發致死事故，尤其是駕駛員處于超速行駛或處于晨昏時段，因此建議大型汽車強制裝配超速報警裝置，并且駕駛員在晨昏等光線不好的環境要提高駕駛警惕；因素的聯合效應影響高于各自邊際效應之和。例如過失方為大型汽車且發生于普通路段時，致死事故率提高的邊際效應之和為42.1%，而聯合效應之和為44.4%。

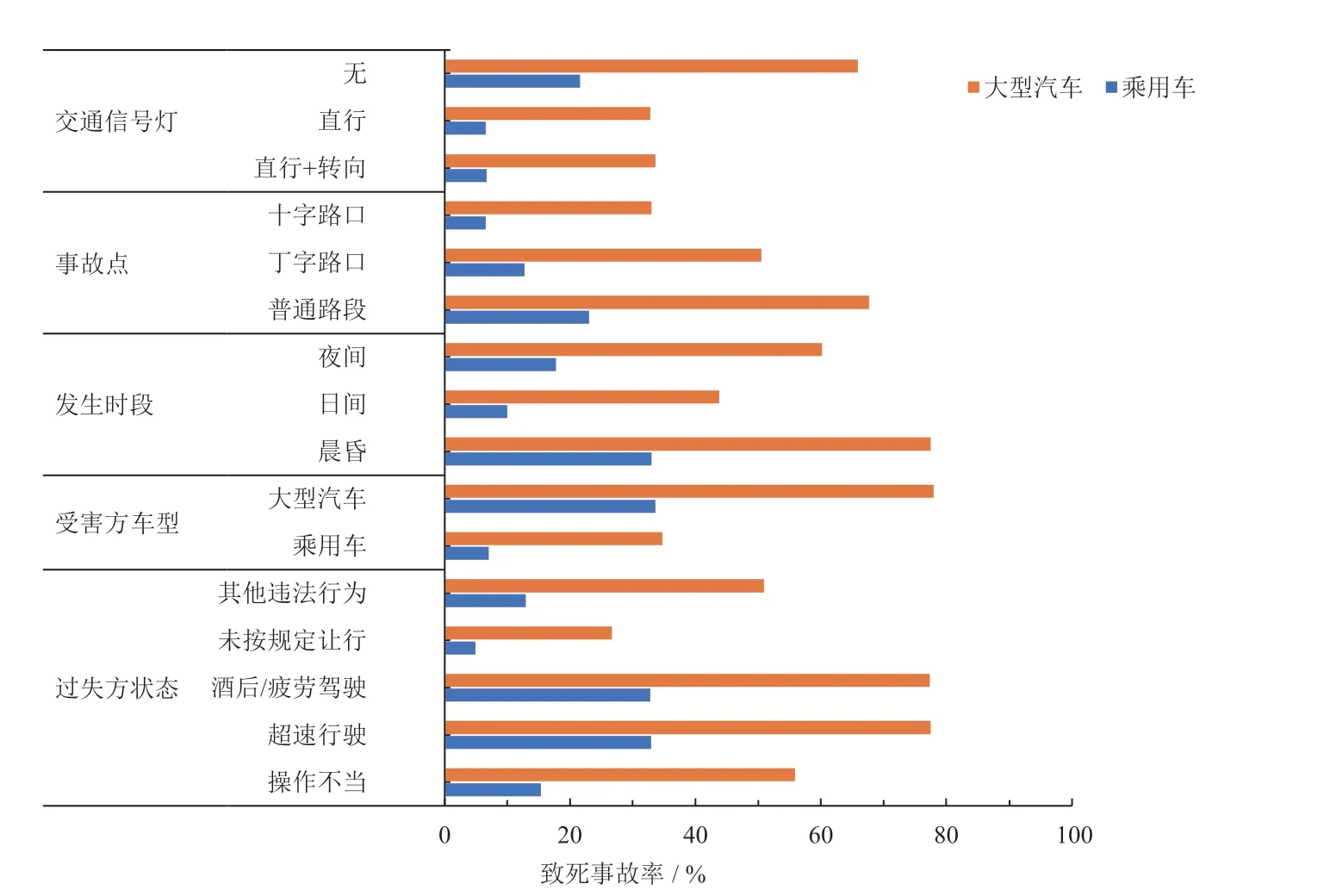
圖3 過失方車型和其余關鍵因素的聯合效應

3.3 多維推理分析

交通事故是多風險因素對事故傷亡的綜合效應，但面臨因素取值的組合過多、主觀定義的組合耦合度低甚至為不可能事件等問題。因此利用SPSS Modeler軟件的關聯規則挖掘關鍵因素中高頻率與強耦合度的規則，將關聯規則輸出的規則中各個變量的取值，作為Bayes 網絡分析模型中每個變量的輸入，計算各個規則的致死事故率的變化。為了挖掘高頻率和強耦合度的規則，設定最低支持度為20%和最低置信度為80%，剔除前后項內容相同的規則后，最終得到10 條規則見表3。

表3 可知：規則1 的支持度最高，說明該組合出現的頻率較高，但此時致死事故率會下降18.3%。這和C.Lee[25]結論類似，小型車之間的碰撞增加了非致死事故率，并且車輛在通過交叉口時的車速較低，因此降低了致死事故率[26]；規則2 出現的頻率較高，會小幅度提升致死事故率；與規則2 類似的是規則5，但規則5 發生時會增加42.6%的致死事故率，這是由于受害方為大型汽車時，盡管會降低受害方駕駛員的致死率，但會顯著提高過失方駕駛員的致死率[23]；規則7是唯一含夜間的高耦合規則，這種事故容易發生在無交通信號燈的普通路段，并會提高21.7%的致死事故率。這極大可能是因為夜間車流量低、無交通信號燈的警示，并且普通路段的干擾小，此時汽車的行駛速度較快，加上夜間視野差，導致發生緊急情況時駕駛員的避撞時間不足。

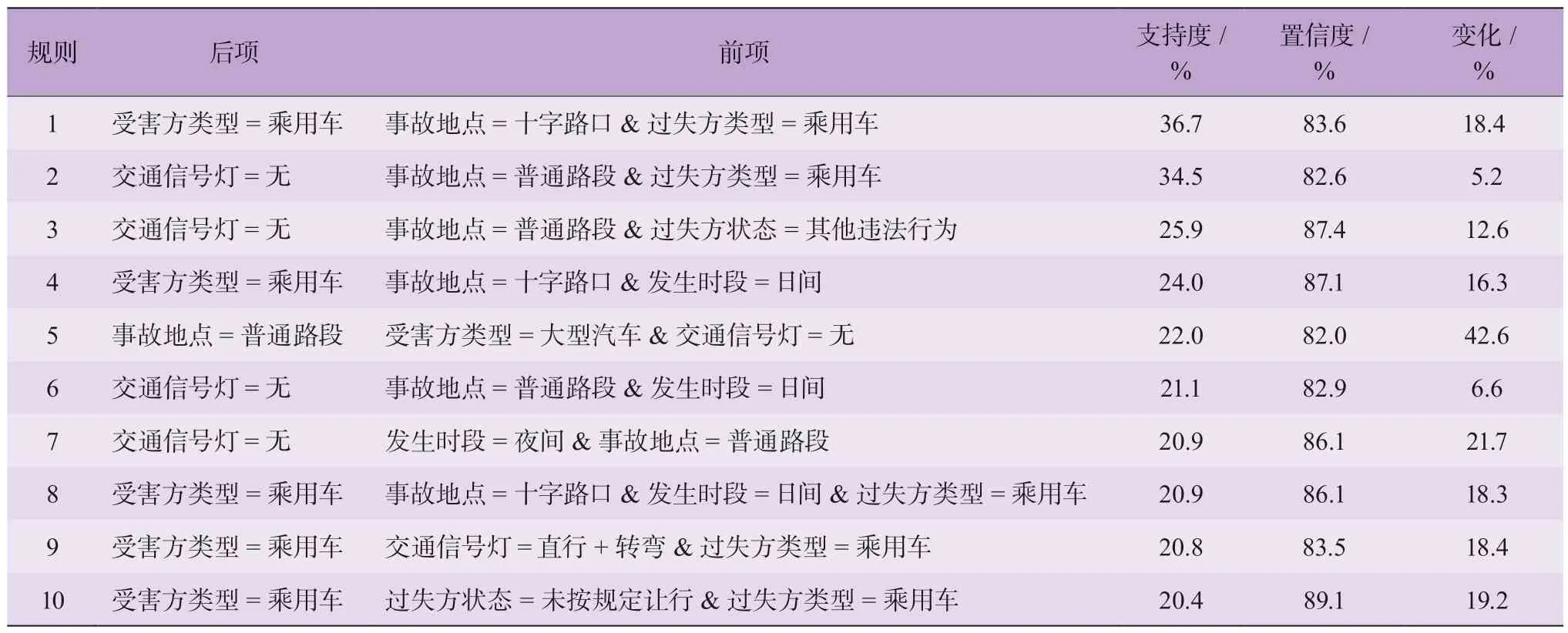
表3 高頻率與高耦合規則集對致死事故率的影響

4 結論

本文以NAIS 數據庫的雙車事故為樣本，利用Bayes 網絡和關聯規則方法，研究了V2V 事故嚴重程度的關鍵影響因素，以及關鍵因素的交互作用對致死事故率的影響。主要結論如下：

1）過失方車型、過失方狀態、受害方車型、發生時段、事故地點、交通信號燈等因素，是致死事故率的關鍵影響因素。

2）因素交互作用下，因素的聯合效應顯著，并且影響高于各自邊際效應和。過失方為大型汽車且處于超速行駛會提升55%的致死事故發生率，因此建議大型汽車強制裝配超速報警裝置；駕駛員在晨昏時段，要提高駕駛警惕。

3）在十字路口兩輛乘用車發生事故的頻率較高，但致死事故率相較于致死事故率的先驗概率會降低18.4%；大型汽車在無交通信號燈的普通路段發生事故，會提高42.6%的致死事故率。

4）數據采集的困難導致數據和字段有限，沒有充分考慮到車流量、汽車安全狀況和管理方面等因素，可能會對研究結果產生一定影響，有待進一步研究。