基于深度強化學習的高速公路換道跟蹤控制模型

李文禮，邱凡珂，廖達明，任勇鵬，易 帆

（1.重慶理工大學 汽車零部件先進制造技術教育部重點實驗室，重慶 400054，中國；2.重慶理工清研凌創測控科技有限公司，重慶 400054，中國）

高速公路行駛工況具有車速快、車輛多等特點，駕駛員很容易在換道時操作失誤，導致碰撞事故發生。根據數據統計，在中國大陸，換道引發的交通事故約占總事故的10%[1]，因此對高速公路換道行為進行控制是智能汽車控制技術中尤為重要的一部分。其中換道路徑的規劃是能否高效安全完成換道任務的前提和基礎；對換道路徑的精準跟蹤則是成功換道的關鍵，許多學者對這2 個方面進行了深入研究。

車輛換道路徑規劃方法主要分為基于搜索、概率、幾何等[2]。基于搜索和概率的方法存在實時性較差的缺點，在對實時性要求較高的自動駕駛領域中使用較少。而基于幾何的方法使用參數化曲線描繪軌跡，規劃結果直觀、精確，運算量相對更少。

WANG Chang 等人[3]針對車道變換過程采用七次多項式車道變換模型對車輛進行控制，結果表明該模型適用于不同速度的車道變換軌跡規劃。楊剛等人[4]基于五次多項式函數設計換道曲線，將軌跡參數求解問題轉化為約束設計和解目標函數問題，通過設計優化指標確定換道軌跡，取得了良好的效果。閆堯等人[5]為了追求換道過程中的舒適性和平穩性，利用五次多項式換道軌跡方法，同時建立了平均曲率最小、曲線長度最短的多目標函數，規劃出了智能車輛的最優軌跡。

在路徑跟蹤決策控制方面，常用的方法包括基于規則與基于學習[6]。基于規則的方法主要參考專家經驗或交通規則，結合具體場景進行合理控制，但缺乏靈活性，在動態變化的復雜交通行駛場景下無法很好控制。基于學習的方法則是通過離線學習復雜場景中的駕駛員數據信息獲得合理駕駛策略，然后直接利用從當前駕駛環境中感知到的信息輸出控制指令給車輛，使車輛更接近人類駕駛特性行駛。對于換道路徑跟蹤決策控制來說，由于換道過程屬于連續狀態的動作，可采用深度強化學習的方法，利用深度神經網絡對連續狀態空間下的決策問題進行處理，從而達到從傳感器輸入到執行器輸出的端到端控制。WANG Pin 等人[7]提出了一種基于深度Q 網絡(deep Q-network,DQN)算法的強化學習方法，訓練車輛完成自動變道行為控制，獲得了高效、平穩、安全的最佳變道駕駛策略。賀伊琳等人[8]針對軌跡跟蹤過程中橫向控制問題，提出了一種基于深度確定性策略梯度(deep deterministic policy gradient，DDPG)算法的智能車輛軌跡跟蹤方法，通過驗證表明基于DDPG 方法所用學習時間較短，跟蹤誤差較小。裴曉飛等人[9]針對連續動作空間下的自動駕駛換道決策，采用雙延遲深度確定性策略梯度(twin delayed deep deterministic policy gradient，TD3)算法，考慮安全性、行車效率和舒適性等因素構建了自主換道模型。

綜上，本文基于深度強化學習DDPG 算法研究高速行駛場景下智能車輛換道過程。首先利用五次多項式搭建換道路徑模型并建立跟蹤誤差函數，然后將車輛與規劃的換道路徑之間的跟蹤過程描述為試錯式深度強化學習過程，將車輛三自由度動力學模型融入深度強化學習環境中，與深度強化學習主體Agent 進行交互并傳遞自車與規劃的五次多項式換道路徑之間的橫向誤差、橫擺角角誤差等信息，主體以DDPG 算法進行更新，構造相應的Actor-Critic 神經網絡，輸出換道前輪轉角信息，完成對換道軌跡跟蹤過程中期望前輪轉角的學習，實現車輛換道決策控制。最后通過Matlab/ Simulink 搭建上述換道決策模型，并構建相應場景對決策模型的性能進行測試，驗證了該換道控制模型的有效性。

1 深度強化學習及換道場景概述

1.1 深度強化學習

深度強化學習是深度學習與強化學習結合的產物，既具有深度神經網絡的特征提取能力又包含強化學習的決策優勢，能基于深度神經網絡解決從感知到決策控制的端到端學習[10]。

強化學習方法通過與環境交互進行試錯學習，使模型自主探索得到控制系統最優決策，其基本模型框架用Markov 決策過程(Markov decision process,MDP)來描述[11]。Markov決策過程，可用表示環境狀態空間S、行為動作空間A、狀態轉移概率函數P、獎勵回報函數R的四元組＜S,A,P,R＞來刻畫。強化學習問題最終目的是求解模型最優策略，在該策略下能得到最大累積獎勵期望值。引入值函數用于判斷策略的優劣，包括狀態值函數和動作值函數。求解值函數有基于表格的和基于數值的2 種函數逼近方法。前者是構造一張表格，其中，將狀態值作為行、將動作值作為列，通過持續循環迭代更新表中的數值，但狀態空間集合較大時求解難度增大。因此基于值函數即通過深度神經網絡逼近最優值函數獲得最優控制策略的方法應用越來越廣泛。

1.2 車輛高速換道場景

根據換道動機和周圍環境影響因素，換道行為可分為強制換道和自由換道2 種，其中自由換道是為了更好的駕駛環境和更高的駕駛效率而進行換道操作。在高速公路場景中以自由換道比較常見，所以本文只針對自由換道行為進行研究。介于車輛換道行為主要發生在低密度交通流行駛過程中，本文只考慮處于交通流密度較低的高速公路雙車道平直路面環境中，前方車輛緩行時本車向左側變道情況。

圖1 為高速公路換道場景示意圖。

圖1 高速公路雙車道換道場景示意圖

車輛從當前行駛車道初始位置A向左駛入目標車道并最終換到目標位置B。當橫向位移達到車道寬度W時視為換道完成。根據我國的公路建設行業標準，取車道寬度W=3.75 m。

對高速行駛車輛做以下簡化：

1)x軸方向保持勻速行駛；

2) 當開始換道時不受其他車輛干擾；

3) 由于高速自主換道速度較高，換道過程中航向角較小，因此假設車輛橫向與縱向速度間影響忽略不計。

2 基于深度強化學習車輛高速換道模型

2.1 換道路徑模型

車輛在高速公路場景下的換道路徑模型首先需要選擇換道軌跡線型。換道軌跡需要滿足以下要求：

1) 滿足實際駕駛情形，并是可以實現的；

2) 一階、二階導函數需要連續可導；

3) 軌跡變化平穩且光滑。

在關于換道軌跡的研究中，較多使用多項式曲線作為換道軌跡。多項式曲線具有計算量小、軌跡光滑、曲率連續、適應性強、可靠性高等優點，而且只需要知道車輛換道的初始和結束時刻的運動狀態，可適用于復雜交通狀況下的換道軌跡規劃。在多項式換道軌跡中通常使用五次或七次多項式，多項式函數表達式為：

根據函數表達式對2 曲線的軌跡進行仿真對比，如圖2 所示。

由圖2 可知：五次多項式具有更小的橫擺角峰度以及更平滑的橫擺角變化，換道過程中產生的橫向加速度更小，具有更佳的穩定性和舒適度。本文采用五次多項式曲線對車輛換道進行換道軌跡的規劃，換道軌跡示意圖如圖3 所示。

圖2 多項式換道軌跡對比

圖3 換道軌跡示意圖

假設換道初始位置和結束位置均在車道中心線上，換道起始點縱向位置設為x(t0)，起始橫向位置為y(t0)，經過橫向位移W，縱向位移D完成換道后恢復直線行駛，換道終止時車輛的縱向位置設為x(te)，橫向位置為y(te)。根據換道過程知換道軌跡曲線函數應滿足以下條件：

式中：vx0為車輛初始時刻的縱向速度，vxe為結束時刻的縱向速度，t0為換道開始時刻，te為換道持續時間即終止時刻。

將上式代入(1)可得五次多項式系數ak，即：

由此可得換道參考路徑的側向位置y關于換道縱向總位移D、換道橫向總位移W、換道參考路徑的橫向位置坐標x的表達式：

根據換道過程中縱向速度不改變的假設，即vx0=vxe=vx，上式可表示為關于換道時間t的曲線函數（其中td為換道過程總時間）：

2.2 跟蹤誤差函數

完成五次多項式換道路徑規劃后需要對參考路徑進行跟蹤，涉及到橫向軌跡跟蹤時主要通過橫向位置偏差ey和橫擺角速度偏差eε進行跟蹤[12]，因此構建對應的換道路徑跟蹤誤差函數。根據安裝在車輛上的傳感器等設備獲取當前的車輛位置信息，通過對比參考路徑在當前時刻下橫向位置信息可計算出橫向位置偏差。考慮到在換道過程中并沒有一條實際道路，無法直接通過攝像頭獲得道路曲率，因此通過規劃的參考路徑曲率來代替實際道路曲率[13]，進而求出期待橫擺角速度。

若令：vy為車輛橫向車速，ay為車輛橫向加速度，f代表參考路徑的某一點，表示參考路徑在某一點的導數；則由上述換道參考路徑表達式計算出待追蹤的五次多項式路徑的曲率為

結合車輛縱向速度和道路曲率可求出期望橫擺角速度γrel=vx ρ，再通過對比車輛當前時刻的橫擺角速度可以獲得橫擺角速度偏差eε。

2.3 換道路徑跟蹤控制模型

結合換道路徑跟蹤誤差函數，采用DDPG 算法控制自動駕駛車輛完成換道路徑的跟蹤，實現換道駕駛過程，跟蹤控制模型總體算法框架如圖4 所示。

圖4 換道跟蹤決策控制算法框架

算法框架包括強化學習訓練和應用驗證過程：在強化學習訓練過程中，強化學習智能體作為控制器，通過輸出被控車輛的前輪轉角進而控制車輛跟蹤換道軌跡。換道過程中的車輛位置信息和五次多項式參考路徑信息輸入給跟蹤模型擬合出強化學習狀態信息St輸出給智能體，同時根據輸出的信息構建獎勵函數，智能體綜合狀態信息和回報值根據訓練策略做出控制動作At控制車輛調整運動狀態，此時車輛位置信息發生變化，進入下一控制狀態St+1,回報函數根據上一狀態值做出的動作所獲得的反饋信息進行評估并更新獎勵Rt+1，智能體更新策略并最終獲取最佳控制策略。訓練結束后進行應用驗證，將最佳控制策略輸出給決策層，并根據感知層中本車的運動狀態和生成的換道軌跡等狀態信息輸出動作，控制車輛完成換道過程。

2.3.1 車輛動力學模型

對于換道路徑跟蹤控制首先需要建立被控制對象的車輛動力學模型，而換道路徑的跟蹤控制主要關注車輛的側向運動和位姿，因此搭建了僅考慮沿y軸的側向運動、繞z軸的橫擺運動和沿x軸的側傾運動的三自由度簡化車輛動力學模型[14]。

根據Newton 第二定律得出汽車動力學方程為

式中：Iz為車輛繞軸的轉動慣量；lf和lr分別為質心到前、后軸的距離；δf為車輛前輪轉角；為車輛橫擺角；Cf、Cr分別為前后輪輪胎剛度。

根據上述公式建立車輛動力學模型，其中：Cf、Cr、lf、lr為車輛參數，當輸入前輪轉角δf后，可得，車輛當前的橫向速度Vy、橫向加速度ay、橫擺角ψ等信息。

2.3.2 Markov 決策過程建模

1) 狀態空間。

狀態空間是用來幫助自動駕駛汽車確定做出決策后發生的情況，所選取的狀態量需要全面反映當前時刻下車輛的所有特征值[15]。在車輛換道軌跡跟蹤控制中的狀態量主要包括車輛與規劃換道軌跡之間的橫向誤差ey、橫擺角速度偏差eε以及兩者的積分值和跟蹤路徑曲率ρ，除此之外還包括通過自車傳感器所獲取的當前時刻下相對起始點的橫向位移dy、自車橫向速度vy、橫向加速度ay。其狀態空間定義為

式中：ey為車輛與規劃換道軌跡之間的橫向誤差，eε為橫擺角速度偏差，t為時間，ρ為跟蹤路徑的曲率，dy為當前時刻相對起始點的橫向位移，vy為自車橫向速度，ay為橫向加速度。

2) 動作空間。

動作空間中包含被控制車輛所需要執行的動作指令，在換道路徑跟蹤過程中主要是通過控制車輛的橫向運動完成對路徑跟蹤的目的，因此動作空間為被控車輛的前輪轉角δf。控制器結合上述的三自由度車輛動力學模型，將強化學習輸出的前輪轉角轉化為車輛參數vx、vy、ψ的改變，車輛的位置信息(x,y)隨之發生改變。其動作空間定義為

3) 獎勵函數。

獎勵函數的設置可引導智能體與環境的交互，使輸出的動作決策能夠接近最佳策略，在換道路徑跟蹤控制中獎勵函數的設計用于調整輸出的前輪轉角動作值。換道路徑跟蹤的目標在于跟蹤精準性、換道高效性、行駛舒適性，因此基于這幾個方面設計獎勵函數。

針對跟蹤精準性，可根據橫向位置偏差ey和橫擺角eε速度偏差來評價，將橫向位置偏差和角偏差的計算總和作為基礎設計跟蹤精準獎勵函數Rf。當ey誤差減小到0.05 m 以內時給予正值獎勵H，當誤差大于0.1 m 時給予懲罰，鼓勵車輛減小與參考路徑在橫向和橫擺角之間的誤差值。令ω1、ω2、ω3分別代表各權重參數。精準性獎勵函數為

針對換道高效性，給予與橫向位移相關的正比獎勵Re。鼓勵車輛盡快完成換道過程，保證行車效率，當時間大于1 s 時若車輛的橫向位移仍為0 則給予懲罰P，使自動駕駛車輛在規定時間能完成換道過程。高效性獎勵函數為

式中，P為懲罰值。當運行時間大于1 s 時判斷車輛的橫向位移是否為0，若為0 則給予懲罰，若不為0 則隨著橫向位移增加，正比獎勵值增大。

針對舒適性，前輪轉向角越小，變化越平穩，換道行為決策舒適性也越好，因此基于前輪轉角設計舒適性獎勵函數Rc。舒適性獎勵函數為

最終綜合獎勵函數為

其中，M為模型懲罰。

另外，對控制過程設置終止條件，當滿足自車相對于初始位置橫向位移|dy|=3.75 m 或橫向位移偏差|ey|＞1 m 時，終止當前回合，進入下一回合，并重新配置環境狀態值；同時在觸及終止條件時，給予模型懲罰M，以防止橫向誤差過大。

2.3.3 基于DDPG 算法的路徑跟蹤控制模型

對換道路徑跟蹤設計了基于DDPG 算法的控制模型，其中強化學習主體使用DDPG 算法更新策略。DDPG 算法屬于異步策略算法中的一種,是基于Actor-Critic 框架的無模型算法，其網絡結構如圖5所示。

圖5 DDPG 網絡結構圖

Actor-Critic 框架包括了Actor 和Critic 2 個神經網絡。Actor 網絡依據環境給出的狀態觀測量S預測出一個決策動作A，環境根據給出的動作計算出獎勵r并產生一個新的狀態；Critic 網絡根據當前的狀態量S和動作值A計算出獎勵Q，然后通過Q更新Actor 網絡的策略函數參數θμ，Critic 網絡的參數θQ則根據智能體的獎勵函數進行更新,通過循環迭代最終訓練出最佳Actor 網絡和最佳決策動作值。

為了解決采樣樣本相關性問題，算法使用一個經驗回放池用于儲存之前的動作狀態轉移序列(St,At,Rt+1,St+1)，在梯度更新時隨機地從經驗池中抽取交互的樣本。

為了克服網絡更新不穩定的問題，DDPG 算法分別復制在線策略Actor 網絡μ'和在線價值Critic 網絡Q'作為其更新目標稱為目標網絡，在訓練完一個小批量的數據后，通過軟更新算法目標網絡的參數。

另外，在探索訓練過程中引入了隨機OU (Ornstein-Uhlenbeck，奧恩斯坦-烏倫貝克)噪聲N，將動作的決策過程從確定性變為一個隨機過程μ’(S)，再從這個隨機過程中采樣得到動作的值

對換道路徑跟蹤控制模型而言，DDPG 算法對神經網絡進行學習更新的過程如下：

1) 主網絡中的Actor 網絡在狀態量St下根據加入隨機噪聲的策略做出動作At并通過執行器控制車輛與環境交互進入下一狀態量St+1及產生當前動作的價值Rt+1；

2) 將產生的樣本數據(St,At,Rt+1,St+1)儲存到經驗回放池中，當存儲一定數量的樣本數據之后從中隨機采樣小批量樣本數據(Si,Ai,Ri+1,Si+1)；

3) 將目標動作和下一狀態量共同作為目標網絡中的Actor 網絡的輸入得到目標值Q'然后根據公式得到目標回報值

式中，γ表示折扣因子；

4) 通過最小化損失函數更新主網絡的Critic 網絡參數，將Si，Ai共同作為Critic 網絡的輸入得到實際值Q然后根據誤差公式得到Critic 網絡的誤差，然后通過最小化誤差對網絡進行更新

5) 通過策略梯度△θμJ更新主網絡的Actor 網絡參數；

6) 采用滑動平均的方式對目標網絡的Actor 和Critic 網絡進行軟更新，其中更新參數τ＜＜1：

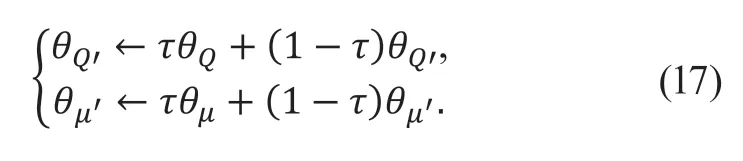
3 模型仿真與分析

為了驗證所提出基于深度強化學習的換道跟蹤決策控制模型的有效性，本文利用MATLAB/Simulink仿真平臺，采用DDPG 算法結合Simulink 中Agent 模塊構建仿真環境，對智能車輛換道過程的路徑跟蹤過程進行仿真與分析。

3.1 仿真環境設置

強化學習仿真訓練時采用的車輛模型參數如表1所示，根據車輛高速換道場景參數定義搭建仿真場景，設定在訓練過程中被控車輛的初始位置固定為(0,0) m，縱向初始速度在15～30 m/s 之間隨機取值，設定每個片段的仿真時間Tf=4 s，采樣時間周期Ts=0.05 s，強化學習訓練過程中的其他超參數如表2 所示，所有超參數的設置參考文獻[8]及文獻[15]并經過多次實驗經驗調整確定。

表1 智能車參數

表2 訓練超參數

3.2 仿真模型的搭建

在MATLAB 中設計好DDPG 網絡及仿真環境后，需在Simulink 中搭建基于DDPG 算法的換道跟蹤控制仿真模型，設置被控車輛的位置和運動參數，與Agent交互狀態、動作和獎勵。仿真系統框圖如圖6 所示。

圖6 仿真模型框架

路徑生成模塊根據每次隨機的速度結合五次多項式生成換道路徑并輸出每個時刻下的縱向坐標值和橫擺角給跟蹤誤差函數，結合車輛位姿信息和參考路徑信息計算出橫向誤差和角偏差，將跟蹤控制器分析狀態觀測值，根據訓練好的跟蹤策略輸出車輛前輪轉角對車輛進行換道跟蹤控制，最終完成換道過程。動作值的獎罰信息會反饋給控制器，用于評價控制效果。

3.3 模型仿真測試及結果分析

3.3.1 模型訓練

DDPG 算法學習過程中主要通過回合獎勵和平均獎勵值來反映訓練的收斂水平和學習效果。圖7 為該控制模型整個訓練過程中的獎勵值變化及最后100 個回合的獎勵值變化。平均獎勵值越高控制效果越好，實驗過程一共進行了350 個回合的訓練。在訓練剛開始的階段，獎勵值較大且上下波動幅度較大，主要是由于此時智能體處于從零開始學習的過程，只是通過隨機選擇動作進行探索。隨著訓練回合數增加，獎勵值開始減小同時波動幅度逐漸減小，證明此時智能體開始學習利用之前探索到的經驗調整當前動作。在第33 回合左右及第64 回合左右時，獎勵值出現一些幅度較小的波動，是由于DDPG 模型為了避免算法陷入局部最優解而加入了隨機噪聲的原因；在第93 回合左右之后波動又逐漸減小，在第117 回合左右之后獎勵值開始增大，這說明此時開始探索到更優的策略，控制效果逐漸變好。在250 回合之后獎勵值的波動趨于平緩，可以看出：此時算法基本收斂，智能體成功學習到換道路徑跟蹤的有效控制策略。

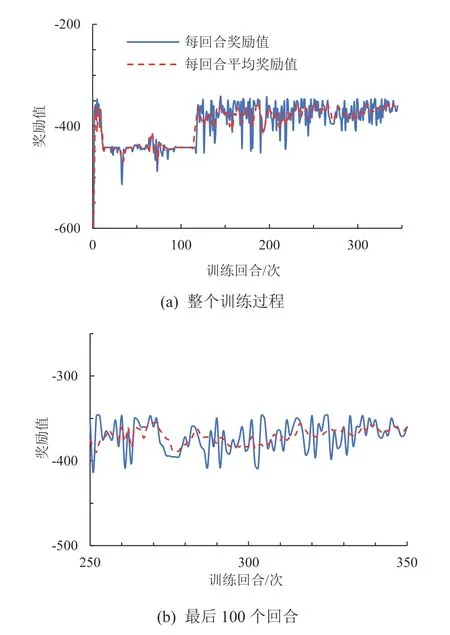
圖7 模型訓練獎勵值變化情況

3.3.2 模型測試結果及分析

為了驗證所設計的換道控制模型的可靠性及有效性，本文利用Matlab/Simulink 搭建控制模型仿真系統，建立對應的高速換道場景，分別采用所提出的基于DDPG 算法和MPC(模型預測控制)算法[16]，分別選擇初始車速60、100 km/h 對自動駕駛車輛換道路徑進行跟蹤，對仿真結果對比與分析。結果如圖8-圖13 所示。對于換道軌跡跟蹤控制系統來說，控制目標是通過靈活調整前輪轉角的控制量來不斷減少跟蹤軌跡與參考軌跡的誤差，主要包括橫向位置誤差和角誤差，要求車輛在換道過程中減小橫向位置誤差并且穩定角偏差。

圖8 和圖11 分別是60 km/h 低速和100 km/h 高速下橫向位置跟蹤值與規劃參考值的對比圖，

圖8 60 km/h 車速下橫向位置的跟蹤值與規劃參考值

圖9 60 km/h 車速下橫擺角的跟蹤值與規劃參考值

圖10 60 km/h 車速下側向加速度

圖11 100 km/h 車速下橫向位置的跟蹤值與規劃參考值

圖9 和圖12 分別為60 km/h 低速和100 km/h 高速下橫擺角跟蹤值與規劃參考值的對比圖。從圖中看出：當低速情況下時2 種方法控制的橫向誤差絕對值的最大值分別接近5、35 cm；橫向誤差絕對值的最小值接近于0；角偏差絕對值最大值分別接近2、16 mrad，說明在低速情況下2 種方法均能完成對換道軌跡的跟蹤。在高速情況下2 種方法控制的橫向誤差絕對值的最大值分別為0.12 m 和0.35 m 左右；角偏差絕對值最大值為10 mrad 和70 mrad 左右，可以看出DDPG 控制的橫向位置誤差絕對值相對更小，說明在高速的情況下所設計的控制系統基本可以準確跟蹤參考軌跡，僅在換道開始的過程相對于參考路徑有一定滯后，但考慮到車速較高，跟蹤誤差在可接受的范圍內。而采用MPC控制方法在換道過程中產生了較大的橫向偏差和角偏差，對換道路徑的跟蹤效果不佳。同時，DDPG 控制方法仿真時間較短，在3.2 s 時達到側向位移3.75 m完成換道過程，而MPC 控制方法的仿真時長稍長，證明所提出的方法在高速情況下換道更具高效性，能在更短時間內完成換道過程。

圖12 100 km/h 車速下橫擺角的跟蹤值與規劃參考值

另外，圖10 和圖13 為換道過程中側向加速度變化值對比圖。從中可以看出：DDPG 控制下整個仿真過程中車輛側向加速度變化率保持在一定范圍內，保證了換道過程中駕駛員的舒適性，而MPC 方法控制在高速換道情況下時側向加速度變化較大，可能會產生過大的轉角而導致乘員產生不適感。

圖13 100 km/h 車速下側向加速度

綜上所述，在車輛速度較低時DDPG 控制方法和MPC 控制方法均能很好地對換道軌跡進行跟蹤，但在高速情況下DDPG 控制方法相對MPC 控制方法具有更高的跟蹤精度和跟蹤穩定性，并且保證了換道的高效性和舒適性。

4 結論

本文基于深度確定性策略梯度算法，利用五次多項式建立換道路徑并給出跟蹤誤差函數，結合車輛三自由度動力學模型及深度強化學習框架設計搭建了一種高速換道路徑跟蹤控制模型。通過Markov 決策過程建立模型的狀態空間、動作空間、獎勵函數及終止條件，保證換道路徑跟蹤過程的精確性、高效性和舒適性。利用通過DDPG 算法進行更新的2 個神經網絡對車輛輸出動作進行調整，實現了對五次多項式換道路徑跟蹤控制策略的學習。將學習到的最優策略在設計的高速換道場景下進行驗證。

結果表明：本文提出的控制方法在100 km/h 的高速情況下橫向位置誤差絕對值的最大值接近0，角偏差絕對值最大值為10 mrad，車輛側向加速度變化保持在1 m/s2范圍內，既保證了換道軌跡跟蹤精度，同時具有良好舒適性。