基于MEMS陣列的二級(jí)融合降噪算法

梁思遠(yuǎn)，武嘉銘

(西安郵電大學(xué) 通信與信息工程學(xué)院， 陜西 西安 710121)

航向姿態(tài)系統(tǒng)可以提供姿態(tài)角信息，包括俯仰角、橫滾角和航向角。航空電子系統(tǒng)、自動(dòng)駕駛系統(tǒng)和導(dǎo)航系統(tǒng)都需要基于準(zhǔn)確的姿態(tài)角才能保障系統(tǒng)的可靠運(yùn)行。航向姿態(tài)系統(tǒng)需要從外部獲取自身相對(duì)于導(dǎo)航坐標(biāo)系的線加速度和角速度。首先，當(dāng)獲取角速度時(shí)利用航姿系統(tǒng)計(jì)算出姿態(tài)角，更新從載體系到導(dǎo)航坐標(biāo)系的方向余弦矩陣(Direction Cosine Matrix,DCM)。其次，基于當(dāng)前時(shí)刻的DCM將載體系的線加速度轉(zhuǎn)換到導(dǎo)航系。最后，對(duì)導(dǎo)航系的線加速度進(jìn)行數(shù)值積分，根據(jù)載體的初始速度和位置可以得到當(dāng)前時(shí)刻的速度和位置信息。

航向姿態(tài)系統(tǒng)的誤差主要由導(dǎo)航信息的初始值、數(shù)值計(jì)算過程和慣性器件的誤差引起的。低成本MEMS陀螺儀憑借其優(yōu)勢(shì)在消費(fèi)電子領(lǐng)域得到廣泛的應(yīng)用，但其精度較低、隨機(jī)誤差大，難以滿足慣性級(jí)應(yīng)用的要求。航向姿態(tài)系統(tǒng)在進(jìn)行姿態(tài)解算時(shí)，需要對(duì)角速率進(jìn)行積分得到角增量，但在積分過程中，誤差會(huì)逐漸累積，最終導(dǎo)致姿態(tài)角的漂移。為了抑制陀螺儀的隨機(jī)誤差，文獻(xiàn)[1]提出了二級(jí)卡爾曼濾波，雖然通過兩個(gè)階段的濾波可以顯著降低陀螺儀的零偏漂移，但在濾波的第二階段需要加速度計(jì)和磁力計(jì)的輔助，導(dǎo)致了系統(tǒng)的冗余。文獻(xiàn)[2]采用一階自回歸模型(Autoregressive Model，AR)對(duì)角速率建模，改進(jìn)了最優(yōu)估計(jì)過程，降低了數(shù)據(jù)處理的復(fù)雜度，但該模型使用的是時(shí)不變參數(shù)，動(dòng)態(tài)性能較差。文獻(xiàn)[3-4]指出微機(jī)電(Micro Electro-mechanical Systems,MEMS)陀螺儀陣列中陀螺儀的數(shù)量一般有幾十個(gè)，雖然可以改善消費(fèi)級(jí)陀螺儀的噪聲特性，但喪失了體積和質(zhì)量上的優(yōu)勢(shì)。此外，基于神經(jīng)網(wǎng)絡(luò)[5-6]和支持向量機(jī)[7-9]等智能算法的降噪方法需要大量的樣本數(shù)據(jù)和訓(xùn)練時(shí)間。

針對(duì)傳統(tǒng)方法需要依賴高精度的模型，或者需要加速度計(jì)和磁力計(jì)的輔助，以及微機(jī)電陀螺儀精度較低、隨機(jī)誤差大的問題，擬提出基于最小方差和遞推最小二乘(Recursive Least Squares，RLS)的二級(jí)融合算法。首先，對(duì)MEMS陀螺儀信號(hào)進(jìn)行經(jīng)驗(yàn)?zāi)B(tài)分解(Empirical Mode Decomposition,EMD)，EMD分解后的各階分量可以認(rèn)為是平穩(wěn)的單分量，再采用小波閾值降噪的方法處理各階分量，基于最小方差和RLS對(duì)各階分量進(jìn)行二級(jí)融合。其次，與均值殘差分量疊加得到融合角速率參與航姿系統(tǒng)的解算。最后，通過仿真實(shí)驗(yàn)，驗(yàn)證所提算法的有效性。

1 基于MEMS陣列的冗余航姿系統(tǒng)

MEMS陀螺儀陣列系統(tǒng)包括陣列傳感器板和數(shù)據(jù)處理板，其中傳感器板由10個(gè)MPU9250組成，數(shù)據(jù)處理板的芯片是STM32H750。傳感器板和數(shù)據(jù)采集板通過接插件相連。陣列傳感器板將采集到的角速率等數(shù)據(jù)通過集成電路總線(Inter-Integrated Circuit,IIC)發(fā)送至數(shù)據(jù)處理板，數(shù)據(jù)處理板上集成了MEMS陣列融合算法，對(duì)各個(gè)陀螺儀的角速率數(shù)據(jù)進(jìn)行處理，最后輸出融合的角速率數(shù)據(jù)。

STM32H750是STMicroelectronics推出的基于ARM Cortex M7內(nèi)核的處理器，1 MB～2 MB的Flash，1 MB的靜態(tài)隨機(jī)存取存儲(chǔ)器(Static Random-Access Memory,SRAM)，最高運(yùn)行頻率可達(dá)400 MHz，擁有豐富的輸入輸出(Input/Output,I/O)接口[10]。MPU9250是InvenSense公司推出的9軸運(yùn)動(dòng)處理組件，為一款常見的消費(fèi)級(jí)MEMS。MPU9250內(nèi)部集成有3軸陀螺儀、3軸加速度計(jì)和3軸磁力計(jì)，輸出都是16位數(shù)字量，可以通過IIC接口和單片機(jī)進(jìn)行數(shù)據(jù)交互，傳輸速率最高可達(dá)400 kHz·s-1。陀螺儀的角速度測(cè)量范圍最高可達(dá)±2 000°/s，具有良好的動(dòng)態(tài)響應(yīng)特性。加速度計(jì)的最大測(cè)量范圍為±16 g，靜態(tài)測(cè)量精度高[11]。具體的基于MEMS陣列的冗余航姿系統(tǒng)如圖1所示。

圖1 基于MEMS陣列的冗余航姿系統(tǒng)

傳感器陣列采用正反布置，單面5個(gè)，MEMS陀螺儀的布局如圖2所示。

圖2 MEMS陀螺儀的布局

反面方向和正面一致，如慣性測(cè)量單元6(Inertial Measurement Unit,IMU6)在IMU1的背面，方向一致；IMU7在IMU2的背面，方向一致，等等。陣列中IMU1和IMU2、IMU3、IMU4、IMU5的夾角分別為90°、180°、270°和0°，反面陣列中的IMU方向夾角與正面相同。以IMU1的坐標(biāo)軸朝向作為整個(gè)MEMS陣列組合輸出的坐標(biāo)基準(zhǔn)。

2 MEMS陣列的融合算法

2.1 MEMS陀螺儀陣列的誤差模型

角度隨機(jī)游走是MEMS陀螺儀的主要誤差源之一[12]，MEMS陀螺儀的誤差模型[13]可以表示為

y=ω+η

(1)

式中：y是MEMS陀螺儀的輸出角速率；ω是真實(shí)角速率；η是隨機(jī)噪聲，表現(xiàn)為角度的隨機(jī)游走。

于是,MEMS陣列的誤差模型可以表示為

Y=Iω+η

(2)

式中：Y=[y1y2…yn]T為輸出角速度矩陣，陣列中的每個(gè)陀螺是一致的；η=[η1η2…ηn]T表示隨機(jī)噪聲矩陣；I=[1 1 … 1]T表示陀螺儀的配置矩陣。

2.2 基于最小方差和最小二乘的二級(jí)融合算法

MEMS陀螺儀的信號(hào)具有弱非線性和弱非平穩(wěn)性。EMD分解具有自適應(yīng)的特點(diǎn)，且本征模式函數(shù)(Intrinsic Mode Function,IMF)分量是平穩(wěn)的單分量，便于進(jìn)行小波閾值降噪處理。基于最小方差對(duì)各階分量進(jìn)行融合，通過RLS估計(jì)得到各階最優(yōu)IMF分量。對(duì)殘差分量取平均，將各階分量和殘差分量直接疊加得到最終的融合信號(hào)。二級(jí)融合算法原理示意圖如圖 3所示。

圖3 二級(jí)融合算法原理示意圖

下面分別介紹二級(jí)融合算法示意圖中的信號(hào)EMD分解、最小方差權(quán)值的確定、最優(yōu)IMF遞推最小二乘估計(jì)和信號(hào)重構(gòu)等4個(gè)模塊。

2.2.1 信號(hào)的EMD分解

對(duì)MEMS陣列的陀螺儀信號(hào)進(jìn)行經(jīng)驗(yàn)?zāi)B(tài)分解，可以得到第m個(gè)MEMS陀螺儀的信號(hào)為

(3)

m=1,2,…,10

2.2.2 最小方差的權(quán)值確定

最小方差估計(jì)將估計(jì)量看作是觀測(cè)量的線性組合，以信號(hào)的最小方差為準(zhǔn)測(cè)求待定系數(shù)。噪聲方差小的信號(hào)加權(quán)系數(shù)大，噪聲方差大的信號(hào)加權(quán)系數(shù)小，避免了平均加權(quán)的不分優(yōu)劣的缺點(diǎn)。

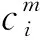
(4)

(5)

2.2.3 最優(yōu)IMF遞推最小二乘估計(jì)

最小二乘估計(jì)不需要任何先驗(yàn)知識(shí)，已知被估計(jì)量的量測(cè)模型即可實(shí)現(xiàn)信號(hào)參量的估計(jì)，且易于實(shí)現(xiàn)，同時(shí)能使誤差平方和達(dá)到最小。考慮最小二乘估計(jì)必須將所有的觀測(cè)數(shù)據(jù)同時(shí)處理，當(dāng)觀測(cè)數(shù)據(jù)很多時(shí)，其存儲(chǔ)和計(jì)算量都很大。因此，采用遞推的方法，不但可以減少計(jì)算和內(nèi)存消耗，還可以實(shí)現(xiàn)實(shí)時(shí)處理。

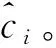
(6)

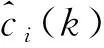
2.2.4 信號(hào)重構(gòu)

將經(jīng)過最小二乘融合和遞推最小二乘估計(jì)得到的各階IMF分量和均值殘差分量直接疊加，可以得到最終的信號(hào)重構(gòu)，其表達(dá)式為

(7)

重構(gòu)信號(hào)中的各個(gè)IMF分量是平穩(wěn)的，并且都經(jīng)過小波閾值降噪處理。同時(shí)，按照最小方差原則對(duì)各個(gè)陀螺儀的分量進(jìn)行加權(quán)，有效地抑制了隨機(jī)躁聲。因此，經(jīng)過降噪預(yù)處理的重構(gòu)信號(hào)在進(jìn)行姿態(tài)解算時(shí)可以提供更加準(zhǔn)確的姿態(tài)角。

3 姿態(tài)解算

(8)

式中：Q=q0+q1i+q2j+q3，k，i、j、k是虛數(shù)單位；ωx，ωy，ωz分別表示陀螺儀的3個(gè)軸的角速率。微分方程的求解可以采用雙子樣算法[17]，即

(9)

式中：C2=1-Δθ2/8，表示cosΔθ/2的二級(jí)泰勒展開；S2=1/2，表示sin(Δθ/2)/Δθ的二級(jí)泰勒展開。為了避免噪聲在微分時(shí)放大，應(yīng)直接用角增量確定四元數(shù)。Δθx(tn),Δθy(tn)和Δθz(tn)分別為陀螺儀3個(gè)軸的角增量及陀螺儀合角增量，表達(dá)式分別為

考慮計(jì)算誤差等因素，計(jì)算過程中四元數(shù)會(huì)逐漸失去規(guī)范化特性。因此，若干次更新后，必須對(duì)四元數(shù)做規(guī)范化處理，表達(dá)式為

(10)

其中

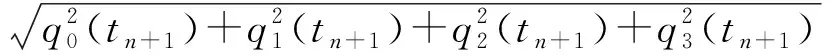
假設(shè)載體的航向角為ψ，俯仰角為θ和橫滾角為γ，姿態(tài)矩陣中的元素用ψ、θ和γ，則姿態(tài)矩陣元素可以分別表示為

T11=cosγcosψ+sinγsinψsinθ
T12=sinψcosθ
T13=sinγcosψ-cosγsinψsinθ
T21=-cosγsinψ+sinγcosψsinθ
T22=cosψcosθ
T23=-sinψsinγ-cosγcosψsinθ
T31=-sinγcosθ
T32=sinθ
T33=cosγcosθ

從姿態(tài)矩陣的元素中可以提取出俯仰角、橫滾角和航向角，其表達(dá)式為

(11)

4 實(shí)驗(yàn)驗(yàn)證與結(jié)果分析

4.1 Allan方差分析

Allan方差分析法常用于分析陀螺儀的隨機(jī)誤差。陀螺儀誤差的Allan方差分析結(jié)果可以表示為

(12)

式中：Q表示量化噪聲；N表示角度隨機(jī)游走；B表示零偏不穩(wěn)定性；K表示角速率隨游走；R表示速率斜坡。

使用加權(quán)最小二乘進(jìn)行多元線性回歸分析，確定出各種噪聲誤差系數(shù)Ak，即

(13)

各噪聲項(xiàng)和誤差系數(shù)的對(duì)應(yīng)關(guān)系，誤差系數(shù)和Ak的轉(zhuǎn)換關(guān)系如表1所示。

表1 誤差系數(shù)與Ak的轉(zhuǎn)換關(guān)系

將航姿系統(tǒng)固定在單軸轉(zhuǎn)臺(tái)上，陀螺儀采樣率設(shè)定為100 Hz，室溫條件下采集數(shù)據(jù)1 h，分析數(shù)據(jù)的Allan方差并繪制雙對(duì)數(shù)圖如圖4所示。從Allan方差的雙對(duì)數(shù)圖可以看出，斜率主要表現(xiàn)為-1/2和0，說明陀螺儀主要受角度隨機(jī)游走和零偏不穩(wěn)定性的影響，陀螺儀Allan方差對(duì)比情況如表2所示。

圖4 陀螺儀數(shù)據(jù)的Allan標(biāo)準(zhǔn)差分析

表2 陀螺儀Allan方差對(duì)比

所提算法將陀螺儀原始數(shù)據(jù)的角度隨機(jī)游走降低了約68%，卡爾曼濾波算法將原始數(shù)據(jù)的角度隨機(jī)游走降低了約19%。二級(jí)融合算法將陀螺儀原始數(shù)據(jù)的零偏不穩(wěn)定性降低了約75%，卡爾曼濾波算法將零偏不穩(wěn)定性降低了約19%。

4.2 動(dòng)態(tài)性能分析

將航姿系統(tǒng)固定在單軸轉(zhuǎn)臺(tái)上進(jìn)行常規(guī)多速率實(shí)驗(yàn)，采樣率設(shè)定為100 Hz，通過串口將數(shù)據(jù)發(fā)送至上位機(jī)。分析俯仰角、橫滾角和姿態(tài)角的原始數(shù)據(jù)和經(jīng)過二級(jí)融合去噪的均方根誤差，姿態(tài)角均方根誤差如表 3所示。使用不同算法得到的姿態(tài)角變化曲線分別如圖 5、圖 6和圖 7所示。

表3 姿態(tài)角均方根誤差

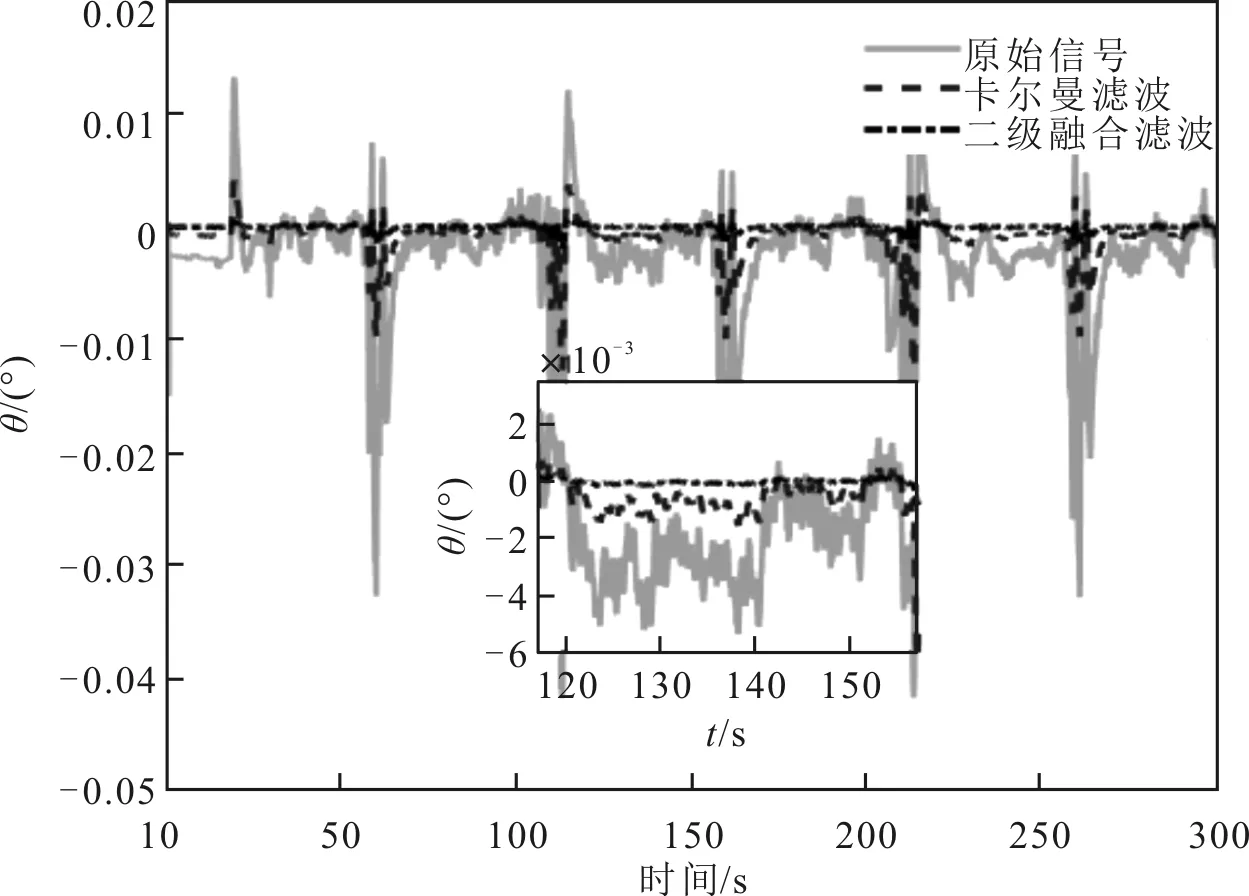
圖5 俯仰角變化

圖6 橫滾角變化

圖7 航向角變化

從圖5和圖6可以看出，經(jīng)過二級(jí)融合算法的處理，陀螺儀俯仰角和橫滾角的變化比較平穩(wěn)。在航向角發(fā)生變化時(shí)二級(jí)融合算法有效抑制了俯仰角和橫滾角的震蕩。從圖7可以看出，航向角在發(fā)生變化時(shí)，由于誤差的積累，導(dǎo)致航向角發(fā)生了漂移。點(diǎn)畫線表示經(jīng)過二級(jí)融合算法處理的航向角，當(dāng)航向角由0°變化至負(fù)180°時(shí)，漂移明顯減少，而且效果好于卡爾曼濾波算法。

5 結(jié)語(yǔ)

針對(duì)航姿系統(tǒng)中MEMS陀螺儀隨機(jī)誤差較大、精度較低的問題，提出了一種基于最小方差和遞推最小二乘的二級(jí)融合算法。該算法采用最小方差估計(jì)出最優(yōu)的IMF加權(quán)系數(shù)，再根據(jù)遞推最小二乘得到最優(yōu)IMF估計(jì)值，最后將各階分量和殘差疊加得到重構(gòu)信號(hào)。為了驗(yàn)證算法的有效性，在靜態(tài)和動(dòng)態(tài)環(huán)境下將二級(jí)融合算法和卡爾曼濾波算法進(jìn)行了比較。實(shí)驗(yàn)結(jié)果表明,卡爾曼濾波算法可以將角度隨機(jī)游走系數(shù)降低約19%，二級(jí)融合算法將角度隨機(jī)游走系數(shù)降低了約68%，二級(jí)融合算法與卡爾曼濾波算法相比顯著降低了陀螺儀的角度隨機(jī)游走系數(shù)；零偏不穩(wěn)定性經(jīng)過二級(jí)融合算法處理比卡爾曼濾波算法提高了約56%。在動(dòng)態(tài)性能分析中，所提算法將俯仰角、橫滾角和俯仰角的均方根誤差分別降低了約98%、98%和84%，比卡爾曼濾波的性能提高了約76%、76%和70%。