求解旅行商問題的聯合算子模擬退火算法

李昌興，黃 杉

(1.西安郵電大學 理學院,陜西 西安 710121；2.西安郵電大學 通信與信息工程學院,陜西 西安 710121)

模擬退火算法(Simulated Annealing Algorithm，SAA)不僅可以解決連續函數優化問題，也成功應用于求解組合優化問題[10]。對于組合優化問題，必須使用操作算子產生和接受新解。操作算子的策略非常重要，直接影響著模擬退火算法的優化性能[11]。在反序、移位和交換算子的基礎上，文獻[12]使用逆轉操作算子，文獻[13]使用強制隨機鄰域變換策略，這些操作算子改善了模擬退火算法的局部搜索能力。文獻[14]提出融合最近、最遠和隨機插入操作的統一插入操作和最壞刪除操作，通過自適應鄰域提高了搜索性能。文獻[15]提出自適應升溫控制策略，平衡了全局搜索與局部搜索的關系，獲得更好的全局優化能力。文獻[16]建立了模擬退火算法的弛豫時間模型，給出退火過程Markov鏈長度的理論估計，提出了Markov鏈的動態調整策略，對于模擬退火算法的參數選擇具有重要的理論指導意義。但是，以上研究并未充分利用不同操作算子的內在聯系與相互作用，導致模擬退火算法精度不足，性能不高。

針對模擬退火算法中操作算子的生成策略問題，研究反序、移位和交換算子的特征與相互關系，發現交換操作與反序操作在機理上具有等價關系。利用這種等價關系，擬提出一種新的交換/反序聯合算子(Joint Operator，JO)模擬退火算法，并利用不同規模的TSP問題對聯合算子進行仿真實驗。

1 模擬退火算法求解旅行商問題

1.1 模擬退火算法

模擬退火算法從較高的初始溫度出發，在當前解的鄰域不斷通過隨機擾動產生新的候選解，以一定的概率接受候選解。模擬退火算法包括內外兩重循環：外循環是溫度循環，控制退火溫度降低的過程；內循環是在每一溫度下迭代產生新解，循環次數也稱Markov鏈長度。

模擬退火算法的基本步驟如下。

步驟1隨機產生初始解X0。

步驟2在溫度Tk下進行Lk次循環迭代。由當前解Xold產生新的候選解Xnew，并按Metropolis接受準則，以一定的概率接受候選解Xnew作為當前解。候選解與當前解目標函數值的差ΔE及候選解的接受概率P的表達式分別為

ΔE=E(Xnew)-E(Xold)

(1)

(2)

式中：k表示溫度循環變量；E(Xold)表示當前解Xold的目標函數值；E(Xnew)表示新解Xnew的目標函數值。

Metropolis準則允許以一定的概率接受惡化解,使算法可以跳出局部最優解，是模擬退火算法能收斂于全局最優解的關鍵。

步驟3按照設定的退火控制策略緩慢降低退火溫度，直到達到溫度終值，完成退火過程，這時的當前解就是達到最低能量狀態的最優解。

1.2 求解旅行商問題的操作算子

模擬退火算法要從當前解的鄰域中產生新的候選解，解的表達形式和鄰域結構對算法收斂非常重要。組合優化問題中，目標函數不僅依賴于解的取值，而且與解的結構、次序相關。旅行商問題的路徑長度僅取決于解的排列次序，通常用城市編號序列表示問題的解。

為了滿足組合優化問題的約束條件，需要通過操作算子對當前解序列進行變換操作，改變某些點的排列次序產生新解。基本的操作算子是交換算子、移位算子和反序算子[1，11]。

交換算子是將當前路徑Snow中的第i個城市Ci與第j個城市Cj的位置交換，得到新路徑Sswap，當前路徑和新路徑的表達式分別為

Snow=C1…Ci-1(Ci)Ci+1…Cj-1(Cj)Cj+1…Cn

Sswap=C1…Ci-1(Cj)Ci+1…Cj-1(Ci)Cj+1…Cn

移位算子是將當前路徑Snow中的第i個城市Ci移動到第j個城市Cj之后的位置，得到新路徑Smove，當前路徑和新路徑的表達式分別為

Snow=C1…Ci-1(Ci)Ci+1…Cj-1(Cj)Cj+1…Cn

Smove=C1…Ci-1Ci+1…Cj-1(Cj)(Ci)Cj+1…Cn

反序算子是將當前路徑Snow中從第i個城市Ci到第j個城市Cj之間的城市排列順序反向翻轉，得到新路徑Sinv，當前路徑和新路徑的表達式分別為

Snow=C1…Ci-1(CiCi+1…Cj-1Cj)Cj+1…Cn

Sinv=C1…Ci-1(CjCj-1…Ci+1Ci)Cj+1…Cn

1.3 多個新解的競爭機制

模擬退火算法本質上是基于隨機搜索的優化方法，操作算子是模擬退火算法求解旅行商問題的核心機制。操作算子的運行策略不僅決定了新解的可行性，而且與獲得優質解的概率密切相關，影響著模擬退火算法的優化性能。

交換算子、移位算子和反序算子所產生的新路徑與當前路徑相比，分別有8段、6段、4段路徑的改變。隨著當前路徑的不斷優化，通過這些算子獲得更好路徑的概率越來越小。增大循環次數即Mar-kov鏈長度可以提高優化性能，但這也帶來了計算量的增大。

在每次循環產生的多個新解擇優使用的競爭機制，可以提高獲得更好路徑的概率。文獻[17]提出了多粒子模擬退火算法，每次擾動產生多個新解，選取最優者作為候選解。文獻[18]在每次循環中通過斷裂、倒置及重組操作產生6個新路徑，選擇最好路徑作為候選解。類似地，文獻[19]提出了多線程的并行算法，可以并行產生多個新解，從中找出最好的候選解。

引入產生多個新解的競爭機制，可以提高模擬退火算法的優化性能，但也增大一定的計算量。由于計算量的增長與新解個數的增加近似成正比，這與直接增大循環次數相比算法未必更為有效。只有在循環中產生多個新解，而又不增大計算量的前提下，才能真正提高模擬退火算法的總體性能。這就需要研究現有操作算子的運行特征與相互關系，構造同時產生多個新解的操作算子。

2 聯合操作算子

2.1 交換、反序和移位操作的關系

模擬退火算法由新解與當前解的目標函數差ΔE計算新解的接受概率。在旅行商問題中，使用交換算子、反序算子或移位算子產生新路徑時，并不需要直接計算新路徑的總長度E(Xnew)，可以通過不同變換操作的特征直接計算ΔE，以減少計算量。

交換操作的路徑差ΔEswap、反序操作的路徑差ΔEinv與移位操作的路徑差ΔEmove的表達式分別為

ΔEswap=[d(Ci-1,Cj)+d(Ci,Cj+1)]-
[d(Ci-1,Ci)+d(Cj,Cj+1)]+
[d(Cj,Ci+1)+d(Cj-1,Ci)]-
[d(Ci,Ci+1)+d(Cj-1,Cj)]

(3)

ΔEinv=[d(Ci-1,Cj)+d(Ci,Cj+1)]-
[d(Ci-1,Ci)+d(Cj,Cj+1)]

(4)

ΔEmove=[d(Ci-1,Ci+1)+d(Cj,Ci)+d(Ci,Cj+1)]-
[d(Ci-1,Ci)+d(Ci,Ci+1)+d(Cj,Cj+1)]

(5)

式中，d(Ci,Cj)表示城市Ci與Cj之間的距離。

對比這3種操作所產生的路徑差，可以發現具有很多相同的距離項。特別是式(4)反序操作的路徑差ΔEinv中的全部4段距離，都出現在式(3)交換操作的路徑差ΔEswap中，并且正負號也相同。因此，在計算式(3)交換操作的路徑差ΔEswap時，可以先計算式(4)中ΔEinv的4段距離，再計算剩下的4段距離。就能在計算ΔEswap的同時得到ΔEinv的值，并不增大計算量，同時還獲得了2條新路徑的ΔE。

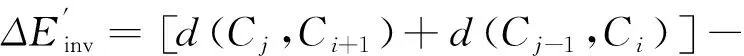
(6)

于是，交換操作的路徑差等于兩個嵌套的反序操作的路徑差之和，其表達式為

(7)

因此，可以將交換操作分解為兩步：先將當前路徑Snow中從城市Ci到城市Cj之間的城市排列順序反向翻轉得到新路徑Sinv；再將路徑Sinv中從城市Cj-1到城市Ci+1之間的城市排列順序再次翻轉，兩次翻轉后得到的路徑就是通過交換算子所得到的新路徑Sswap。第一步反向翻轉路徑Sinv和第二步反向翻轉路徑Sswap的表達式分別為

Sinv=C1…Ci-1Cj(Cj-1…Ci+1)CiCj+1…Cn
Sswap=C1…Ci-1Cj(Ci+1…Cj-1)CiCj+1…Cn

這說明交換操作等價于兩個嵌套的反序操作的疊加復合。

2.2 交換-反序聯合算子

3 實驗結果及分析

3.1 實驗方案

為檢驗提出的交換-反序聯合算子的優化性能，從 TSPLib 案例庫中選取 4 個不同規模的旅行商問題Eil51、Eil76、Eil101和Ch150作為測試案例，其城市數量分別為51、76、101、150，已知的最優路徑長度分別為426、538、629和6 528。

所提算法實驗環境為CPU：Intel(R)Core(TM) i5-4460S@2.90 GHz，內存為8 GB/1 600 MHz，操作系統為Window s7(64位/Service Pack 1)，采用 Python 3.8編程。

關于模擬退火算法的控制函數選擇，控制溫度按照Tk=αTk-1指數衰減，衰減系數取α∈(0.9,1.0)，按照式(2)Metropolis 準則接受新解。

考慮模擬退火算法的性能受到優化參數的影響，對每個測試案例分別采用不同的參數各進行兩組實驗。第1組參數為：初溫100，終溫1，衰減系數0.95，共90個溫度狀態，Markov鏈長度1 000；第2組參數為：初溫100，終溫1，衰減系數0.98，共228個溫度狀態，Markov鏈線性增大，平均鏈長1 000。由于模擬退火算法的優化結果有一定的隨機性，在每組參數下各做10次重復實驗，得到10次重復實驗的最小值、平均值、最大值，具體對比結果分別如表1至表4所示。

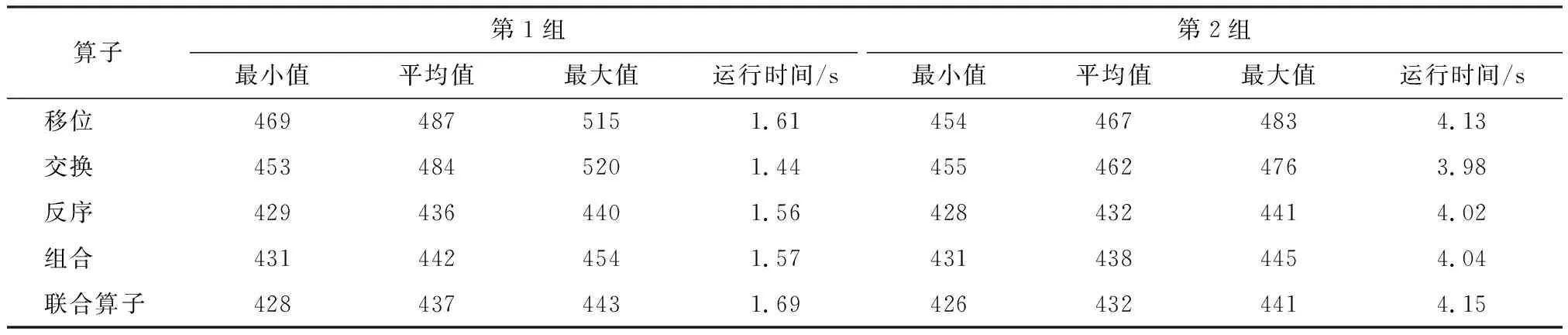
表1 Eil51問題實驗結果對比

表2 Eil76問題實驗結果對比

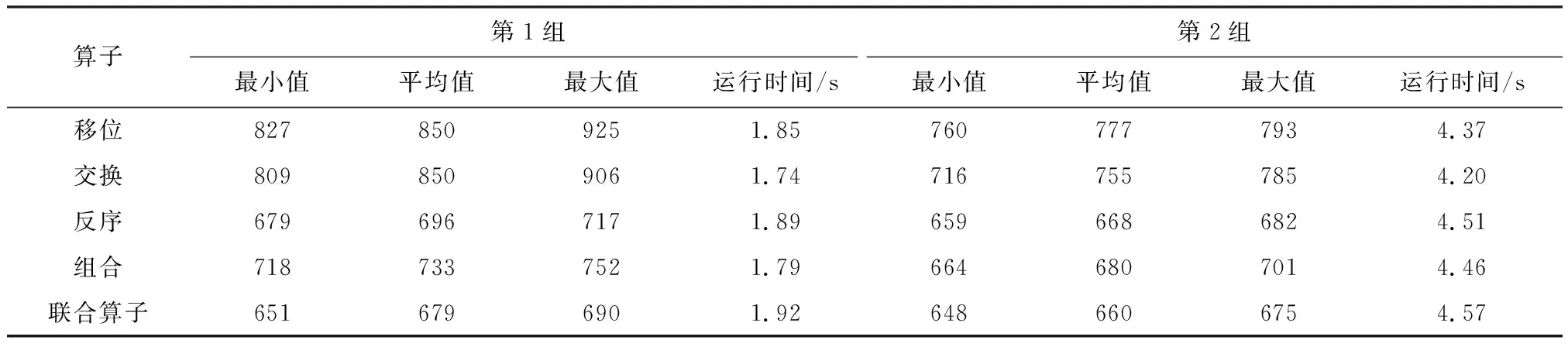
表3 Eil101問題實驗結果對比

表4 Ch150問題實驗結果對比

3.2 實驗結果的分析

對表1至表4所示的聯合算子模擬退火算法的優化結果與使用現有的移位、交換、反序算子以及組合移位/交換/反序算子的模擬退火算法的優化結果進行比較分析，可以得到4個不同規模的旅行商問題在不同測試參數下的結果。使用交換-反序聯合算子時最小值、平均值、最大值都是最好的，表明聯合算子的性能優于移位、交換、反序算子及其組合方案，這得益于聯合算子與其他算子相比的搜索數量更大。

使用聯合算子和現有算子的模擬退火算法在各自的第2組的性能比第1組都有所提高，但計算時間也都更長，且時間增大與Markov鏈長度大致成正比。這也意味著如果通過增大循環迭代次數改善性能，將會直接付出計算量成比例增大的代價。各種方案在相同參數下運行時間隨問題規模有所增大，但差異并不顯著，這是由于算法中僅計算路徑差，而不需要計算完整的路徑長度。因此，計算量與問題規模沒有太大關系。

在不同規模問題的測試中，聯合算子模擬退火算法優化性能提高的幅度不同。較小規模的問題，現有算子也已經獲得較好的結果，聯合算子提高性能的幅度不大；較大規模的問題，復雜程度高，現有算子的優化結果較差，而聯合算子提高性能的幅度較為顯著。

聯合算子模擬退火算法在Eil51問題找到了已知的最優路徑，在Eil76問題很接近已知的最優路徑，但對Eil101、Ch150問題的優化結果與已知的最優路徑還有2%～3%的誤差。這一方面說明大規模TSP問題的復雜程度更高，找到最優路徑需要更多的搜索；另一方面通過調整聯合算子的參數，還可以獲得更好的優化路徑。

在4個不同問題和兩組不同參數條件下，使用聯合算子的計算時間比使用其他算子時略有增大，但并不顯著，這與前文的分析是一致的。而聯合算子產生的新解數量是其他算子的3倍，遠高于計算時間的增大。

通過以上分析，聯合算子模擬退火算法不增加太多的計算量，而通過產生多個新解以增強搜索能力從而提高了算法的優化性能。

4 結語

分析了模擬退火算法操作算子的特征與相互關系，發現交換操作等價于兩個嵌套的反序操作的疊加復合。提出了一種新的交換-反序聯合算子，獲得由交換操作和反序操作所產生的3條新路徑，從中擇優作為新解。聯合算子既在循環中產生多個新解，又不增加過多計算量，提高了算法的優化性能。通過4個不同規模的TSP問題的實驗，驗證了聯合算子的性能優于現有的移位、交換、反序算子，也優于這些算子的組合方案。交換-反序聯合算子不僅可以用于模擬退火算法，也可以應用于其他進化算法，如遺傳算法、粒子群算法中的變異操作以擴展搜索空間。此外，交換與反序算子存在等價關系，其他操作算子之間也具有不同程度的相關性。對于揭示和利用這些相關性提高算法效率，將是后續研究工作的方向。