不等式約束最優化問題最優性條件的教學

孫敏，田茂英

（1.棗莊學院 數學與統計學院，山東 棗莊 277160；2.山東煤炭衛生學校 生理學教研室，山東 棗莊 277160）

最優性條件是最優化方法課程的教學重點.一方面，最優性條件給出了最優解滿足的必要條件，因此，通過求解最優性條件可以得到可能的最優解，從而將搜索范圍從可行域縮小到有限個穩定點或KKT點；另一方面，最優性條件在最優化問題的算法設計中起著關鍵作用.實際上，很多最優化算法的迭代格式、終止條件等的設計動機來自于最優性條件[1-5]，如增廣拉格朗日乘子法中乘子迭代格式的設計，可分裂凸規劃的交替方向法對偶變量迭代格式的設計等.最優性條件在很多領域有著廣泛的應用，是很多機器學習問題分析的必要方法[6-7].

最優性條件是最優化方法課程的教學難點.在學習高等數學多元函數約束極值問題時，通過引入拉格朗日函數，將含等式約束的優化問題轉化成無約束優化問題，進而借助無約束優化問題的最優性條件給出了等式約束最優化問題的最優性必要條件.但是由于不等式約束優化問題最優性條件的證明需要引入更多的符號與概念，因此國內常用的高等數學教材一般不對該問題進行研究.一般的最優化教材往往按照下面的思路研究該問題：為了給出不等式約束最優化問題的最優性條件，首先，引入3類向量集合，即可行方向集合、線性化錐和下降方向集合；然后，給出前2個集合的等價條件，后2個交集是空集的等價代數形式，該等價形式即為最優化問題的最優性一階必要條件.由于線性化錐與下降方向集合的交集可以表示成一個線性系統，因此通過Farkas 引理，該交集是空集等價于一個對應的線性系統有解，而由線性系統有解可得到最優性條件的代數形式[8-10].

具體分析過程見圖1.

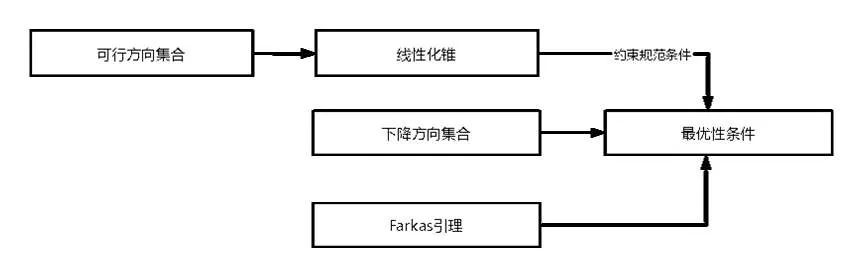
圖1 不等式約束最優化問題的最優性條件

考慮一個簡單的實例來說明不等式約束最優化問題的最優性條件分析過程.

例1考慮不等式約束優化問題

分析類似于數學分析課程所學的分析方法，為了求解該問題的最優解，需要找出可能的最優解，即挖掘最優解應該具有的性質.顯然，最優解應該滿足：（1）可行性；（2）在最優解處，沿著任意方向前進任意小的步長后，要么出了可行域，要么目標值上升，這說明在該點處不存在一個方向既是可行方向又是下降方向.由此分析得到最優解應該滿足條件

式中：I（x1,x2）為有效約束集合.于是必要條件可以松弛為

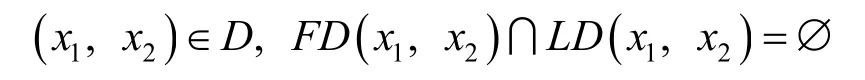
這樣處理產生了2個問題：（1）在什么條件下，FD（x1,x2）=LD（x1,x2）；（2）LD（x1,x2）的定義是一種隱式的形式，即只有知道了（x1,x2），才能求出I（x1,x2），這樣才能將LD（x1,x2）表示成不等式組.我們的目的就是求（x1,x2），這與求二次規劃的積極集時遇到的問題一樣，因此需要引入Farkas 引理，給出一個線性系統無解與另一個線性系統有界的結論，進而導出約束優化問題的一階必要條件.

由分析過程可以看出，與無約束最優化問題或等式約束最優化問題的最優性條件不同，不等式約束最優化問題的最優性條件需要引入集合、線性系統、Farkas 引理等一系列新的概念或結論.與同樣類型的問題相比，其分析過程有些繁瑣，沒有充分利用已經得到的結論.

課程教學內容的起承轉合對于學生建構一門課的內容體系起著非常重要的作用.本文針對不等式約束最優化問題的最優性條件設計一套全新的教學過程，其充分利用了等式約束最優化問題的最優性條件，避免了集合、線性系統、Farkas 引理等元素，遵循了“如無必要，勿增實體”的奧卡姆剃刀原理.

1 等式約束最優化問題的最優性條件

回顧等式約束最優化問題的最優性條件.考慮等式約束最優化問題

2 不等式約束最優化問題最優性條件的教學設計

基于等式約束最優化問題的最優性條件，給出不等式約束最優化問題最優性條件的教學設計.為了討論過程的簡潔，考慮只含不等式約束的最優化問題

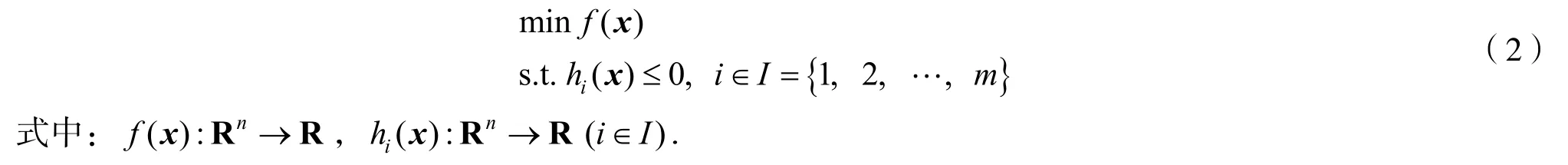
2.1 問題（1）與問題（2）的區別

問題（2）與問題（1）的區別只在于將等式約束換成了不等式約束.回顧在化線性規劃的一般形式為標準形式時，通過引入松弛變量可以將不等式約束轉化成等式約束.如對于約束x1+2x2≤ 1，引入松弛變量x3，得

為了保持約束的線性性，要求松弛變量x3非負.

2.2 形式轉化

受線性規劃標準化（3）的啟發，通過引入松弛變量，將問題（2）轉化成問題（1）的形式，即

2.3 初步結果

根據定理1 可得到問題（4）最優解滿足的一階必要條件.為此引入向量ei?Rm表示單位向量，其第i個元素為1，其余元素全為0.

2.4 乘子非負性的討論

與KKT 條件相比，式（7）對乘子的符號沒有施加限制，需要再考慮二階必要條件.

2.5 線性無關的討論

例2直接利用等式約束優化問題的最優性條件求解例1 中的不等式約束優化問題.

解引入松弛變量y1,y2，得

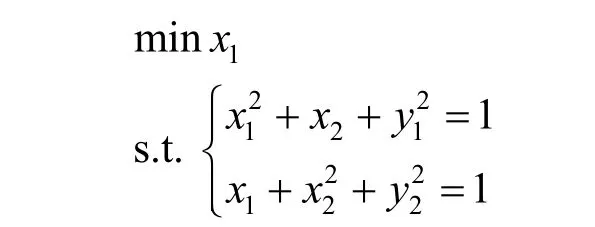
利用等式約束優化問題的必要條件得

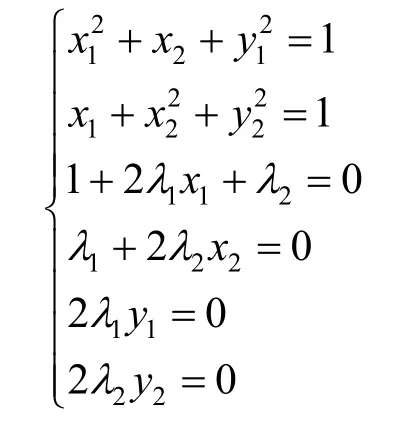
取d=（0,0,λ1,0），則d顯然滿足 2d1x1+d2+2d3y1=0,d1+2d2x2+2d4y2=0，于是由等式約束的二階必要條件可知，2λ13≥0，即λ1≥0.類似地，取d=（0,0,0,λ2），可得λ2≥0.將這些條件綜合到一起就得到了約束優化問題的K-T 條件.進而利用該K-T 條件求出可能的極值點，再結合最優性的二階必要與充分條件可以得到該問題的最優解.

比較例1 與例2 可以看出，直接利用等式約束優化問題的最優性條件來推導不等式約束優化問題的最優性條件是可行的，并且更便于學生理解這個知識點，同時便于構建起這一部分的知識邏輯體系.

3 結語

最優性條件是最優化方法課程的基礎而重要的內容.基于等式約束最優化問題的最優性條件，本文給出了不等式約束最優化問題一階最優性必要條件的一種新的教學設計思路.該思路沒有用到Farkas 引理，整個教學設計與已經學過的知識緊密結合，可以使學生從整體上更好地理解與掌握相關知識點，進而建構起最優化方法的結構體系.今后，將基于等式約束最優化問題的二階條件給出不等式約束最優化問題二階條件的教學設計.