水平定向擴孔器破巖切削力矩仿真研究

葛昭文 燕 翌 張 戈 李 云

（1.西安交通大學化學工程與技術(shù)學院；2.西北工業(yè)大學力學與土木建筑學院；3.中石化中原油建工程有限公司）

非開挖技術(shù)作為在地表不挖槽和地層結(jié)構(gòu)破壞極小的情況下對各種管線進行鋪設(shè)、修復(fù)和更換的施工技術(shù)，廣泛應(yīng)用于石油、天然氣工程中。 而水平定向擴孔器作為非開挖技術(shù)中的關(guān)鍵設(shè)備，由于進尺速度緩慢、擴孔切削力矩難以控制，在脆性巖土地質(zhì)中進行擴孔過程時，容易產(chǎn)生大塊巖屑孔內(nèi)堆積、破碎地質(zhì)鉆屑不易帶出等問題［1］。 因此，有必要針對不同巖質(zhì)，研究分析擴孔器切削力矩，減少對孔壁的擾動，同時提高鉆機擴孔速度和切削速度，提高擴孔的施工效率和成孔質(zhì)量。

目前擴孔器破巖過程中的切削力矩確定方式多為傳統(tǒng)理論計算求解法［2］，利用該方法確定切削力矩較為簡單，但因求解時未考慮巖體破碎的脆性特征，認為破巖過程中切削齒和巖體處于完全接觸的狀態(tài)［3］，力矩計算結(jié)果往往偏大，導(dǎo)致擴孔器功率過大，切削振動現(xiàn)象加劇，從而發(fā)生卡鉆等事故。 GOKTAN R M和YILMAZ N G通過實驗的方式研究了擴孔器切削巖土的特征，發(fā)現(xiàn)巖土的切削效率會隨著巖土脆性的增加而提高［4］；LI X F等用離散元方法研究了巖石脆性對巖石破碎和切削性能的影響。 研究認為在切割脆性較大的巖石時，切削力波動較大且切削效率比低脆性巖土要高［5］。 上述研究表明巖土切削力和巖土脆性密切相關(guān)。

筆者在考慮巖體脆性破碎特征的情況下，對擴孔器工作過程進行力學分析，建立擴孔器破巖的有限元模型，利用Abaqus軟件，對擴孔器切削過程進行數(shù)值仿真，以期獲得脆性巖土中擴孔器所需的最低切削力矩， 同時研究巖質(zhì)力學參數(shù)、擴孔器關(guān)鍵參數(shù)對切削力矩的影響，為實際工作擴孔器切削力矩的選取、結(jié)構(gòu)優(yōu)化、擴孔速度的提高提供理論依據(jù)。

1 擴孔器-巖土相互作用分析

擴孔器在工作時，由鉆機通過鉆桿提供擴孔器繞自身軸線轉(zhuǎn)動的扭矩和拉動擴孔器前進的拉力，通過擴孔器牙輪切削齒與巖體的相互作用實現(xiàn)對巖土的破碎，達到擴孔的目的。 圖1所示為擴孔器工作示意圖。

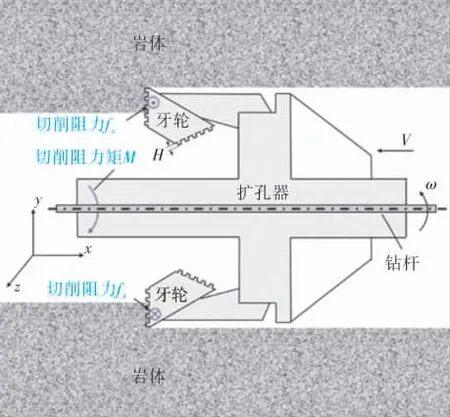
圖1 擴孔器工作示意圖

如圖1所示， 擴孔器工作時主要受到巖土的阻力矩M，切削刃上阻力矩（切削阻力矩）M表示刀刃對土體進行切削時土體阻力形成的力矩，為：

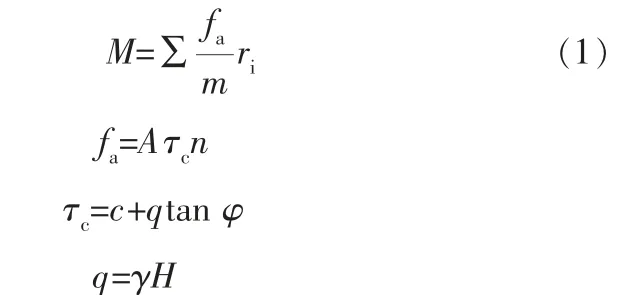
式中 A——等效接觸面積， 表征切削齒和巖體的接觸狀態(tài)， 可由擴孔器幾何結(jié)構(gòu)獲得；

c——巖土粘聚力；

fa——切削刃上所受的切削阻力；

H——巖土所在深度；

m——切削刃軸向組數(shù)；

n——切削刃軸向數(shù)目；

q——由巖土重力引起的圍壓；

ri——切削刃所在的擴孔器半徑；

γ——巖土重度；

τc——土體的切削破壞強度， 同時表示切削刃切削過程中從土體所受的最大臨界阻力， 可由摩爾-庫倫準則計算；

φ——巖土內(nèi)摩擦角。

2 擴孔器切削過程仿真

2.1 擴孔器切削仿真的基本假設(shè)

在擴孔器實際運行過程中，影響擴孔阻力矩的因素較多， 為了便于有限元仿真的研究，做出以下假設(shè)：

a. 鑒于擴孔器切削齒的強度和硬度遠高于巖體，將切削齒假設(shè)為剛體，且認為在鉆進過程中不發(fā)生磨損；

b. 假定巖體為連續(xù)的、均質(zhì)的、各向同性的材料，且不考慮巖體中原生裂紋和初始應(yīng)力場的存在；

c. 不考慮切削過程中漿液流場、溫度變化對巖體的影響；

d. 當巖體單元失效后即從巖體中移除，忽略其失效對后續(xù)擴孔的影響。

2.2 切削巖土本構(gòu)模型

在擴孔器破巖過程中，巖土受切削作用產(chǎn)生脆性破壞。 針對切削過程進行有限元模擬，需考慮受切削巖土的兩類本構(gòu)模型，即彈塑性本構(gòu)模型和損傷斷裂本構(gòu)模型。 前者描述擴孔器從初始接觸巖土到使之達到屈服前的應(yīng)力-應(yīng)變關(guān)系，后者描述巖土屈服后擴孔器繼續(xù)切削工作，使巖土損傷不斷累計直至斷裂失效的過程，分別對應(yīng)了圖2所示的OC階段和CE階段［6，7］。

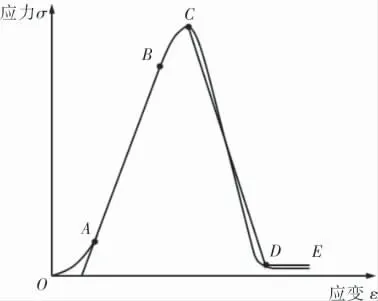
圖2 準脆性破碎巖土的應(yīng)力應(yīng)變曲線

對于彈塑性本構(gòu)，考慮巖土的特性，本研究采用了線性彈性模型和線性Drucker-Prager（D-P）塑性模型［8］，該模型改進了廣義的Von Mises屈服準則［9］，可以同時反映體積應(yīng)力、剪應(yīng)力和中間主應(yīng)力力對巖土強度的影響，且與損傷本構(gòu)模型能夠更好地相容。

線性彈性模型的表達式為：

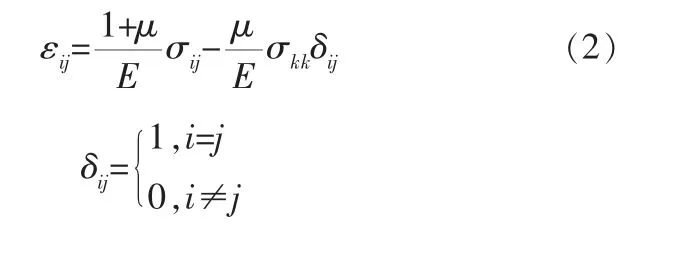
式中 E——彈性模量；

δij——一個單位張量；

μ——泊松比。

線性D-P模型的屈服軌跡如圖3a［8］所示，其函數(shù)為：

線性D-P模型的塑性勢面如圖3b［8］所示，其函數(shù)為：

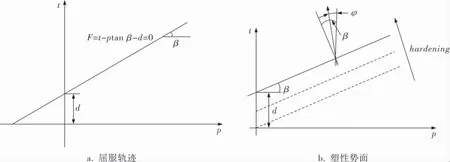
圖3 線性D-P模型的屈服軌跡和塑性勢面

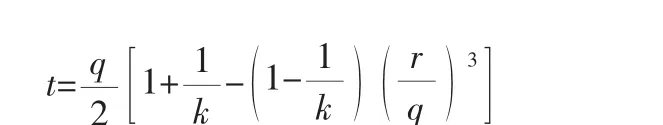
式中 d——材料的粘聚力；

k——三軸拉伸強度和壓縮強度之比；

p——等效壓應(yīng)力；

q——等效Mises應(yīng)力；

t——偏應(yīng)力；

β——屈服面在p-t應(yīng)力空間上的傾角，與摩擦角φ有關(guān)。

巖土損傷斷裂本構(gòu)模型可由應(yīng)力三軸度和失效位移兩個參數(shù)進行描述，較低的應(yīng)力三軸度和較大的失效位移將產(chǎn)生韌性斷裂模式，而較高的應(yīng)力三軸度和較小的失效位移產(chǎn)生脆性斷裂模式［10］。 當滿足下面的條件時，會發(fā)生損傷［11］：

基于巖土的線性彈性模型、D-P塑性模型和損傷模型，不同巖質(zhì)的材料參數(shù)設(shè)定見表1［12］。

表1 不同巖質(zhì)的材料參數(shù)

2.3 擴孔器有限元仿真的幾何模型及邊界條件

擴孔器切削過程采用有限元仿真，分析軟件為Abaqus 2020。 擴孔器工作時，進行切削作用的僅為牙輪上的切削齒，因此為了提高切削過程模擬的計算效率，僅建立切削齒和巖體的相互作用模型， 通過控制總接觸面積S0來實現(xiàn)不同結(jié)構(gòu)的牙輪和巖體的作用關(guān)系。

另外，實際切削過程為圓周運動，巖體在周向的力學運動模型是旋轉(zhuǎn)對稱的，因此，本研究建立圓周方向上的1/4旋轉(zhuǎn)對稱模型，這樣可在不影響求解精度的情況下減少計算量。

圖4為建立的切削齒和巖體接觸的有限元模型。 巖體和切削齒的三維實體單位類型均采用八節(jié)點六面體線性減縮積分單元（C3D8R），單元形狀使用六面體單元 （Hex）， 并采用結(jié)構(gòu)化網(wǎng)格（Structured），且對要發(fā)生切削破壞的巖體進行網(wǎng)格細化以提高計算精度。 網(wǎng)格無關(guān)性驗證結(jié)果如圖5所示， 從圖中可以看出隨著網(wǎng)格尺寸的減小和網(wǎng)格數(shù)量的增加，切削力矩計算結(jié)果呈現(xiàn)先不斷波動、后趨于穩(wěn)定的趨勢。 將網(wǎng)格尺寸細化至2.56 mm之后，誤差僅為2.3%，另外，考慮使切削齒和巖體之間具有更好的接觸關(guān)系，需要讓兩者初始接觸面上的節(jié)點一一對應(yīng)，取最終網(wǎng)格單元尺寸為2.5 mm。 依據(jù)潛江-韶關(guān)輸氣管道工程擴孔器工作參數(shù)［13］，切削過程參數(shù)設(shè)定為：摩擦系數(shù)0.4；切削齒轉(zhuǎn)動幅值-1.57 rad；切削等效線速度1.884 m/s。

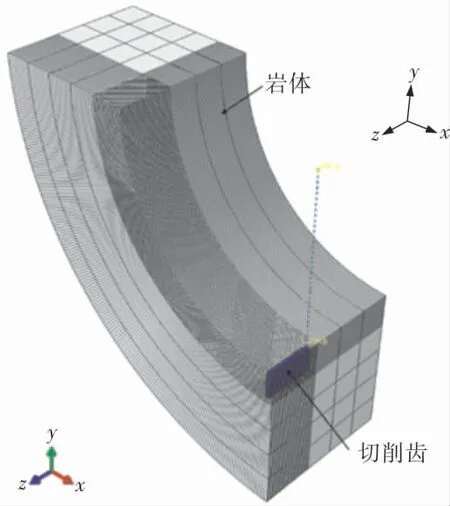
圖4 巖體-切削齒有限元模型

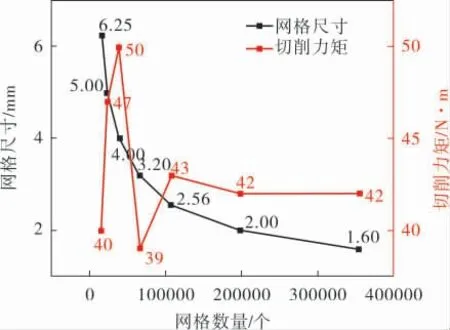
圖5 網(wǎng)格無關(guān)性驗證

3 切削過程仿真結(jié)果分析

利用Abaqus/Explicit對不同巖質(zhì)下各尺寸擴孔器切削巖土的過程進行動力學仿真，得到了巖體經(jīng)切削破碎后的Mises應(yīng)力分布結(jié)果，如圖6a所示。 為了更直觀體現(xiàn)巖體切削過程的脆性特征，將金屬經(jīng)切削后的Mises應(yīng)力分布進行對比分析，如圖6b所示。

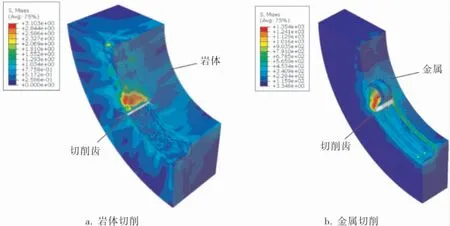
圖6 巖體和金屬切削過程Mises應(yīng)力分布

在切削過程中，巖體在切削齒運動的圓周方向上發(fā)生破壞，實現(xiàn)擴孔。 從切削后的巖體Mises應(yīng)力分布圖可以看出，巖體內(nèi)的應(yīng)力分布較為不均勻， 且整個計算巖體的應(yīng)力傳遞較為分散，這體現(xiàn)了巖土脆性破壞的特點；而金屬材料在切削過程中應(yīng)力傳遞現(xiàn)象不明顯，應(yīng)力大都集中在切削路徑上， 且金屬被切削后形成連續(xù)的切屑，屬于材料的韌性破壞。

圖7為炭質(zhì)灰?guī)r和金屬材料在切削過程中的切削阻力隨時間的變化曲線。

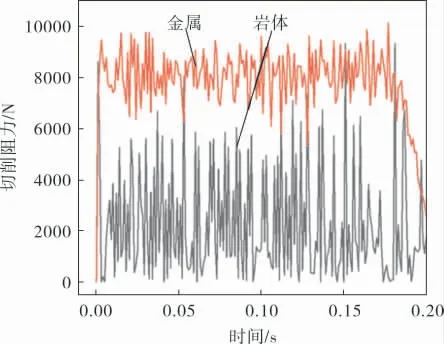
圖7 不同材料切削阻力隨時間變化關(guān)系

從圖7可以看出，巖土材料因脆性較高，切削阻力波動程度要高于金屬韌性材料，脆性巖土在動態(tài)加載下結(jié)構(gòu)的損傷破壞并不均勻，這是由應(yīng)力波傳遞［14］和材料失穩(wěn)［15］雙重物理機制決定的。因此切削刀具和巖土的接觸面積也應(yīng)處在劇烈變化之中，這導(dǎo)致巖土的破壞十分不穩(wěn)定，切削阻力呈現(xiàn)劇烈的周期波動現(xiàn)象。 相較而言，金屬材料切削過程中的切削阻力波動較炭質(zhì)灰?guī)r要低。 這是因為金屬材料材料屬于韌性材料，在動態(tài)切削過程中的力學穩(wěn)定性較高，切削齒和材料的接觸較為穩(wěn)定，未發(fā)生脆性破碎材料接觸面積劇烈變化的現(xiàn)象。

3.1 切削力矩結(jié)果分析

以潛江-韶關(guān)輸氣管道工程中不同尺寸擴孔器切削砂巖為例，將模擬所獲得的切削力矩和傳統(tǒng)方法計算所得切削力矩進行比較。 鑒于有限元計算考慮了巖土脆性破碎特征，而理論計算沒有考慮，因此可將切削力矩的有限元計算結(jié)果與傳統(tǒng)理論計算結(jié)果之比定義為擴孔器能耗比a。 a值越小，代表巖土脆性對切削過程能耗降低效果越明顯。 為了驗證有限元模擬切削力矩結(jié)果的準確性，可利用能耗比a進行驗證。 根據(jù)定義，結(jié)合巖土的脆性， 能耗比a也等于考慮脆性的切削比能和不考慮脆性的切削比能之比。 砂巖下切削力矩對比結(jié)果見表2。

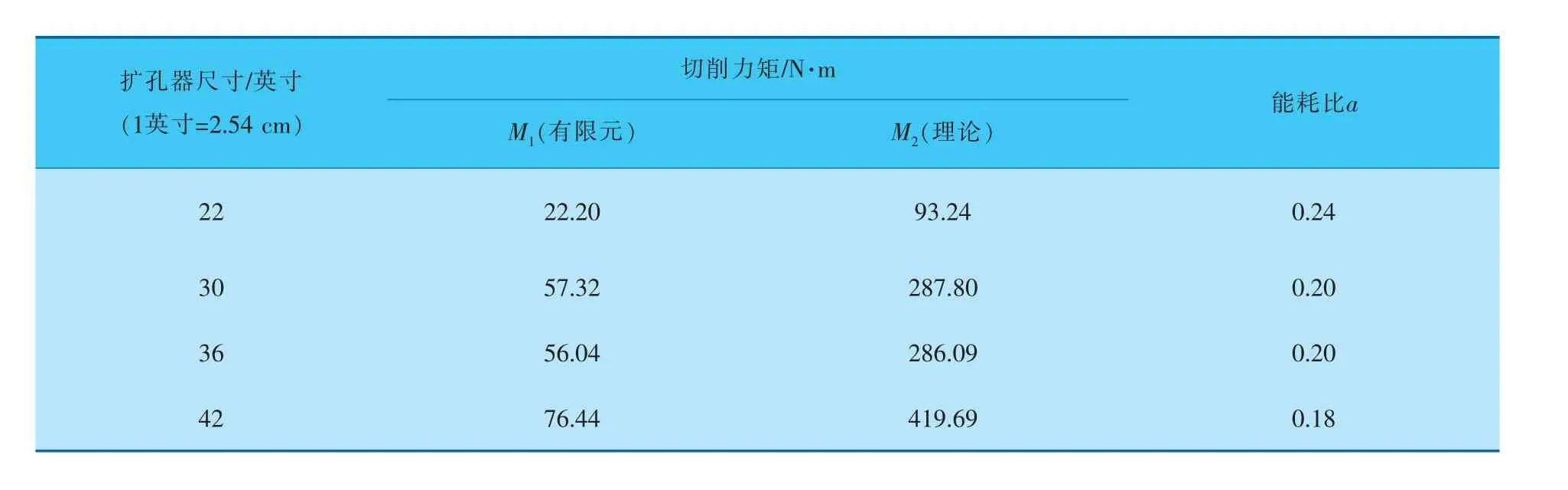
表2 砂巖下切削力矩對比

由表2可以看出， 有限元分析獲得的切削力矩比傳統(tǒng)理論計算值小很多。 這是由于理論計算未考慮巖土的脆性破壞特征，假設(shè)牙輪與巖體完全接觸，且?guī)r體強度分布均勻。 而事實上，由于巖土脆性高， 切削過程中和牙輪接觸面積不斷變化，且遠小于理論最大接觸面積，切削阻力波動較大。 因此擴孔器如果采用傳統(tǒng)理論計算的切削力矩，其切削效率則相對較低。

GOKTAN R M和YILMAZ N G通過實驗和數(shù)據(jù)擬合獲得了切削砂巖的比能和脆性指數(shù)的關(guān)系，其表達式為［4］：

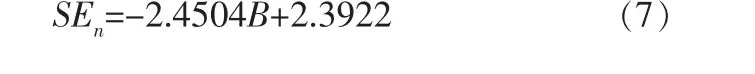
通過式（7）、（8）計算得到本研究所用砂巖的脆性指數(shù)B=0.75，比能SEn=0.55 MJ/（m3·MPa）；在不考慮巖土的脆性破碎特征的情況下，巖土脆性指數(shù)B=0，比能SEn=2.39 MJ/（m3·MPa）。 兩種情況分別對應(yīng)有限元計算和理論計算結(jié)果，將兩種情況下的切削比能進行比較，得到能耗比a=0.23。

對表2中不同尺寸擴孔器下的能耗比求平均，得到本研究中砂巖的平均能耗比為0.21，即通過研究發(fā)現(xiàn)，考慮巖土脆性后的能耗為不考慮巖土脆性情況下的21%， 與他人實驗數(shù)據(jù)擬合函數(shù)的計算結(jié)果之間的誤差為8.7%，可以驗證本研究有限元切削力矩模擬結(jié)果的可靠性。

3.2 擴孔器結(jié)構(gòu)參數(shù)對切削力矩影響分析

進一步，通過仿真還可探究結(jié)構(gòu)對切削力矩的影響，提出優(yōu)化方案，達到在保證擴孔效率的前提下，降低切削力矩的目的。

3.2.1 牙輪傾角對切削力矩的影響

在不同的擴孔級別下，通常需要設(shè)定擴孔器牙輪傾角，以適應(yīng)對應(yīng)級別下的擴孔需求，以潛江-韶關(guān)輸氣管道工程3級擴孔器結(jié)構(gòu)為基準，分析特定工況下不同牙輪傾角對擴孔器切削力矩產(chǎn)生的影響。 考慮牙輪的安裝性，牙輪最低傾角為8°，最高傾角為56°。圖8為不同牙輪傾角下的擴孔器切削力矩仿真結(jié)果。

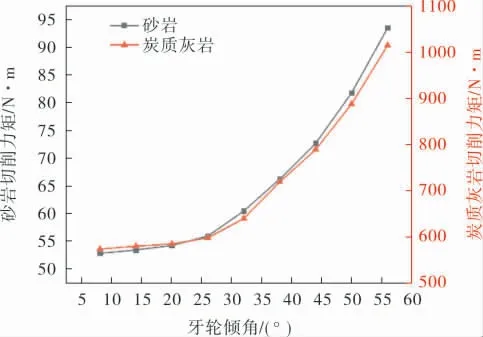
圖8 不同牙輪傾角下的切削力矩

由圖8可知，隨著牙輪傾角變大，擴孔器所需切削力矩呈上升趨勢，由于炭質(zhì)灰?guī)r的強度高于砂巖的，因此切削灰?guī)r所需力矩大于砂巖，但兩者的整體變化趨勢大致相同。 擴孔器切削力矩的變化趨勢在不同牙輪傾角增長區(qū)間內(nèi)呈現(xiàn)不同的規(guī)律，傾角為8°至25°時，擴孔器切削力矩增長趨勢較為緩慢；傾角為25°至45°時，切削力矩隨傾角增大的趨勢開始逐漸變快；傾角為45°至56°時，切削力矩的增長態(tài)勢明顯，在牙輪傾角從8°變?yōu)?6°的過程中，擴孔器切削力矩的增長率處于上升狀態(tài)，對傾角變大的敏感度越來越高。 這是由于在工況不變時，被切削巖體在垂直于擴孔方向上的高度是一定的，牙輪傾斜角度越大，和巖體的接觸面積越廣，切削所需力矩值也就越高，導(dǎo)致擴孔器切削效率降低。 另外，牙輪和巖體的接觸面積和切削角度呈倒余弦函數(shù)關(guān)系，所以在牙輪傾角變化區(qū)間內(nèi)，切削力矩關(guān)于傾角的變化率越來越高。 牙輪傾角的增大一方面會使牙輪的安裝難度降低，提高安裝工藝性；另一方面又會增大切削力矩，降低切削效率，所以工程中可取切削力矩增長趨勢緩慢的區(qū)間中的最大25°傾角作為最優(yōu)傾角，兼顧切削力矩和牙輪安裝難度兩種因數(shù)。

3.2.2 切削齒齒深對切削力矩的影響

切削齒作為擴孔過程中直接和巖土發(fā)生相互作用的結(jié)構(gòu)，其大小、形狀的變化會對孔內(nèi)巖屑堆積和擴孔器工藝產(chǎn)生較大影響。 分析了牙輪切削齒齒深變化對擴孔器切削力矩的影響， 圖9為不同牙輪切削齒齒深下的擴孔器切削力矩變化情況。由圖9可知，牙輪齒深越深，所需切削力矩越大， 且切削力矩隨齒深變大， 總體呈線性增長趨勢。 齒深越深， 牙輪所能切削的巖體深度也越深， 因此所需切削力矩的值隨之增高，擴孔器的擴孔速度也會提高。 但是齒深的增大也會給牙輪切削齒和擴孔器鉆桿帶來較大的負荷， 即增大切削齒的應(yīng)力和鉆桿所受扭矩；另外， 切削齒在實際擴孔工作中會不斷磨損，齒深逐漸減小， 會降低切削力矩， 但也影響切削效率和擴孔質(zhì)量。

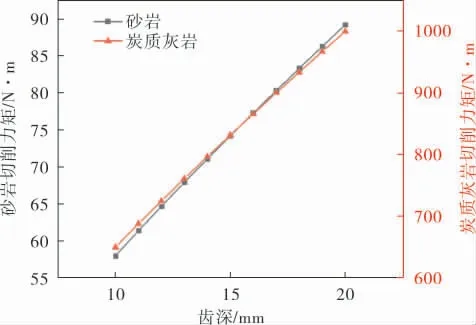
圖9 不同齒深下的切削力矩

4 結(jié)論

4.1 基于砂巖和炭質(zhì)灰?guī)r兩種巖質(zhì)，建立了擴孔器和巖土之間相互接觸的有限元模型， 對擴孔器切削巖土進行仿真， 發(fā)現(xiàn)受脆性影響，巖土材料在切削過程中的切削阻力波動程度遠高于金屬韌性材料； 計算得到了考慮巖土脆性破碎特征下的擴孔器切削力矩。 通過和理論計算比較， 發(fā)現(xiàn)巖土脆性會降低切削力矩和能耗，提高切削效率。 將本研究的平均能耗比和通過他人實驗擬合函數(shù)計算出的能耗比進行比較，誤差在可接受范圍內(nèi)， 驗證了切削仿真的可靠性。

4.2 通過分析牙輪傾角對切削力矩的影響，發(fā)現(xiàn)在牙輪傾角從8°增為56°的過程中，擴孔器所需切削力矩呈上升趨勢， 且力矩的增長率不斷提高，切削效率也不斷降低，但小牙輪傾角會使牙輪的安裝難度增加， 綜合安裝和切削力矩的問題，可在切削力矩增長趨勢緩慢的區(qū)間中取最大25°傾角為最優(yōu)傾角， 在保證切削力矩較小的前提下，降低牙輪安裝難度，達到擴孔器結(jié)構(gòu)和工藝上的優(yōu)化平衡。

4.3 淺切削齒齒深可帶來低切削力矩優(yōu)勢，但是切削速度較低，且牙輪耐磨損性能較差，影響成孔質(zhì)量；加深牙輪切削齒齒深可加深切削巖土深度，提高切削速度，但也會增大擴孔器所需切削力矩，給切削齒和鉆桿帶來更大的負荷，增大切削齒的應(yīng)力和鉆桿所受扭矩，在擴孔器設(shè)計時需綜合考慮此結(jié)構(gòu)和工藝上的因數(shù)。