基于固定界面法的旋轉裂紋葉片動力學特性分析

陳雪蓮，曾勁，馬輝

（1.遼寧省交通高等專科學校信息工程系，沈陽 110122；2.西南交通大學力學與航空航天學院，成都 611756；3.東北大學機械工程與自動化學院，4.航空動力裝備振動及控制教育部重點試驗室：沈陽 110819）

0 引言

旋轉葉片常承受著離心載荷、氣動載荷等復雜交變載荷的聯合作用，極易導致葉片疲勞裂紋的萌發[1-3]。開展葉片裂紋的早期損傷監測，及時發現并更換故障葉片，對于減少停機時間和維護成本，避免災難性事故的發生具有重要意義[4]。

目前，對故障葉片多采用基于振動的分析方法進行診斷[5]。Liu等[6]采用自編裂紋六面體單元建立了裂紋直板葉片的動力學模型，并與基于軟件開發的采用接觸單元建立的裂紋葉片模型進行了振動特性的對比驗證；Cheng等[7]采用p型有限元方法推導了旋轉錐型裂紋葉片的動力學方程，并與采用傳統有限元方法建立的模型進行了對比，從而驗證了其模型的有效性；李宏坤等[8]基于構造的WSG隨機共振模型提取了離心式壓縮機中含裂紋葉片的故障特征頻率；Shukla等[9]和Fu等[10]研究了不同裂紋尺寸對葉片前3階模態的影響，并進行了試驗驗證；Saito等[11-12]、D'souza等[13]采用混合模態綜合法研究了邊緣穿透裂紋對旋轉葉片頻率特性的影響以及葉尖處承受諧波載荷作用下系統的振動響應；Wang等[14-16]采用混合界面模態綜合法對含裂紋葉片的離心式壓縮機進行了自由度縮減，在此基礎上研究了單點集中諧波載荷作用下系統的振動響應。以上有關裂紋葉片的研究多簡化為結構較簡單的梁/板類模型，并在此基礎上開展裂紋對葉片動力特性的定性分析，而涉及到結構更為復雜的裂紋葉片模型，如變厚度扭形裂紋葉片，則較多地從試驗角度進行測試和分析。此外，很多學者盡管也采用模態綜合法對裂紋葉片進行了降維處理，但多分析減縮的旋轉態裂紋葉片模型（降維模型）承受非面載作用時的振動響應，而實際上葉片在旋轉態下往往受到氣動面載荷的作用。

本文主要在前人研究的基礎上，基于ANSYS分析軟件，采用固定界面模態綜合法對旋轉態下的變厚度扭形裂紋葉片進行了自由度縮減，并考慮裂紋面處的接觸特性以及旋轉引入的離心剛化效應分析了裂紋葉片在承受氣動面載荷作用下的振動響應，并與未減縮模型進行了精度和效率的對比。

1 裂紋葉片模型

1.1 裂紋葉片的有限元模型

裂紋葉片模型如圖1所示。圖1（a）為裂紋葉片在進行降維處理時所劃分的3個超單元區塊（超單元1、2、3）。此外，對于主節點的選取，除保留超單元的界面節點外（界面2和3上的所有節點），還保留了界面1處所有節點（其目的是為了對葉根施加固支約束）、葉尖處邊線1和2上所有節點（主要控制葉片模型的1階扭轉特性）以及區域Ⅰ和Ⅱ上的所有節點（主要控制葉片模型的彎曲特性）作為主節點（圖1（a））。

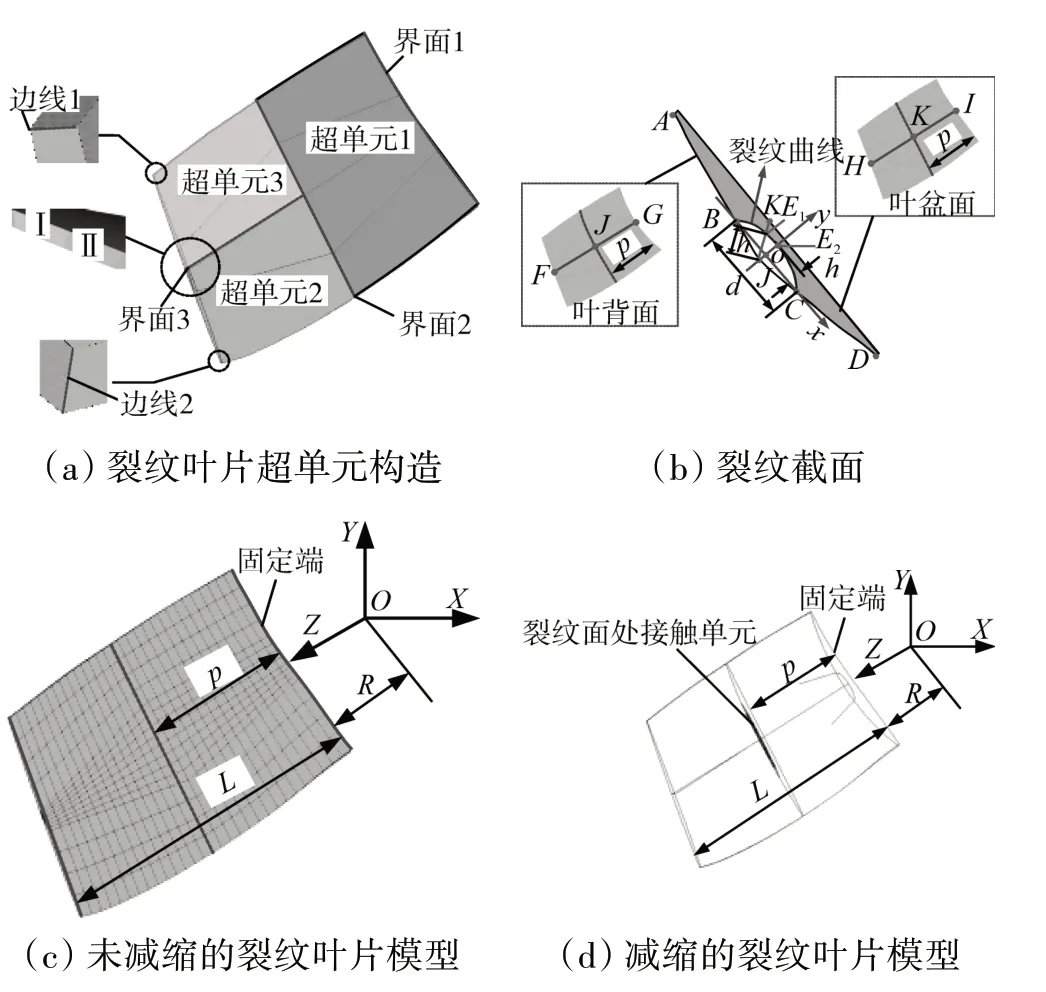
圖1 裂紋葉片模型

圖1（b）為葉片裂紋的截面（對應圖1（a）中界面2處的剖視圖），圖中裂紋曲線采用半橢圓方程來描述，其中，弧JC的長度為弧JCD的長度與無量綱裂紋深度d的乘積；弧JB的長度為弧JBA的長度與無量綱裂紋深度d的乘積；線段JE1的長度為線段JK的長度與無量綱裂紋深度h的乘積。此外，關于葉片裂紋建模還有如下說明：式（1）局部坐標系oxy的建立以及坐標原點o的選取；式（2）J和K點的確定。對于式（1），o為線段BC的中點，且■→■■oC向為x軸正向，y軸正向可通過將x軸逆時針旋轉90°得到。對于式（2），J點為葉背面上連接F和G點的最短弧線FG與裂紋截面的交點（F和G點分別對應葉背面上葉尖和葉根處的曲線中點），而K點為葉盆面上連接H和I點的最短弧線HI與裂紋截面的交點（H和I點分別對應葉盆面上葉尖和葉根處的曲線中點）。

圖1（c）、（d）分別對應裂紋葉片的未減縮模型和減縮模型。圖中p為葉片裂紋位置（取p=0.5L），R為葉片旋轉半徑（R=219.02 mm），L為葉片長度（L=88.87 mm）。

葉片的材料參數設置如下：楊氏模量E=125 GPa，泊松比υ=0.3，密度ρ=4370 kg/m3。裂紋葉片采用全六面體網格進行劃分，分網單元采用Solid185。此外，為了模擬葉片裂紋的呼吸效應，采用接觸單元來進行模擬，其中接觸的設置如下：靠近葉片固定端的裂紋面采用Targe170單元來進行網格劃分，而遠離葉片固定端的裂紋面則采用Conta174單元來進行網格劃分。

1.2 基于固定界面法的裂紋葉片降維理論

對于得到的離散裂紋葉片有限元模型，其動力學方程為

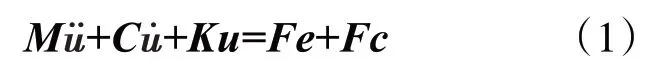
將式（1）中的矩陣方程按主自由度（與保留的主節點相對應的自由度）、從自由度（非主節點對應的自由度）作如下歸類整理

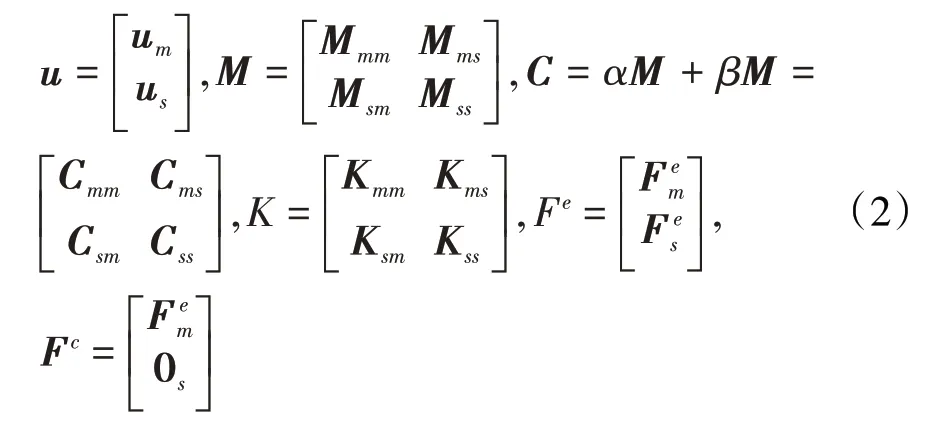
式中：M、C、K、Fe和Fc分別為裂紋葉片的質量矩陣、阻尼矩陣、剛度矩陣、外激振力向量和非線性接觸力向量；u¨、u˙和u分別為葉片的節點加速度、節點速度和節點位移向量；α和β為瑞利阻尼系數，本文中取α=31.69，β=2.91×10-6；下標“m“表示主自由度，“s”表示從自由度。

基于固定界面法[17-18]，對式（1）中的節點位移作如下坐標變換

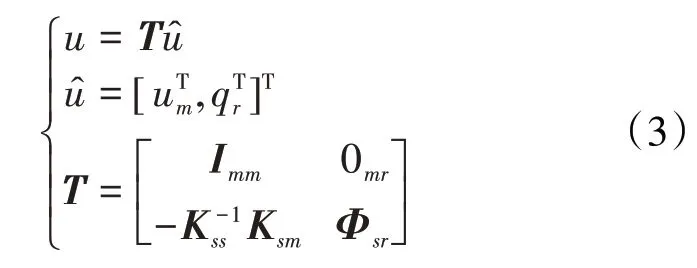
式中：T為坐標變換矩陣；I為單位矩陣；Φ為在主節點固定下得到的與保留模態截斷階數r（r＜＜s）相對應的特征向量；q為廣義模態坐標向量。

將式（3）代入式（1）同時在式（1）的左右兩端同時左乘TT，得到維數為（m+r）階的葉片動力學方程

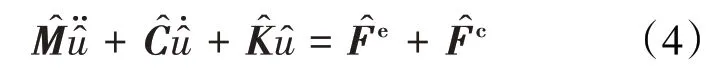
本文分析中取模態截斷數r=1。

2 裂紋葉片的動力學特性分析

針對得到的減縮裂紋葉片模型，分析其前3階動頻特性以及特定轉速下，減縮模型承受氣動面載荷作用時的振動響應，并與未減縮模型進行對比驗證。

2.1 裂紋葉片的固有特性分析

開裂紋葉片前3階固有頻率隨轉速的變化規律如圖2（a）～（c）所示。對于 給 定轉速區間n∈[0，10000]r/min，減縮裂紋葉片模型和未減縮裂紋葉片模型前2階固有頻率吻合較好（誤差＜0.5%），第3階動頻誤差稍大（最大誤差約為1.4%），如圖2（d）所示。轉速n=10000 r/min時減縮模型和未減縮模型的前3階模態如圖3所示，結果吻合較好。

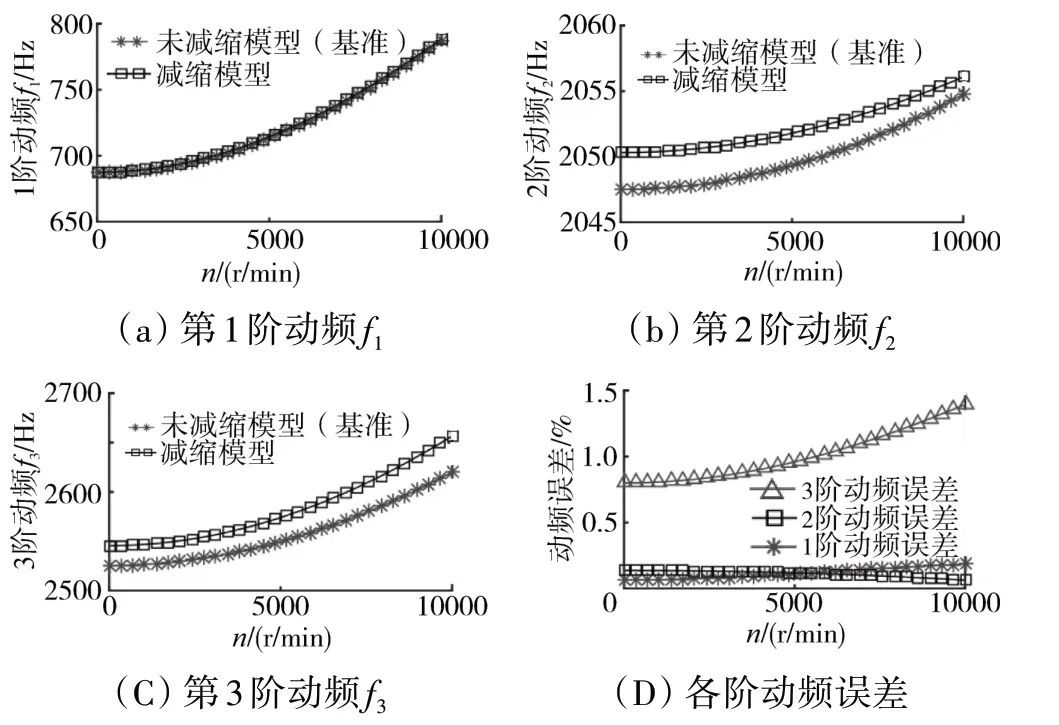
圖2 開裂紋葉片前3階動頻對比

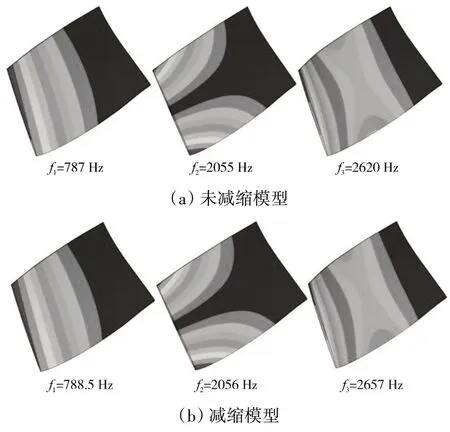
圖3 開裂紋葉片前3階振型對比（n=10000 r/min）

2.2 裂紋葉片的瞬態響應分析

動頻分析表明，減縮模型與未減縮模型的誤差較大值主要存在于轉速區間端點值n=0、10000 r/min，同時，為了考慮與轉速相關的氣動載荷作用，選取轉速n=2000、10000 r/min時，裂紋葉片葉盆面（圖1（b））承受氣動載荷P（t）=F0sin（2πkfrt）/Ab作用下的振動響應。F0為作用于葉盆面上的總力，Ab為葉盆面面積，k為轉子葉片前排的定子葉片數，fr為轉頻（fr=n/60 Hz），t為求解時間。本文研究中取F0=50 N，Ab=5311.8 mm2，k=10，t=10/fr。本文在仿真分析中取時間積分步長Δt=1/（60kfr）。

在n=2000、10000 r/min時減縮模型和未減縮模型的求解時間對比見表1，減縮模型的求解時間比未減縮模型的短，且減縮模型在低轉速條件下效率提高顯著。在n=2000、10000 r/min時裂紋葉片承受氣動載荷作用下X向和Y向的振動響應如圖4、5所示（Z向振動響應遠小于X向和Y向，故在本文中不考慮）。從圖4中可見，在n=2000 r/min時減縮模型和未減縮模型的振動響應和頻譜成分吻合較好，且有明顯的2fe成分出現，這主要是由于葉片裂紋呼吸導致的非線性效應。從圖5中可見，高頻激勵下減縮模型和未減縮模型響應差別稍大（相對于低頻激勵），但頻率成分基本吻合。造成這種誤差的原因主要是由于激勵頻率fe選擇過高，從而與固定界面模態綜合法在理論推導過程中要求激勵頻率fe應遠小于部件（即圖1（a）中的超單元1、2、3）的1階固有頻率[18]相矛盾所致。

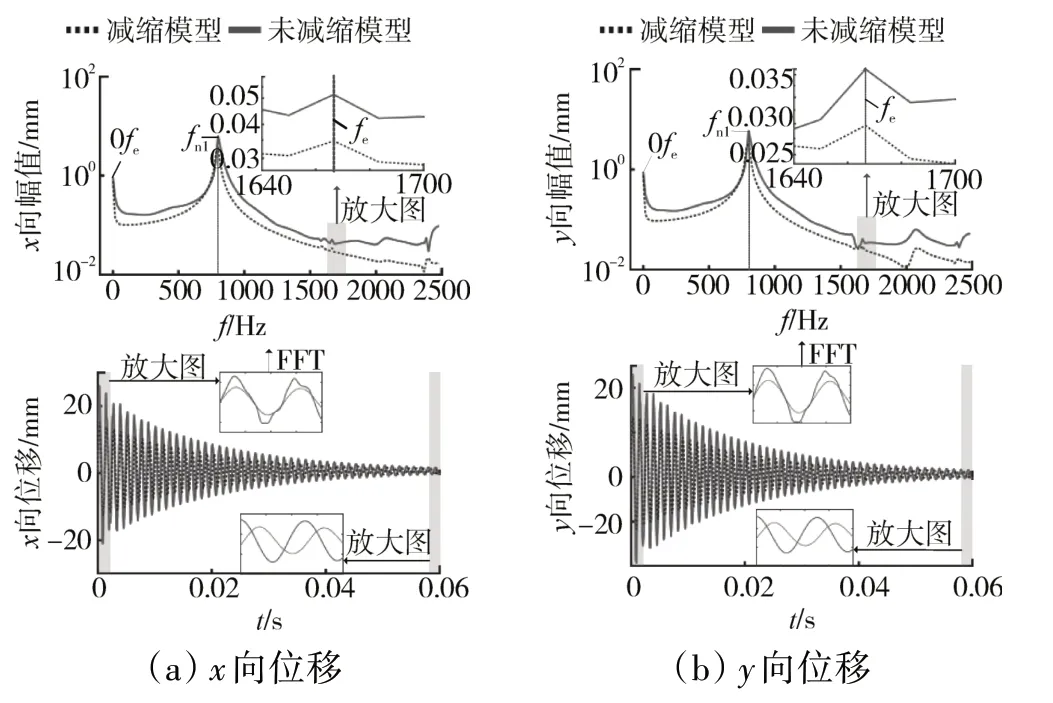
圖5 減縮模型和未減縮模型的振動響應對比（n=10000 r/min）

表1 減縮模型和未減縮模型求解時間對比

裂紋面上的接觸壓力時程曲線如圖6所示。圖6（a）中裂紋面上的接觸壓力時程曲線也證明了圖4中表現出的裂紋的呼吸效應；圖6（b）則表明n=10000 r/min時裂紋面上的接觸壓力逐漸衰減至0，即出現了不呼吸的情況。此外，圖4～6還表明高頻激勵下系統達到穩定所需時間較長。在n=2000、10000 r/min時與圖4、5標注的頻率成分相對應的減縮模型和未減縮模型的幅值對比見表2。

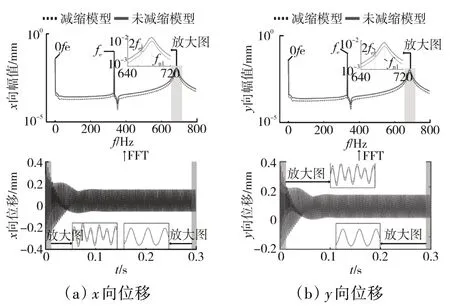
圖4 減縮模型和未減縮模型的振動響應對比（n=2000 r/min）

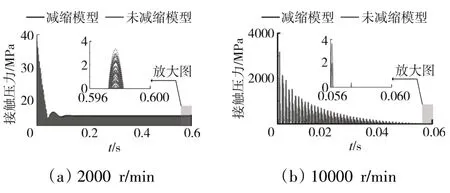
圖6 裂紋面上的接觸壓力時程曲線

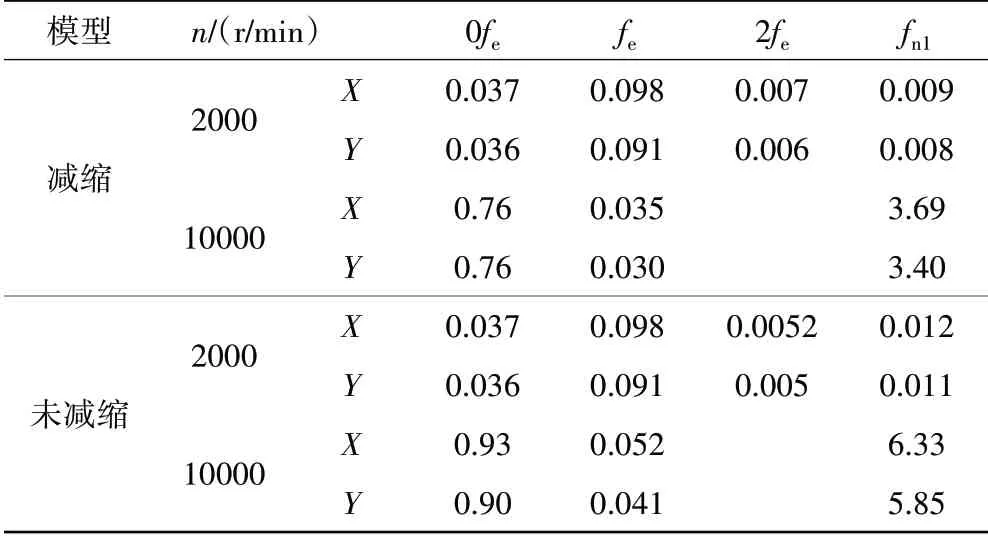
表2 減縮模型和未減縮模型的幅值對比 mm

3 結論

（1）葉片裂紋的呼吸特性取決于離心載荷和氣動載荷的聯合作用，且在低轉速下氣動載荷占主導，在高轉速下則離心載荷占主導。

（2）在低轉速下減縮模型的求解時間比未減縮模型的縮短約37.35%，而在高轉速下求解時間縮短約12.33%。造成這種差異的原因主要是由于在低轉速下裂紋呼吸效應導致的接觸迭代和未減縮模型自由度數眾多而導致耗時更長，而在高轉速下裂紋呼吸效應較弱甚至消失，因而計算時幾乎僅取決于模型的自由度數。換言之，在低轉速下減縮模型的求解效率比在高轉速下的偏高。

（3）減縮模型在低頻和高頻載荷激勵下的頻譜成分與未減縮模型的相同，且在低頻激勵下各頻率成分的幅值也幾乎相同，而在高頻載荷激勵下的幅值差別稍大。因此，應根據實際情況合理選擇激振頻率，并對其結果精確度作相應的驗證。