基于級聯卷積神經網絡的非笛卡爾磁共振重建

覃 芹，張 利，2，張達敏，蔡宇佳，冉文兵

（1 貴州大學 大數據與信息工程學院，貴陽 550025；2 貴州大學 省部共建公共大數據國家重點實驗室，貴陽 550025）

0 引言

磁共振成像（Magnetic Resonance Imaging，MRI）利用核磁共振原理進行圖像重建，具有無放射性損害、對比度高等特點，現已廣泛應用在醫學成像上，是臨床診斷中不可或缺的技術工具［1］。MRI 過程由數據采集過程和重建過程組成，需用到的數據采集方式有笛卡爾采樣和非笛卡爾采樣。其中，非笛卡爾采樣是加速磁共振成像的一種重要方法，能夠極大地減少數據采集時間。

傳統的非笛卡爾重建，主要有NUFFT（Non-Uniform Fast Fourier Transform）算法和網格化（Gridding）算法。Gridding 算法是1975年由Brouw［2］最先提出并應用在天文數據處理上，后經發展被廣泛應用在核磁共振成像和計算機層析等成像中。1993 年，Dutt 等人［3］全面研究了NDFT 問題的4 種格式，給出了快速算法使用插值公式將數據值從非均勻坐標點轉至均勻的坐標點處，并使用標準的傅里葉變換達到快速計算的目的，這是NUFFT首次被提出［3-4］，此后發展至nufftt 可由tfkbnufft 和torchnufft 實現。在實現上，網格化算法和nufft 算法都是卷積插值的過程，即利用合適的卷積函數與非笛卡爾采集到的磁共振數據進行卷積，將其轉換到均勻分布的笛卡爾網格上。該過程存在大量冗余的計算量，同時也由于卷積函數選擇的問題還存在較大誤差，冗余計算和誤差是導致非笛卡爾成像速度慢和質量差的主要原因。

近年來，不少學者將深度學習應用在欠采樣的MRI 重建領域中，與傳統的基于模型的方法有所不同，基于深度學習的方法運用數據驅動技術，只要網絡設計得當就可以通過大量數據訓練實現非笛卡爾重建。Schlemper 等人［5］提出了一個深度級聯神經網絡，并使用數據一致性模塊（Data Consistency，DC）來保障數據的保真度。隨后榮楚譽［6］在級聯網絡的基礎上，通過添加非均勻變換層，將級聯網絡推廣至非笛卡爾情況。2018 年，Zhu 等人［7］提出了一種基于流行逼近的自動轉換（Automated Transform by Mainfold Approximation，AUTOMAP）的成像方法，提出一種統一的圖像重建框架，該方法難以找到契合的流形估計，導致模型難以收斂，可能存在過擬合。

為了提高非笛卡爾磁共振重建質量，本文提出了一種深度神經網絡—級聯卷積神經網絡［8-9］，利用密度補償來糾正非笛卡爾k 采樣空間的不均勻加權，利用forward nufft 運算子和adjoint nufft 運算子交替實現測量空間和圖像空間的交替修正問題。其中，圖像空間由3 個卷積層和1 個卷積去噪自編碼器組成，本方法的測量空間能夠充分利用原始k空間數據，圖像空間利用卷積去噪自編碼器能夠專注于高頻信息的學習。

1 相關工作

磁共振是一項生物磁學核自旋成像技術，通過施加一個射頻電磁波來輻射被檢測物體，以此產生磁共振信號，該磁共振信號就是k空間數據。研究中將利用計算機來分析磁共振信號，進而得到磁共振圖像。因此對于磁共振成像主要分為2 個階段：數據采集階段和重建階段。其中，數據采集階段就是k空間數據的填充過程，重建階段是實現從頻率域數據到圖像的過程。

1.1 問題建模

數據采集階段由采集設備決定，在笛卡爾情況下，得到的完全采樣的k空間，將其IFFT 即可轉換為磁共振圖像，在非笛卡爾情況下，k空間數據不是規則分布，需要利用數據重采樣技術將其轉換到笛卡爾網格上后再使用IFFT 進行成像。完全采樣的k空間數據和磁共振圖像之間的關系由式（1）來描述：

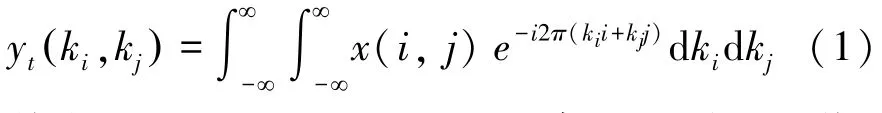
其中，x（i，j）是需要重建的目標圖像，yt(ki，kj) 是檢測到的MRI 信號，是頻率空間的表示。從式（1）可知，重建的圖像和檢測到的信號是一對傅里葉關系對。因此當MRI 信號已知時，圖像重建的過程可由式（2）來描述：

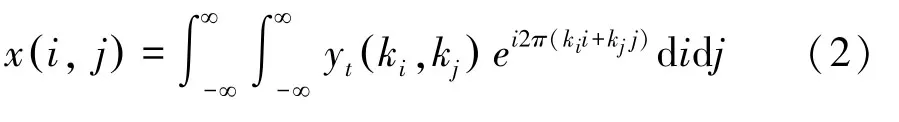
由于MRI 信號數據是復數形式，無法對其進行直接展示，所以在數據處理中一般是提取復數的幅值和相位數據，再從幅值和相位數據中重構出空間圖像。對于k空間數據，其中心部分對應于圖像輪廓，高頻部分對應圖像的細節部分，因此目前的圖像重建挑戰即是如何充分利用高頻信息得到高質量的圖像。

為了逼近更真實的磁共振重建場景，提高數據重建速度，提出非笛卡爾采樣條件，但是在該采樣條件下不能直接使用IFFT，需要利用數據重采樣將MRI 信號轉換到笛卡爾網格上。數據重采樣就是卷積插值的過程，其目的是將非笛卡爾采樣的MRI 信號卷積插值到均勻分布的網格上，該算法依賴于卷積函數的選取，其數學實現可由式（3）來描述：

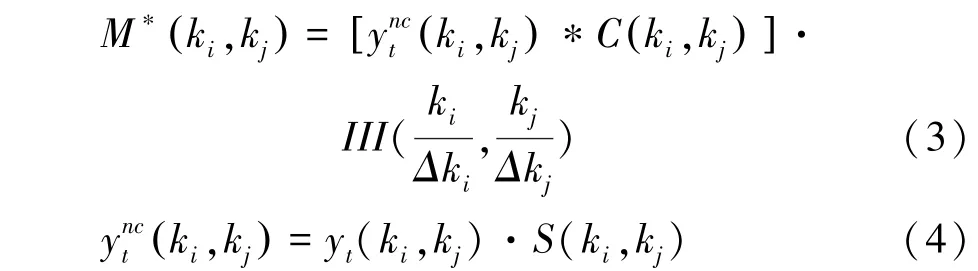
其中，M*表示卷積插值后的數據；(ki，kj) 是測量的非笛卡爾采樣數據；yt(ki，kj) 為笛卡爾采樣數據；S（ki，kj）為非笛卡爾采樣函數，本文中探討的非笛卡爾采樣是徑向采樣，因此S（ki，kj）為徑向采樣函數；C(ki，kj) 是網格卷積函數。

1.2 相關算法

非笛卡爾磁共振重建常用的算法有網格化（Gridding）和非均勻傅里葉變換（NUFFT）。一般情況下，Gridding 在射電天文成像中應用較為廣泛，NUFFT 算法則更多應用在磁共振圖像重建中。而NUFFT 算法主要分為2 個運算子。一個是前向（Forward）NUFFT 運算子，前向運算的目的是模擬成像過程中的非均勻頻率域數據。Forward NUFFT運算子的操作流程如圖1 所示。另一個是伴隨（Adjoint）NUFFT 運算子，這是一個成像過程，是將非均勻的數據變換到規則的網格上后、再進行成像。

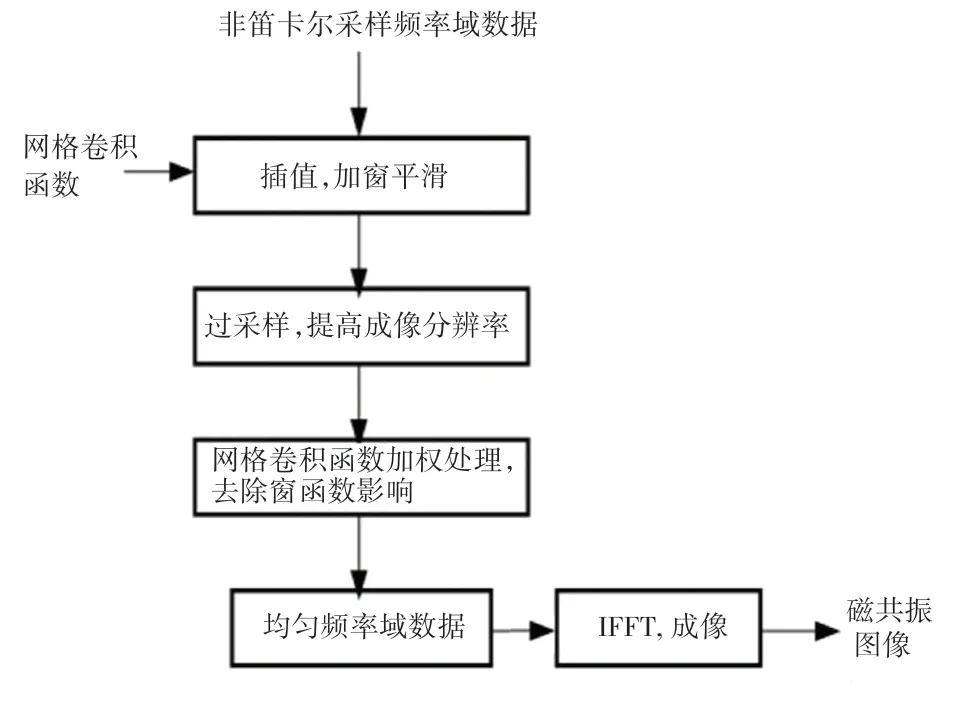
圖1 Forward NUFFT 運算子的操作流程Fig. 1 Operation flow of Forward NUFFT operator

根據迭代重建的原理，可將非笛卡爾欠采樣磁共振由式（7）描述：

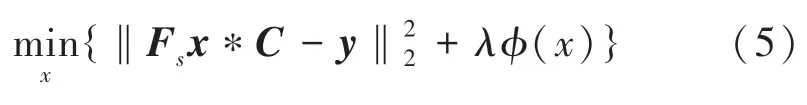
其中，x是待重建的目標圖像；y是原始k空間數據；Fs表示系統矩陣；Fsx是非笛卡爾欠采樣數據；C是網格卷積函數；‖Fsx*C -y‖為數據保真項；?（x）為正則化函數，對于傳統的方法來說，?（x）通常是x特定變換域的l0或l1泛式。

在選取網格卷積函數時，要滿足函數時域和頻域都具有良好集中性的要求，常用的網格卷積函數有Gaussian 函數、Kaiser-Bessel 函數和長波球函數PSWF 等。目前在磁共振非笛卡爾重建中，常用的是具有較好靈活性的Kaiser-Bessel 函數，研究時用到的時域表達式和頻域表達式分別見式（6）、式（7）：

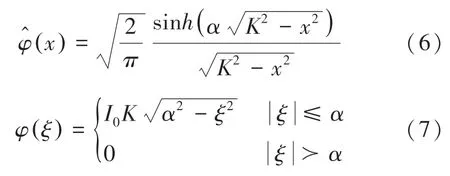
在執行插值運算時，要制定過采樣系數K和插值寬度W，每一個采樣點都有W2大小的窗口，從采樣點到插值窗口內的每個均勻點的距離決定插值權值。過采樣系數決定最終成像的分辨率。二者的選擇直接影響算法的速度，并且隨著過采樣系數K和插值寬度W的增大，算法的計算復雜度也會變大，由此即會帶來硬件計算問題，但這樣成像的誤差就越小，圖像質量也越高。綜上所述可知，隨著其值的增大，成像質量有所提高，但是成像速度較慢，因此在研究數據重采樣算法時需要平衡成像速度和成像質量，就要選擇合適的過采樣系數和插值寬度。

2 本文方法

非笛卡爾磁共振重建質量由重建算法決定，目前的重建算法存在冗余計算和計算誤差大的問題，導致重建結果較差，同時現有的神經網絡算法不能很好地提取高頻信息。為了實現高質量的非笛卡爾磁共振重建，本文提出一種基于密度補償的級聯卷積神經網絡。

2.1 方法理論

本文提出的非笛卡爾欠采樣磁共振圖像重建方法是一種迭代重建方法，該網絡是基于密度補償的級聯卷積神經網絡。方法的整體流程可做闡述如下：

（1）將采集的k空間數據進行非笛卡爾徑向欠采樣得到模型的輸入數據ync。

（2）將全采樣k空間數據進行逆傅里葉變換，得到真實的重建圖像xGT。

（3）將ync和xGT作為模型的訓練數據集對，經過網絡I次迭代后得到網絡重建結果xncpdnet。推得的數學模型公式可寫為：

其中，i為網絡當前迭代次數，i∈［1，I］；I為總的迭代次數，I ＝10；θi（i∈［1，I］）是每次迭代過程中的網絡參數。基于密度補償的神經網絡依賴于密度補償來糾正k空間的不均勻加權，利用非均勻變換層來連接測量空間和圖像空間，其中測量空間和圖像空間交替修正以補償更多的細節信息，實現高質量重建。這里給出網絡結構設計如圖2 所示。對此擬展開研究分述如下。

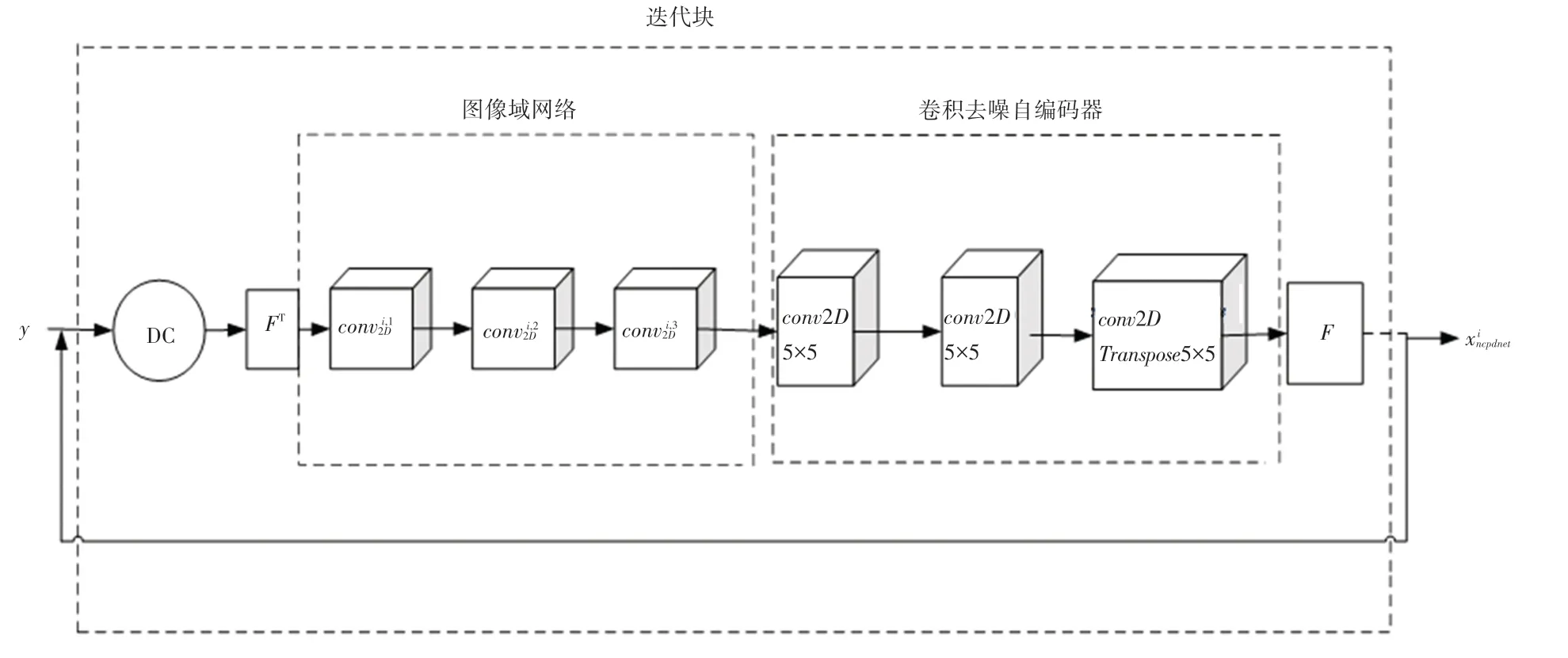
圖2 網絡結構圖Fig. 2 The structure diagram of the proposed network

（1）測量空間網絡。測量空間由數據一致性模塊（DC）組成，在每個步驟中引入原始測量數據，保證數據的一致性。DC 最早是由Schlemper 等人［5］應用在欠采樣的MRI 中。測量空間可由式（9）進行描述：

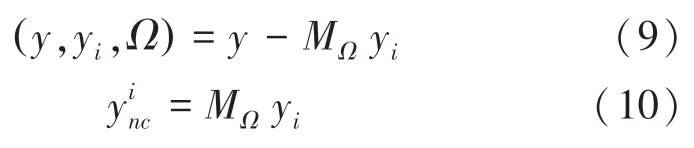
其中，y為原始全采樣k空間；yi為第i次迭代的全采樣k空間；Ω為采樣軌跡；MΩ為非笛卡爾徑向欠采樣。DC 模塊可以作為先驗知識來指導網絡的學習。

（2）圖像空間網絡。該部分網絡由3 個3×3conv2D組成，由于卷積是對實值進行操作，故而在輸入數據傳送至該模塊前將復數表現形式的k空間提取實部和虛部，再將其傳入新的通道數中。這就使得傳入圖像網絡空間數據的通道數比此前要多2 個通道數。該部分用于提取從測量空間到圖像空間映射的特征。

（3）卷積去噪自編碼器。自編碼器由編碼層和解碼層組成。編碼器旨在提取特征，解碼器是將特征通過與編碼層相反的網絡結構還原為原始數據。通過借助稀疏編碼的思想，使用稀疏的高階特征重新組合來重構自身，達到輸出與原始數據盡可能相似的目的。但是在實際圖像重建中存在重構誤差，因此在自編碼器的基礎上，可以添加噪聲來約束自編碼器重構。這可使得編碼器學習提取最重要的特征并學習輸入數據中更加魯棒的表示。

2.2 損失函數

磁共振重建是一個迭代重建的過程，從數學角度看是一個不斷最小化損失函數的過程。這一過程可以被描述為式（11）～式（13）：

3 實驗與結果分析

3.1 實驗數據

本文數據使用的是fastMRI 數據集（https：／／fastmri.med.nyu.edu／），該數據集是Facebook AI Research（FAIR）和NYU Langone Health 之間的合作研究項目，目的是研究使用AI 提高MRI 成像速度，并且從采樣不足的k空間數據中高效恢復出圖像，AI 進行MRI 圖像重建可以使MRI 更廣泛應用在醫療成像領域上，且符合更逼真的重建場景。fastMRI數據集包括2 種類型：膝蓋磁共振圖像和腦部磁共振圖像。數據集包括訓練集、驗證集以及masked 測試數據集。本實驗采用的是單線圈膝蓋數據集，圖像尺寸大小為320×320，平面分辨率為0.5 mm×0.5 mm，切片厚度為3 mm，切片之間無縫隙。訓練集總共有973 卷（973 個h5 文件，34 742 張圖片），驗證集共有199 卷（199 個h5 文件，135 張圖片）。

3.2 欠采樣模式

為了適應更真實的磁共振成像場景，提高數據的掃描速度，本文的欠采樣模式為非笛卡爾徑向欠采樣。圖3 顯示的是tfkbnufft 不同采樣模式下圖像重建的結果。圖3（a）～（c）中，左邊圖像是k-空間可視化，右邊圖像是在圖像域上的可視化。

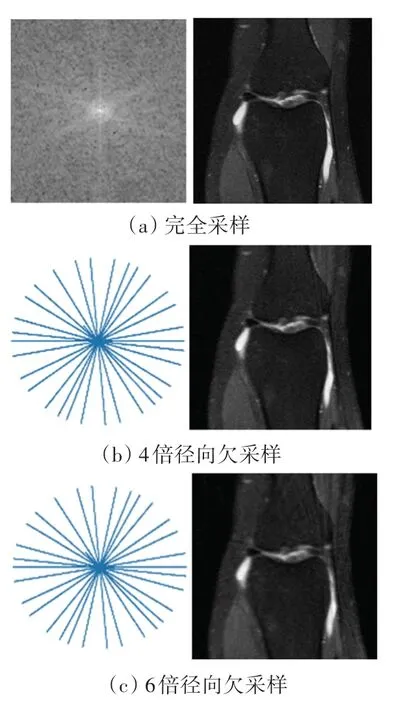
圖3 徑向欠采樣模式下k 空間與重建圖像的可視化Fig. 3 Visualization of k-space and reconstructed images in radial undersampling mode

3.3 評價指標

為了驗證本方法，采用每張圖像重建時間T和重建質量作為評價指標。重建質量指標為峰值信噪比和結構相似性。其中，峰值信噪比（PSNR）的定義是重建圖像與原始圖像之間對比質量的好壞，PSNR越高、表明重建質量越好；結構相似性（SSIM）的定義是比較重建圖像與原始圖像之間的相似性，主要從亮度、對比度和結構三個方面來進行比較，其值范圍為［0，1］，即值越接近1、就表示重建圖像越接近于原始圖像。

3.4 實驗環境與參數配置

本文基于密度補償的神經網絡模型是基于Tensorflow 2.7.0 版本實現的，顯卡型號為GPU RTX 3090 * 3，其中顯存大小為24 GB。CPU 型號為42核Intel（R）Xeon（R）Gold 6330 CPU ＠ 2.00 GHz，內存大小為180 GB。

網絡迭代次數I ＝10，測量空間網絡由數據一致塊構成，以殘差的方式不斷修正測量k空間和原始k空間數據之間的差距，圖像空間網絡由3 個卷積層組成，卷積大小都為3×3，由于卷積層只能處理實數，就需要k空間數據實部和虛部分別放入2 個通道，因此圖像網絡的輸入通道數為12，輸出通道數為10，核的初始化方式為glorot_uniform 方式。卷積去噪自編碼器用于提取高頻信息，該模塊由2 個卷積層和1 個反卷積層組成，其中卷積層卷積核大小為5×5。在網絡訓練時，batch_size設置為一卷數據集、即為一個h5 文件，損失函數為mse，優化器為Adamw，初始學習率為lr ＝10-5。訓練輪次為200 輪。

3.5 實驗結果

為了驗證方法在非笛卡爾欠采樣磁共振圖像重建中的有效性，以及卷積去噪自編碼器在高頻信息提取中的高效性，本文將比較3 種方法：

（1）傳統tfkbnufft 重建算法，是torchkbnufft 的進一步發展，在重建速度上優于torchkbnufft。

（2）基于密度補償的神經網絡（ncpdnet），通過在網絡中添加非均勻變換層重建非笛卡爾數據。

（3）基于密度補償的級聯卷積神經網絡，在ncpdnet 網絡的基礎上，為了提取高頻信息，使網絡具有更好的魯棒性，該網絡利用卷積去噪自編碼器學習更多細節信息，以下稱為ours。

運行后，4 倍非笛卡爾徑向欠采樣模式下重建質量和效率對比結果見表1，6 倍非笛卡爾徑向欠采樣模式下重建質量和效率對比結果見表2，4 倍欠采樣模式下不同迭代次數下ours 重建質量與效率對比結果見表3。圖4 展示的是在4 倍非笛卡爾欠采樣條件下，3 種方法的重建結果對比圖。

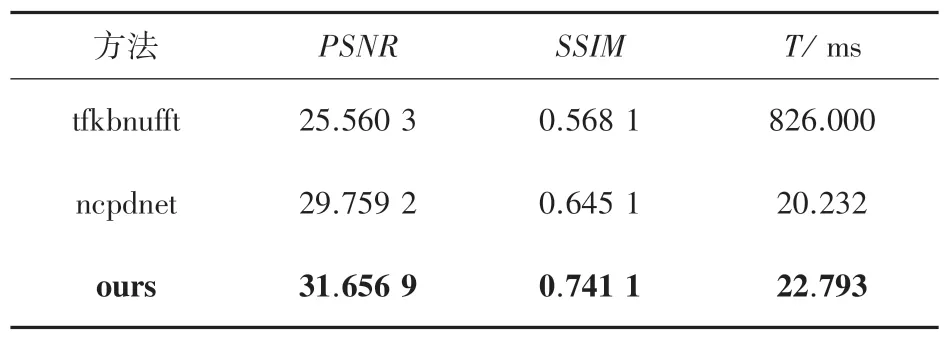
表1 4 倍非笛卡爾徑向欠采樣模式下重建質量和效率對比Tab.1 Comparison of reconstruction quality and efficiency in the 4x non-cartesian radial undersampling mode

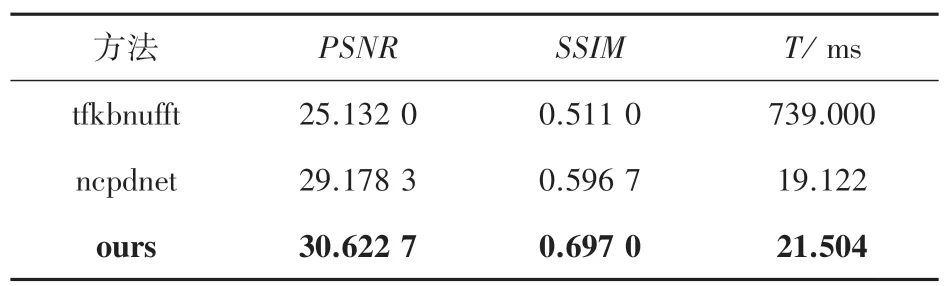
表2 6 倍非笛卡爾徑向欠采樣模式下重建質量和效率對比Tab.2 Comparison of reconstruction quality and efficiency in the 6x non-cartesian radial undersampling mode

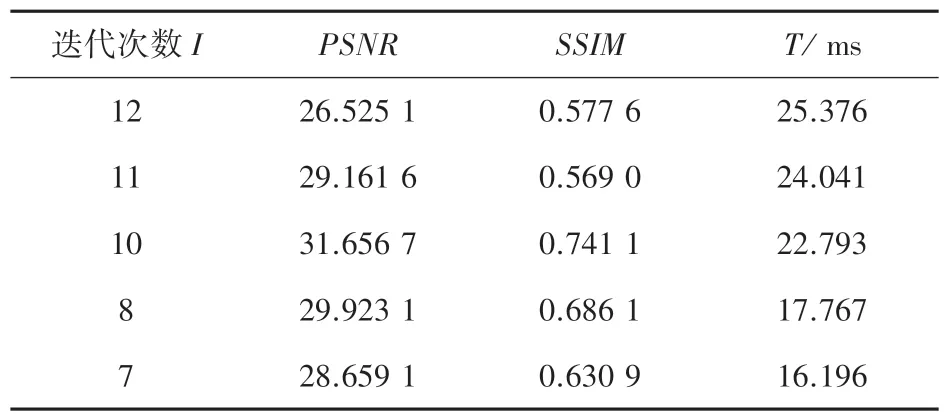
表3 4 倍欠采樣模式下不同迭代次數下ours 重建質量與效率對比Tab.3 Comparison of reconstruction quality and efficiency of ours under different iterations in 4x undersampling mode

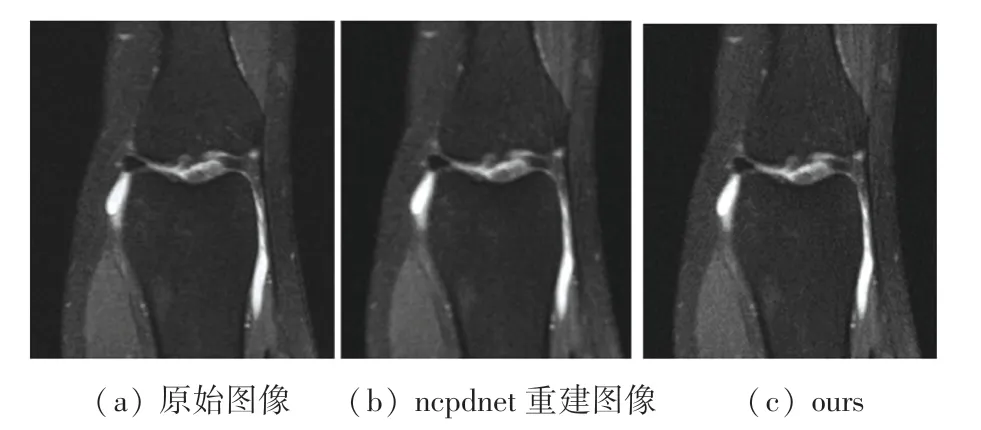
圖4 在4 倍欠采樣下3 種方法的重建結果圖Fig. 4 Reconstruction maps of the three methods under 4x undersampling mode

實驗結果表明，基于神經網絡的非笛卡爾欠采樣重建速度比傳統方法更快，主要是神經網絡的方法基于數據驅動，不需要進行插值運算；ours 相比ncpdnet 方法重建質量具有較大提升，主要是由于卷積去噪自編碼器能夠在密度補償展開網絡中發揮高頻信息提取作用，以重建出更多的圖像細節信息。同時，為了驗證I ＝10 是最佳迭代次數，對比了不同迭代次數下ours 重建性能。雖然本文提出的方法相比于ncpdnet 重建時間略長，這是由于模型參數量比ncpdnet 大造成的，不過這個細微的重建時間差別并不影響本文方法的性能。上述結果均是在測試集表現的結果。

4 結束語

本文提出了一種基于密度補償的級聯卷積神經網絡，該網絡用于非笛卡爾欠采樣磁共振圖像重建，在本方法中，將MRI 圖像重建過程視為從非笛卡爾數據中迭代重建的過程，為了提取重建過程中的高頻信息部分，將卷積去噪自編碼器用于該重建任務中。同時對比了不同加速因子欠采樣模式下重建質量和重建效率，通過實驗證明了本文方法具有更強的細節信息提取能力，在4 倍欠采樣和6 倍欠采樣模式下，本文的方法能夠有效提高重建圖像的峰值信噪比和結構相似性。本實驗建立在單線圈成像場景上，為了驗證卷積去噪自編碼器在密度補償神經網絡中提取高頻信息的能力，未來的工作可以將其應用到多線圈膝蓋以及腦部圖重建中。