基于自適應遺傳算法的隨機森林模型參數優化方法

蔡 明，孫 杰，楊維發，鮑 清，李培德

（1 湖北省氣象信息與技術保障中心，武漢 430074；2 中國氣象局武漢暴雨研究所暴雨監測預警湖北重點實驗室，武漢 430074）

0 引言

隨機森林回歸（Random Forest Regression）算法作為一種靈活且易于使用的機器學習算法［1-2］，其理論和方法已被作為一種替代一般線性模型（線性回歸、方差分析等）和廣義線性模型（邏輯斯蒂回歸、泊松回歸等）的方法，廣泛應用于工程應用和科學領域中復雜問題的解決上。國內外學者對隨機森林在回歸和分類問題中的應用進行了全面研究。在國外，Kulkarni 等人［3-4］為了提高分類正確率，將決策樹維度分為2 部分。Oshiro 等人［5］證明了在隨機森林性能達到最優時決策樹數目存在臨界值。Bernard 等人［6］研究了隨機森林強度與相關性的關系。在國內，袁遠等人［7］利用隨機森林算法對非線性數據特征的學習能力，優化ARIMA 模型預測殘差，最終達到提高回歸預測精度的目的。馬景義等人［8］綜合了Adaboost 算法和隨機森林算法的優勢，提出了擬自適應分類隨機森林算法。馮開平等人［9］將加權K 最近鄰法（KNN）與隨機森林算法結合應用于表情識別，簡化了計算復雜度的同時取得了不錯的識別率。

自適應遺傳算法是將生物進化論的自然選擇和遺傳機理應用于粒子濾波算法以克服其粒子多樣性退化不足的一種隨機化搜索方法［10-11］。其主要特點是按照優勢種群遺傳的原則將粒子適應度變化情況作為遺傳操作中交叉和變異概率變化的依據，通過對粒子的選擇、交叉和變異操作模擬生物界優勝劣汰、適者生存的過程，由于其直接對結構化的對象進行操作，故具有很好的全局尋優能力。但是由于遺傳操作中的交叉和變異概率是預先設定的，參數選取不當容易使算法陷入局部最優［12-15］。

基于以上研究論述，本文提出一種基于自適應遺傳算法的隨機森林回歸模型參數優化方法，使用Boston house price 數據集對經過該方法優化后隨機森林模型的回歸預測效果進行驗證。

1 相關算法介紹

1.1 隨機森林回歸算法

隨機森林回歸（Random Forest Regression，RFR）算法是一種基于決策樹（Decision Tree）的引入隨機特征選擇的Bagging 類集成算法，目前被廣泛應用于各類回歸問題。本文使用Boston house price 數據集對隨機森林回歸模型進行訓練和預測。隨機森林回歸模型的建立過程如下：

（1）從原始訓練集中使用bootstrap 方法隨機有放回采樣取出m個樣本，共進行n_tree次采樣。生成n_tree個訓練集。

（2）對n_tree個訓練集，分別獨立訓練n_tree個決策樹模型。

（3）對于單個決策樹模型，假設訓練樣本特征個數為n，選擇最好的特征進行切分。

（4）每棵樹都按照步驟（3）來切分下去，直到該節點的所有訓練樣例都屬于同一類。在決策樹的切分過程中不需要剪枝。

（5）將生成的多棵決策樹組成隨機森林，模型最終預測結果為隨機森林中多棵決策樹預測結果的均值。

決策樹的生長過程就是使用滿足劃分準則的特征不斷將數據集劃分為純度更高、不確定性更小的子集的過程。

在步驟（3）中，當訓練決策樹模型時需要考慮怎樣選擇切分特征、切分點以及怎樣衡量切分特征、切分點的好壞。針對切分特征和切分點的選擇，本文采用窮舉法，即遍歷每個特征和每個特征的所有取值，再從中找出最好的切分變量和切分點；針對于切分特征和切分點的好壞，一般以切分后節點的不純度來衡量，即各個子節點不純度的加權和G（xi，vij），其計算公式如下：

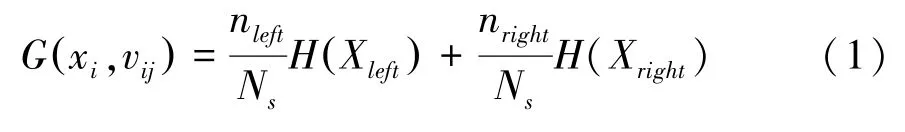
其中，xi為節點的某一個切分特征；vij為切分特征的一個切分值；nleft、nright、Ns分別為切分后左子節點訓練樣本個數、右子節點訓練樣本個數以及當前節點所有訓練樣本個數；Xleft、Xright分為左、右子節點的訓練樣本集合；H（X）為節點的不純度函數（impurity function），回歸模型一般采用均方誤差（Mean Square Error，MSE）或平均絕對誤差（Mean Absolute Error，MAE）作為不純度函數，本文則選用了MSE作為模型的不純度函數，其數學定義公式見式（2）：

其中，Xs為當前節點訓練樣本集合；ns為當前節點訓練樣本數目；為當前節點樣本目標特征的均值。

將式（2）帶入式（1）后，對于任意切分點可以得到：

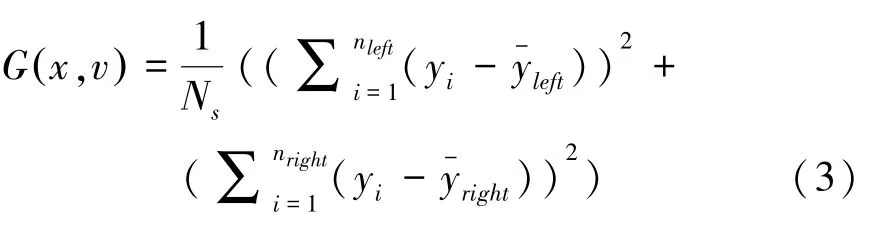
1.2 自適應遺傳算法

以往的遺傳算法常使用恒定不變的概率對粒子進行交叉和變異等遺傳操作，這樣會導致粒子群中適應度較大的優勢粒子容易被丟棄掉，同時新的優勢粒子也不容易產生，致使算法一旦陷入局部最優，就很難跳出。

針對這一問題，提出一種基于生物遺傳進化思想的自適應遺傳算法（AGA）。算法中，高適應度的優勢個體以較高概率進行交叉操作，這樣可以增大優勢基因遺傳到子代的可能性，更符合遺傳進化規律；低適應度的個體以較高的概率進行變異操作，這樣就更容易通過變異操作產生新的優勢個體，避免算法陷入局部最優。通過自適應地調節遺傳操作中的交叉、變異概率，從而避免遺傳算法中早熟現象的出現。其中，遺傳操作的交叉概率Pc和變異概率Pm可以分別表示為：

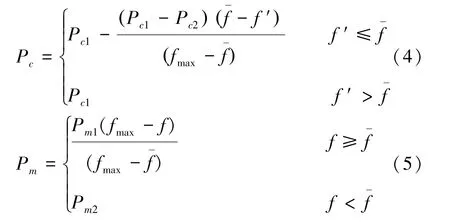
1.3 基于自適應遺傳算法的隨機森林回歸參數優化

以往的隨機森林回歸算法的參數優化多通過繪制學習曲線或網格搜索交叉驗證的方法實現，實施過程中恒定不變的搜索步長使得最優參數的獲取很難在速度和效果上同時達到最優。基于此，提出自適應遺傳算法輔助下的隨機森林回歸模型參數優化方法，利用遺傳算法優異的全局尋優能力，結合自適應方法動態調整的遺傳操作概率，達到快速取得全局最優解的目的。

隨機森林回歸是基于bagging 框架的決策樹模型，因此隨機森林回歸模型的參數調整包括2 部分：隨機森林框架的參數調優和決策樹的參數調優。使用自適應遺傳算法進行隨機森林回歸模型參數優化的流程如圖1 所示。

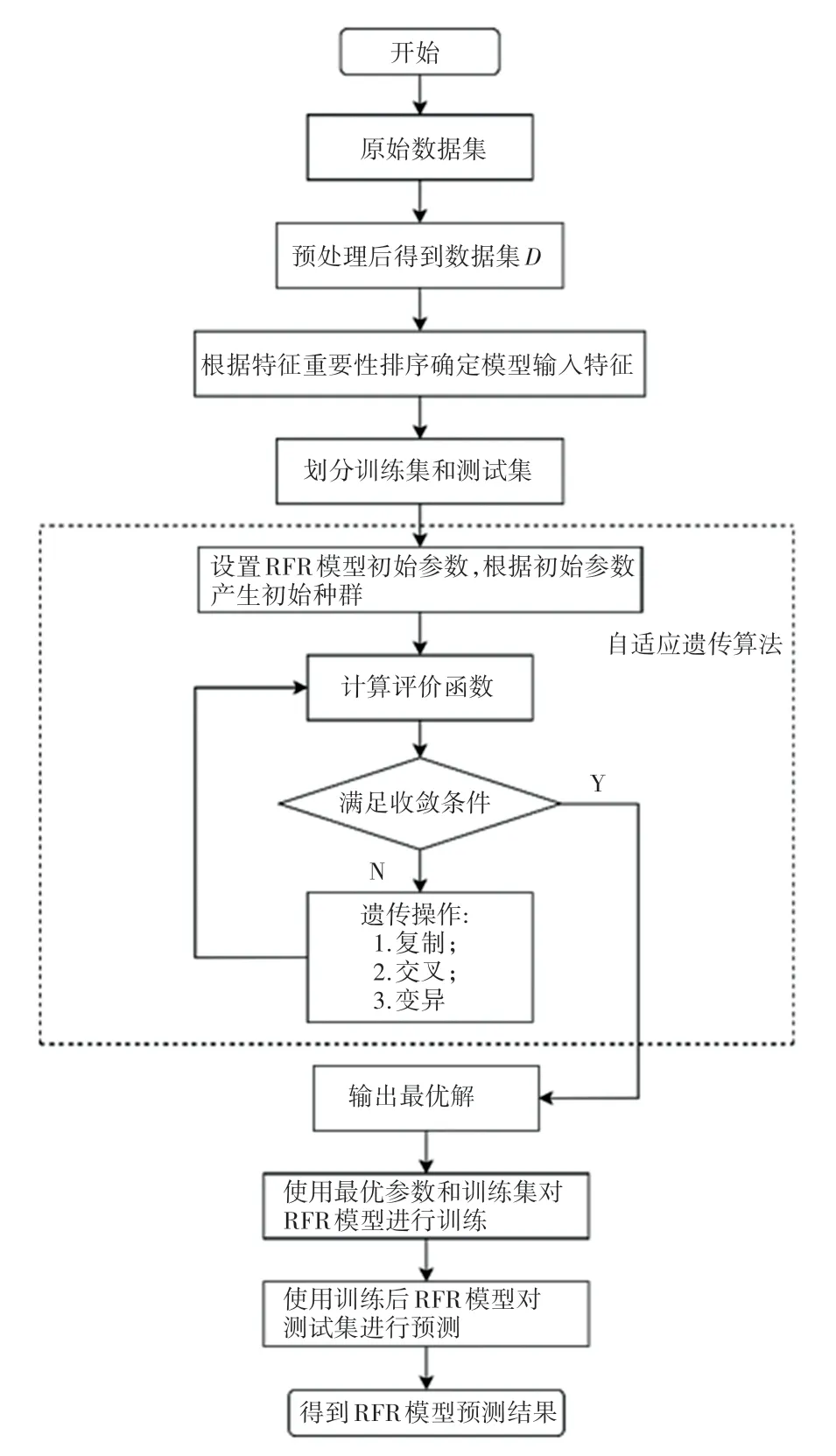
圖1 基于自適應遺傳算法的隨機森林回歸模型流程圖Fig. 1 Flow chart of Random Forest regression model based on adaptive genetic algorithm

2 實驗準備

2.1 數據集準備

為了驗證經自適應遺傳算法優化后的隨機森林回歸模型的有效性，使用Kaggle Boston house price數據集進行仿真驗證。數據集中的每一行數據都是對波士頓周邊或城鎮房價的情況描述，數據集共有14 個特征，分別為：城鎮人均犯罪率（CRIM）、住宅用地所占比例（ZN）、城鎮中非住宅用地所占比例（INDUS）、虛擬變量（CHAS），用于回歸分析；環保指數（NOX）、每棟住宅的房間數（RM）、1940 年以前建成的自住單位的比例（AGE）、距離5 個波士頓就業中心的加權距離（DIS）、距離高速公路的便利指數（RAD）、每一萬美元的不動產稅率（TAX）、城鎮中的教師／學生比例（PTRATIO）、城鎮中的黑人比例（B）、地區中有多少房東屬于低收入人群（LSTAT）、自住房屋房價（PRICE）。其中，PRICE為目標變量，其他13 個特征為模型的輸入自變量特征。各自變量特征的重要性見表1。由表1 可以發現，不論是RFR 模型、還是自適應遺傳算法優化后的AGA -RFR 算法模型，各自變量的重要性程度都是相近的，且RM和LASTAT都是對模型最重要的變量。

表1 模型特征變量重要性Tab.1 Importance of model characteristic variables

模型初始特征集中各項特征之間的相關性熱力圖如圖2 所示。圖2 中，部分特征間呈現負相關性，部分呈現正相關性。將Kaggle Boston house price 數據集按照7 ∶3 的比列劃分為訓練集和測試集。

圖2 模型特征相關性熱力圖Fig. 2 Model characteristic correlation thermodynamic diagram

2.2 評價指標

為了對比自適應遺傳算法參數優化方法的應用對隨機森林回歸模型預測精度的影響，需要對隨機森林回歸模型的預測精度進行評價。本文使用均方根誤差、決定系數和平均絕對誤差這3 個指標對模型的預測精度進行評價。對此擬給出研究分述如下。

（1）均方根誤差（Root Mean Squared Error，RMSE），也叫回歸系統的擬合標準差。由于均方根誤差對一組測量值中的特大或特小誤差反映非常敏感，所以，均方根誤差能夠很好地反映出測量的精密度。具體數學公式可寫為：

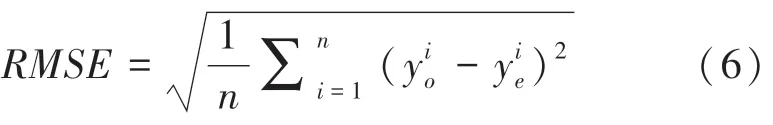
（2）決定系數（Coefficient of Determination，R2）。表示對模型進行線性回歸后，評價回歸模型系數的擬合優度。R2反映了模型因變量的全部變異能通過回歸模型被自變量解釋的比例。R2越大，線性回歸模型解釋的變異越大。具體數學公式可寫為：

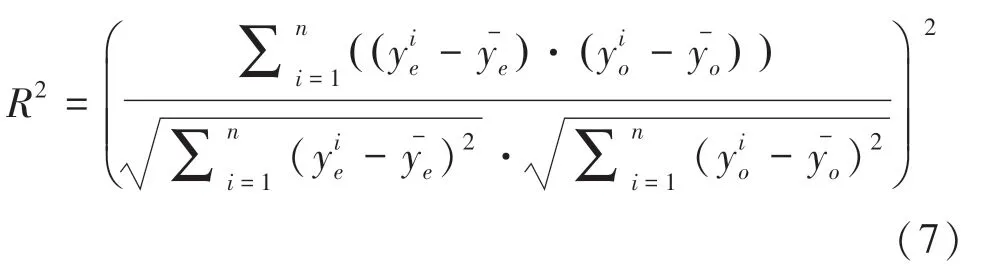
R2為1 時，表明模型預測值和真實值觀測值沒有任何誤差，表示回歸分析中自變量對因變量的解釋越好；R2為0 時，模型中樣本的每項預測值都等于均值；R2接近于0 時，表明模型預測能力差，預測效果接近于“使用觀測值的平均值作為模型預測值”。這就表示可能用了錯誤模型，或者模型假設不合理。

（3）平均絕對誤差（Mean Absolute Error，MAE）計算公式如下：

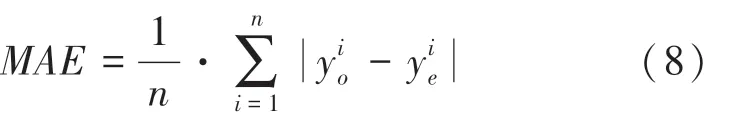
其中，MAE的取值范圍為 [0，＋∞），當預測值與真實值完全吻合時等于0，即完美模型；誤差越大，該值越大。

3 結果與分析

研究使用Kaggle Boston house price 訓練數據集對經過自適應遺傳算法優化得到的隨機森林回歸模型進行訓練，訓練后的模型對測試集進行預測。對比未經過參數優化的RFR 模型與經過參數優化的AGA-RFR模型的預測結果，預測效果對比見表2。

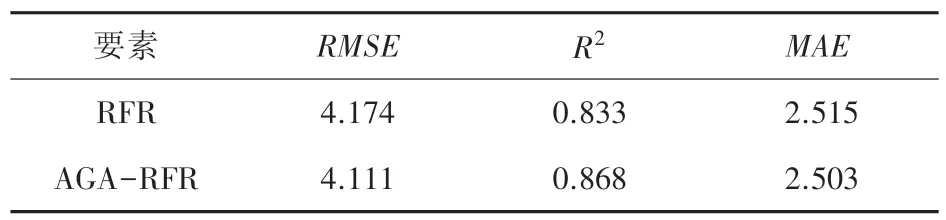
表2 模型預測精度對比Tab.2 Comparison of prediction accuracy of models

觀察表2 可以發現，經過自適應遺傳算法優化參數后的AGA-RFR 模型的回歸預測結果中，RMSE為4.111，優于RFR 的4.174；AGA-RFR 的R2為0.868，同樣優于RFR 的0.833；對比2 種模型的MAE也是同樣的情況。綜上可知，經過參數優化后的AGA-RFR 模型的MAE要優于RFR 模型。這就說明通過使用自適應遺傳算法對隨機森林回歸模型的參數進行優化，使得隨機森林回歸模型的預測效果得到了提高。

以Prices為橫坐標，Predicted prices為縱坐標，繪制出的模型預測價格與實際價格的對比結果圖如圖3 所示。

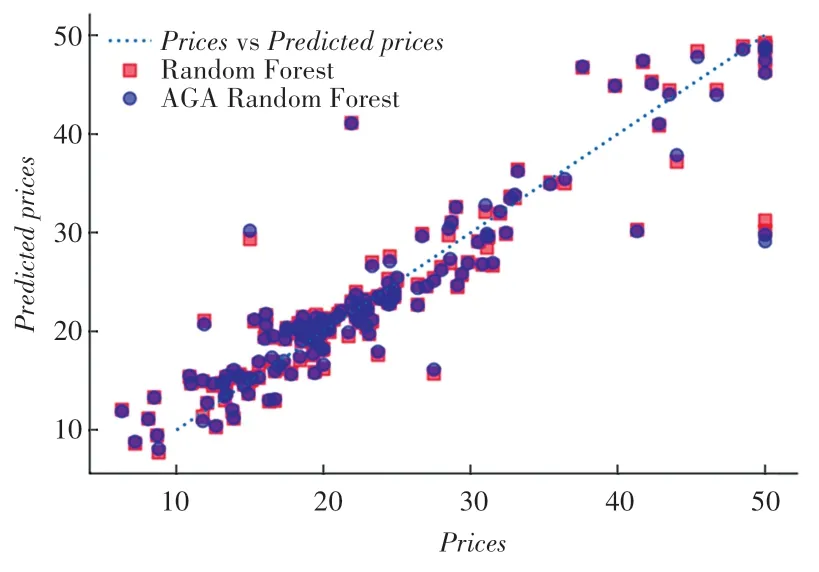
圖3 模型預測價格與實際價格對比圖Fig. 3 Comparison between model predicted prices and actual prices

由圖3 可知，相比于方形所代表的RFR 模型預測結果，圓形所代表的AGA-RFR 模型的預測結果總體上更接近于代表模型預測價格與實際價格相等的虛直線。由此說明，AGA-RFR 模型的預測結果比RFR 模型的預測結果更接近于真實價格。

模型預測值殘差與實際價格對比如圖4 所示。圖4 中，相比于方形所代表的RFR 模型預測結果，圓形所代表的AGA-RFR 模型的預測結果總體上更接近于代表預測殘差為0 的虛直線。這也說明，AGA-RFR 模型的預測結果比RFR 模型的預測結果具有更小的預測殘差。

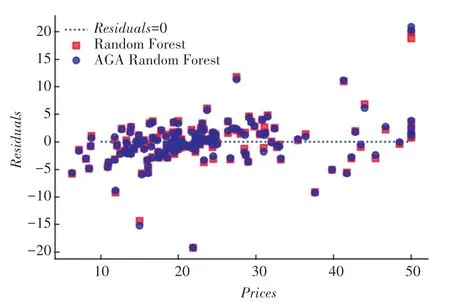
圖4 模型預測值殘差與實際價格對比圖Fig. 4 Comparison between residual error of model predicted value and actual prices

4 結束語

本文提出一種用于隨機森林回歸模型參數優化的方法，利用自適應遺傳算法在求解全局最優解的研究時不易陷入局部最優的優勢，通過對粒子的選擇、交叉和變異操作模擬生物界優勝劣汰、適者生存的過程。通過使用Boston house price 數據集對經過該方法優化后隨機森林模型的回歸預測效果進行驗證，試驗結果表明，經過該方法參數優化后的AGARFR 模型的回歸預測效果要優于未經過參數優化的RFR 模型的預測效果。

本文提出的基于自適應遺傳算法的隨機森林模型參數優化方法可以作為隨機森林回歸模型參數優化的一種有效手段。