基于稀疏矩陣的全聚焦陣列優化算法

高鐵成，王 昊，李 聰，遠桂民

（1．天津市光電檢測技術與系統重點實驗室，天津 300387；2．天津工業大學 電子與信息工程學院，天津 300387）

基于全矩陣數據采集（FMC）的全聚焦成像（TFM）相控陣超聲檢測技術具有成像分辨率高、對小缺陷靈敏度高的優點[1]。該算法可以在相控陣進行掃查時，依次激勵陣列內的每一陣元發射聲波，每一次發射后所有陣元進行接收，從而獲得檢測點的最大信息量，即相控陣可以利用每一發射-接收組合，根據給定的聚焦點，得到最佳的超聲檢測圖像。全聚焦成像技術極大地提高了相控陣掃查圖像的分辨率和可靠性。但是，全聚焦技術也存在著非常明顯的缺點，它的每一個采集周期都會產生N×N個A掃數據，不僅占用大量的內存而且減緩了掃查速度，很難滿足工業領域中快速成像的需求[2]。為了避免產生冗余數據，人們提出了稀疏化陣列的方法，在不明顯損失圖像質量的前提下，可以根據一定的原則選擇部分元素進行有效的檢測和成像，減少掃查數據量，從而提高成像效率。

近年來，大量科學家與學者利用基礎研究算法對全聚焦稀疏陣列進行設計，研究出一系列的優化方法[3]。Yang等[4]利用最小冗余陣列和遺傳算法對超聲相控陣二維稀疏陣列進行優化，所得陣列具有更好的一致性和性能；Yamashita等[5]在高分辨率超聲測量應用中通過多頻率激勵方式有效抑制了陣列柵瓣和旁瓣，同時增強了波束偏轉性能；Wilson等[6]提出了一種稀疏分布和周期分布相結合的混合波束形成方法，獲得了較好的分辨率和旁瓣水平；彭桃[7]采用稀疏陣列的方法在保證一定成像質量的前提下顯著提高全聚焦成像效率，并利用遺傳算法優化了稀疏陣列的成像性能。

本文運用了2種稀疏算法對陣列進行設計與優化，分別為最小冗余度陣列和遺傳算法。基于對以上2種算法的研究，本文建立了一種全聚焦超聲成像陣列的優化算法模型：首先，利用最小冗余陣列對相控陣列進行稀疏設計，既保證觀測中不出現偽像又做到孔徑最大（空間分辨率最高）的陣元分布。然后，利用遺傳算法對其掃查圖像信噪比進行優化，得到滿足條件的最佳陣列。將最終優化后的稀疏陣列與滿陣、最小冗余陣、遺傳算法優化陣列的聲場進行對比，并以此陣列為基礎設計相控陣探頭，建立全聚焦無損檢測掃查環境。通過對連續的20個點缺陷進行掃查測試，驗證此方法的可行性和有效性。

1 應用算法概述

1.1 最小冗余陣列

MRLA陣列的設計原則是使具有相同空域相關延遲的陣元傳感器對的數量盡可能少[8]。圖1為滿陣陣列分布及其空間采樣頻率示意圖。

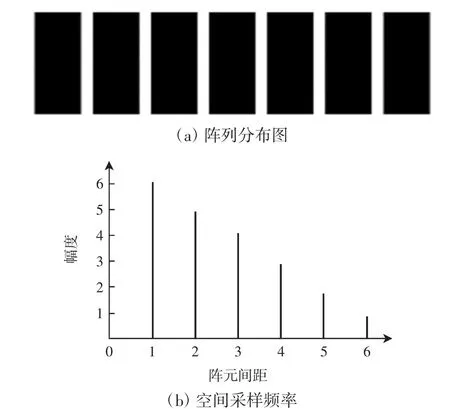
圖1 滿陣陣列分布及其空間采樣頻率示意Fig.1 Distribution of full array and its spatial sampling frequency

圖1（a）為一個7陣元的線性陣列分布圖（黑色表示為此處有陣元），圖1（b）為該陣列的空間采樣頻率圖，在橫坐標為1處，幅值為6，意思是在該陣列中，陣元間距為1的組合有6組；在橫坐標為6處，幅值為1，意思是陣元間距為6的組合有1組。只有增大空間采樣頻率的長度，使得每種間距（大于等于1）的組合數目都最接近1（不能小于1）時，該陣列才做到冗余度最小[9]。

圖2為最小冗余度陣列分布及其空間采樣頻率示意圖。

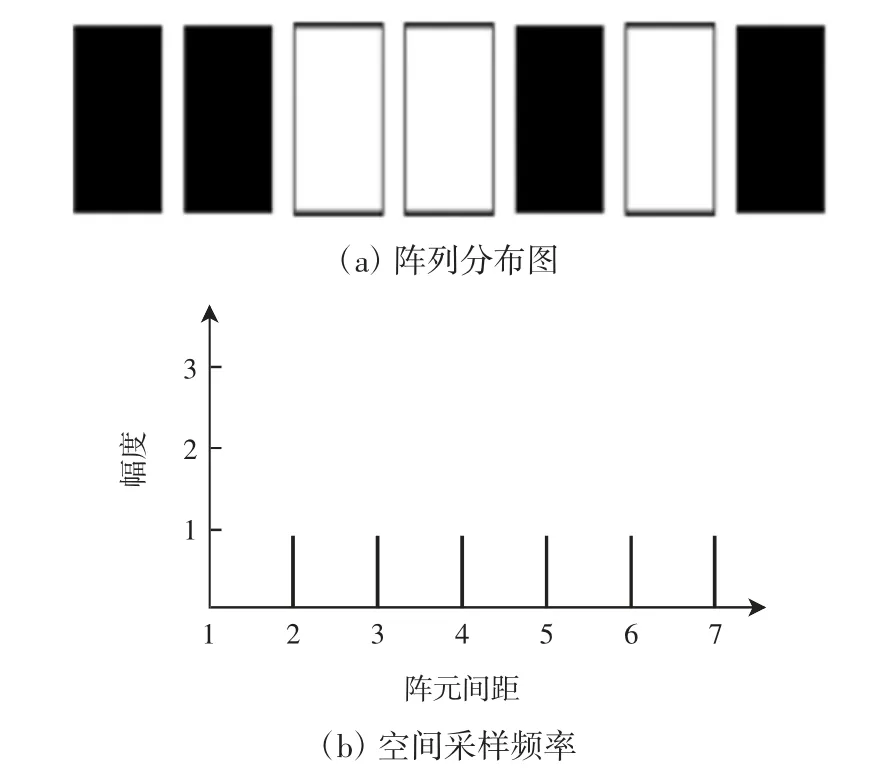
圖2 最小冗余度陣列分布及其空間采樣頻率示意Fig.2 Distribution of MRLA and its spatial sampling frequency

用歸一化的矢量uk來表示一個滿陣為M含有N個陣元的最小冗余線性陣列的陣元位置分布。圖2（a）中，黑色表示該位置有陣元，白色表示沒有陣元。此時，陣列可表示為{1，1，0，0，1，0，1}，或以陣列的第一個陣元作為參考點，令u1=0，可表示為{0，1，4，6}，即在陣列中0、1、4、6的位置分別有一個陣元，其他位置無陣元。此時，它的陣列孔徑長度等于一個7陣元的均勻線性陣列，其空間采樣頻率如圖2（b）所示。

陣列的冗余度R為：在空間采樣頻率Z中，除去第一個元素外，其余大于1的元素中，超過1的數值之和。在此陣列中，除去4外，其他都是1，所以冗余度最終為0。對于一個最小冗余度陣列，空間采樣頻率Z中應該沒有0值（沒有空洞），而且冗余度R應小于等于冗余度的最大允許值B，即：

陣元間相關函數只與陣元間的位置差di，j=uj-ui（其中0≤i≤j≤M-1）有關，即陣元間的位置差di，j是大于等于0的自然數，此時所有陣元位置差的集合為

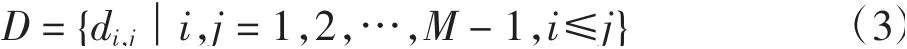
基于上述假設，最小冗余陣列的設計問題可以通過下面的約束優化問題來描述：

式中：R表示陣列的最小冗余度；L代表孔徑數。當L較小時，可以通過窮舉法進行計算，隨著L的變大，會極大地增加計算，可以通過編程方法減少計算量。

圖3所示為計算稀疏陣列及冗余度的程序流程圖。

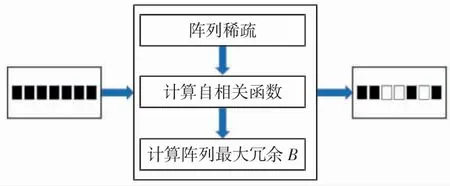
圖3 最小冗余度陣列計算流程Fig.3 Calculation flow of MRLA

根據圖3流程可求得部分最小冗余度陣列，如表1所示。

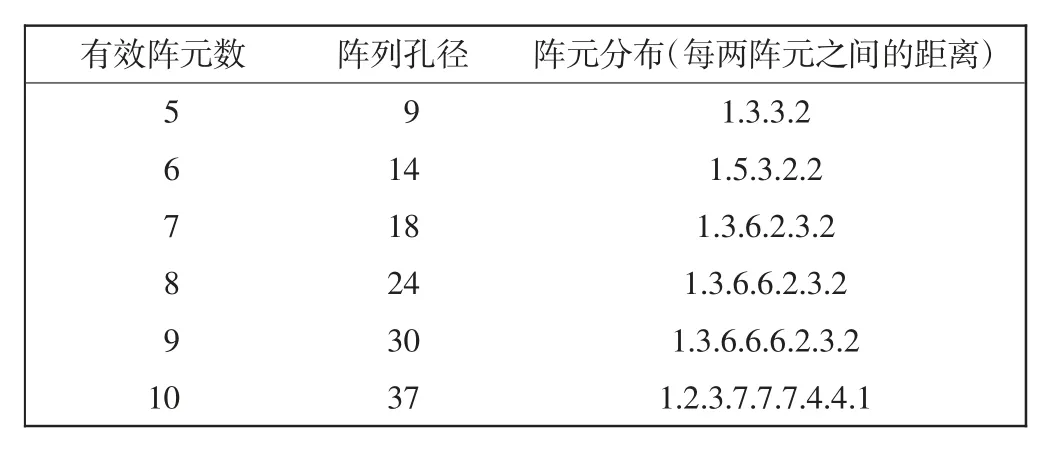
表1 部分最小冗余陣列（MRLA）Tab.1 Partial MRLA

1.2 遺傳算法

在稀疏相控陣列的問題求解中，可以將滿足一定要求的不同陣列看作自然界中的一個種群[10]，其中的每一個特定陣列看作一個個體，在迭代前我們需要明確一些要素[11]。

（1）個體適應度評價：個體適應度一般采用比例選擇的方式計算迭代過程中保留下來的個體數目，因此，為了合理確定每個個體的保留幾率，一般需要保證個體的適應度值為非負數[12]。

一般地，通過以下2種情況來確定個體適應度函數，能夠保證函數取值不為負數[13]。

首先，如果最優解問題為最小化的情況時，可以通過以下方式來轉換：

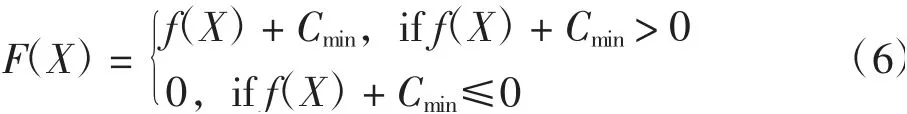
Cmin為一個較小的調整參數，通常可根據優化問題人為設置或設置為迭代過程中目標函數出現的最小的值[14]。

其次，如果最優解問題為最大化的情況時，可以通過以下方式來轉換：

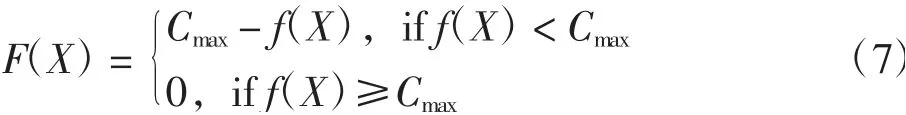
式中：Cmax為一個較小的調整參數，通常可根據優化問題人為設置或設置為迭代過程中目標函數出現的最小的值[15]。

算法的適應度函數需要計算每個陣列的峰值旁瓣水平[16]。將陣元當作各向同性的點源，則具有N個陣元的稀疏陣列的波束E（u）可以表示為：

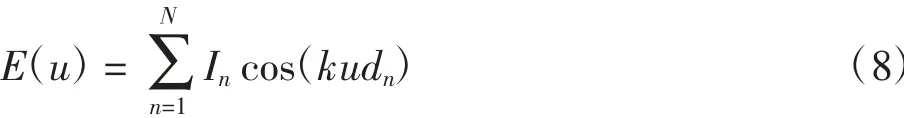
式中：dn和In分別表示陣元的坐標和激勵振幅；u=cos（θ）；θ為波束的偏轉角度。本文中所設計的每個陣元幅度均相等，即In=1，同時d1=0，dN=L，因此公式（8）可以簡化為：

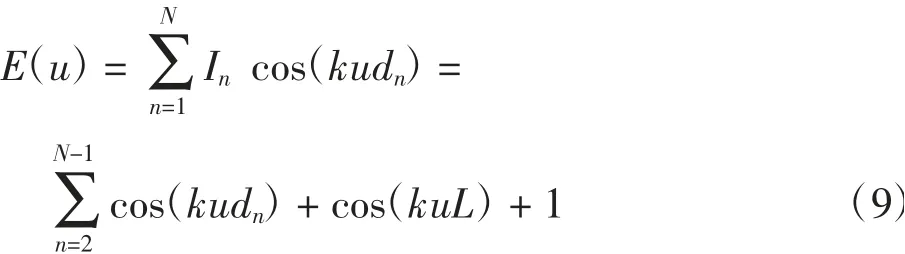
算法優化的目標為最小化稀疏陣列的峰值旁瓣水平[17]，因此，根據陣列峰值旁瓣的含義，遺傳算法的適應度函數可以定義為：

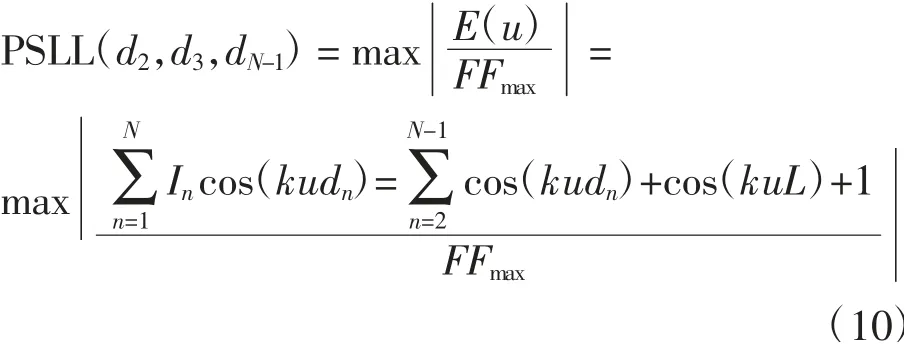
式中：FFmax為波束主瓣的峰值。為了得到具有最小峰值旁瓣水平的稀疏陣列，定義目標函數為：

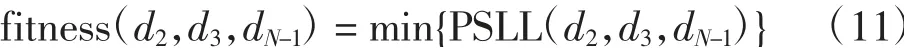
（2）基本遺傳算法的優化參數。通常，需要根據具體的優化問題預先設置種群規模、迭代步數、交叉概率和變異概率這4個優化參數[18]：M為種群規模，表示參與種群進化的個體數量，取值范圍20～100；T為迭代步數，表示算法迭代的最大次數，取值范圍100～500；Pc為交叉概率，取值范圍0.4～0.99；Pm為變異概率，取值范圍0.000 1～0.100 0。

4個參數之間相互制約，共同影響著遺傳算法的搜索性能[19]和運算結果，因此在實際優化問題中，需要結合最優解問題[20]的特點和具體要求，通過不斷嘗試，綜合考慮各項參數的設置。遺傳算法運算示意圖如圖4所示。

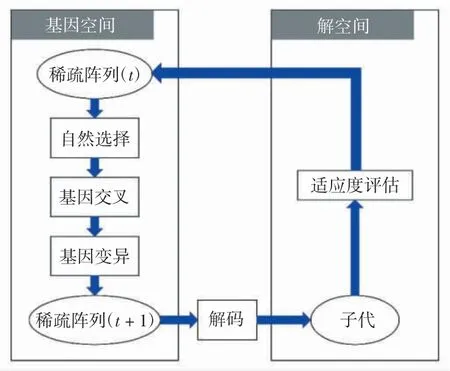
圖4 遺傳算法運算過程示意圖Fig.4 Operation process of genetic algorithm

2 算法綜合

2.1 單算法波束圖仿真

最小冗余度陣列實質上是在陣元數目一定的情況下，既保證獲取信息量的冗余值最小又做到孔徑最大（空間分辨率最高）的陣元分布。根據上述流程求得滿陣數7稀疏陣元數4的最小冗余度陣列為{1，1，0，0，1，0，1}，其聲場波束圖與滿陣進行對比如圖5所示。

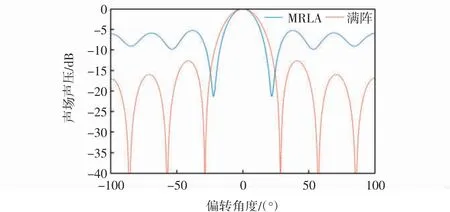
圖5 最小冗余度陣列波束圖Fig.5 MRLA beam pattern

由圖5可知，稀疏后的陣列因為陣元間距增大，主瓣寬度隨之變窄，提高了橫向分辨率。但是稀疏陣列減少了陣元數目，旁瓣增大，有可能出現圖像模糊、偽像等現象。

為了驗證遺傳算法對稀疏陣列求解的優化性能，必須從可能的大量陣列中選擇最好或者較好的結果。圖6為3組不同稀疏陣列的優化仿真結果。

從圖6中可以看出，采用論文中介紹的遺傳優化方法及相關參數，在對7選4、27選6以及32選20這3種稀疏陣列的優化中，均能夠較快地獲得最優的陣列分布，通過對優化陣列進行波束圖仿真，優化后的陣列波束具有良好的旁瓣特性。

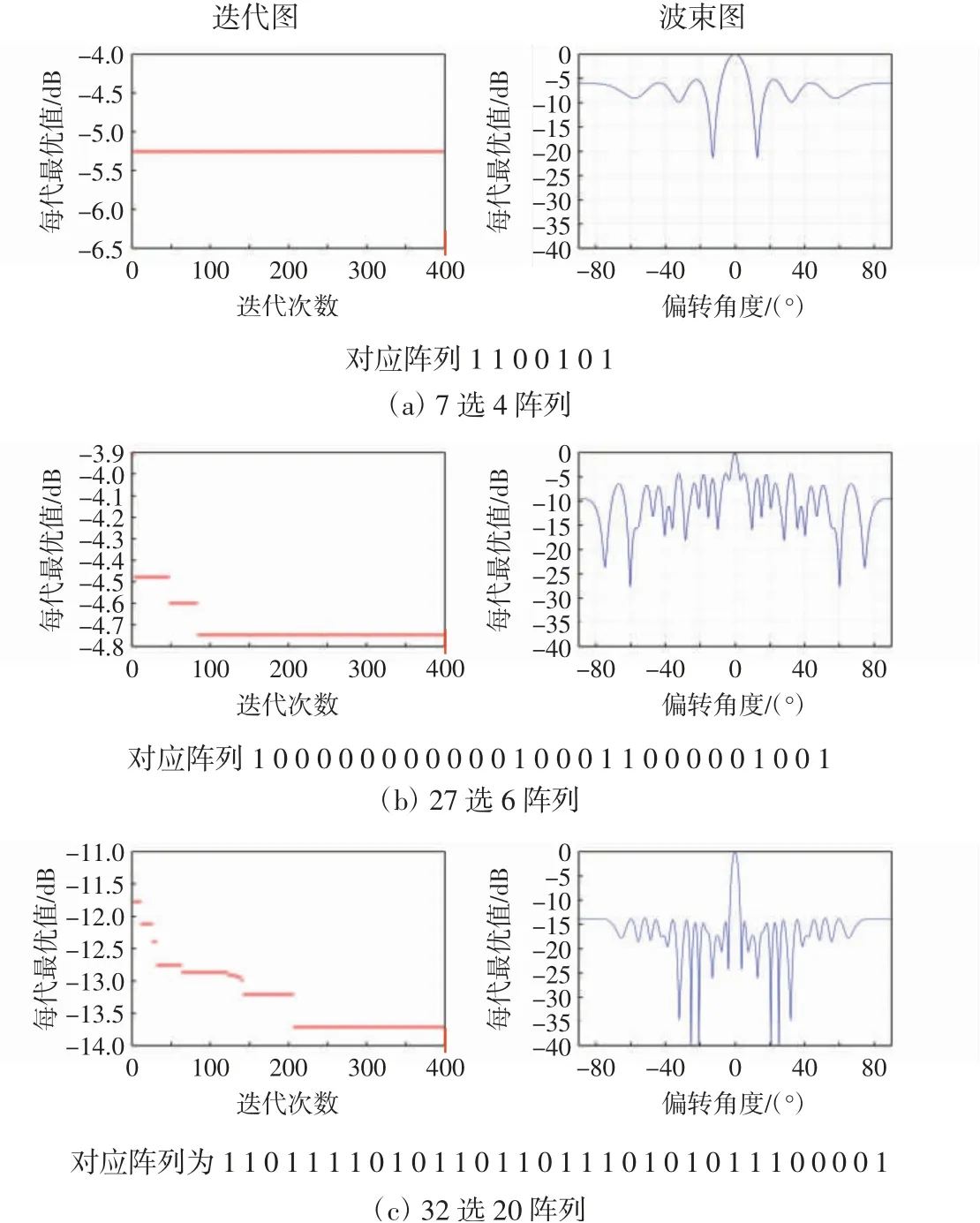
圖6 遺傳算法優化陣列仿真結果Fig.6 Simulation results of optimization of array by GA

2.2 算法綜合仿真

基于上述2種稀疏陣列算法，若單獨使用最小冗余陣列，得到的稀疏陣列則可以獲取冗余度信息最小情況下的最大信息量，但是只是在對陣列進行分析的層面，這會導致稀疏后的陣列超聲旁瓣過大，圖像模糊，甚至容易出現偽像；若單獨使用遺傳算法稀疏陣列，則可以得到要求下的最優陣列，具有良好的旁瓣特性，但是沒有考慮空間采樣頻率，得到的圖像容易出現遺漏信息。本文將2種算法進行綜合使用，利用最小冗余度陣列對陣列進行稀疏設計，利用遺傳算法對其掃查圖像信噪比進行優化，這樣得到的圖像既可獲得最小冗余下的最大信息量又具有良好的旁瓣特性，同時陣列稀疏化，可以極大地提高全聚焦掃查速率，如圖7所示。

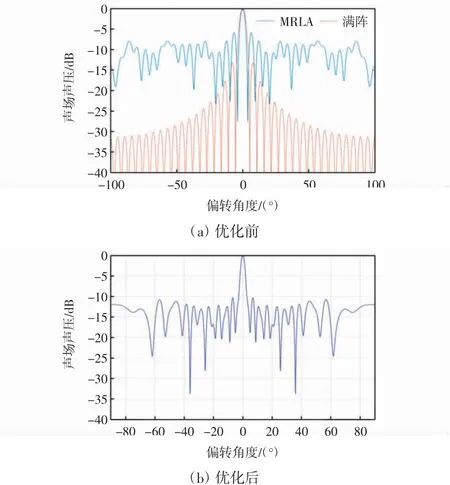
圖7 陣列優化對比Fig.7 Comparison chart of array optimization

以37陣元滿陣基礎上設計16有效陣元地稀疏陣列問題為例，參考表1中第6行陣列（11010010000 00100000010000001000100011），首先利用最小冗余度陣列確定16個陣元中的10個，此時稀疏陣列優化問題變成在27個位置中放置其余地6個陣元。在27選6的優化設計中，利用遺傳算法進行求解，程序求得陣列為1101011001010100101010001001000100011。圖7（a）所示，MRLA標識圖線為最小冗余度陣列聲壓波束圖，此時最高旁瓣為-5.856 8 dB。圖7（b）為遺傳算法優化后的陣列，此時最高旁瓣為-10.759 6 dB，明顯優于最小冗余陣列。

2.3 算法對比

粒子群算法（PSO）同樣是一種仿生全局優化算法，主要模擬鳥類覓食、人類社會行為而提出，該算法實現簡單，在解決非線性問題中有著較好的表現。將37選16優化前的陣列利用粒子算法進行稀疏的陣列聲壓圖如圖8所示。

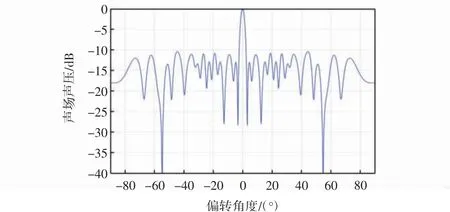
圖8 PSO優化陣列波束圖Fig.8 Beam pattern of PSO optimized array

由圖8可知，稀疏陣列的最高旁瓣-10.429 2 dB，優化效果略差于GA算法。而且PSO算法有著收斂過快、易收斂于局部極值的特性，本文所得到的稀疏陣列最后需要用于全聚焦掃查，算法應該具有可靠性，PSO算法未經改進的情況下不適宜用于多陣列的稀疏情況。本文所設計的稀疏優化算法可以完全避免出現只優化為局部極值的情況。

3 掃查試驗測試

為了驗證稀疏陣列算法對于改善全聚焦成像效率的有效性，本文建立了一個全聚焦相控陣超聲檢測環境，除探頭內陣列稀疏化方式不同外，其余參數皆設置為固定值，如表2所示。

表2 超聲探頭參數表Tab.2 Ultrasonic probe parameters

取3組陣列進行對比測試：A為16有效陣元最小冗余陣列（滿陣37陣元）；B為遺傳算法優化后的稀疏陣列；C為37陣元滿陣陣列。掃查目標為連續的20個點缺陷，測試結果如圖9所示。

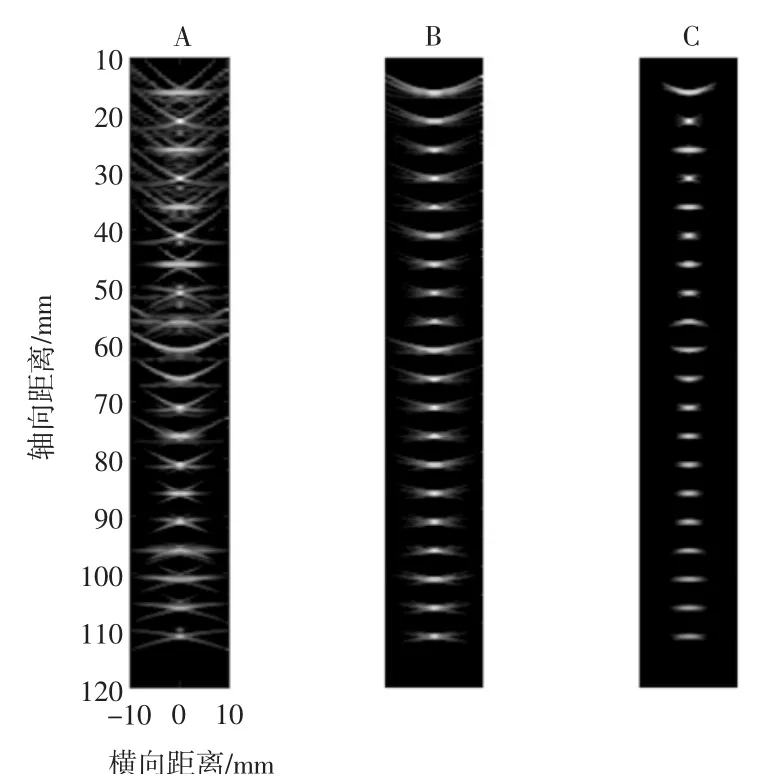
圖9 點缺陷掃查圖Fig.9 Scanning chart of point defects

從圖9中看出，滿陣陣列C圖像清晰，缺陷位置、狀態明顯可辨，其余部分的噪聲情況也有很好的水平，最小冗余陣列A盡管仍可以較清晰地分辨出缺陷的個數和位置，但是圖像中存在明顯的偽影，形態模糊，而通過遺傳算法優化后的稀疏陣列B掃查的圖像有較為明顯的優化，檢測圖像的信噪比有明顯的提高，符合上述分析，最小冗余陣列可以捕獲到最小冗余信息下的最大信息量，但是旁瓣增高，有可能出現圖像模糊、偽影等現象，而優化后的圖像有良好的旁瓣特性，雖然沒有滿陣陣列的圖像清晰，但是在不產生噪聲偽影的情況下可以極大地提高掃查效率。

4 陣列優化分析

對一個全聚焦陣列最為直觀的評價參數即為其掃查效率，不同稀疏度的陣列對掃查效率有著決定性的影響，陣列稀疏化越大，相比于滿陣的掃查越快，但是圖像質量也會明顯降低。保持除陣列稀疏率之外的其他參數不變，不考慮圖像中缺陷點的成像質量，按照上述掃查過程記錄各個陣列的時間，以滿陣為基準的百分比統計結果如圖10所示。

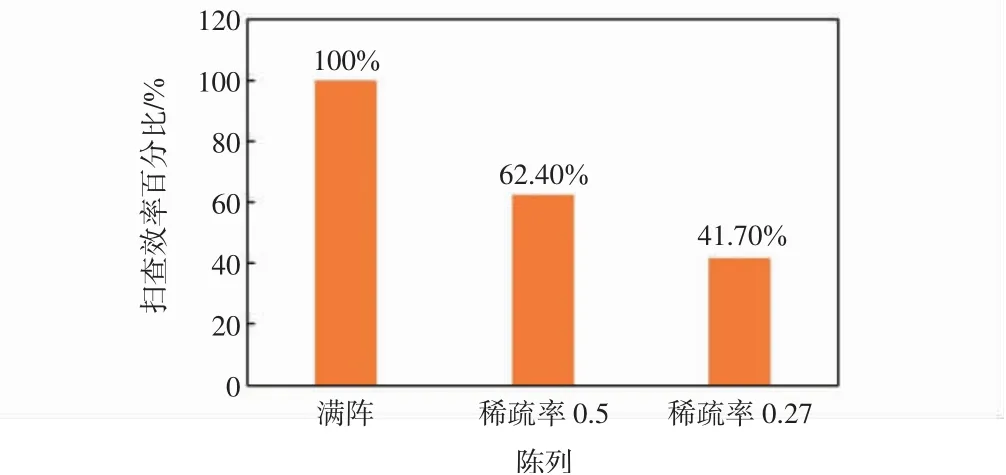
圖10 掃查效率Fig.10 Scanning efficiency

由圖10可知，由于陣列中陣元數目的減少使得計算數據量大幅度降低，很大程度上提高了掃查效率，全聚焦實時掃查得以實現，稀疏率為0.27的陣列較滿陣成像效率提高了58.3%，說明了在全聚焦成像中采用陣列稀疏化方法的有效性。

針對陣列評價本文引入一個參數API，它是表征陣列波束點擴散函數的空間大小的一個無量綱值。API的大小定義為：點擴散函數中幅度高于最高賦值的-6 dB的區域面積A-6dB，并以波長的平方進行歸一化。API數值越小，表明檢測分辨率越高。表3列出了陣列API值。

表3 陣列API值Tab.3 API value of array

由表3可見，隨著對陣列進行稀疏化處理，陣列API值也會相應地小幅度增大。API的小幅度增大在一定范圍內不會對掃查成像造成影響。但是，當稀疏率低于0.27時，API會急劇增大，掃查分辨率會有極大程度的降低。

5 結論

本文將陣列稀疏化方法應用于全聚焦成像技術中，研究了全聚焦超聲相控陣列的優化問題。傳統的FMC技術需要采集所有的A掃信號，因此它的圖像中包含了陣列所能檢測的最大信息量，會極大程度地減緩掃查速度。本文提出了一種稀疏矩陣全聚焦超聲成像算法模型，利用最小冗余陣列對相控陣列進行稀疏設計，利用遺傳算法對其掃查圖像信噪比進行優化。通過對比波束圖和采用稀疏陣列對單點缺陷進行掃查成像，證明37稀疏16陣列利用此算法稀疏后最高旁瓣有4.902 8 dB的優化；對于多陣列的稀疏優化，GA算法比PSO算法更具有可靠性；稀疏率為0.27的陣列相比于滿陣其成像效率有58.3%的提高，且API值為0.539 7，不會對缺陷成像造成較大影響。