ATS算法在四輪獨立轉向的時間同步研究 *

肖廣兵，季 淦，孫 寧，張 涌，陳 勇

(1. 南京林業大學 汽車與交通工程學院，江蘇 南京 210037；2. 南京林業大學 機械與電子工程學院，江蘇 南京 210037)

0 引 言

四輪獨立轉向作為分布式汽車控制的核心技術之一，可提高汽車高速操縱穩定性和低速機動性，是未來智能汽車領域的重要發展方向。通常情況下，四輪獨立轉向系統由車輪轉角傳感器、車載電子控制單元(electronic control unit, ECU)和4個獨立轉向輪構成。ECU用于計算獨立輪狀態并通過國際標準化的串行通信協議控制器局域網絡(controller area network, CAN)傳輸轉向指令[1]。由于每個獨立轉向車輪配有獨立驅動系統，車輪之間沒有機械連接，車輛可實現對每個車輪運動狀態的獨立控制。具體而言，在駕駛員通過操縱方向盤做出轉向動作后，ECU決策輸出4個控制信號，通過CAN分別傳送給4個轉向電機，從而實現對車輛的轉向控制。轉向過程中，4個轉向輪需要協同合作完成車輛轉向操作。然而在分布式CAN網絡中，每個輪轂電機的本地時間受溫度、噪聲、電源等環境條件影響，往往存在一定偏差，存在對ECU控制信號響應不同步的問題，這將會導致車輛產生轉向偏差，甚至引發嚴重的交通安全事故。

為實現四輪獨立轉向的時間同步，通常將每個轉向輪分別與ECU進行同步，但由于控制指令在CAN網絡中存在著優先等級劃分，高優先級指令會先于低優先級指令進行傳輸，這使得四輪獨立轉向指令在傳輸過程中產生了非對稱延時，該方案可能使得每個轉向輪本地時間振蕩發散，即某一轉向輪同步后的時間(T1)與另一轉向輪同步后的時間(T2)不相等；且在多輪通信過后，兩者差值越來越大，未能從根本上解決獨立同步轉向中節點的時間同步問題。

筆者以四輪獨立轉向時車載CAN網絡時間同步過程為應用背景，對現有主流時間同步方法，即平均時間同步法(average timeSynch, ATS)[2]在分布式輪轂電機時間同步過程中的性能進行評估。從數學角度對ATS算法的收斂過程進行推演，證明了在車載CAN網絡中使用ATS算法會使得分布式轉向輪轂電機時間同步失效，闡明了ATS算法在具有非對稱延時的車載CAN網絡中的發散特性[2]。此外，為抑制四輪獨立轉向過程中時間同步的發散性，筆者對造成ATS算法在非對稱時間延遲下的發散因子進行分析，在不改變原有算法思路前提下對發散因子所對應參數進行修正，通過公式推導、仿真和實車試驗對結果進行驗證，為ATS算法在四輪獨立轉向系統中的時間同步提供思路。

1 研究進展

為使執行器在車載CAN網絡中保持一致運動，學界對CAN網絡時間同步進行了很多研究[3-9]，例如：G. R. BOSCH[10]認為在CAN協議規范中，CAN協議支持錯誤檢測機制，當檢測到報文傳輸失敗時會將報文進行重新傳輸；K. TINDELL等[11]分析了CAN網絡響應時間，評估了消息最壞情況下的響應時間，從而使得消息具有實時性，但該方法只解決了報文在離開時間到期之前失效問題，保證了報文在一定時間內不會被丟失，而時間同步的問題仍沒得到有效解決。

硬件集成也是目前CAN常用的一種時間同步方式，其實質是將多個設備集成到一個CAN中進行監視和調整執行器本地時鐘。例如：G. RODRGUEZ-NAVAS等[12]開發了一種用于CAN時間同步的正交硬件，可提供一種時鐘同步服務，通過對分布式系統中當前實時的兩種范式比較，實現高精度時間同步；G. BREABAN等[13]提出了CAN基于GALS的MPSoC時鐘同步方法，它包含了用于CAN控制器的HW/SW混合設計以實現同步；G. RODRGUEZ-NAVAS等[14]通過OCS-CAN使用改進的CAN控制器對每幀的特定位置執行信號處理，以實現節點之間的精確偏移，從而消除了因網絡抖動和消息處理抖動引起的不確定性影響。

目前亟需解決硬件同步的高成本和需要支持的嵌入式軟件的問題，故基于軟件的時間同步算法成為當下的研究熱點。JIAO Ji[15]針對CAN提出了一種非主從時鐘同步算法，該算法為使信號傳輸不受網絡信息影響，將傳輸的同步信號放在單獨的信道中；I. BROSTER等[16]提出了一種基于CAN的協議，該協議犧牲了錯誤消息而不具有及時性，它通過指示丟失非致命錯誤消息來證明CAN時間同步方法的可行性，且系統可繼續正常運行而不會出現錯誤消息；楊福宇[17]提出了一種為CAN設計的新時鐘同步算法，該算法減少了同步期間發送的消息，選取同步需要的若干個節點，實現微秒級數量的同步精度和準確性。但當前軟件同步均沒考慮存在非對稱時間延遲的網絡情況。

2 數學建模

考慮一個四輪獨立轉向系統G={N,E}，其中：節點集合N={ni,i≤5,i∈Z+}表示掛載在CAN網絡上的通信節點，包含一個ECU單元和4個輪轂電機控制單元；邊緣集合E表示節點之間在CAN網絡中的通信鏈路。ECU通過周期性發送報文與4個輪轂電機交互。報文包含了車輛轉向過程中相關控制信息，如車輛轉向控制信息、轉向角度等，同時還包含了發送節點本地時間以保證掛載在CAN網絡上所有節點能對時間進行同步，實現車輛協同轉向。從車載電子控制單元ECU發送消息到前后轉向輪示意如圖1。

圖1 從車載電子控制單元ECU發送消息到前后轉向輪Fig. 1 Sending a message from the in-vehicle electronic control unitto the front and rear steering wheels

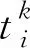
(1)

每個節點周期性地廣播報文與其他節點進行信息交互，并根據接收到其他節點的本地時間讀數對自身本地時間進行估計、調整，并與其他節點進行時間同步。對于節點ni有式(2)：

(2)

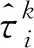
對于任意ε>0，且兩個節點i、j滿足式(3)時，則認為CAN網絡完成了時間同步：

(3)

3 ATS算法推算演化

3.1 ATS算法時間同步

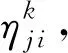
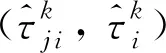
圖2 ATS算法Fig. 2 ATS algorithm

3.2 非對稱時間延遲下時間同步發散

考慮收發器對信號響應、信號優先級及信號在通信介質上的傳輸時間等原因，節點之間的報文傳輸存在一定時間延遲。由于報文交互過程中數據沖突、優先級等原因，ECU到4個輪轂電機控制單元的通信延遲并不是完全一致。筆者通過反證法證明了在非對稱時間延遲條件下，時鐘同步過程中的發散特性。

(4)

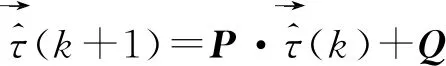
(5)

式中：P和Q分別為不同的2×2矩陣。

(6)

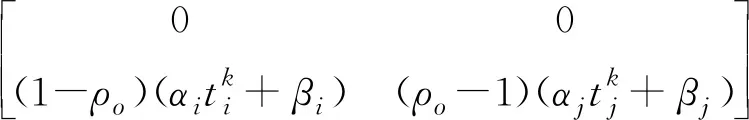
(7)

假設同步過程中，節點ni在第k+1輪里率先更新成為參考節點，則在式(6)、式(7)中應當用Pα(k+1)和Qα(k+1)來表示，由此可得：

Qα(k+1)=

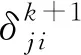
經整理可得式(8)：

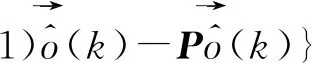
(8)

為方便觀察，用B(k+1)表示式(8)中的[K+1]Pα(k+1)+Qα(k+1)-P[K]，則有式(9)：

(9)

證明中需用到的兩個定理。

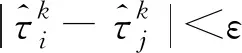
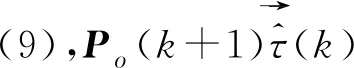
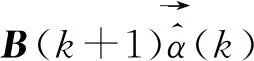
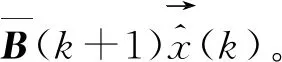
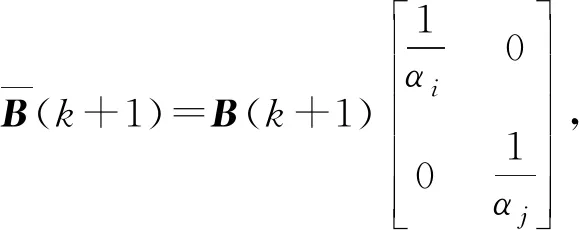
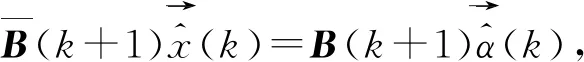
(10)

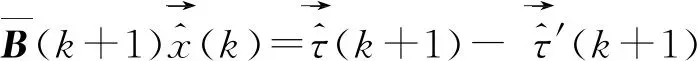
(11)

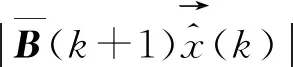
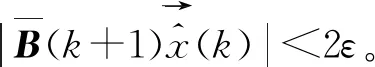
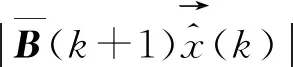
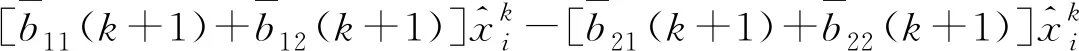
(12)

上述計算過程只純粹涉及到ATS算法的推導，時間是否同步不得而知，對此應增添新的假設情況。

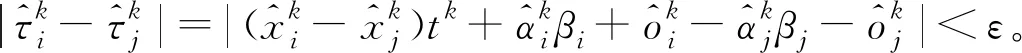
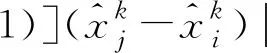
由此可得結論：隨時間推移，傳統ATS算法在四輪獨立轉向系統CAN網絡中無法達到收斂結果。

3.3 時間同步發散因子

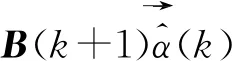
1929年施蟄存在中國第一次運用心理分析創作小說《鳩摩羅什》、《將軍底頭》而成為中國現代小說的奠基人之一。1930年他主編的《現代》雜志，引進現代主義思潮，推崇現代意識的文學創作，在當時影響廣泛。抗日戰爭爆發后，他曾先后執教于云南大學、廈門大學、暨南大學和光華大學。1952年以后他任教于上海華東師范大學中文系。20世紀80年代，由于現代主義思潮的重新涌入中國，他的文學創作才又重新開始受到重視。

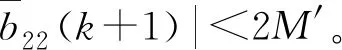
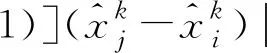
4 模擬仿真

4.1 仿真設置

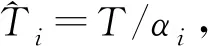
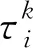
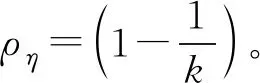
為衡量網絡中ATS算法的時間同步質量，定義3個指標：時間偏差d、時間偏差均值Rk和時間偏差方差Dk。

4.1.1 定義1

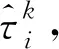
(13)

定義1的時間偏差d與式(3)ATS算法的目標函數相近，通過觀察每輪循環后d值絕對值大小，可直觀地得出ATS算法時間同步的質量。也就是說，當d的絕對值隨著時間推移越來越小，即證明ATS算法時間同步質量好，反之則差。

4.1.2 定義2

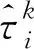
(14)

時間偏差均值Rk得到了每個時刻節點的估計時間與絕對時間的偏差，該數值大小反應了兩個節點通過ATS算法調整后整體估計時間較真實時間的快慢，Rk越大代表調整過后兩個節點較真實時間越快，反之則越小。

4.1.3 定義3

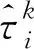
(15)

時間偏差方差Dk可用來觀察兩個節點較真實時間的變化規律。當Dk隨絕對時間變化越來越大，表示兩個節點估計時間與真實時間偏差的變化率越來越大，即該時刻下節點估計時間的調整越大，變相驗證了Rk變化的正確性。

4.2 仿真驗證

設置漂移速度和初始偏移量都不相同的兩個節點ni和nj，其中節點ni的本地時間漂移速度αi=1，初始漂移量βi=0.1；節點nj本地時間漂移速度αj=0.998 9，初始偏移量βj=0.3。在仿真中增加不存在非對稱通信延遲情況，對提出的3個指標在存在非對稱通信延遲情況下進行實驗。圖3、圖4描述了兩個節點進行2 000次通信的時間同步質量，橫坐標代表同步進行的循環次數。圖3和圖4(a)縱坐標表示兩節點時間偏差d，單位：s；圖4(b)縱坐標表示時間偏差均值R，單位：s；圖4(c)縱坐標表示時間偏差方差D，單位：s2。

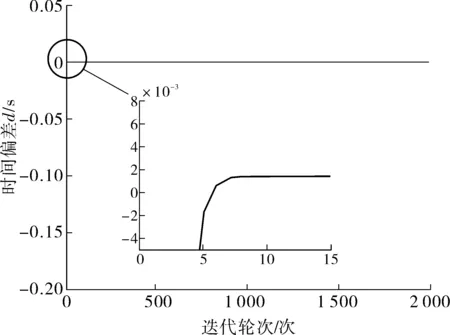
圖3 兩節點在沒有非對稱延遲下使用ATS算法進行2 000次通信后的時間差值Fig. 3 The time difference between two nodes using the ATSalgorithm for communicating 2 000 times without asymmetric delay

從圖4可知：在初始時間偏差為βj-βi=0.2，且不存在非對稱通信延遲情況下，使用ATS算法能在9個通信輪次內使兩個節點的時間偏差縮小至0.001 5 s，從而實現同步；存在非對稱通信延遲且在(0, 0.01)隨機數情況下，隨著迭代輪次增加，節點間的時間偏差d整體上以0為震蕩中心呈發散的趨勢越來越大。

以本次仿真為例，當迭代輪次進行到第1 930次時，兩節點時間偏差值d最大，dmax=6.43 s。不僅如此，平均每個節點估計時間與真實時間差值整體上也以震蕩發散的形式越來越大。由圖4(b)可發現：震蕩幅度迭代在第1 995～2 000次時達到最大，幅值為3.42 s。而時間偏差均值R在仿真的第1 989次迭代輪次下數值最大，誤差為56 s。由圖4(c)中時間偏差方差D不斷擴大也印證該現象。同樣，D值整體呈震蕩發散形式不斷增大，在第1 811次迭代時達到最大值Dmax=0.006 249 s2。

兩節點使用改變權重系數ρη的ATS算法在非對稱時延下進行2 000次通信后的時間差值如圖5。

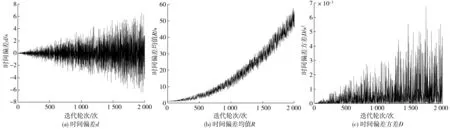
圖4 兩節點在ATS算法下進行2 000次通信的數值Fig. 4 The value of the two nodes communicating 2 000 times under the ATS algorithm

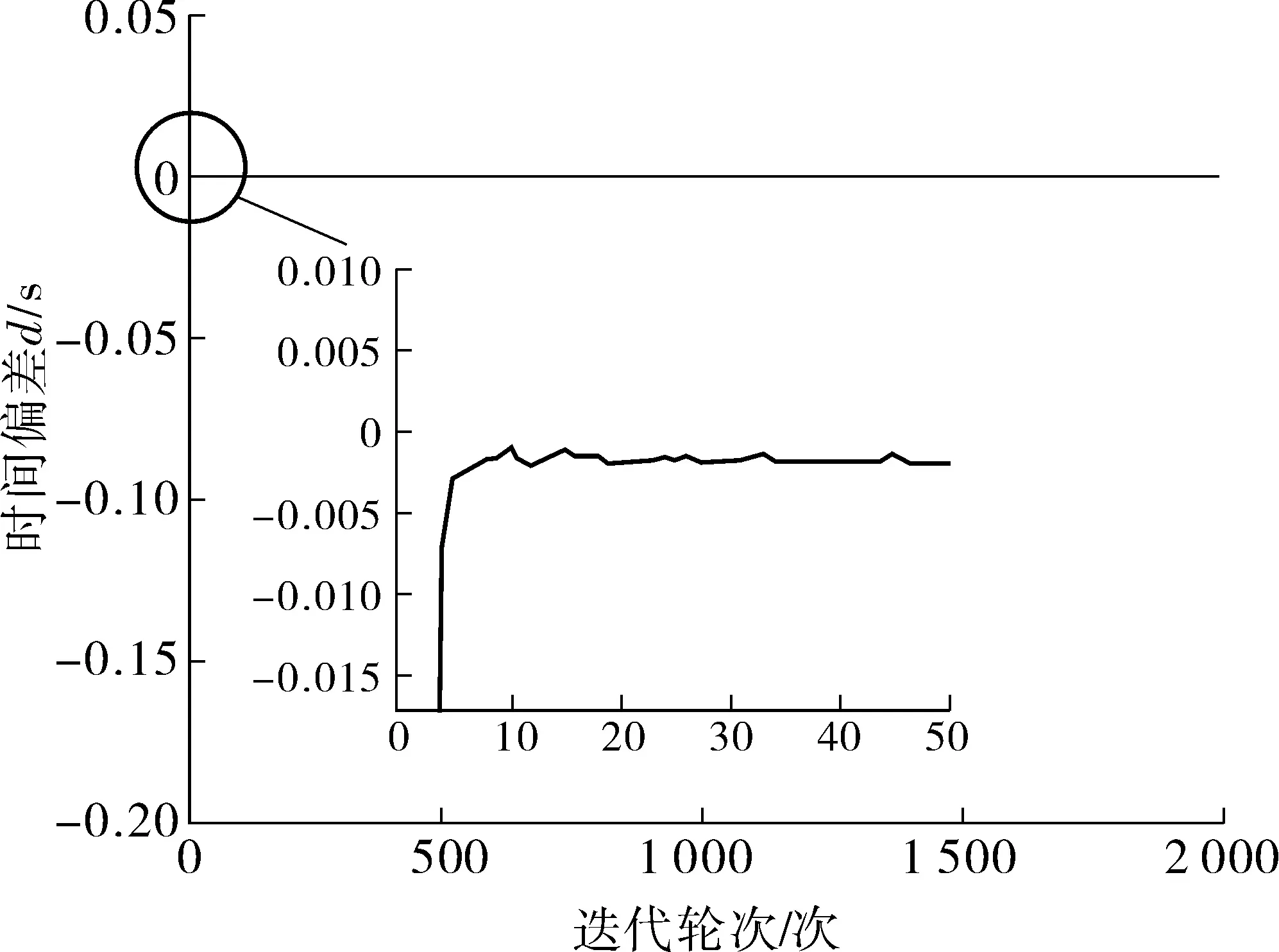
圖5 兩節點使用改變權重系數ρη的ATS算法在非對稱時延下進行2 000次通信后的時間差值Fig. 5 The time difference between two nodes using the ATS algorithmwith the changed weight coefficient ρη communicating 2 000 times withasymmetric delay

從圖5可發現：在對權重系數ρη修改后，使用ATS算法使得原本發散的狀況變成了收斂，但不同于無非對稱的時延的狀況。在無非對稱時延狀況下，兩節點間使用ATS算法在實現同步后，后續在時間偏差上沒有產生幅值變化。以本次仿真為例，在第9輪將時間偏差控制在0.001 5 s后，直至2 000個迭代輪次里一直維持在這個數值，而在圖5中存在非對稱時延的狀況下，從最終穩定時間偏差數值0.001 45 s來看，兩節點間不僅同步所需輪次變多，在第49次迭代才近乎平穩，且后續同步中依舊存在部分幅值波動，幅值波動在0.000 1 s以內。

4.3 多點通信ATS算法驗證

所描述系統為四輪獨立轉向系統，故選取多節點通信中任意5個節點進行ATS算法同步模擬。參照兩節間時間同步指標，有多節點時間偏差d′、多節點時間均值R′和多節點參考時間偏差方差D′。

4.3.1 定義4

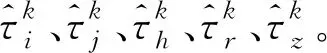
(16)

式中：x,y∈{i,j,h,r,z}，且x≠y。

4.3.2 定義5

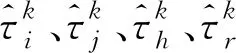
(17)

4.3.3 定義6

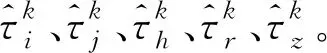
(18)

根據上述定義對模型進行仿真，橫坐標代表迭代次數，即絕對時間t。圖6和圖7(a)縱坐標表示5個節點時間偏差d′，單位：s；圖7(b)縱坐標表示多節點時間偏差均值R′，單位：s；圖7(c)縱坐標代表多節點參考時間偏差方差D′，單位：s2。分別設置5個初始偏移量不同、漂移斜率不同節點，具體參數為：ni本地時間漂移速度αi=0.999 9，初始漂移量βi=0.1；nj的本地時間漂移速度αj=1，初始偏移量βj=0.2；nh本地時間漂移速度αh=1.000 1，初始偏移量βh=0.3；nr本地時間漂移速度αr=0.999 8，初始偏移量βr=0.4；nz本地時間漂移速度αz=0.999 7，初始偏移量βz=0.5。

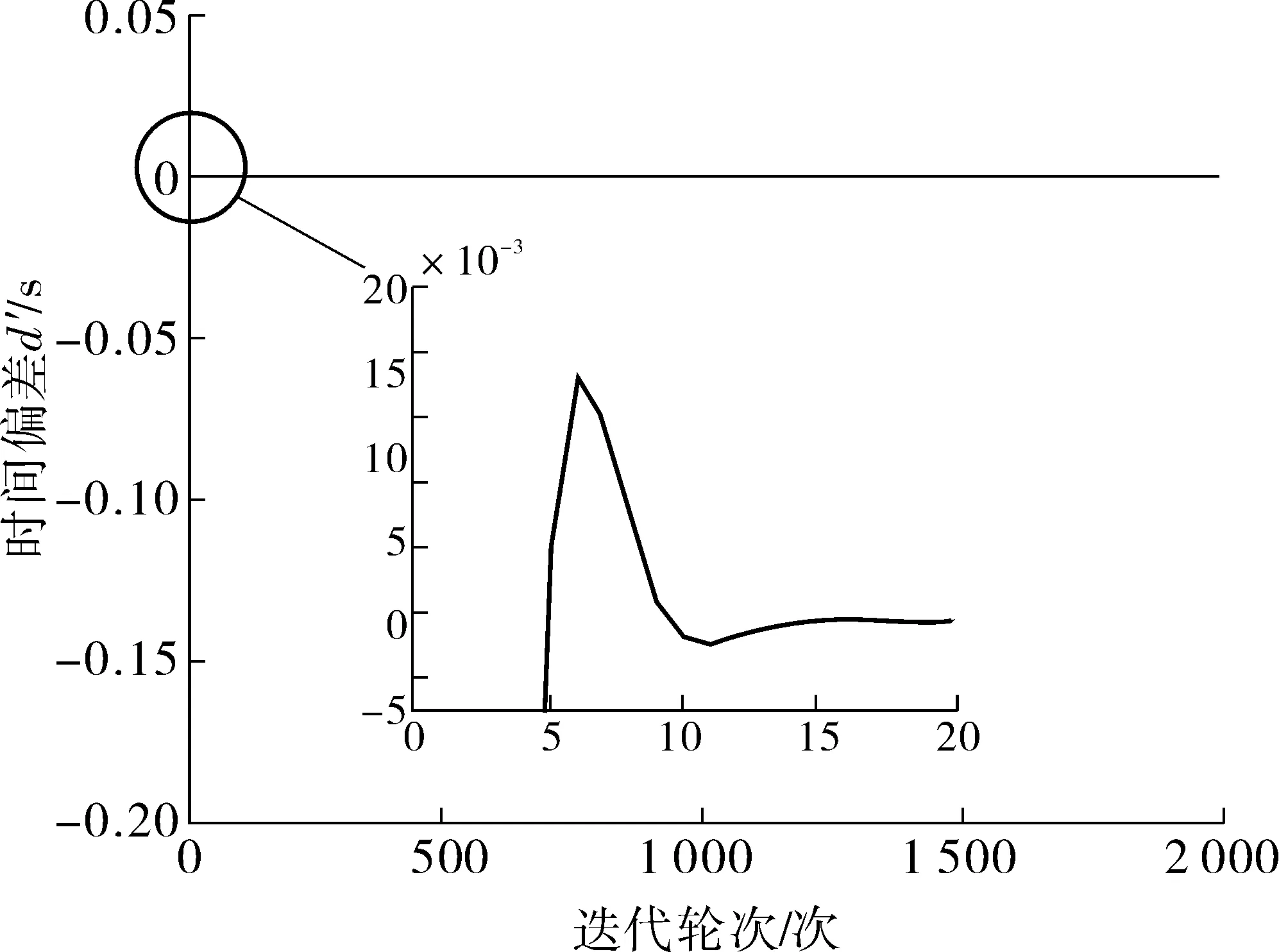
圖6 5個節點在沒有非對稱延遲下使用ATS算法進行2 000次通信后的時間差值Fig. 6 The time difference between five nodes using the ATSalgorithm for communicating 2 000 times without asymmetric delay

從仿真結果來看：5個節點的情況較2個節點發散幅度不盡相同。圖6在不存在非對稱延遲情況下，5個節點在第38次迭代的時間偏差d′趨近收斂，達到0.00 319 986 s，而后續通過算法依舊存在較小的偏差波動，其分別第43、319、591、1 137、1 409、1 682、1 955次時有了10-9s的時間偏差調整，整體較兩節點間同步迭代，在趨近收斂所需輪次上多進行了34輪的通信。在存在非對稱通信延時〔圖7(a)〕情況下，多個節點之間同樣存在估計時間偏差越來越大情況，當跌倒進行到第1 832次輪次時，5個節點間的時間偏差達到了5.068 s。

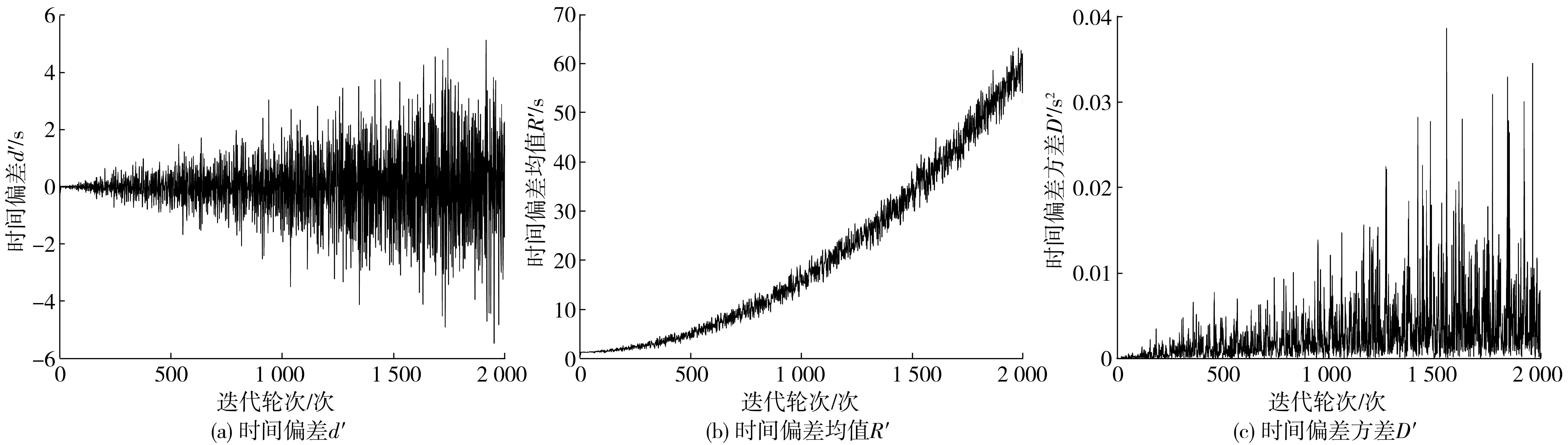
圖7 5個節點在ATS算法下進行2 000次通信的數值Fig. 7 The value of the five nodes communicating 2 000 times under the ATS algorithm

另外將圖7(a)與圖4(a)發散狀況合并，與圖8進行對比可知：整體而言，5個節點發散幅度小于2個節點，考慮到節點數量變多，根據時間偏差d′的定義，推測這可能是由于節點間估計時間差值有正負之分，在計算過程中相互抵消緣故。

5個節點使用ATS算法進行同步情況下，平均每個節點與真實時鐘偏差與2個節點情況相似，同樣呈震蕩形式增加，且發散幅值不斷擴大。以圖7(b)為例，在迭代第1 990～2 000次之間時，震蕩幅值最大，達到2.9 s，而整體R′值變化在迭代第1 995次時達到最大，為65.2 s。

修改ρη值后的ATS算法同樣適用于多節點狀況。圖9反映了5個節點使用修改ρη值的ATS算法在存在非對稱時間延遲情況下的時間偏差狀況。相較于沒有延遲在第49次收斂情況，其收斂所需的輪次增多了。以本次仿真數據為例，在第500次才達到近乎收斂結果，此時時間偏差d=0.000 31 s，最終迭代在第2 000次時d收斂于0.000 317 s。

圖8 2個節點和5個節點在2 000次通信下的時間偏差和時間偏差均值Fig. 8 The time deviation and time deviation mean between two nodes and five nodes after communicating 2 000 times

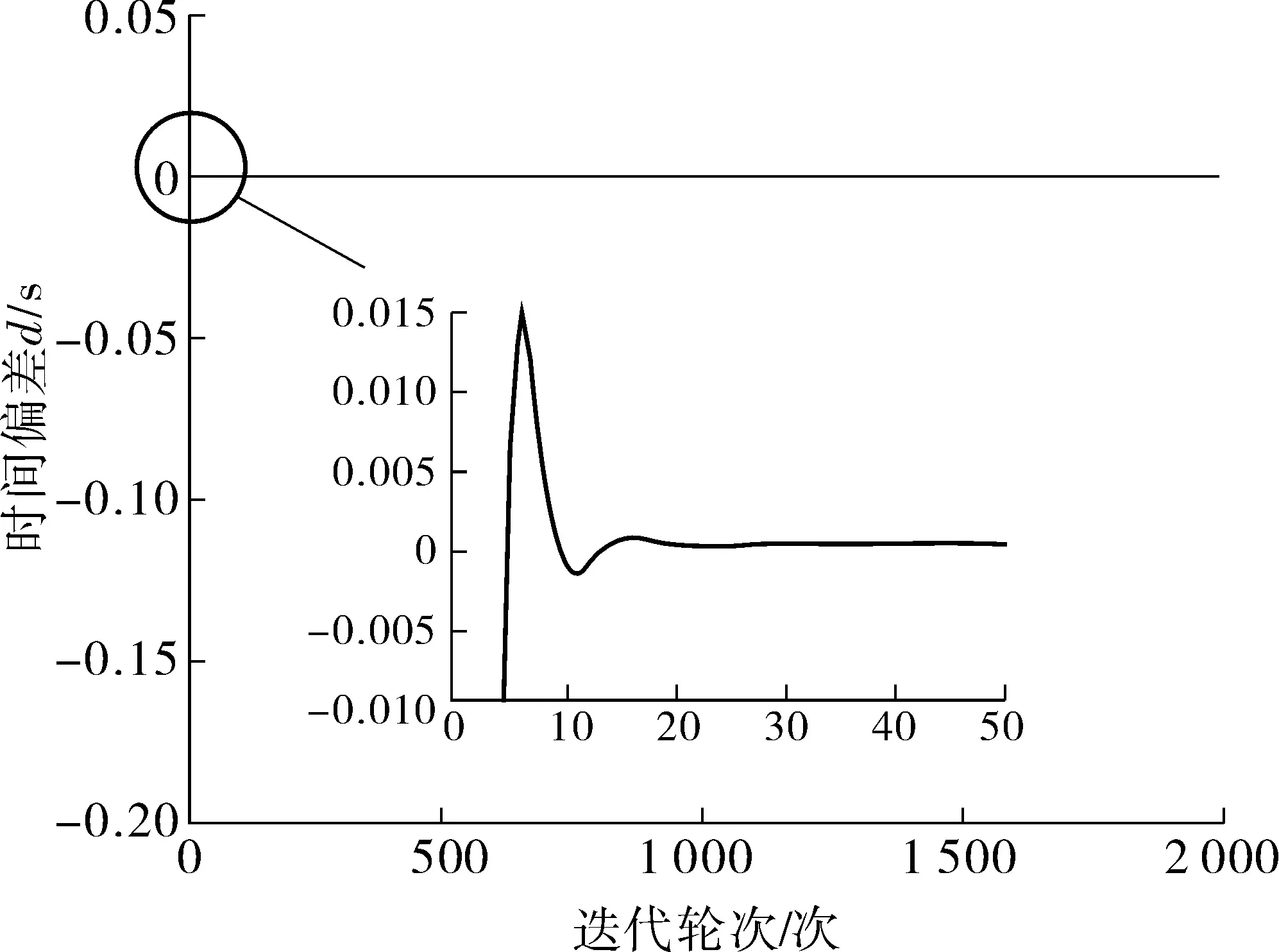
圖9 5個節點使用改變權重系數的ATS算法在非對稱時延下進行2 000次通信后的時間差值Fig. 9 The time difference between five nodes using the ATS algorithmwith the changed weight coefficient after communicating 2 000 timeswith asymmetric delay

5 結 語

筆者研究了對于存在通信延時情況下，ATS算法在車輛四輪獨立轉向中的運用狀況。證明了在存在非對稱有界通信延時情況下，多個節點無法在有限時間內將時間偏移速度和時間偏移量估計值控制于一個有界范圍內，這標志著ATS算法在存在非對稱通信時延的CAN網絡中無法實現時間同步。

為研究影響其發散狀況因素，筆者定義了時間偏差、時間偏差均值及時間偏差方差這3個指標，并在2個節點和5個節點狀況下分別進行仿真試驗，得出節點越多節點間時間發散越快的結論。對于擁有更多車輪車輛，對應于網絡中擁有更多節點狀態下，利用 ATS算法會呈現發散速度更快狀況，并在之后通過相關實車試驗驗證了該結論正確性。

此外，筆者分析了影響ATS算法發散的因素，并通過理論推導、仿真與實車試驗驗證了該方法的可行性，通過對發散因子修正實現ATS算法在四輪獨立轉向CAN網絡中的時鐘同步。目前ATS時間同步算法不適用于四輪獨立轉向，且隨著車輛輪數增多，其時間發散速度也越快，但經過對ATS算法中相關權重系數修改可實現在四輪獨立轉向中的時間同步。