基于響應曲面法風電齒輪箱行星架拓撲優化設計 *
雷 林,丁明澤,胡洪偉,張 敏,侯怡鑫
(1. 重慶交通大學 航運與船舶工程學院,重慶 400074; 2. 中船重工(重慶)西南裝備研究院有限公司,重慶 401147)
0 引 言
風能作為一種清潔能源發展的新趨勢,逐漸受到學者的關注。風電齒輪箱是風力發電領域的重要設備,均采用行星傳動,是典型的低速、重載、變轉矩和增速傳動。
在齒輪箱的故障率中,行星傳動相關的故障率約占40%[1]。行星架結構設計及性能參數直接影響風電齒輪箱的傳動效率和效果。行星傳動簡圖如圖1(a)[2],行星架三維模型如圖1(b)。
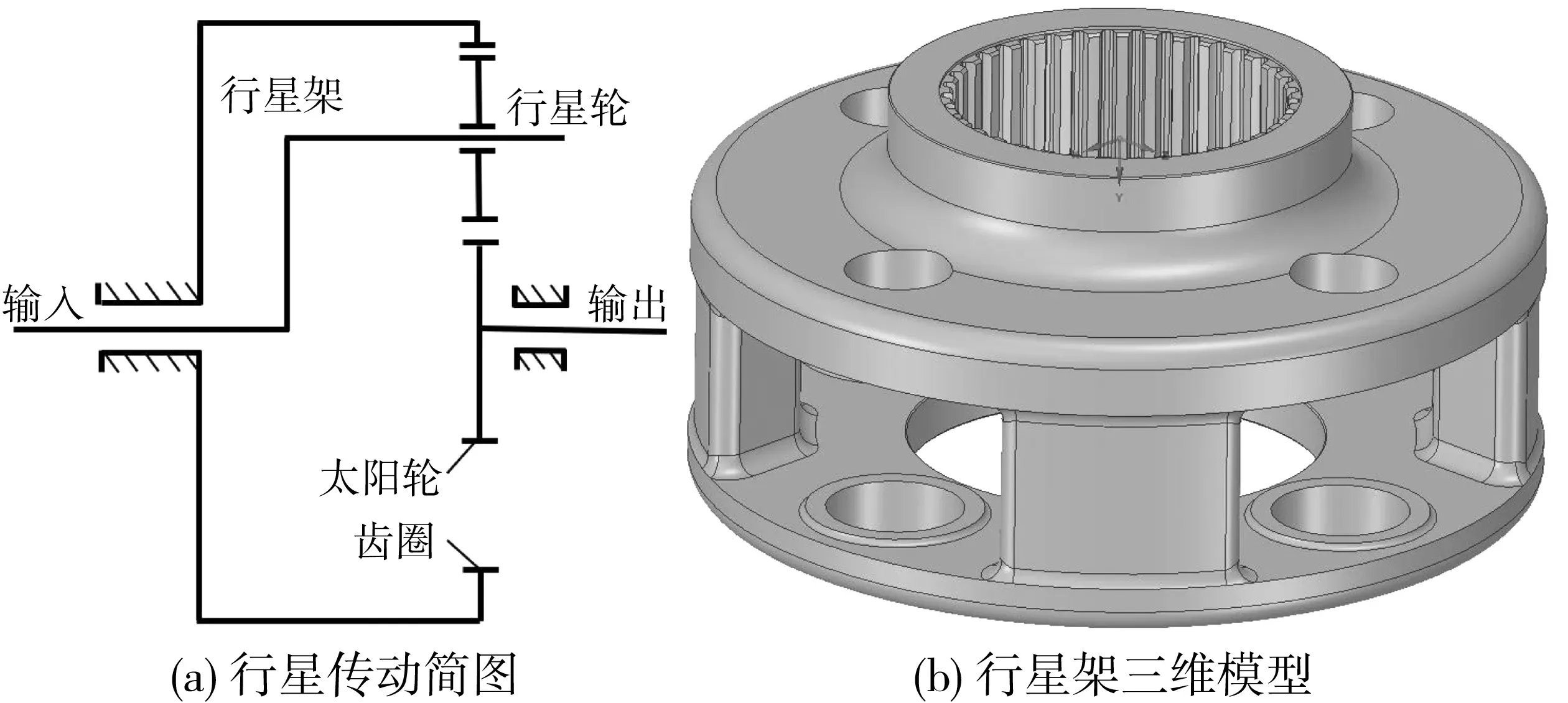
圖1 行星架工作原理及結構Fig. 1 Working principle and structure of planet carrier
此外S.SANKAR等[11]、YI Pengxing等[12,15]、D. M. BLUNT等[13]、HAO Dongsheng等[14]分別就風力發電機齒輪箱軸承失效形式、多目標性能提高、檢測其疲勞裂紋方法、行星齒輪架和軸組件的過盈配合和模態特性等方面展開相應研究。
上述學者針對風電齒輪箱行星架進行拓撲優化的過程當中,均以某一個或某幾個指標作為優化目標,并未考慮風電齒輪箱行星架的綜合結構性能展開分析與優化。因此筆者結合呼斯樂圖等[9]、楊龍[10]對其他不同應用領域的行星架研究成果,以結構輕量化及提高結構性能為目標進行綜合考量,對某型號風電齒輪箱行星架展開拓撲優化設計。
根據GB/T 19073—2018《風電發電機組齒輪箱設計要求》,應依據第四強度理論(Von Mises應力)評估行星架靜態承載性能。根據有限元分析結果,采用基于響應曲面法的拓撲優化遺傳算法,以行星架自重、形變量及Von Mises應力值作為優化目標,針對行星架進行尺寸優化設計,最終獲得該型號行星架結構最佳方案。
1 行星架有限元前處理
1.1 行星架材料參數
筆者所分析的風電齒輪箱行星架材料參數如表1。

表1 行星架材料參數Table 1 Material parameters of planetary carrier
1.2 行星架模型簡化
對行星架幾何模型進行適當簡化,將花鍵部位進行光滑處理,在保證對結構強度和變形形變影響較小的前提下,避免細微結構引起的網格畸形,簡化后行星架三維模型如圖2。
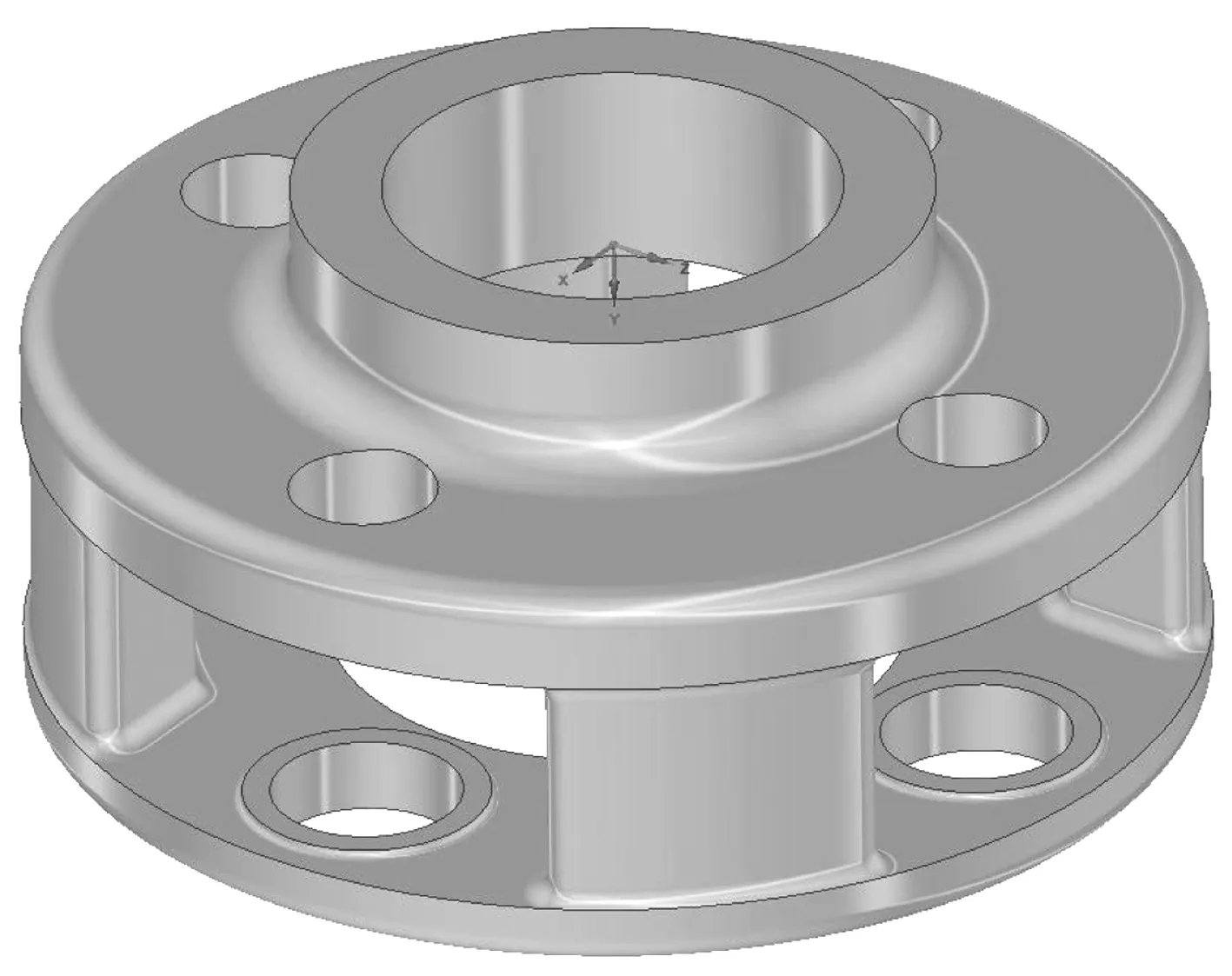
圖2 行星架簡化三維模型Fig. 2 Simplified three-dimensional model of planetary carrier
1.3 邊界條件及載荷施加
對單獨風電齒輪箱行星架進行有限元分析時,在4個行星輪軸孔處施加反向轉矩。反向轉矩總和等于輸入轉矩,載荷類型為面載荷[2],轉矩為 46 240 N·m。加載方式如圖3中B、C、D和E。
2.2.4 混播比例對混播植物Pro含量的影響 不同混播比例對禾草Pro含量均無顯著影響(表3),而對苜蓿Pro含量有明顯影響(表4)。B1處理Pro含量最高,比B2,B3和B4處理高24.48%,27.41%和49.50%,差異極顯著(P<0.01);單播苜蓿苜蓿Pro含量分別比B3和B4處理高17.77%(P<0.05)和38.19%(P<0.01),B2處理Pro含量比B4處理高20.10%(P<0.05),其余處理間苜蓿Pro含量無顯著差異(P>0.05)。
行星架端面施加完全固定約束,如圖3中A;考慮圓柱滾子軸承支承作用,在左右兩側圓柱面上施加徑向約束,如圖3中F和G[8]。
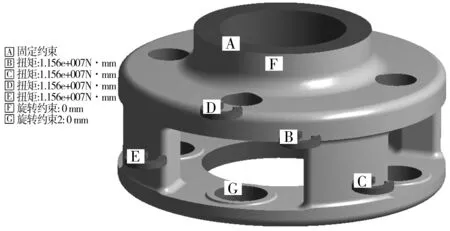
圖3 邊界條件及載荷施加Fig. 3 Boundary conditions and load application diagram
1.4 網格無關性驗證
對風電齒輪箱行星架進行有限元網格劃分,全局使用六面體網格,尺寸設置為6 mm。為研究網格特性,局部使用不同尺寸的面網格進行加密,具體加密區域如圖4,最大Von Mises應力值變化趨勢如圖5。
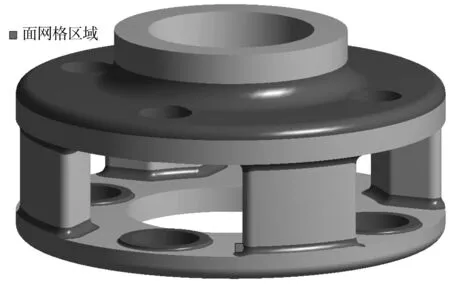
圖4 局部網格加密區域Fig. 4 Local grid encryption area
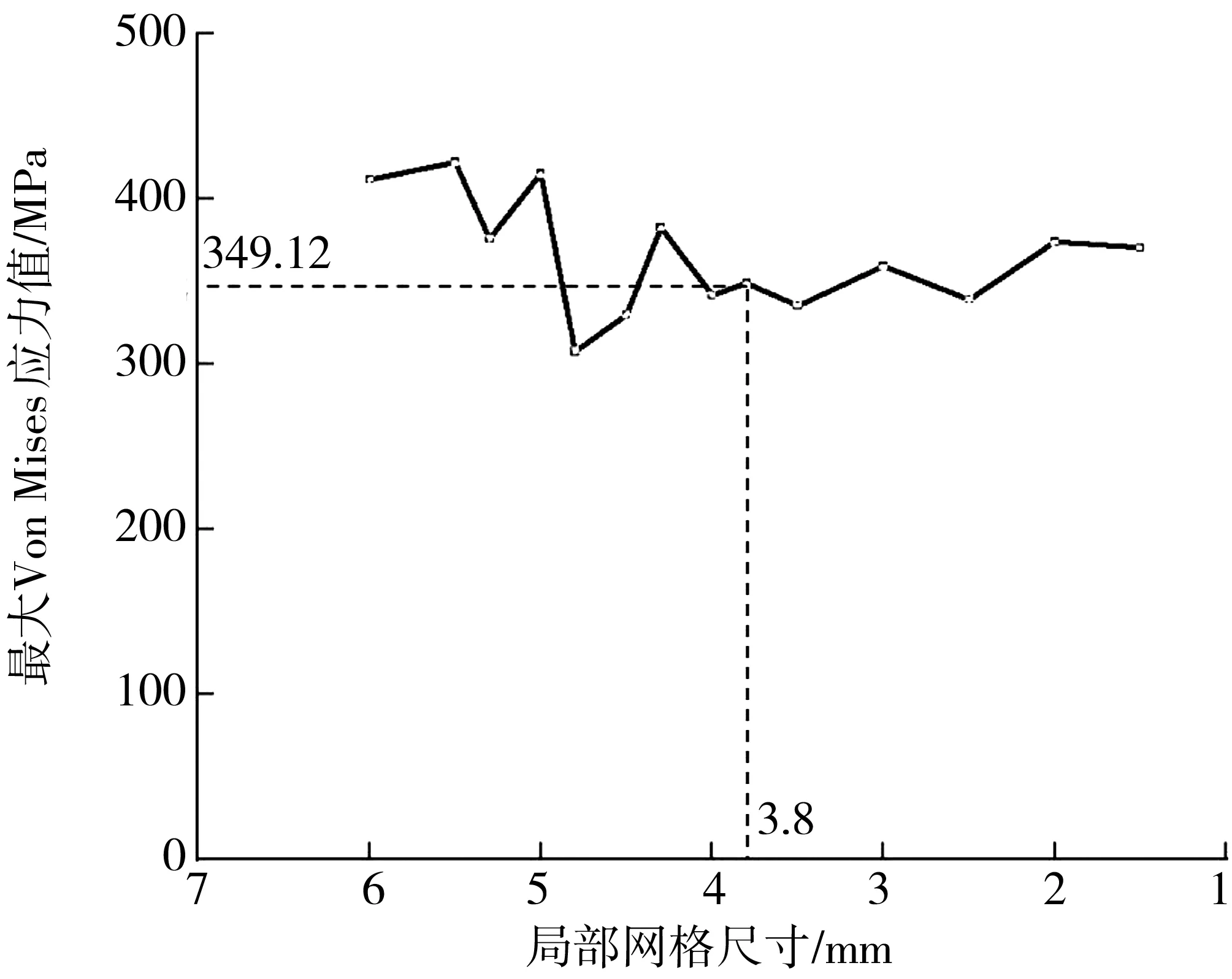
圖5 最大Von Mises應力走勢Fig. 5 Trend chart of maximum Von Mises stress
綜合權衡計算精度和成本,選擇應力變化幅度5% 作為網格無關性判據,以全局網格尺寸6 mm、局部網格尺寸3.8 mm作為最終網格劃分方案,總計55 236 個節點,71 788個單元。
2 行星架拓撲優化設計
2.1 優化設計數學模型
優化設計主要包括設計變量、目標函數以及約束條件。設計變量是優化設計中待確定的參數。目標函數是優化設計中用于判別設計方案優劣標準的數學表達式,常用F(X)表示,如式(1):
(1)
式中:μ為權重系數;xi為設計變量。其中,設計變量的個數確定了目標函數的維數,設計變量的冪及函數值確定了目標函數的性質。優化設計中尋求目標函數極值的某些限制條件,稱為約束條件。最優化問題的基本表達式通常如式(2)~式(5)[16]:
X={x1,x2,x3,…,xn}T(X≥0)
(2)
F(X)→min(或max) (X≥0)
(3)
hj(X)=0 (j=1,2,…,k;X≥0)
(4)
Gi(X)≤0 (i=1,2,…,n;X≥0)
(5)
式中:X為設計變量的集合;F(X)為目標函數;hj(X)、Gi(X)以及X≥0分別表示優化問題中該滿足的約束條件。
2.2 拓撲優化
2.2.1 響應曲面及靈敏度分析
利用響應曲面方法對風電齒輪箱行星架進行分析,首先要提取數個預估變量參數。根據張立勇[4]、東立劍[5]的研究,筆者初步選取輸入端面拉伸量x1、輸入端面環半徑x2、輸入端面四銷軸孔半徑x3和軸肩倒角半徑x4為預估變量參數,其中輸入端面拉伸量即決定輸入端面厚度D1(圖6),同時確定預估變量參數及設置變量參數范圍,各變量參數初始值及所取變量參數范圍如表2。
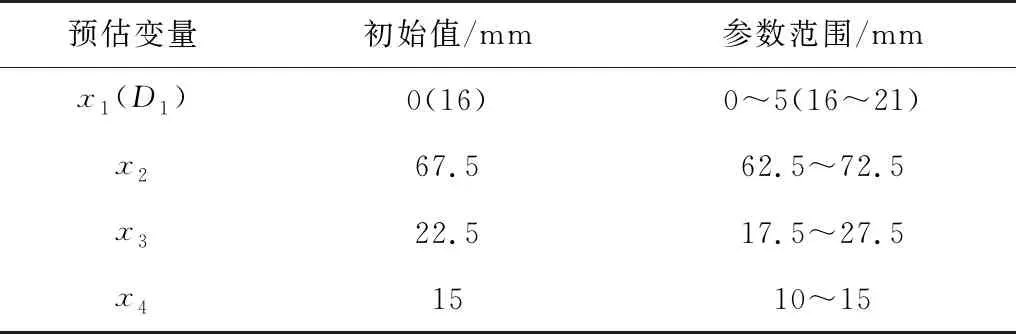
表2 預估變量參數值Table 2 Estimated variable parameter value
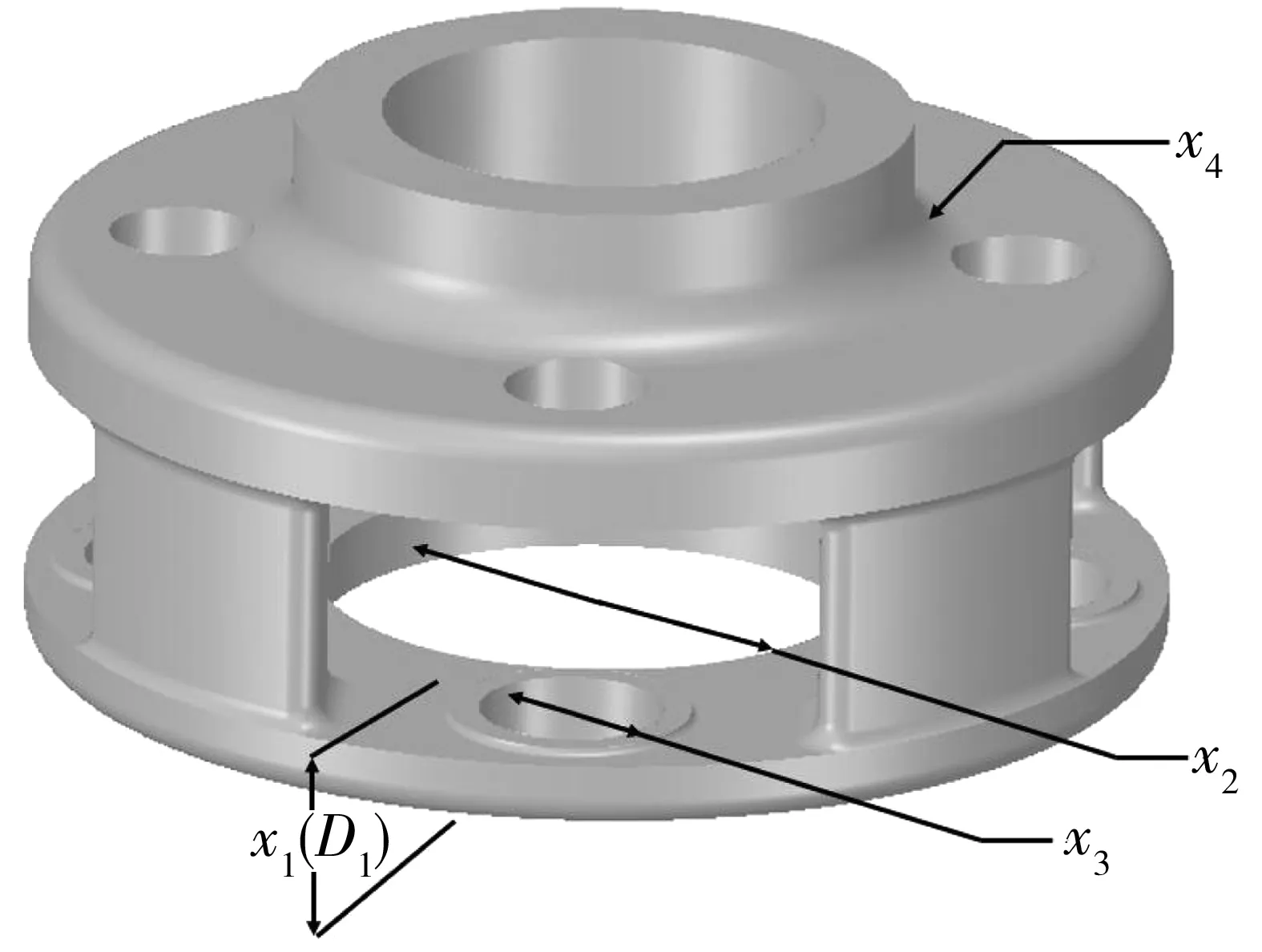
圖6 預估變量參數Fig. 6 Estimated variable parameters
筆者以降低風電齒輪箱行星架自重、最大Von Mises應力值及最大形變量作為優化目標,基于Workbench平臺,利用響應曲面法進行計算求解,可以得到25組符合范圍要求的不同變量參數數值及其所對應的優化目標值,即行星架自重、最大Von Mises應力值和最大形變量值,其中:F1(X)為行星架自重;F2(X)為行星架最大Von Mises應力值;F3(X)為行星架最大形變量。
由數據統計結果可得各優化目標響應曲面,如圖7。行星架自重響應曲面代表預估變量x1、x2、x3和x4與行星架自重之間的關系。分析圖7(a)可知,隨x1和x4增加,行星架自重增大;隨x2和x3增加,行星架自重減小。
行星架最大Von Mises應力值響應曲面代表預估變量與行星架最大Von Mises應力值之間的關系。分析圖7(b)可知,隨x1、x4增加,最大Von Mises應力值減小;隨x2、x3增加,最大Von Mises應力值增加。
行星架最大形變量響應曲面代表預估變量與行星架最大形變量之間的關系。分析圖7(c)可知,隨x3增加,最大形變量增大;隨x1、x4增加,最大形變量減小;x3對最大形變量影響較小。
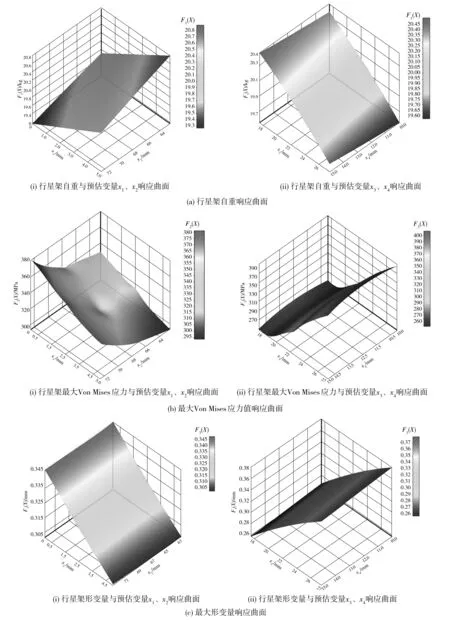
圖7 各優化目標響應曲面Fig. 7 Response surface of each optimization target
對綜合響應面模型進行分析可知,所選參數之間的組合對行星架的自重、最大形變量和最大Von Mises應力起著重要的作用。單一因素的改變不能從整體上改變行星架的性能,需要對輸入參數進行有效組合,才能合理優化行星架的性能[5]。
靈敏度分析是對模型參數的動態變化過程(即瞬時變化過程)進行分析,研究特定參數對模型性能的影響情況[8]。針對筆者所研究的風電齒輪箱行星架,對于自重、最大Von Mises應力值和最大形變量,各預估變量參數的靈敏度如圖8。
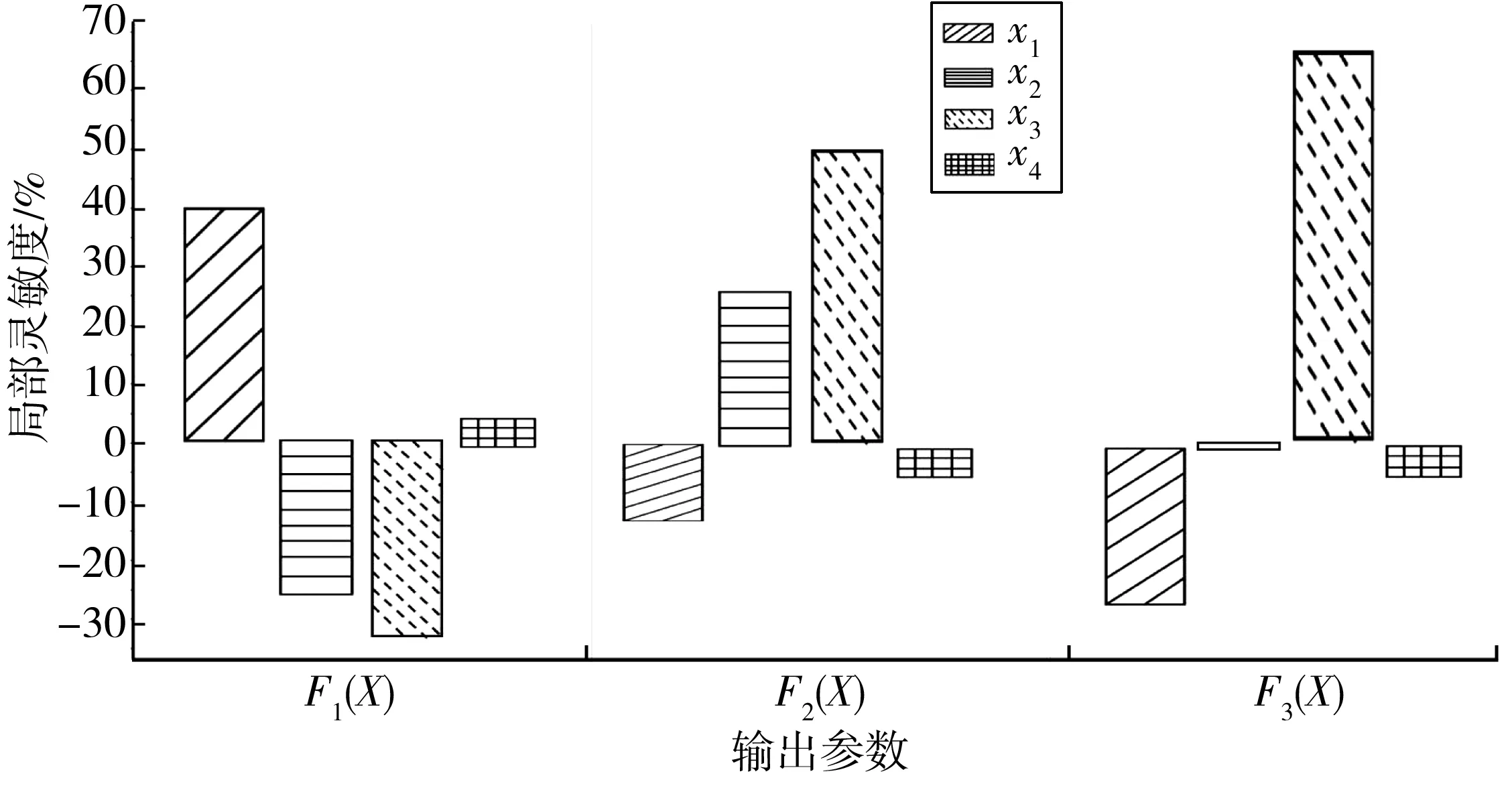
圖8 各變量靈敏度Fig. 8 Sensitivity relationship of each variable
根據所得響應曲面及靈敏度結果,各變量參數與優化目標之間的關系如表3。
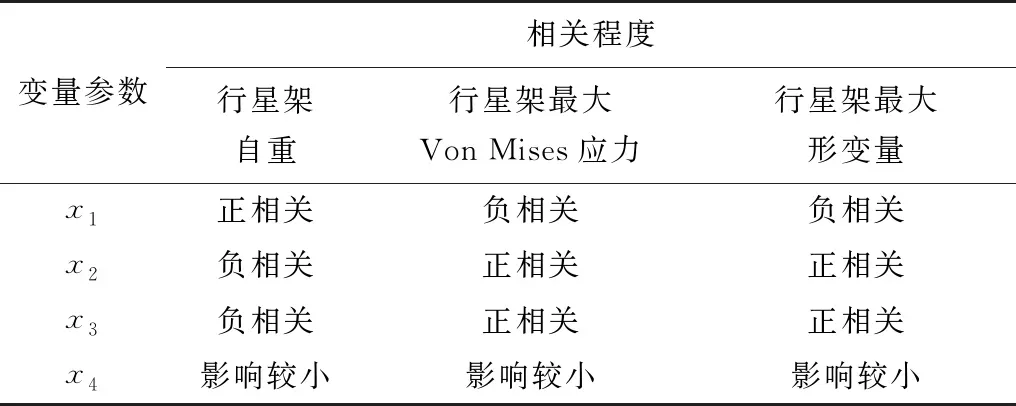
表3 各變量參數與優化目標之間的關系Table 3 Relationship between various variable parameters andoptimization objectives
2.2.2 尺寸優化設計
通過各預估變量響應曲面分析及靈敏度分析,可以進行優化變量提取,最終確定x1、x2、x3為優化方案變量,修正優化方案變量參數范圍,如表4。
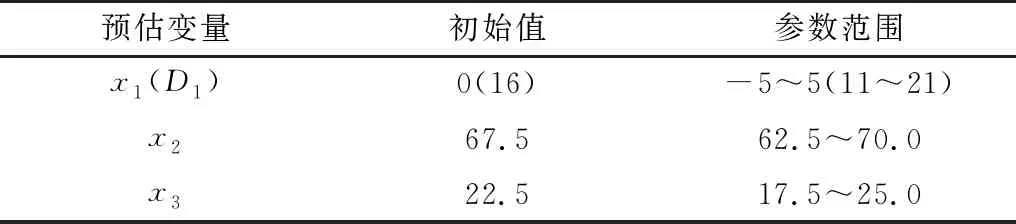
表4 優化方案變量參數值Table 4 Variable parameter value of optimization scheme mm
根據優化變量參數及參數范圍展開尺寸優化設計。綜合考慮計算資源及樣本可靠性,提取100組優化設計方案,成功優化方案99組,并基于優化目標(行星架自重、最大Von Mises應力值和最大形變量)進行排列組合,選取最優解,最終獲得3組最佳優化方案,如表5。
2.3 結構優化前后性能分析
綜合考慮優化設計方案,以風電齒輪箱行星架結構輕量化作為衡量標準,選取表5中優化方案2作為優化設計方案。行星架結構優化前Von Mises應力分布及形變分布如圖9;行星架結構優化后Von Mises應力分布及形變分布如圖10。
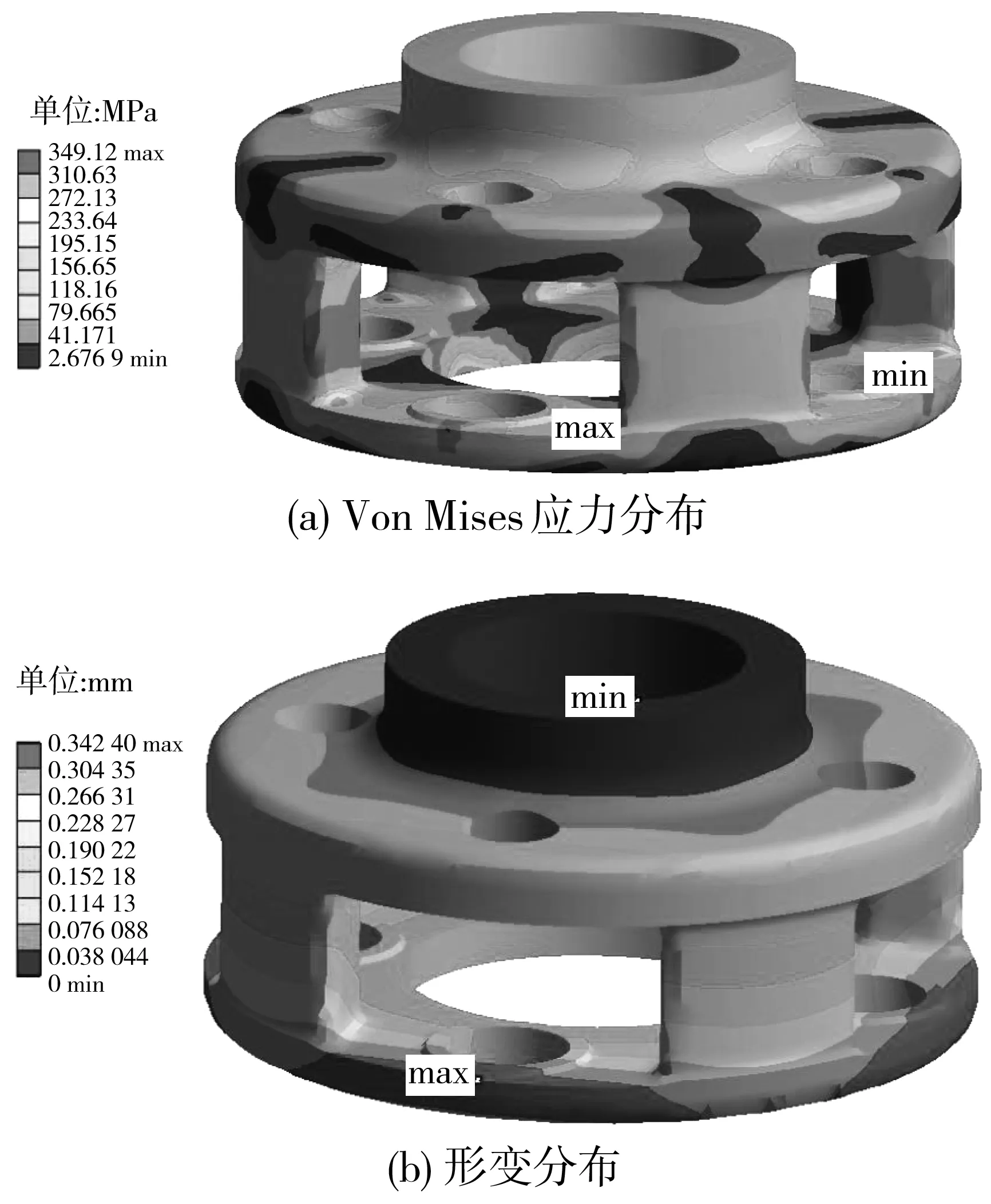
圖9 優化前行星架Von Mises應力及形變分布Fig. 9 Distribution of Von Mises stress and deformation of theplanet carrier before the optimization
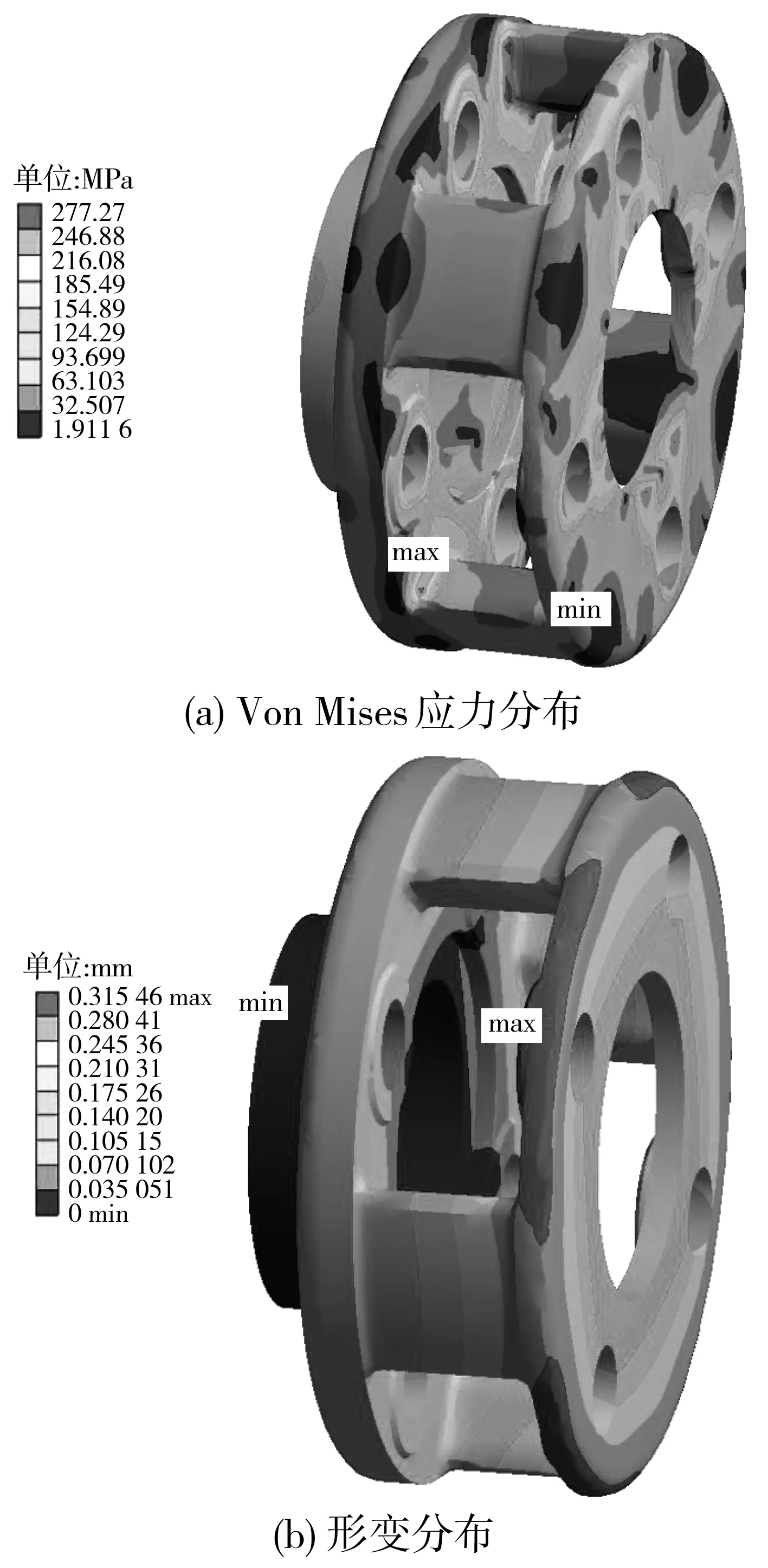
圖10 優化后行星架Von Mises應力及形變分布Fig. 10 Distribution of Von Mises stress and deformation of theoptimized planet carrier
優化方案2下,優化前后數據對比如表6。
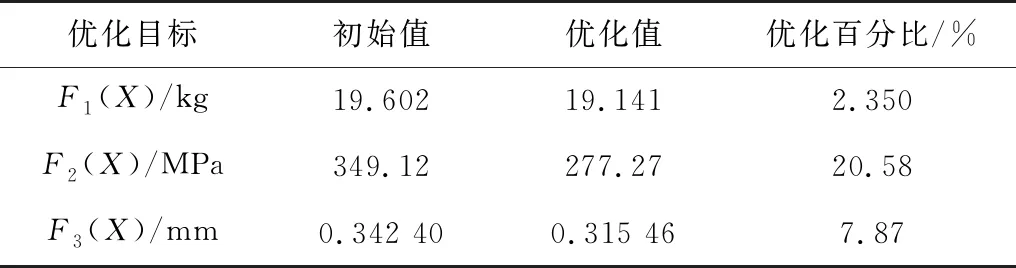
表6 優化前后數據對比Table 6 Data comparison before and after optimization
3 結 語
筆者建立某型號風電齒輪箱行星架三維模型,開展有限元分析,基于響應曲面法,以結構輕量化、減小最大Von Mises應力值及降低最大形變量作為優化目標,將行星架輸入端面拉伸量x1、輸入端面環半徑x2和輸入端面四銷軸孔半徑x3作為優化過程中的關鍵影響因素,并分析設計變量與優化目標之間的關系,從而進行拓撲優化。
根據99種優化方案,最終基于優化目標進行綜合考慮,選取該型號風電齒輪箱行星架結構的最佳優化方案。結果表明,行星架自重降低2.35%,最大Von Mises應力值降低20.58%,形變量降低7.87%,充分提高了該型號行星架綜合性能。為了更好地提高性能參數,可進行疲勞分析及實驗,展開進一步優化。

