Matlab在面向“拔尖學生”的大學物理教學中的應用*

師玉榮 顧永建 李 春

(中國海洋大學物理與光電工程學院 山東 青島 266100)

培養基礎學科拔尖人才是高等教育強國建設的重大戰略任務，拔尖人才培養計劃實施以來，培養了大批優秀人才.中國海洋大學在“基礎學科拔尖學生培養計劃2.0”背景下，結合學校海洋特色優勢成立了創新拔尖學生培養基地——崇本學院，崇本學院的學生是全校層層選拔出來的，他們的理論基礎知識扎實，知識接受能力強，有強烈的求知欲.面向“拔尖學生”的大學物理教學進行了一系列的教學改革，更加注重加強培養學生的實踐創新能力、解決實際問題能力和團隊協作能力，其中在教學中融入Matlab編程解決復雜物理問題的教學實踐取得了很好的教學效果.

1 課題的提出

隨著計算機技術的發展，數值計算已經成為一種重要的研究手段，其中Matlab軟件被稱為演算紙式的計算機語言，它簡單易學、容易入門，所以很快被作為教學輔助手段引入到很多學科教學中.在大學物理教學中最常見的Matlab的應用，大多是可以直觀動態地演示一些物理過程，如波動中的干涉、駐波、李薩如圖形等[1，2].

大學物理教學內容中有許多難點問題很難求解，或者不能求出解析解，例如力學中的“最速降線”問題，轉動參考系中受離心力和科里奧利力作用的質點的運動和衛星橢圓軌道等問題，它們的動力學微分方程是很難求解或者求解不出來的.如何處理這些問題，被譽為“科學怪才、教育楷模”的諾貝爾物理學獎獲得者費恩曼在他的普通物理教學中，曾這樣處理行星的橢圓軌道問題，他認為從更基本的動力學方程(即牛頓第二定律與萬有引力定律相結合)出發，用盡可能少的知識獲得行星繞日運行的軌跡，由于在普物階段，尚無法探討非線性微分方程的理論解，那么數值差分迭代求解微分方程就成為不二選擇[3,4].筆者在教學過程中為了提高教學效果，應用Matlab編程解決過“最速降線”的相關問題[5]，也模擬過轉動參考系中質點的運動問題和行星的橢圓軌道問題.在課堂上動態演示這些程序的運算結果，形象直觀，有助于學生對物理知識的理解.

基于教學實踐筆者認為“拔尖學生”有能力應用Matlab編程解決如上的問題，讓學生親歷這個編程過程，不但可以加深他們對這些物理難點問題的理解和微積分的應用，而且可以在這個過程中培養學生的自主學習能力、解決實際問題的能力.

2 Matlab編程解決力學問題的教學設計流程

教學設計采用教師引導，助教指導，學生小組協作學習的形式.我們挑選了有豐富Matlab編程經驗，且物理理論功底深厚的助教，助教協助學生安裝軟件，檢查點評學生小組作業，輔導答疑學生編程過程中遇到的難題.每項任務需要小組協作完成，6～7人組成一個小組，組員相互借鑒，取長補短促進學習，培養學生團隊協作精神.考慮到有一部分學生沒有接觸過Matlab編程，教學設計流程是由淺入深、層層遞進的，在力學課程中結合內容進度設計了幾個案例，從最速降線→螞蟻追逐→轉動參考系中質點的運動→衛星軌道，引導學生從入門→初步應用→逐步深入解決復雜動力學問題，從簡單到逐步復雜，前兩個簡單案例各用一周的時間，后面復雜案例分別用兩周或三周的時間.

第一個案例最速降線問題是質點運動學一個經典問題，學生對最速降線的實驗現象非常驚奇，但是當學生試圖應用學過的物理知識求解時，發現即使最簡單的圓弧路徑上所用的時間也無法求解，但是Matlab程序，不但可以直觀動態地演示質點沿直線、拋物線、圓弧和旋輪線幾種不同曲線的軌道從相同起點到相同終點的過程的快慢順序，并且能計算出每個軌道所用的時間[3].程序語句簡單易懂，應用機械能守恒和瞬時速度的定義式，利用微積分思想把整個過程看成由許多微小的過程組成，每個微小過程視為勻速直線運動，通過Matlab強大的計算功能，計算出每個無窮小過程的時間，求和(積分)得出整個過程所用時間，總之程序借助簡單的物理原理和微積分就解決了.通過向學生展示程序語句，拋磚引玉讓學生看到Matlab編程入門簡單，有信心可以學會，激發學生學習編程解決力學問題的興趣.

第二個案例是獵人打猴，是質點運動中非常有趣的例子，子彈瞄準猴子，子彈打出的同時，猴子自由落體，不管子彈速度多大，總能打中猴子.原理簡單，學生通過簡單的語句即可模擬子彈總是能打中猴子的動態過程，讓學生初步體會到編程的成就感，增強信心.

第三個案例是“螞蟻追逐”問題，3只螞蟻分別處于等邊三角形的頂點，每只螞蟻總是以另一只螞蟻為目標以相同的恒定速率追逐，求3只螞蟻相遇所用的時間和走過的軌跡方程.這個案例要求學生應用極坐標的速度定義式結合微積分解決，畫出螞蟻的動態軌跡以及計算出所用時間，通過這個案例學生可以加深對極坐標系的認識并能熟練應用.

第四個案例是勻速轉動的光滑圓盤上的質點在離心力和科里奧利力作用下的運動軌跡問題.轉動參考系中質點的動力學問題對學生來說是難點，具有極大的挑戰性，徑向和橫向的運動相互影響，在極坐標系中其徑向和橫向的動力學方程分別為

式中的ωp為圓盤的轉動角速度，vr和vθ分別為徑向速度和橫向速度，這個動力學方程無法給出解析解，但是Matlab可以給出數值解.這個案例要求學生列出極坐標系中的動力學方程，在助教的協助下編程畫出不同初速度條件的軌跡方程，學生通過這個案例不但可以更深入地理解轉動參考系中質點的運動，而且進一步掌握了如何處理極坐標系中的動力學方程.

第五個案例讓學生自主解決地球衛星橢圓軌道的問題.關于行星軌道求解的研究，基于開普勒運動的角動量守恒和萬有引力場中的機械能守恒，可以給出極坐標表示的圓錐曲線方程，這在《新概念物理教程力學》[6]一書中有詳細的推導.但是費恩曼的從基本定律出發求數值解的思路在大學物理的教學中更有效.我們要求學生在自己建立模型的基礎上，一要計算近地圓形軌道的周期并與理論對比，二是畫出給定高度和速度的衛星的橢圓軌道.

總之通過在教學過程中制定有序計劃，通過簡單實例引導學生入門，引起學生興趣，再通過解決越來越復雜的問題，最終讓學生可以自主解決教學過程中遇到的不能理論求解或難于求解的問題，培養學生解決實際問題的能力.

3 實踐教學成果

3.1 作業展示

下面展示幾個任務中學生成果選例.圖1是獵人打猴的運行動態圖截圖，可以展示子彈以不同的初速度瞄準射擊猴子，總是擊中目標，初速度小的在更低的位置射中猴子.圖2是3只螞蟻追逐問題的動圖截圖，動圖可以顯示任何時刻3只螞蟻都在一個等邊三角形的頂點上，等邊三角形旋轉著縮小到三角形的中心.圖3顯示了勻角速轉動光滑的水平圓盤上，一個質點由相對圓盤靜止開始，在離心力和科里奧利力的作用下的運動軌跡，改變參數還可以顯示不同初速度的運動情況.圖4顯示了在地球表面附近，以9.9×103m/s(大于第一宇宙速度)初速度發射的衛星的橢圓軌道，改變條件可以得出任意位置和初速度的衛星的軌道.

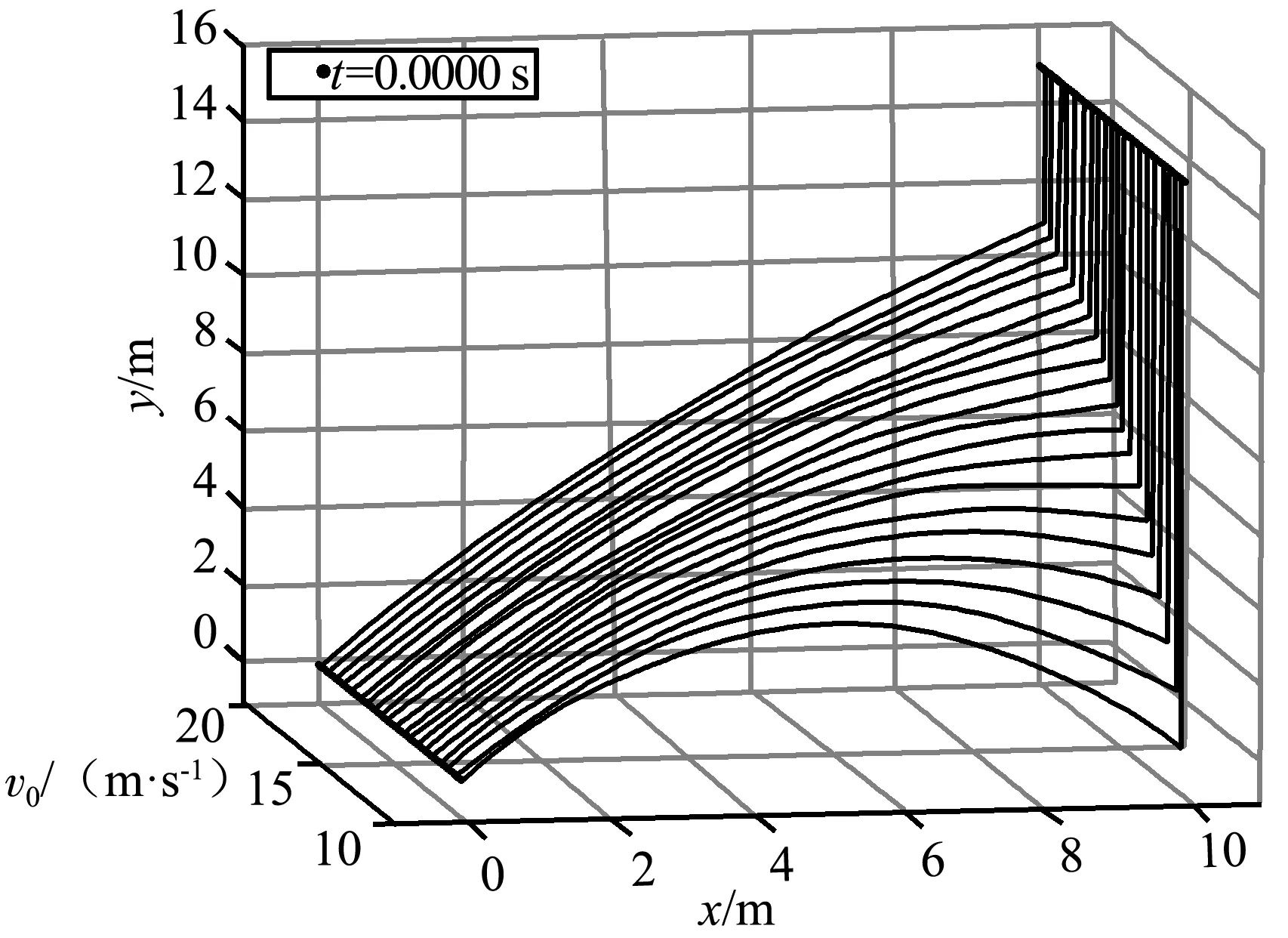
圖1 獵人打猴

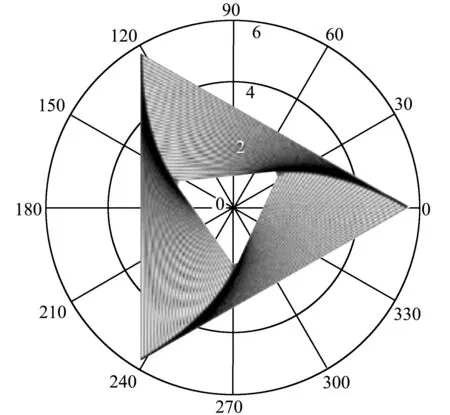
圖2 螞蟻追逐

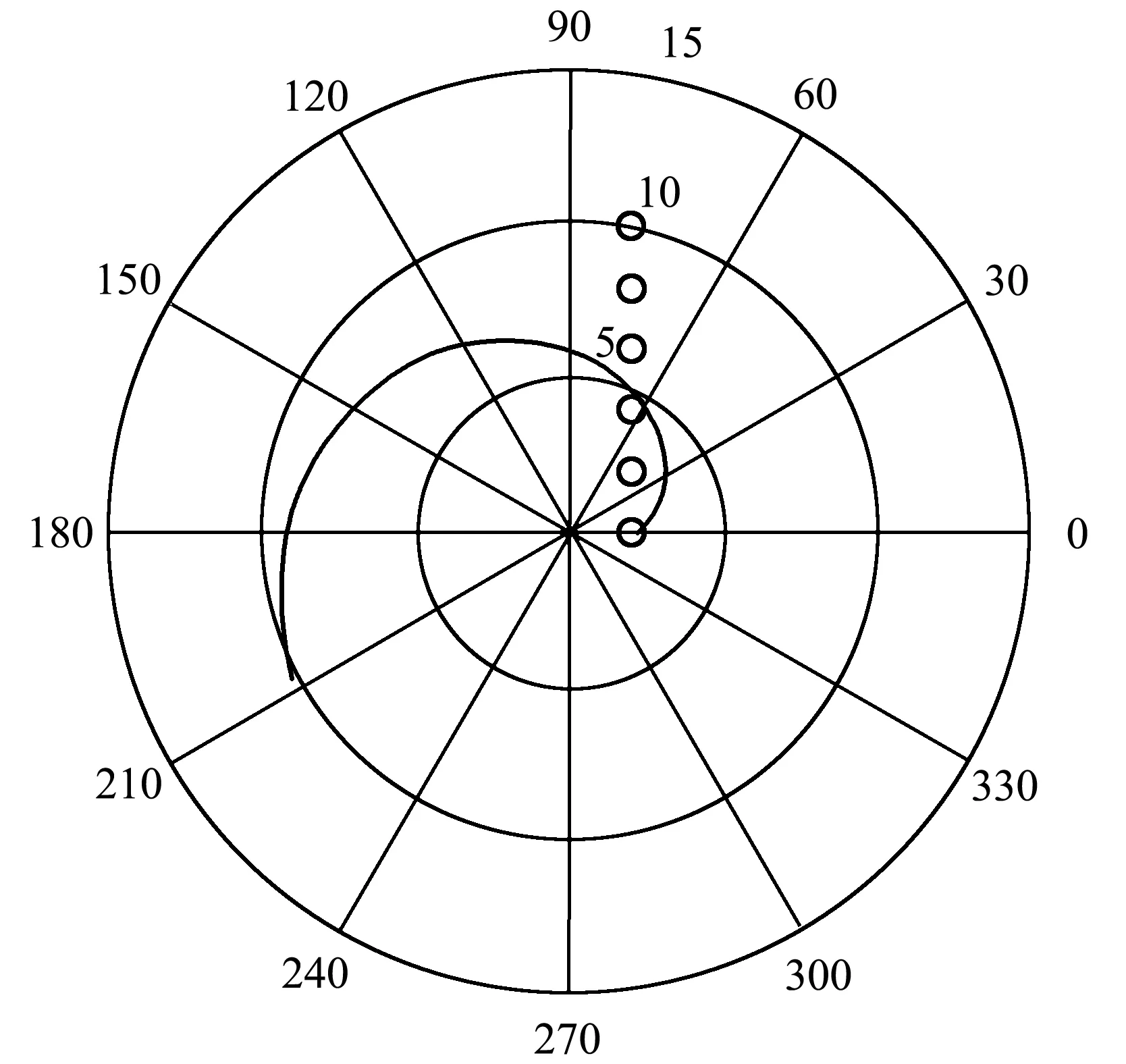
圖3 勻角速轉動圓盤上質點相對圓盤(實線)的軌跡和相對地面的軌跡(小圓圈)

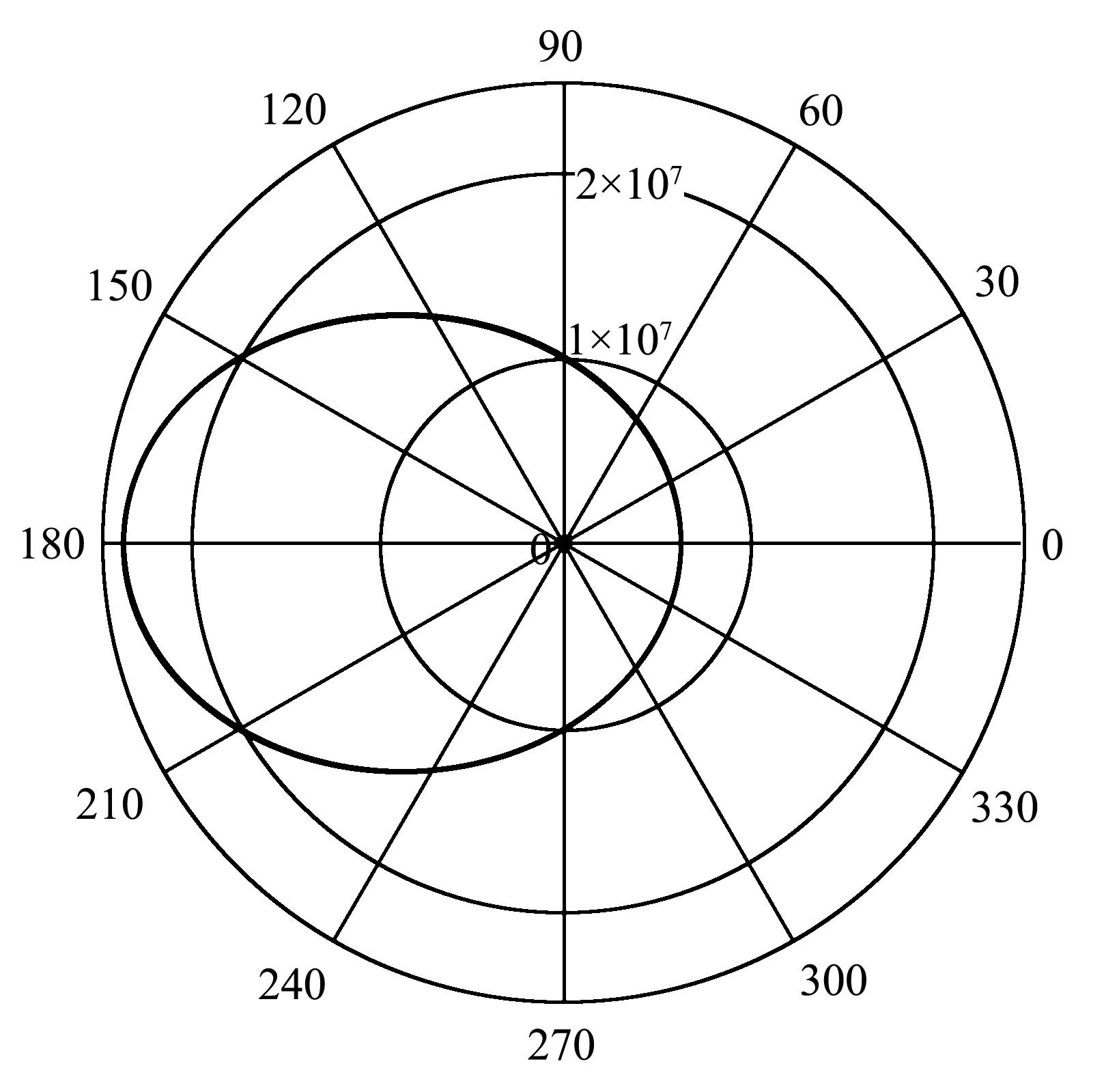
圖4 衛星橢圓軌道

3.2 后續學習影響

在后續學習中學生能自覺地運用Matlab編程解決問題，有學生解決了月亮相對太陽的軌道形狀問題，有學生描繪出了傅科擺在不同緯度、不同初始條件下的擺動平面的旋轉形狀問題；而且在后續學習中學生可以熟練應用極坐標系解決問題；這些表現說明了該教學設計加深了學生對物理知識的掌握深度，提高了學生解決實際問題的能力.

在大學物理的熱學部分學習中，這些“拔尖學生”成功地模擬了不同氣體的麥克斯韋速率分布曲線和傅里葉熱傳導的模擬問題，提高了熱學內容的教學效果.

4 教學效果及總結展望

學生在總結中提到這個基于Matlab解決力學問題的學習過程對他們有很大的挑戰性，對他們的學習幫助很大，他們更深刻理解了微積分的本質，更深刻理解了物理原理，一舉多得；而且對數值模擬經過無數步得出的結果與理論計算或者與實際觀測的結果一致，感覺神奇、震撼.總之學生認為這是從理論跳躍到解決實際問題的過程，提高了他們解決實際問題的能力，強烈建議力學教學保留這一教學環節.下面節選了幾個學生的反饋.

生甲：從“最速降線”對于圖像的性質描繪，到“獵人打猴”學會作動態圖，到了解歐拉法理解“螞蟻追逐”問題，再到后來模擬科里奧利力和行星軌道問題……雖說在編程的過程中出現了很多問題……每次的編程都鍛煉了我們的思考能力.

生乙：在學習并且運用了Matlab后才領略到它讓數學物理問題的解決真的輕松了很多，比起其他編程語言，Matlab比較專注于數學計算這一塊，總之真的很便利.然后就是對物理素養的鍛煉，在處理問題中，通過自己運用物理知識來規定算法，可以加深對物理過程、物理公式，以及相應數學知識的理解和掌握，從理論知識跳躍到實際的運用.我覺得對我以后專業的學習也會有很大的幫助.

生丙：我們不斷地運用微積分的相關知識分析物體的運動，很大程度上加深了本組組員對微元法和歐拉法解運動學方程的認識、理解，而極坐標系的建立則簡化了我們需要處理的實際問題.所有的這些都加深了我們對物理實際問題的思考，為我們提供了解決問題的新思路.

教學實踐過程中也出現了一些問題，例如有的小組活動沒組織好，使得有些學生成了主力，其他學生成了輔助角色，以后的教學中將會在這方面加以注意，在開始形成規范的小組活動程序，引導良好的小組活動氛圍.希望我們的教學設計能對其他教師有借鑒意義.