均勻帶電平面折線在空間產生的電場及其可視化*

莫云飛

(長沙學院電子信息與電氣工程學院 湖南 長沙 410022)

周群益

(廣州理工學院通識教育學院 廣東 廣州 510540)

周麗麗

(贛南醫學院醫學信息工程學院 江西 贛州 341000)

侯兆陽

(長安大學理學院應用物理系 陜西 西安 710064)

1 引言

有論文利用直線電荷產生的電勢和電勢疊加原理推導出帶電三角形和四邊形在空間的電勢公式，利用電場與電勢的關系推導了電場的分布公式[1～6]．不過，這些公式都比較復雜，不便于計算．這些論文也沒有用圖形表示電勢和電場．

本文根據點電荷的電勢和電勢疊加原理推導了直線電荷在二維平面中產生的電勢的簡要公式，從而推導了直線電荷在三維空間中產生的電勢公式，又根據電勢疊加原理求帶電折線產生的電勢．利用電場與電勢之間的關系推導了電場強度的公式．將公式無量綱化，利用MATLAB計算了場強的分量，用等勢面和電場線直觀地反映了電場的分布規律．

2 均勻帶電線段的電勢

設平面折線有n條邊，其電荷線密度為λ(默認λ>0)，放置在xOy平面中．如圖1所示，在折線中取一條長為Li的邊，端點是Pi和Pi+1．在帶電線段上取一個線元，其電荷量dq=λdl，在場點P產生的電勢為

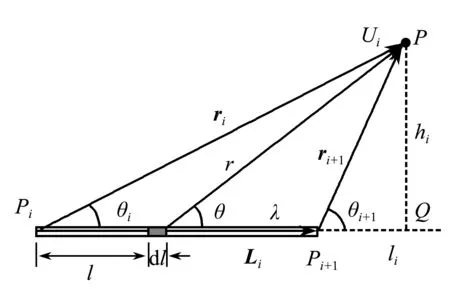
圖1 帶電線段產生的電勢

(1)

其中，k是靜電力常數．在直角三角形PPiQ中，hi和li是常數，hi=risinθi，li=ricosθi，由于

hi=rsinθl=li-rcosθ

(2)

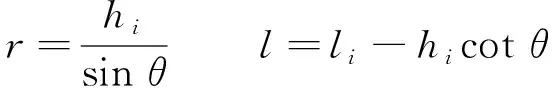
(3)

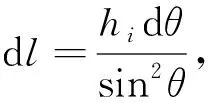
(4)

取無窮遠處為電勢零點，帶電線段在點P產生的電勢為

(5)

其中，θi和θi+1分別是點P與點Pi和Pi+1連線與橫軸之間的夾角．ri和ri+1分別是點P相對于端點Pi和Pi+1的徑矢，設連接Pi和Pi+1的矢量為Li，利用矢量點積的公式，兩個夾角分別為

(6)

3 帶電折線的電勢和場強

如圖2所示，在三維空間中，端點Pi和Pi+1的矢徑為

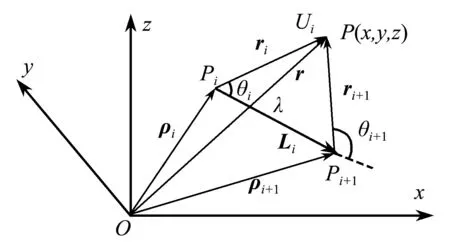
圖2 帶電線段在三維空間中的電勢

ρi=xii+yijρi+1=xi+1i+yi+1j

(7)

帶電的有向線段為

Li=ρi+1-ρi=(xi+1-xi)i+(yi+1-yi)j

(8)

長度為

(9)

點P(x,y,z)相對于端點Pi和Pi+1的矢徑分別為

(10)

其大小為

(11)

式(5)中的電勢Ui是空間坐標(x,y,z)的函數.帶電線段Li產生的場強為

(12)

(13)

式(12)有3個分量，每一個分量的公式都是比較復雜的．由于MATLAB的數值計算功能很強，不必將式(12)的右邊展開．

n條邊的帶電折線在三維空間中產生的總電勢為

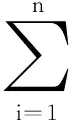
(14)

當U是常量時，式(14)就是等勢面方程．一般情況下，這是關于x，y和z的隱函數方程．

注意：n條邊的折線有n+1個端點，如果折線形成閉合多邊形，由于首尾相連，當i=n時，下標i+1就是1．

合場強為

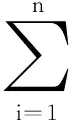
(15)

場強的3個分量決定了電場線，不過，電場線的方程很難求得．

4 公式無量綱化

電勢和場強公式是一種數學模型，根據模型設計程序，計算工作可用軟件MATLAB完成．不過，為了做純數值計算，需要將公式無量綱化．

取a為坐標單位，則場點P的無量綱坐標為

(16)

無量綱的線段矢量為

(17)

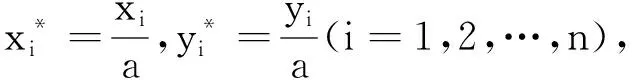
(18)

無量綱的矢徑大小分別為

(19)

取U0=kλ為電勢的單位，則線段產生的無量綱電勢為

(20)

無量綱的合電勢為

(21)

設

取E0為電場強度單位，則無量綱的電場強度為

(22)

(23)

將公式無量綱化即可設計MATLAB程序，做純數值計算并畫圖．

5 電場的可視化

利用MATLAB的計算功能和循環結構可以計算三維電勢，利用函數gradient可以計算電勢梯度即電場強度的3個分量，利用isosurface指令可以畫三維等勢面，利用流線指令streamline可以繪制三維電場線[7]．

(1)等腰折線的坐標為(a,0)，(0,a) 和(-a,0)，帶電折線的等勢面和電場線如圖3所示，等勢面本來是上下對稱的封閉曲面，這里只取下半部分；電勢從外到內依次是2U0，3U0，…，10U0，當電勢比較小時，等勢面分布在外面；隨著電勢的增加，等勢面向內移，前面的曲面向內彎曲；當電勢很高時，等勢面就包圍了帶電線段．電場線從帶電線段出發，垂直穿過等勢面，呈現排斥的形狀延伸到無窮遠處．在電荷附近，等勢面和電場線都比較密集，離電荷越遠，等勢面和電場線就越稀疏．等勢面和電場線是上下左右對稱的，這是因為兩段電荷左右對稱地分布在水平面上．

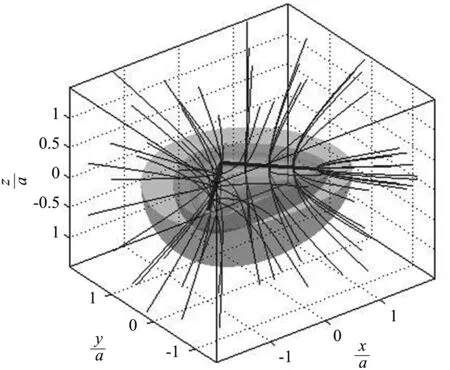
圖3 帶電等腰折線的三維等勢面和電場線

(2)如圖4所示，等腰三角形的坐標為 (a,0)，(0,a) 和(-a,0)，第3點與第1點封閉起來，電勢從外到內依次是3U0，4U0，…，10U0，當電勢比較低時，等勢面在外包圍整個三角形，如同層層相套的“碗”；當電勢比較高時，三角形的內部也出現等勢面；當電勢很高時，等勢面如筒狀包圍三角形．電場線從帶電三角形上發出，在中間出現排斥的形狀，延伸到無窮遠處．電場線垂直穿過等勢面，上下左右對稱分布．

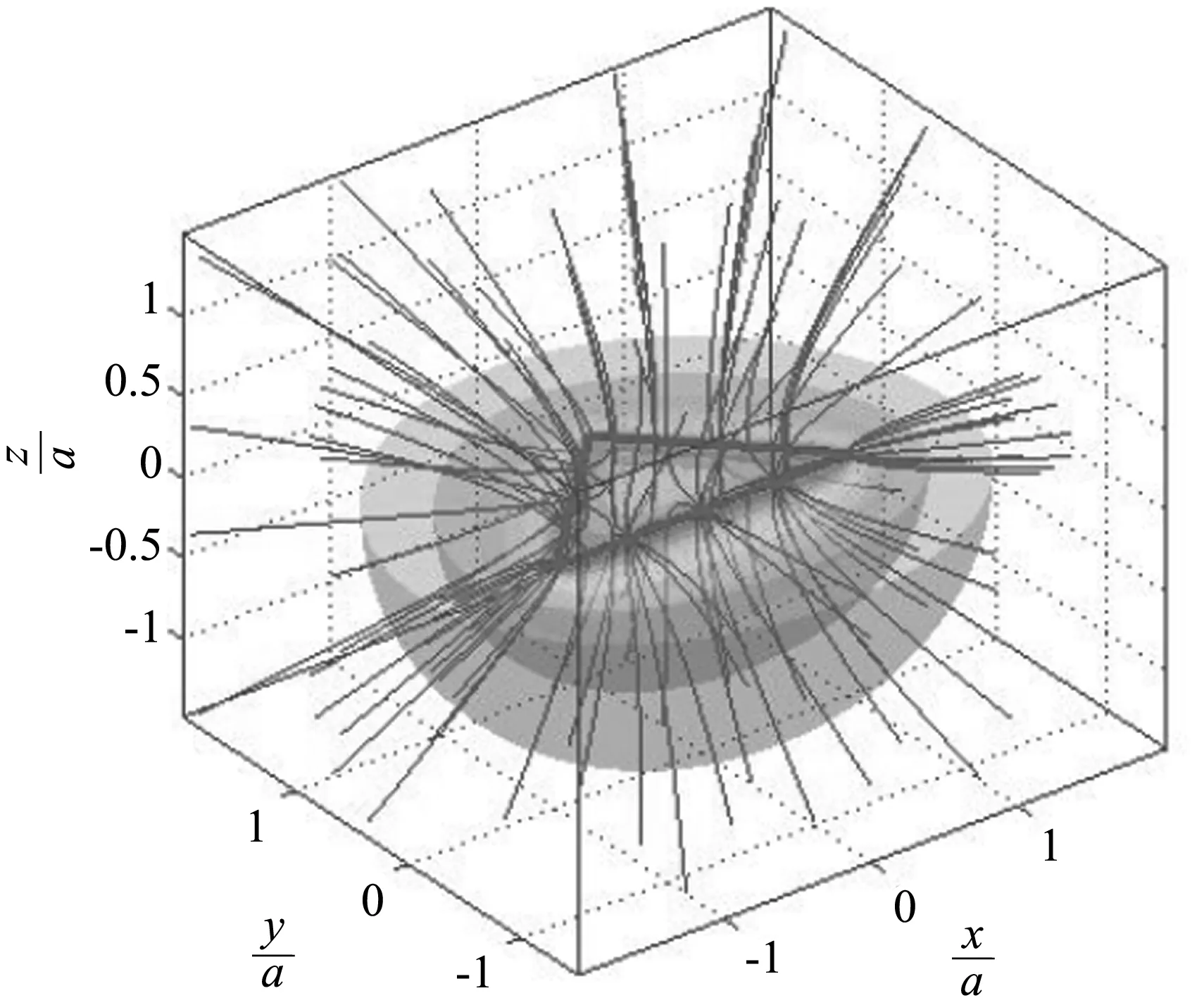
圖4 帶電等腰三角形的三維等勢面和電場線

(3)正四邊形的坐標為(a,a)，(-a,a)，(-a,-a)和(-a,a)，帶電正四邊的等勢面和電場線如圖5所示，等勢面接近于方形的“碗”， 從外到內的電勢依次是5U0，6U0，…，10U0；電場線上下，左右和前后都是對稱的．將坐標改為(a,b)，(-a,b)，(-a,-b)和(-a,b)，如果取b= 0.9a，則可形成帶電矩形的類似等勢面和電場線(圖略)．如果取b=1.2a，則等勢面和電場線也類似(圖略)．

圖5 帶電正四邊形的三維等勢面和電場線

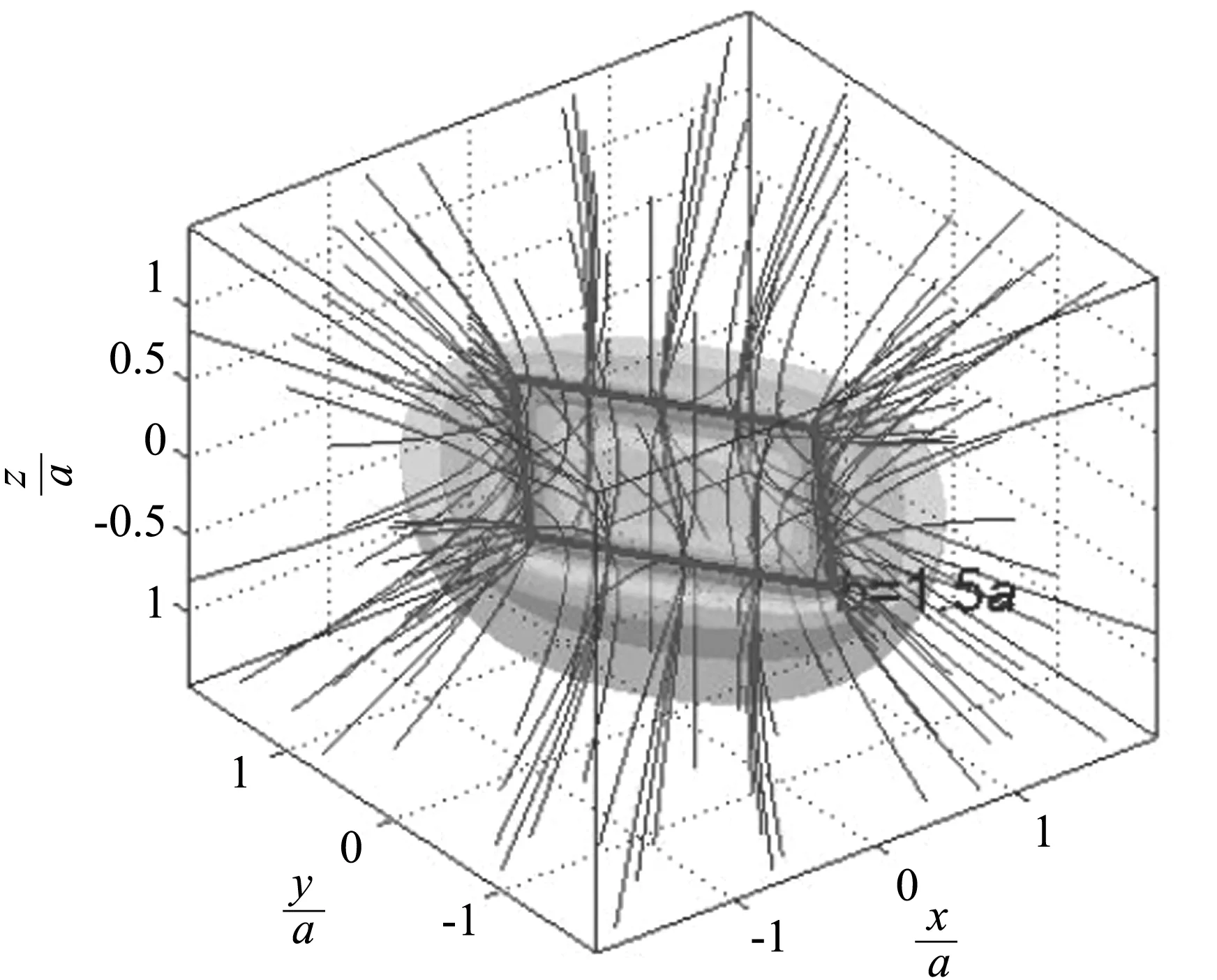
圖6 帶電棱形的三維等勢面和電場線

(5)帶電正6邊形的等勢面和電場線如圖7所示．用相同的方法也可以繪制其他正多邊形的等勢面和電場線(圖略)．

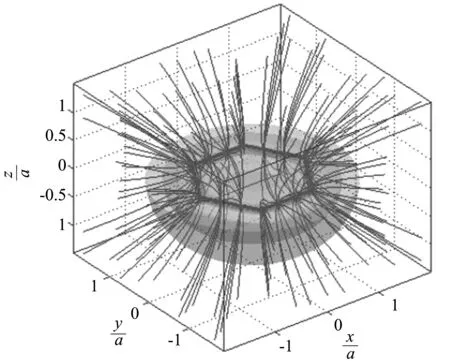
圖7 帶電正六邊形的三維等勢面和電場線

(6)帶電正24邊形的等勢面和電場線如圖8所示，等勢面接近于半球面．24邊形與圓比較接近，其等勢面和電場線接近于圓的等勢面和電場線．

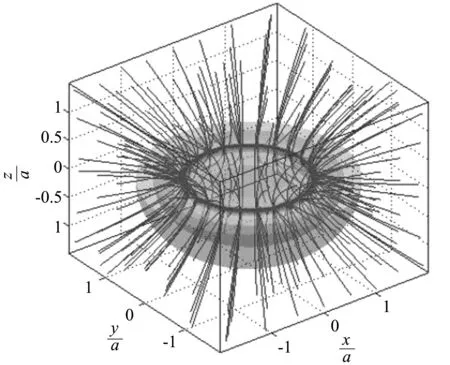
圖8 帶電正24邊形的三維等勢面和電場線

由此可見,利用MATLAB可以畫出帶電折線和任意多邊形的等勢面和電場線．

6 結束語

平面折線和多邊形只是坐標有所不同．在三維空間中，帶電線段電勢的公式比較簡單，電場強度的公式卻十分復雜，折線和多邊形的電場強度公式更加復雜．只要建立了數學模型，不論公式多么復雜，都能用MATLAB精確計算，還能繪制等勢面和電場線的圖形．由此可見,掌握了MATLAB的指令和程序設計方法，可以全面解決這類問題．這種方法還可以解決平面任意多邊形電流產生的磁場的計算和可視化問題．