磁約束問題中守恒量的討論

魯 斌 馮子江

(浙江省余姚中學(xué) 浙江 寧波 315400)

“磁約束”在高中物理中常有涉及.人教版物理選修3-5“核聚變”一節(jié)中提到：“帶電粒子運動時在均勻磁場中會由于洛倫茲力的作用而不飛散，因此有可能利用磁場來約束參加反應(yīng)的物質(zhì)，這就是磁約束.”并有“環(huán)流器” 的配圖(圖1).對于環(huán)流器的原理，我們往往從“磁鏡”的角度入手.本文提供兩個方案推導(dǎo)磁約束問題中的守恒量，并給出需要滿足的條件.

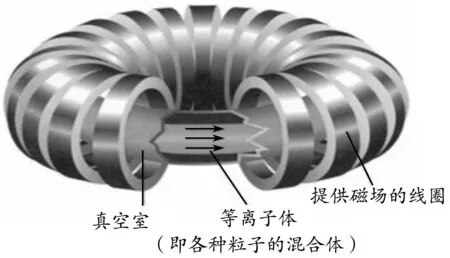
圖1 環(huán)流器(即tokamak )

1 從高斯定理到磁矩守恒

1.1 高斯定理

如圖2所示，空間中有“磁鏡”結(jié)構(gòu)的磁場分布，在任意位置取一高斯面S.

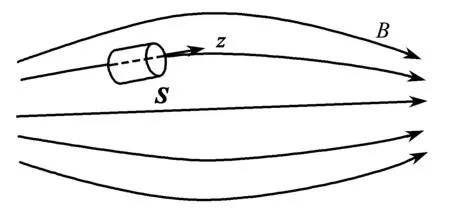
圖2 磁場分布

將圖2中的高斯面S放大如圖3所示，磁場沿z軸方向的分量為Bz，沿半徑方向的分量為Br，根據(jù)高斯定理

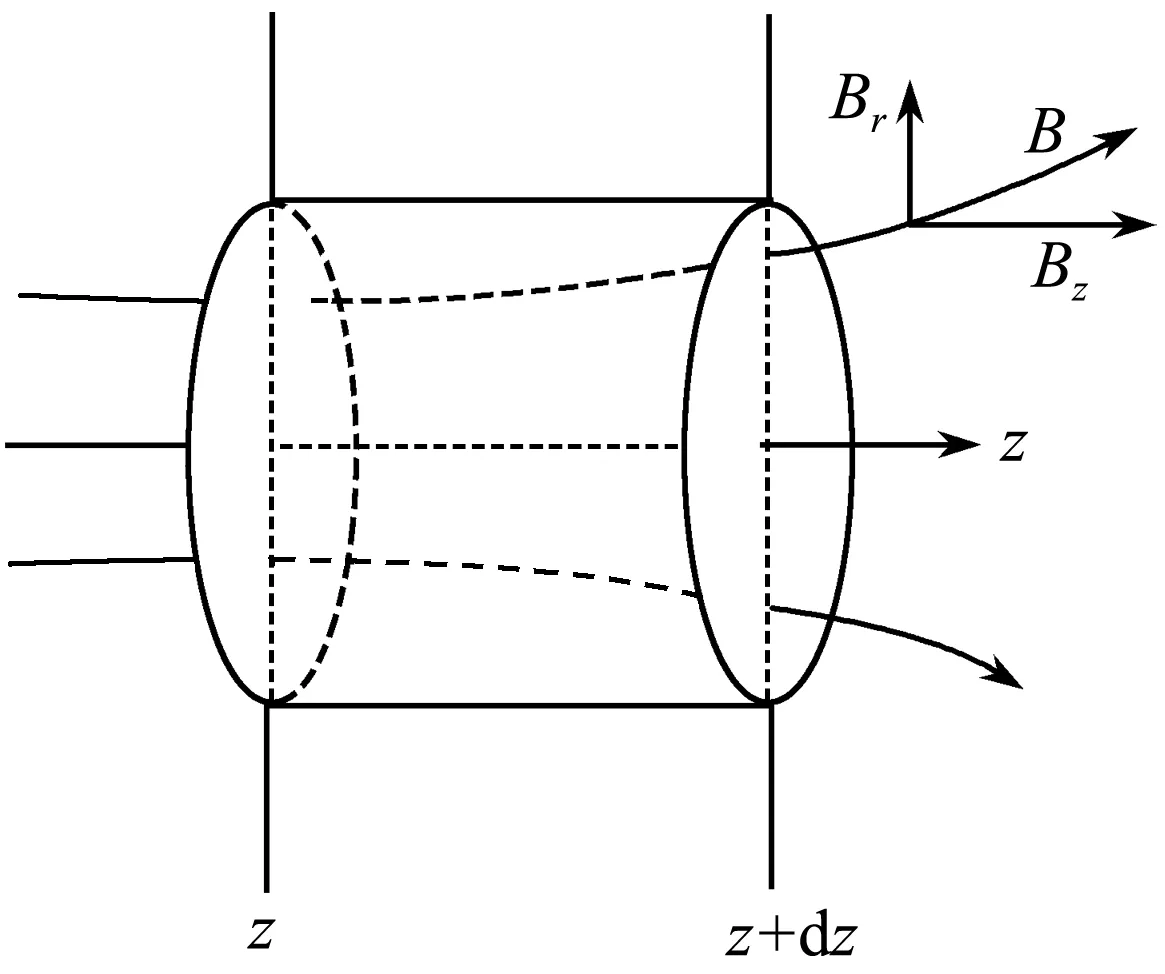
圖3 高斯面

Br2πrdz+Bz+dzπr2=Bzπr2

(1)

即有

得到

(2)

1.2 帶電粒子的運動

假設(shè)此時帶電粒子在磁場中運動的軌跡為虛線1(圖4).

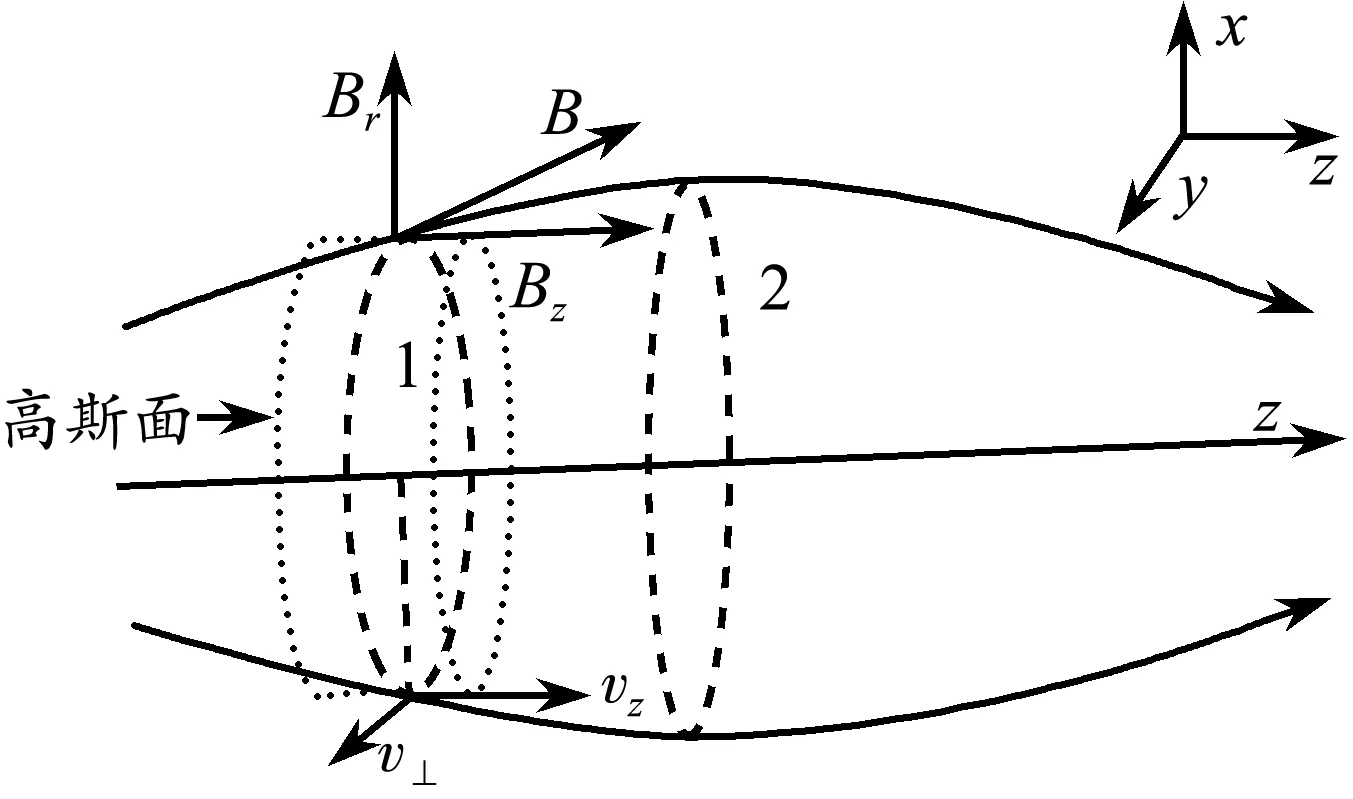
圖4 磁鏡

在半徑方向，有

得到

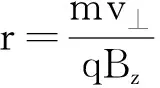
(3)

(4)

在z軸方向，有

(5)

將式(2)、(3)代入式(5)

(6)

又

(7)

式(7)代入式(6)后兩邊同乘以vz，有

(8)

根據(jù)能量守恒

(9)

將式(9)代入式(8)，有

(10)

1.3 磁矩

根據(jù)磁矩的定義

(11)

將式(3)、(4)代入式(11)，得到

(12)

1.4 磁矩守恒

將式(12)代入式(10)，有

(13)

則磁矩μ為常量.即在此過程中，磁矩為守恒量.即有

(14)

1.5 關(guān)于守恒量的討論

在上述推導(dǎo)中存在一定的近似.主要問題在于要保證帶電粒子繞磁場運動的曲率半徑r和高斯面的r保持一致.這樣才可將式(2)代入式(5)求解.實際上，由于磁場為非均勻場，導(dǎo)致帶電粒子的運動并非等距、等半徑的螺旋線，而是在高斯面附近的螺旋運動(圖5).

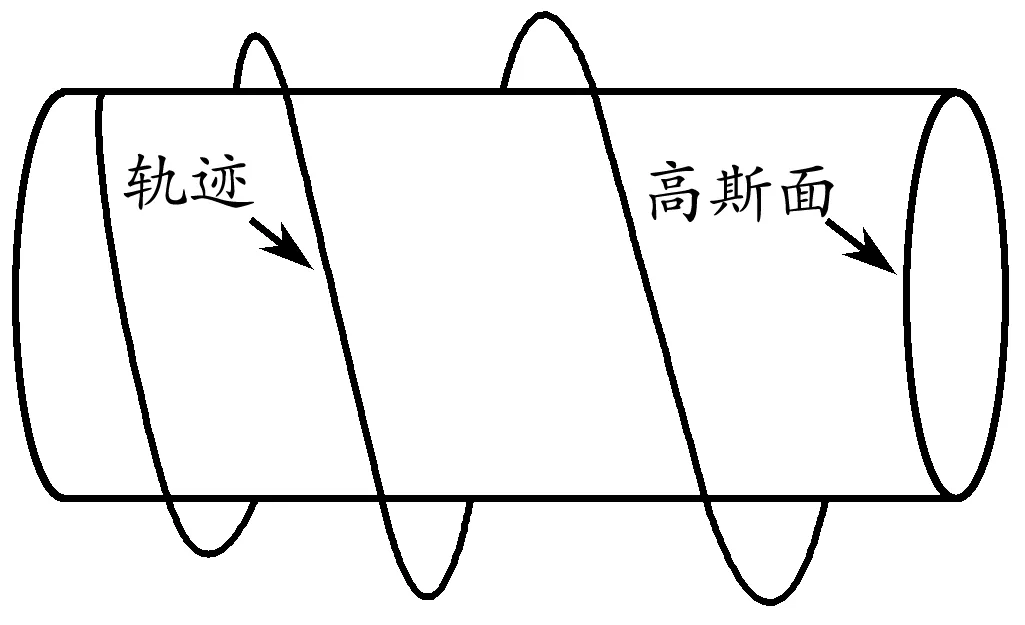
圖5 軌跡與高斯面

2 從渦旋電場到守恒量

2.1 渦旋電場做功

參照圖4，粒子在1位置運動時，從右往左觀察，粒子運動方向、磁感應(yīng)強(qiáng)度方向如圖6所示.

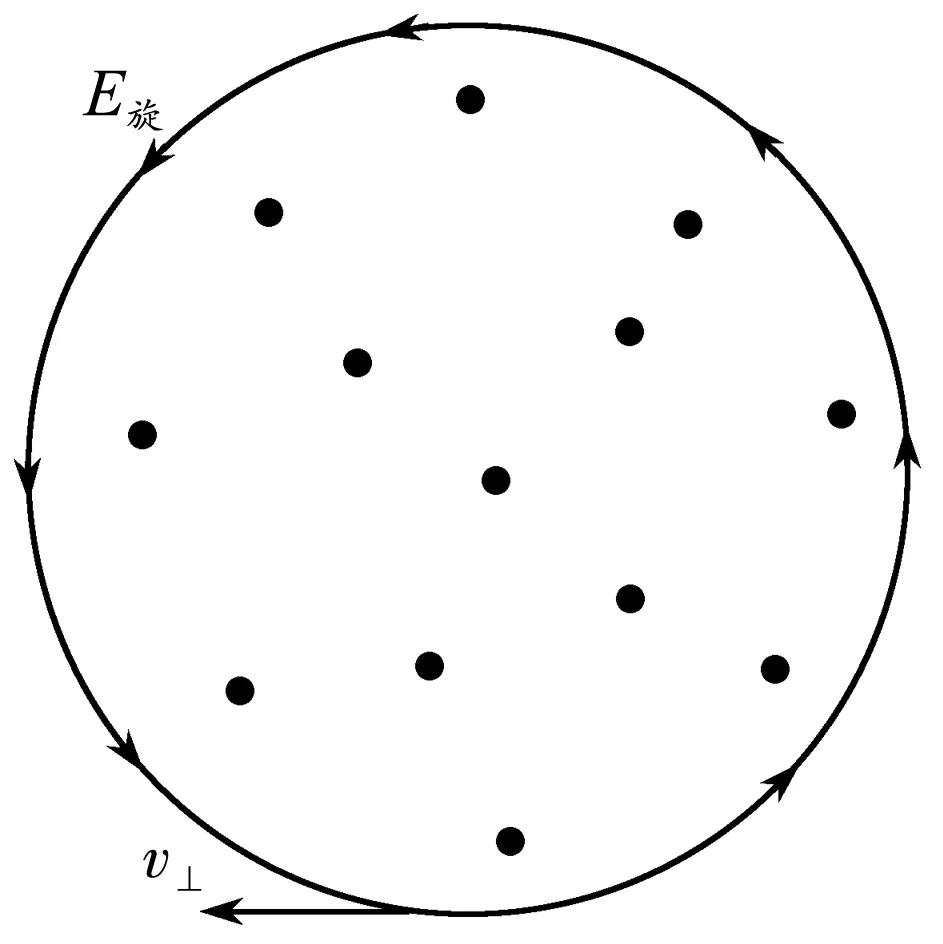
圖6 磁場方向與渦旋電場

可以將粒子從1位置運動到2位置的過程等效為粒子的運動平面不變，磁場逐漸減小的過程.由于磁通量的變化，在空間中產(chǎn)生渦旋電場，其方向如圖6中E旋所示.此時渦旋電場的方向與電子運動方向相反，繞行一圈的過程中，根據(jù)動能定理，有

(15)

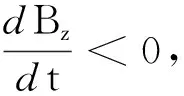
2.2 近似處理

(16)

繞行一周所需的時間T滿足式(4)，m的數(shù)量級為10-31，q的數(shù)量級為10-19,磁約束問題中，Bz一般也不會太小，故滿足

則有

dz=vzdt≈vzT

(17)

2.3 守恒量的推導(dǎo)

將式(4)、(16)、(17)代入式(15)，得到

(18)

兩邊同時積分，有

(19)

則有

(20)

此式即為磁矩守恒.

2.4 關(guān)于守恒量的討論

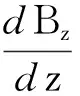
2.5 另一個方法

我們也可直接從動量定理進(jìn)行考查

則

(21)

此時從渦旋電場的方向與電子運動方向相反，有

-Eqdt=mdv⊥

(22)

將式(3)、(21)代入式(22)，得到

兩式同時積分，有

(23)

式(23)與磁矩守恒等價.此方法要求渦旋電場線和運動軌跡嚴(yán)格重合.實際上，由于磁場的非均勻性，這兩者存在微小偏差.

3 關(guān)于角動量守恒的條件

許多文獻(xiàn)利用角動量守恒來導(dǎo)出守恒量.如圖7所示，洛倫茲力的方向指向軸線，則在z軸方向角動量守恒，有

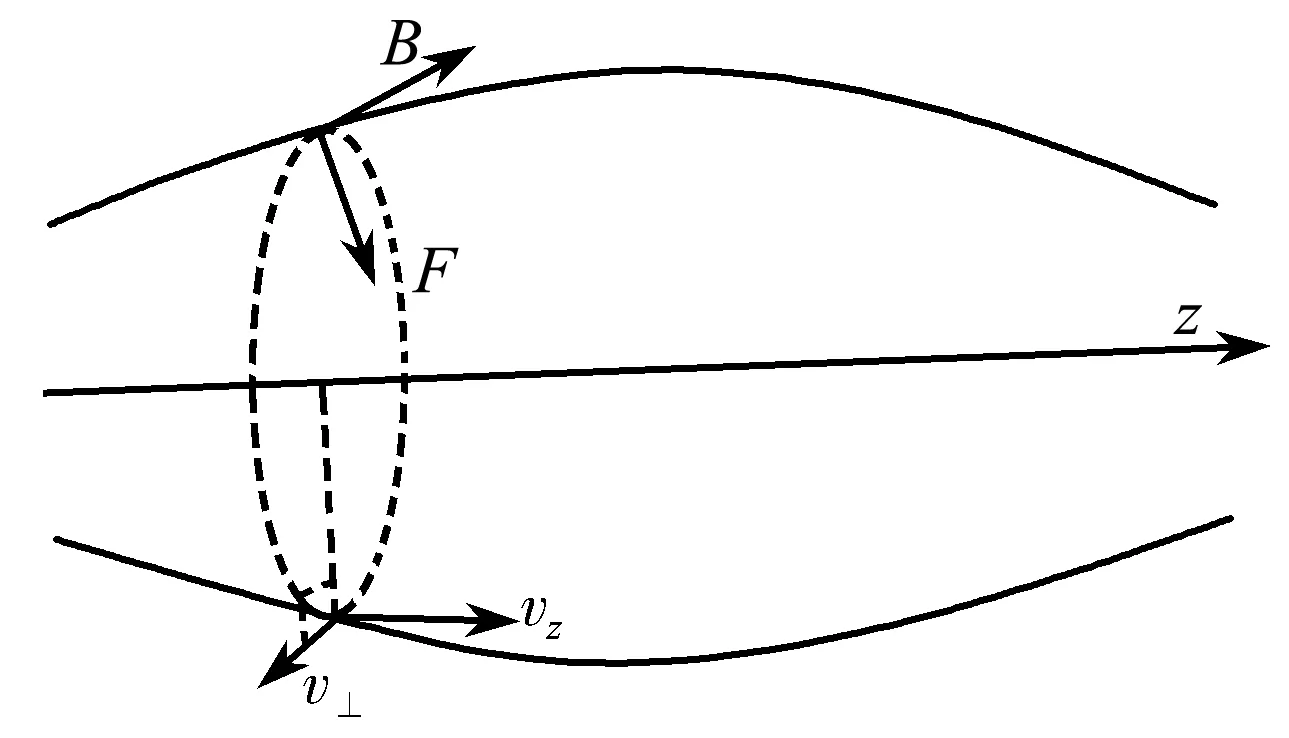
圖7 角動量

L=mv⊥r=C

(24)

將式(3)代入式(24)，有

(25)

對于確定的粒子，m和q都是常數(shù)，則角動量守恒與磁矩守恒是等價的.此推導(dǎo)的前提是洛倫茲力始終指向軸線，圓心總落在軸上.

如圖8所示，由于粒子所做的是螺旋運動，其受力不總是指向軸線，其圓心也不總是落在軸線.但如果磁場隨空間變化緩慢，則螺旋線與圓周的偏差不大，可保證受力與軸線偏差不大，從而保證角動量近似守恒.

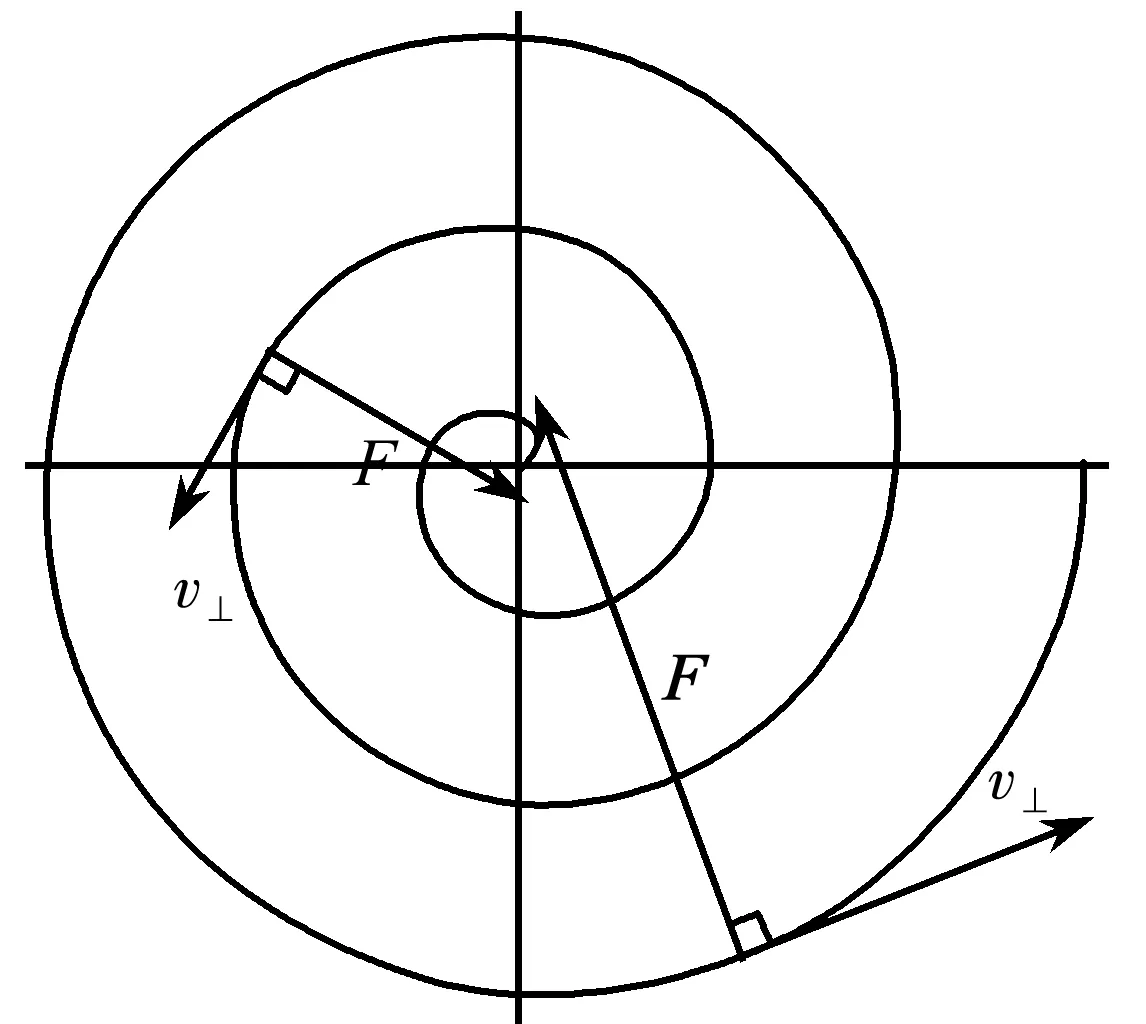
圖8 螺旋線運動

4 結(jié)束語

磁約束問題還有著廣泛的運用.如圖9所示，帶電粒子(如宇宙射線的帶電粒子)被地磁場捕獲，繞地磁感應(yīng)線做螺旋線運動，在近兩極處地磁場增強(qiáng)，做螺旋運動的粒子被折回，結(jié)果沿磁力線來回振蕩形成范阿侖輻射帶.

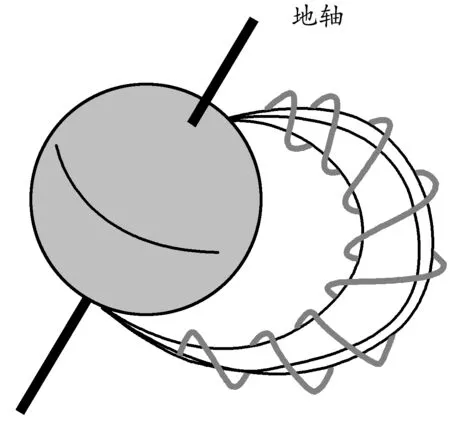
圖9 范阿侖輻射帶

由于地球體積很大，地磁場隨空間的變化非常緩慢，宇宙粒子在運動過程中近似滿足“磁矩守恒”或者“角動量”守恒.

若帶電粒子無法滿足折返條件，粒子在兩極處的磁力線引導(dǎo)下，在兩極附近進(jìn)入大氣層，與大氣中的原子和分子碰撞并激發(fā)，產(chǎn)生光芒，形成極光.