麥克納姆輪移動底盤的自適應滑模控制器設計

江夢林，趙德權，孫永福，王玉超

（四川農業大學 機電學院，雅安 625014）

0 引言

相對于傳統的移動機器人，全方位移動機器人因為具有良好的機動性能，能夠實現全向移動并且轉彎半徑為零，因而被廣泛的應用到各個場合下，比如家庭服務、倉庫以及醫療等行業[1～3]。而基于麥克納姆輪的移動機器人因其承載能力強運動連續的特點，使其在工業和學術領域得到了越來越多的關注。麥克納姆輪是由主動輪和一系列的從動輪組成，從動輪通常和主動輪的輪輻存在45°的夾角[4,5]。通過四個麥克納姆輪的協同作用就可以實現全方位移動。

隨著制造業的迅速發展，移動機械臂得到了越來越多的應用，為了提高移動機械臂的移動能力和靈活性，許多學者嘗試將麥克納姆輪移動機器人作為移動機械臂的底盤[6]。值得一說的是，移動底盤軌跡跟蹤的精度是保證移動作業質量的關鍵。因此，設計一個高精度的軌跡跟蹤控制器來保證跟蹤精度是很有必要的。然而，在實際環境中，外部的擾動和模型的不確定性是真實存在的，這將會導致系統不穩定。因此，對于麥克納姆輪移動機器人的軌跡跟蹤控制依然是一個挑戰。

為了克服上述的問題，諸多的學者完成了對麥克納姆輪移動機器人的運動學和動力學建模[7～9]。在其運動學和動力學模型的基礎上，學者們提出了許多的控制策略。主要的方法包括自適應控制[10～11]，反演算法[12～14]以及神經網絡等[15～17]。文獻[10]針對輪式移動機器人設計了一種自適應軌跡跟蹤控制器，該控制方法可以減小模型中未知參數和不確定性的影響。文獻[11]針對非完整輪式機器人提出了一個非線性自適應控制器，通過輸入輸出反饋線性化技術獲得了給定系統不確定參數的估計值。自適應控制依賴于系統的精確模型，但是精確的系統模型通常是難以建立的。反演算法主要應用于一系列滿足嚴格反饋的系統。反演控制通常和其他的控制方法結合起來使用。文獻[12]中對于一類含有不確定性的非線性動力系統設計了一種改進的反演控制器。文獻[13]將反演控制和自適應控制結合起來，在考慮外加擾動以及不確定性的情況下，對麥克納姆輪全向機器人設計了一個非線性自適應控制器。文獻[14]將該方法和小波神經網絡相結合設計了一個控制器來實現軌跡跟蹤，小波神經網絡被用來逼近系統中的不確定項。神經網絡技術因為其強大的學習能力，適合用來控制復雜的動力系統。在文獻[15]和文獻[16]中，徑向基神經網絡被成功的用來逼近系統中的未建模不確定性。文獻[17]基于滑模控制提出了一種自適應神經網絡的控制方法，通過神經網絡來逼近模型的不確定性和外部干擾。

作為另外一種重要的控制方法，滑模控制因其抗干擾能力強而得到廣泛的應用。文獻[5]和文獻[18]針對麥克納姆輪全向移動機器人分別提出了基于擴展狀態觀測器的滑模控制策略和非奇異終端滑模控制器。滑模控制的主要缺點就是由于控制器的不連續會導致抖震現象。為了抑制這種現象，文獻[19]提出了高階滑模控制策略。文獻[20]設計了一種自適應滑模控制器。

本文針對麥克納姆輪全向移動機器人系統設計一個軌跡跟蹤控制器。首先，使用徑向基神經網絡來逼近系統中的不確定項以及外部擾動。和文獻[17]不同的是，徑向基神經網絡的權值的范數和估計誤差的范數通過具有σ修正的自適應學習法則來估計[21～22]。其次，通過自適應學習法則得到的未知參數估計值進而設計了一個自適應滑模控制器。再者，通過Lyapunov理論分析了該控制方法的穩定性和魯棒性。最后通過仿真驗證了所提出方法的有效性。

1 數學模型的建立

1.1 麥克納姆輪移動機器人的運動學模型

麥克納姆移動機器人的坐標系如圖1所示，其中X-O-Y，Xb-Ob-Yb，Xwi-Owi-Ywi(i=1,2,3,4)分別為世界坐標系、連體坐標系和輪系坐標系。Ob和移動機器人的幾何中心重合。(x,y,φ)為移動機器人在世界坐標系下的位姿。(xi,yi,βi)為第i個輪子在連體坐標系下的位姿。γi為第i輪子的從動輪和主動輪輪輻之間的夾角。

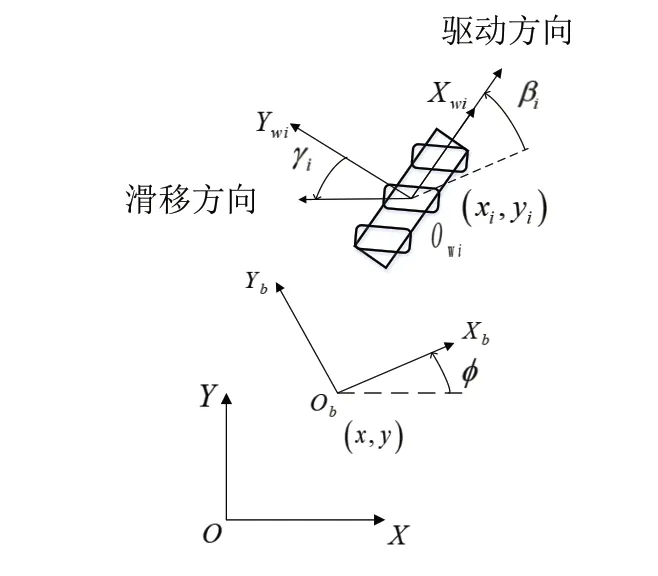
圖1 麥克納姆輪移動機器人的坐標系轉換

令q=[x y φ]，通過坐標系的轉換可以的到第i個輪子的轉速和之間的關系為[23]：

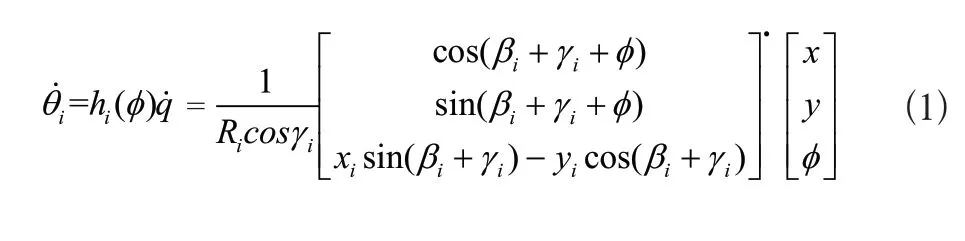
其中，Ri為第i個輪子的半徑。麥克納姆輪移動機器人的結構示意圖如圖2所示。其中，W和L分別為移動機器人長度和寬度的一半。由圖2可知，β1β2β3β4=0，｜xi｜=W,｜yi｜=L,γ1=γ4=-45°,γ1=γ4=45°。此外令R1=R2=R3=R4=R，定義移動機器人輪子的轉動角θ=[θ1θ2θ3θ4]·，移動機器人在連體坐標系下的速度Vb=[vxvyωz]，Vb與姿態角無關即φ=0，根據式(1)可以的到移動機器人在連體坐標系下的逆運動學方程為：

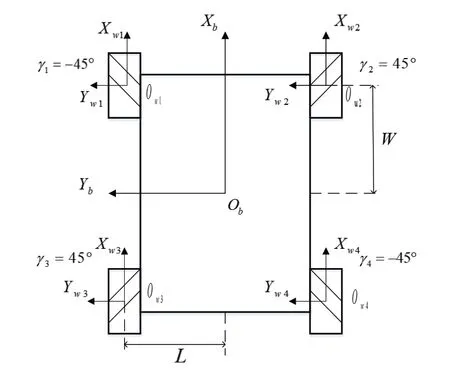
圖2 麥克納姆輪全向移動機器人的結構示意圖

轉換矩陣H(0)存在偽逆矩陣：

則移動機器人的正運動學公式可以描述如下：

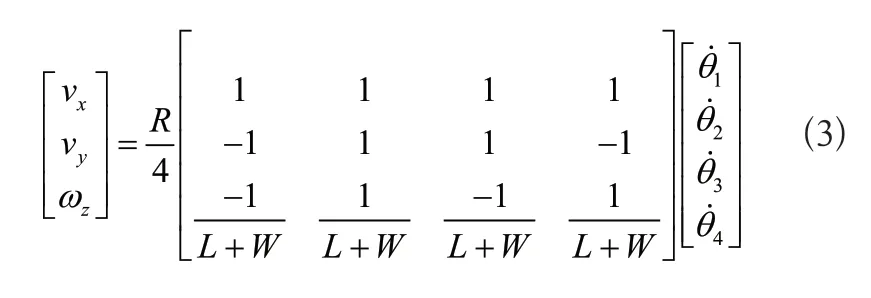
進一步展開為如下形式：

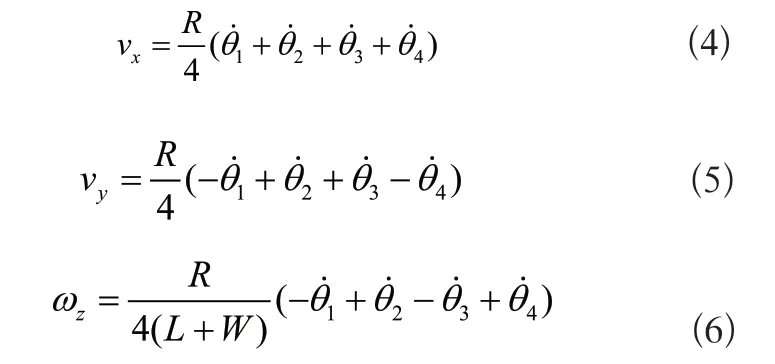
同理，根據式(1)移動機器人在世界坐標系下的逆運動學方程為：

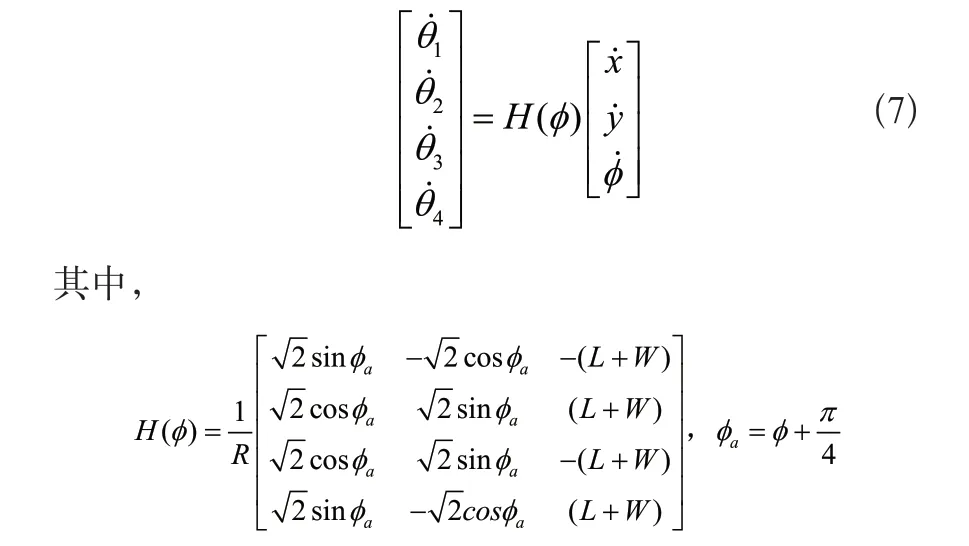
同理H(φ)也存在偽逆矩陣，那么移動機器人在世界坐標系下的正運動學方程為：

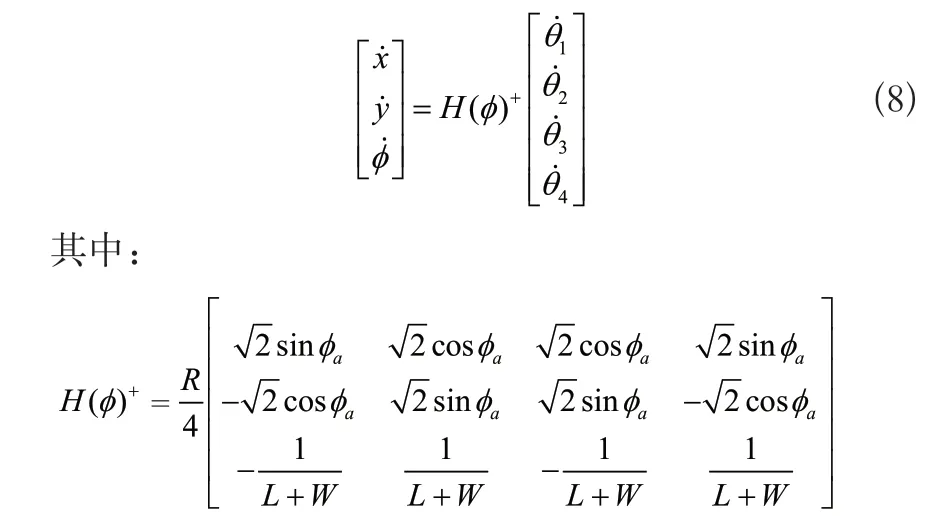
1.2 麥克納姆輪移動機器人的動力學建模

本文使用拉格朗日法來建立移動機器人的動力學模型[7]，拉格朗日算子的表達式為：

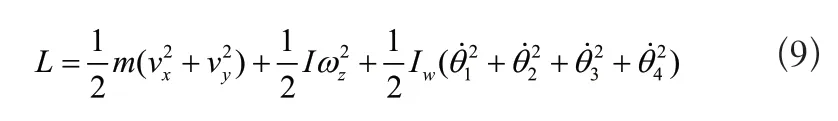
其中m是總的質量，I和Iw分別是移動機器人繞其幾何中心的轉動慣量和輪子繞其轉軸的轉動慣量。vx，vy，ωz如式(4)～式(6)所示。

拉格朗日方程表述如下：

其中，

τ=[τ1τ2τ3τ4],τd=[τd1τd2τd3τd4]分別為輸入轉矩向量和外部擾動向量且τd是連續有界的，滿足‖τd‖≤d*＜∞，d*是未知的正數。D為粘滯摩擦力：

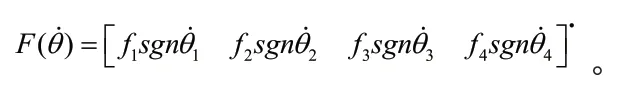
通過計算拉格朗日方程，移動機器人的動力學模型的表述如下：

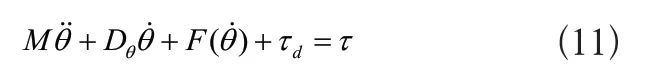
考慮系統的不確定性，可以得到一個新的動力學模型如下：

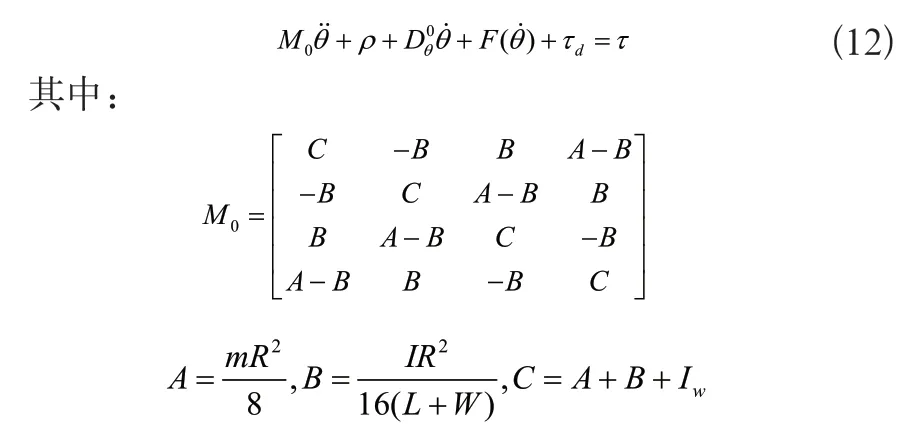
不確定項ρ=ΔMθ+ΔDθθ，ρ是有界的且滿足是一個未知的常數。

結合式(7)～式(12)，動力學模型變成如下形式：

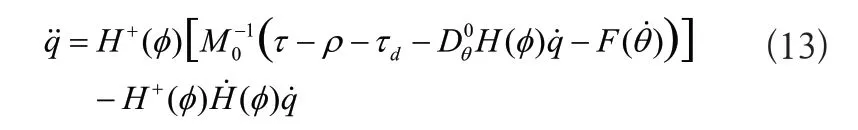
式(13)可以進一步改寫成：

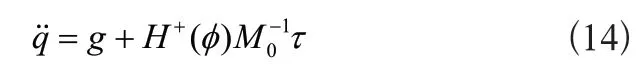
其中不確定項：

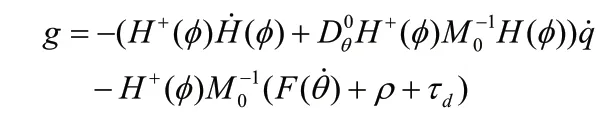
2 自適應滑模控制器設計

本節旨在針對麥克納姆輪移動機器人，在考慮外部擾動、模型不確定性的條件下，基于移動機器人的動力系模型設計一個自適應滑模控制器，使移動機器人能夠精確地跟蹤參考軌跡qd，引入徑向基神經網絡來逼近不確定項，令理想軌跡qd=[xdydφd]是二階可導的。控制目標是設計一個輸入轉矩τ使得q→qd。

首先定義位姿誤差e=q-qd，則，將滑模面定義為如下形式：

對式(15)求導：

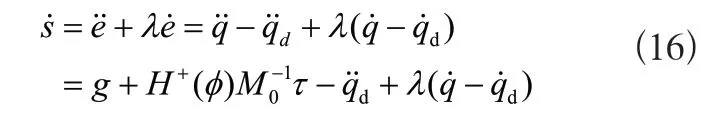
本文引入徑向基神經網絡來逼近不確定項g，其結構簡圖如圖3所示。

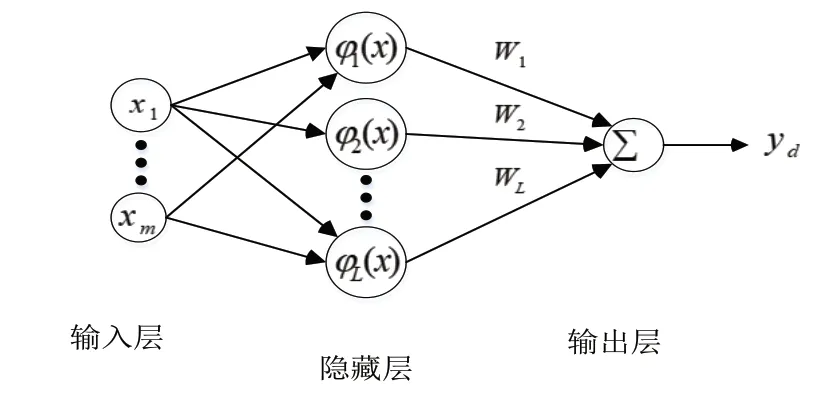
圖3 徑向基神經網絡的結構見圖

如文獻[2 2]所述，對于一個連續光滑的函數h(xin)∶Rm→Rn，存在一個徑向基神經網絡使得：

其中xin∈Rm是輸入向量，φh(.)∈RL是基函數，L代表神經元的個數，wh∈RL×n是輸出層的權值矩陣，εxm∈Rn是逼近誤差且滿足‖εxin‖≤是一個未知的常數。通過引入上述神經網絡，式(16)變成如下形式：

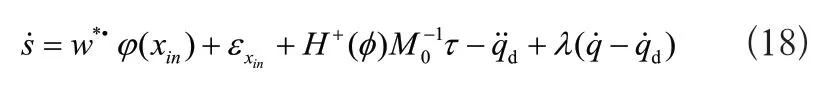
將滑模趨近律設計為如下形式[16]：

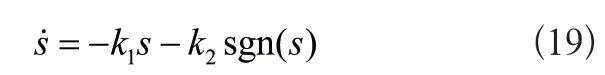
式中k1，k2是常數矩陣，sgn(s)是符號函數，滿足:

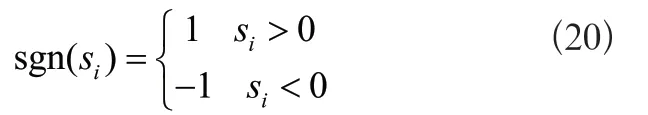
選取Lyapunov函數為:

3 仿真實驗與分析

本節將通過兩組仿真實驗來驗證本文所提出的控制器的有效性，為了驗證控制器的魯棒性，本文將質量設計為時變的，同時在系統中加入了余弦形式的擾動。一組仿真實驗的參考軌跡是一個圓形，另一組仿真實驗的參考軌跡是紐帶形。移動機器人的參數如表1所示。

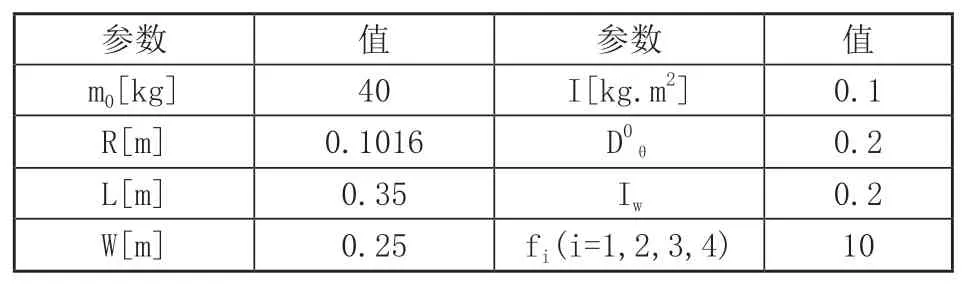
表1 麥克納姆輪移動機器人的結構參數

此外，為了逼近不確定項g，本文將使用高斯函數作為徑向基神經網絡的基函數，形式如下：

2）仿真實驗2：紐帶形參考軌跡

紐帶形參考軌跡的表達式如下：

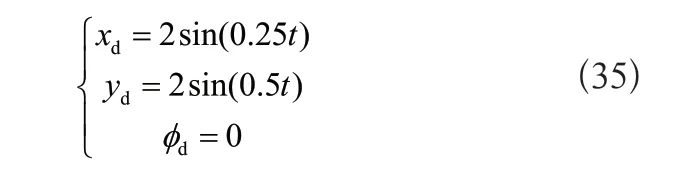
和仿真實驗1相同，將總的質量設計為時變的，同時加入余弦形式的擾動。移動機器人的初始位置[x0y0φ0]·=[0.2 0.2 0.2]·控制參數選擇如下：

移動機器人軌跡跟蹤的結果如圖4和圖8所示，可以知道移動機器人在存在擾動且質量為時變情況下依然能夠很好的跟蹤上參考軌跡，具有較強的魯棒性。圖5和圖9是軌跡跟蹤的誤差，可以看到移動機器人的跟蹤誤差分別小于0.1m和0.05m且跟蹤誤差是一致最終有界的。自適應學習法則的估計結果如圖6和圖10所示，圖7和圖11是輸入轉矩，因為移動機器人的初始位置和參考軌跡具有一定的差距，所以在開始時需要的轉矩較大，跟蹤上參考軌跡后輸入轉矩減小，同時輸入也是一致最終有界的。通過上述的仿真結果，驗證了本文所設計的控制器具有良好的魯棒性能且跟蹤精度高的優點。

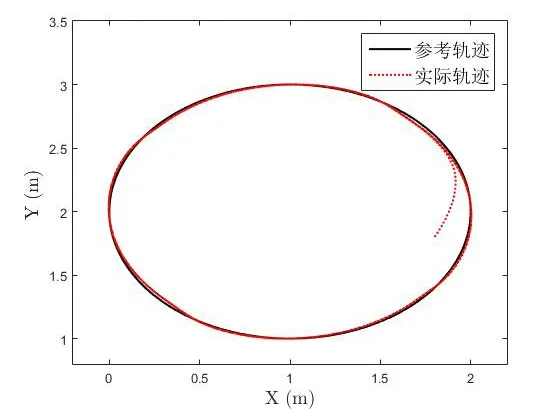
圖4 圓形參考軌跡的跟蹤結果

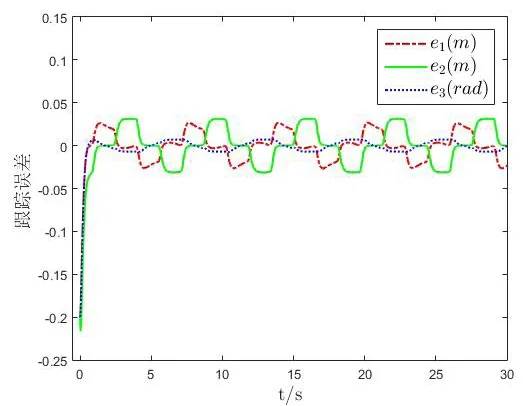
圖5 圓形參考軌跡的跟蹤誤差

圖6 圓形參考軌跡的自適應學習法則

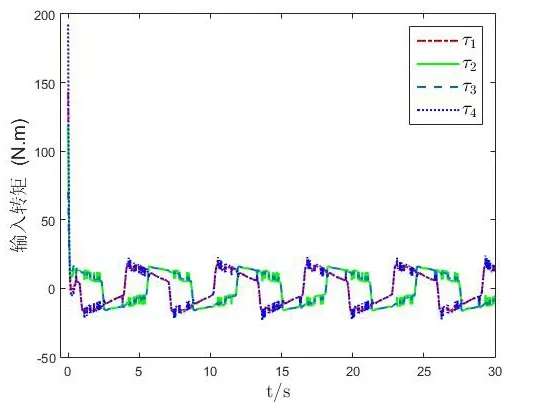
圖7 圓形參考軌跡的輸入轉矩

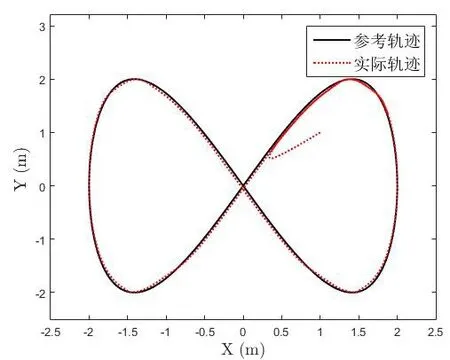
圖8 紐帶形參考軌跡的跟蹤結果

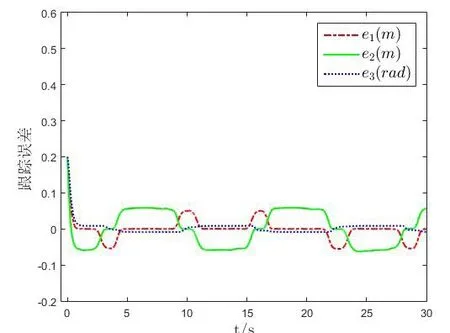
圖9 紐帶形參考軌跡的跟蹤誤差

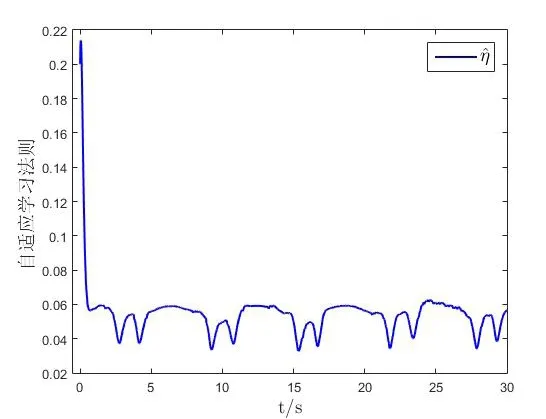
圖10 紐帶形參考軌跡的自適應學習法則

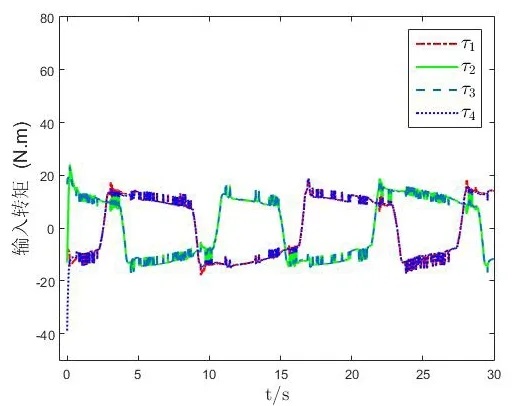
圖11 紐帶形參考軌跡的輸入轉矩

4 結語

本文針對麥克納姆輪全向移動機器人的軌跡跟蹤問題，在其動力學模型的基礎上設計了一個自適應滑模控制器。同時還考慮了參數變化和外部干擾，首先，本文引入徑向基神經網絡來逼近系統中的不確定項，徑向基神經網絡的權值的范數和逼近誤差的范數的估計值通過σ修正的自適應學習法則來獲得。其次，通過Lyapunov穩定性分析論證了本文提出的控制器能夠保證系統的一致最終有界。最后兩組仿真實驗驗證了控制器的有效。