某金礦礦巖尺寸效應性質試驗研究及應用

孫國文 王 剛 蔡 泳 鄭 杰 成 墻 梁秦銘 晏 偉 黃金涌

(1.重慶工程職業技術學院科技處,重慶 400000;2.紫金礦業集團股份有限公司,廈門 361000;3.煤礦災害動力學與控制國家重點實驗室,重慶 400000;4.重慶大學資源與安全學院,重慶 400000)

在礦山開采設計中,礦柱尺寸關系到采場結構穩定性和回采率。因此,根據礦山實際確定好合理礦柱尺寸是礦山生產經營活動的重要環節。根據我國應急管理部所公布的數據,2013—2017 年我國非煤礦山由于采空區失穩導致的死亡人數和事故數分別占非煤礦山事故中首位[1]。所以合理確定好礦柱留設尺寸也是礦山安全生產的重要保證之一。由于巖石(巖體)是一個非均質材料,具有明顯的尺寸效應,其強度與幾何之間又并非呈簡單幾何相似規律。所以礦柱留設尺寸問題歸根結底是巖石(巖體)尺寸效應問題。

目前國內外關于巖石尺寸效應已有不少研究成果,主要集中于巖石形狀效應(不同高徑比試件)和巖石體積效應(高徑比一定,不同體積試件)兩大方面。王兆遠等[2]研究了不同尺寸下紅砂巖點荷載與單軸壓縮強度之間關系,研究發現紅砂巖點荷載強度具有明顯的尺寸效應;作者分析了形狀系數與點荷載之間關系,獲得點荷載預測單軸抗壓強度的經驗公式。伍法權等[3]研究了小尺寸下青砂巖和玄武巖尺寸效應規律,研究結果表明,小尺寸青砂巖與玄武巖并不遵循常規的尺寸效應規律,其強度隨尺寸的增大而增加;結合CT 掃描分析,作者指出巖石內部均勻分布的空隙影響著巖石尺寸效應規律。胡龍生[4]對不同高徑比煤巖巖樣進行了試驗,結果表明,煤巖強度隨高徑比增加而減小呈指數函數下降的趨勢,應用RFPA 數值模擬軟件得到相類似結果。郭國瀟等[5]研究了不同尺寸下花崗巖單軸抗壓強度,應用數字圖像處理技術建立起顆粒流計算模型,模擬結果表明,花崗巖強度隨尺寸增加而減少,花崗巖強度與其內部云母含量明顯相關,云母含量越多,力學性質越差。傅偉斌[6]研究了不同高徑比下花崗巖與灰巖尺寸效應,研究發現,花崗巖與灰巖單軸抗壓強度隨高徑比增大而減小,破裂形式也由復雜劈裂破壞轉為剪切破壞。

綜合各學者的研究成果可知,各種巖石尺寸效應規律不一致,一種類型巖石尺寸效應規律不能應用到另一種巖石工程背景中。鑒于此,本研究以某金礦礦巖為對象,通過室內力學試驗揭示了其尺寸效應規律,并分析了巖樣壓縮過程中聲發射信號和分形維數隨尺寸變化規律。最后基于研究結論,對某金礦試驗采場礦柱可回收性做出評估。

1 巖石尺寸效應理論模型分析

礦物通過結晶或膠結的方式形成巖石,所以巖石力學性質與礦物成分和結晶(膠結)形式緊密相關。在結晶(膠結)不良的地方會形成強度較低的“弱點”造成巖石的非均質性。如何定量定性地描述巖石中“弱點”對其力學性質影響是尺寸效應理論模型中要解決的關鍵點。常用描述巖石非均質性的分布函數主要有Weibull 分布函數和對數正態分布函數。

1.1 Weibull 強度尺寸效應理論模型

首先對巖石微元力學性質做出假設:① 認為巖石微元力學性質服從最弱鏈模型,鏈與鏈之間力學性質差異反映出巖石非均質性質;② 忽略加載過程中微裂紋相互搭接貫通所形成局部應力場。

則dσ應力區間內,單位體積巖石內所新形成微裂紋數量為

式中,n(σ)為濃度函數;σ為應力,MPa;N0為微裂紋條數。

在單軸試驗加載過程中,單位體積巖石微裂紋與應力關系如圖1所示。則巖石總體積內微裂紋數量為

圖1 微裂紋與應力關系Fig.1 The relationship between microcracks and stress

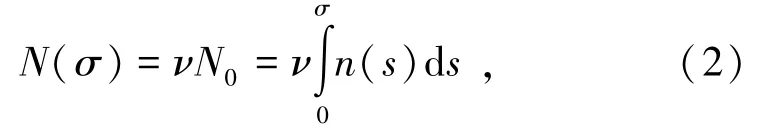
式中,ν為巖石體積,m3;N為巖石在加載過程中所形成微裂紋總量。

值得注意的是,N(σ)為加載過程中微裂紋的期望值,是統計平均值概念。對于單一樣本來說,巖石加載過程中微裂紋出現的數量可能各種各樣。按照數理統計理論,出現K個微裂紋的概率為

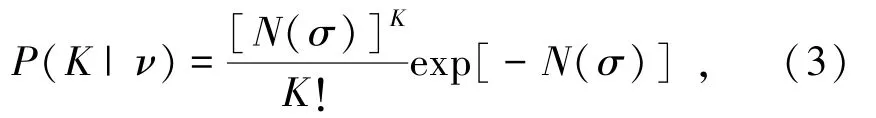
式中,P為概率;K為微裂紋數量,條。

基于最弱鏈模型只要一個缺陷就可能引發巖石失穩破壞,則有:

式中,Pf為巖石破壞概率。由數理統計知識可知,巖石破壞時平均應力為

式中,為巖石破壞時平均應力,MPa。

從式(4)可知,當σ為0 時,巖石破壞概率為0;當σ為正無窮大時,巖石破壞概率為1。符合直觀規律。

基于Weibull 分布,對濃度函數n(s),存在關系:

式中,ν0為參考體積,m3;σu為應力閾值,對于準脆性材料,σu= 0;m為巖石材料均質度,反映巖石內部均質程度;σ0為尺度參數,MPa。

聯立式(5)和式(6)可得:

式中,Γ為伽馬函數。

1.2 對數正態分布強度尺寸理論模型

按照上節分析方式,將Weibull 分布函數替換成對數正態分布函數,則可得出對數正態分布下巖石尺寸效應理論模型。

式中,σ0為尺度參數,可通過基準試件強度離散性系數得出,MPa;s為積分參量,無實際物理含義;Φ為標準正態分布函數;ξ為巖石非均質度,與參數m物理意義相反,其值越小說明巖石內部更均質。

2 巖石尺寸效應實驗方案及測試

2.1 實驗材料及方案

實驗材料取自某金礦礦巖,選取表面無明顯節理裂隙巖石托運至試件加工室。按照實驗方案鉆取出需求的尺寸如圖2所示。為探究巖石尺寸對其力學性質的影響設置了2 種試驗方案,形狀效應與體積效應試驗方案如表1。

圖2 巖石試件Fig.2 Rock specimen

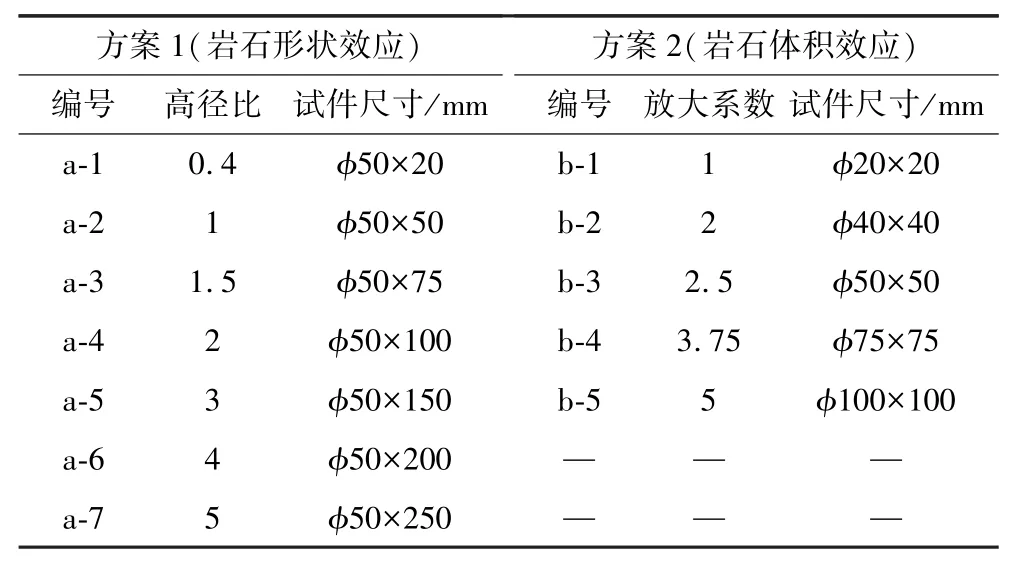
表1 實驗方案Table 1 Experimental scheme

2.2 實驗設備選擇

實驗測試系統如圖3所示。

圖3 試件測試示意Fig.3 Schematic of test specimen

(1)壓力機。選用島津公司生產AG-250kNIS 型號壓力機,其最大荷載為250 kN。可實現位移和荷載等多種加載方式控制。

(2)聲發射信號監測系統。選用美國PAC 公司生產PCI-2 型號聲發射儀,該聲發射儀具有12 通道可供聲信號采集,內置40 MHz,18 位A/D 轉化器可對聲發射信號實時進行高精度分析。

(3)應變監測系統。選用濟南西格馬公司生產ASMB2D-32 型應變儀對巖石表面形變進行測量。

2.3 實驗結果分析

2.3.1 應力應變分析

體積效應與形狀效應中單軸壓縮應力應變曲線如圖4所示。

圖4 單軸實驗應力應變曲線Fig.4 Uniaxial experimental stress-strain curves

由圖4 可知,巖石單軸強度存在明顯的尺寸效應。在一定尺寸范圍內,巖石單軸強度隨試件體積和高徑比增大而減小。在巖石尺寸效應現象上,學者們各執一詞。有學者認為巖石尺寸效應現象主要源于實驗過程中端部效應,當采用減摩手段和數值模擬研究時,將不會觀察到尺寸效應現象[7-8]。但隨著測試設備精密化發展和數值模擬軟件更新優化,越來越多學者認為端部效應存在一定局限性,端部效應只能影響高徑比小或體積小巖石,對于高徑比大或體積大巖石,端部效應的影響可以忽略,巖石尺寸效應主要由巖石非均質性造成。試驗采用理論模型分析巖石尺寸效應現象。巖石形狀效應中,以10 個標準試件為基準試件,通過計算標準試件強度離散系數得出巖石均質度m為2.51;而在巖石體積效應中,以b-1 試件為基準試件計算出巖石形狀效應中巖石均質度m為10.98。從理論上分析,巖石形狀效應與體積效應中試件均取自同一母巖,均質度應一致,但計算結果卻呈現不同的結果。究其原因,形狀效應中基準試件為?50 mm×100 mm,體積效應中基準試件為?20 mm×20 mm。體積越大巖石中所包含微空隙等缺陷越多,同時標準試件高徑比為2 受端部效應限制作用更小,造成形狀效應中巖石均質度要大于體積效應。但隨著基準試件數量提高,兩者均質度會趨于一致。根據巖石均質度和基準試件體積,得出Weibull 分布下巖石尺寸效應理論表達式。

(1)形狀效應。

式中,ν為形狀效應中試件體積,m3;ν0為標準試件參考體積,m3。

(2)體積效應。

式中,ν為體積效應中試件體積,m3;ν0為b-1 試件參考體積,m3。

同理,得出對數正態分布下巖石尺寸效應理論模型。2 種理論模型與實驗室強度結果如圖5所示。

圖5 單軸壓縮實驗結果與理論模型對比Fig.5 Comparison between experimental results and theoretical models in uniaxial compression

由圖5和表2、表3 誤差分析可知,Weibull 分布理論模型誤差較小,與試驗結果更為相符;受端部效應的影響,形狀效應中的誤差要大于體積效應中誤差;靠近基準試件誤差較小,遠離基準試件誤差較大。結合上述分析,取體積效應中均質度更為合適。

表2 形狀效應中理論模型與試驗結果誤差分析Table 2 Error analysis of theoretical model and experimental results in shape effect

表3 體積效應中理論模型與試驗結果誤差分析Table 3 Error analysis of theoretical model and experimental results in volume effect

2.3.2 分形維數與試件強度關系分析

在巖石尺寸效應研究中,巖石被認為是非均質材料,其內部分布著大量雜亂無章微裂紋和微空隙,導致其力學行為存在很大離散性。這就導致了現有的連續介質理論和離散性介質理論(巖石為結晶材料)均不能較好地解釋這種材料[9]。分形幾何能有效并定量地描述巖石中裂紋分布,有文獻[10]指出,巖石破裂發生在一個分維空間中,其分維值是巖石內部結構、變形過程和試件幾何形狀的綜合體現,分形幾何為巖石強度尺寸效應提供了新的分析工具。分維數是分形幾何中核心概念,一方面,分維數有著明確的物理含義,如零維的點、一維的線、二維的面、三維的體等諸如此類。另一方面,分維數是一個抽象的概念,如英國海岸線分維數為1.26,介于1 ～2 之間,又如當一塊海綿在不受壓時,其占據一定體積,此時它的歐氏維數為3,當受到較大壓力時可以看作2 維,所以受壓海綿分維數介于2 ～3 之間。分形幾何理論給出了分維數的計算方式:

式中,D為分形維數;a、b物理含義為一個圖形被放大a倍后,其占有長度(面積或體積)比原先增大b倍。

采用圖像二值化處理巖石破碎形態圖,圖中各個像素點是由3 原色組成的,RGB為三原色紅(R)、綠(G)、藍(B)3 個顏色通道的變化以及它們相互之間的疊加來得到各式各樣的顏色。RGB最高為255,呈白色;最低為0,呈黑色。根據3 原色直方分布圖選擇閾值,當大于閾值時RGB為255,小于時RGB為0。處理流程如圖6所示。

圖6 圖像二值化處理Fig.6 Image binarization processing

采用盒計數方法計算每個試件破壞后裂紋分形維數。所謂盒計數法指的是用邊長為N的網格紙覆蓋在裂隙上,計算裂隙所占的網格數M,在將N和M繪制于對數坐標軸中,采用線性擬合得出裂紋的分形維數。分形幾何理論指出,對于同一種工況下巖石破壞裂紋的分形維數應該是一定值。由于圓柱試件是一個曲面物體,所以二值化中圖像僅中間一部分可以看作為平面裂紋,對每個試件取5 處裂紋分布方向計算分維值,選用Matlab 科學軟件編碼計算出各個試件平均分形維值。由于a-1 組試件破碎程度高,無法拍照取樣。選取巖石形狀效應中a-2～a-7 組,巖石體積效應中b-1～b-5 組試件進行分析,各個試件的分維數如圖7所示。

圖7 試件裂紋分布分維數Fig.7 Fractal dimension of crack distribution in the specimen

與混凝土試件有別,巖石破壞的裂紋分布分維數隨著體積增加呈減少趨勢[11]。巖石尺寸越大,其裂紋越清晰、細化,從直觀感受中也可得出相似的結論。文獻[12]給出了分維數與立方體混凝土試件經驗公式,在此基礎上,假定巖石尺寸效應經驗公式中巖石分維數與強度滿足于下列關系:

式中,A、B為待定參數;d為各個工況下巖石裂紋分布分形維數。

經驗公式與巖石尺寸效應實驗結果擬合關系如圖8所示。

圖8 分形維數與強度關系Fig.8 Relationship between fractal dimension and intensity

由圖8 知,巖石裂紋分形維數與強度之間存在良好的關系,由分形維數得出強度的經驗公式具有一定的合理性。

2.3.3 聲發射信號規律分析

巖石聲發射技術(AE)主要應用于監測采集巖石破壞過程中聲信號變化,通過對聲信號趨勢的分析,監測變形破壞時特征,有利于揭示尺寸效應的內在機理。由于聲發射參數類型多樣且趨勢大多一致,故選取事件計數和累計聲發射計數2 個代表參數作為主要的分析對象。通過1 個或幾個撞擊鑒別出來的聲發射事件個數,可以反映出聲發射活動的總量和頻度。以形狀效應試件為例,聲發射信號如圖9所示。

圖9 形狀效應中巖樣聲發射計數Fig.9 Acoustic emission counting of rock samples in shape effect

由圖9 知,當壓力機開始加載時,巖石試件中原生微裂紋開始受力閉合,顆粒間受力摩擦滑動產生少量的聲發射信號。應力應變曲線中的孔隙壓密階段可以視為聲發射計數的相對活躍階段。高徑比為0.4、1、1.5、2、3、4、5 的巖石現階段累計的聲發射計數分別為4 319、5 720、6 486、2 527、9 952、4 956和13 662 次。大致規律為巖樣高徑比越大,其巖樣內部初始裂隙含量越多,初始微裂紋壓實過程中釋放的聲發射信號越多。隨著軸向應力應變進入到彈性階段,此時聲發射信號較少主要來自于初始裂紋的進一步壓密,可以看作為聲發射信號的平靜期。此階段,軸向應力不足以迫使巖樣產生新的微裂紋,巖樣處于彈性變形。當軸向應力超過巖樣屈服應力時,巖樣聲發射信號大量釋放,表現為聲發射計數顯著增加和累計聲發射計數呈快速增長的趨勢,為聲發射信號活動期。此階段中,巖樣內部裂紋突然滑移,產生更多微裂紋,微裂紋互相連通和擴展形成宏觀裂紋造成巖樣的破壞。此時,高徑比為0.4、1、1.5、2、3、4、5 的巖石峰值聲發射計數分別為1 652、1 753、1 812、2 015、2 223、2 546、3 003 次。說明高徑比越大,峰值聲發射計數越大。由圖10 知,巖樣體積與峰值點聲發射計數為顯著線性關系,其中R2=0.974 1、0.940 5,擬合關系良好。究其原因,主要是與巖樣的破壞方式有關。體積越大的巖樣在壓縮過程中所需行程越大,儲存在壓力機中彈性能越大。故達到峰值強度時,壓力機中的彈性能突然釋放造成巖樣迅速崩解。所以高徑比大的巖石的破壞方式一般都伴有巨響和巖樣崩飛,從而造成高徑比大的巖石峰值聲發射計數越大。另一個原因是體積大的試件一般在峰值強度時快速形成較大的破壞面,而體積小的試件破壞面一般呈遞進式破壞至峰值點時完全破壞。所以小體積試件聲發射計數表現為小而分散,大體積試件表現為大而集中。

圖10 巖石聲發射計數尺寸效應規律Fig.10 Size effect law of rock acoustic emission counts

3 礦柱尺寸優化

3.1 工程背景

某金礦位于黔西南自治州貞豐縣,地處云貴川丘陵地區,海拔1 300 m 左右,地勢較為平緩。主要礦體呈多層緩傾斜薄礦脈產出,根據礦體薄和緩傾斜的兩個特點,現礦山采用淺孔房柱法和全面法,用人工假柱代替個別礦柱,以提高回采率。

3.2 礦柱應力與強度確定

3.2.1 礦柱應力確定

采用面積分擔法確定試驗采場中礦柱中應力,對于規則礦柱可直接采用公式計算,對于不規則礦柱可先采用Voronoi 圖解法劃分出每個礦柱承擔的面積,再利用公式計算。

式中,σpa為礦柱中應力,MPa;γ為上覆巖層容重,kN/m3;wp為方形礦柱寬度,m;wo為礦房寬度,m;z為試驗采場埋深,m。

對試驗采場采用Voronoi 法計算出各個礦柱承載面積如圖11所示。

圖11 Voronoi 法劃分礦柱承載面積Fig.11 Bearing area of ore pilcar divided by Voronoi method

3.2.2 礦柱強度確定

從上述研究中可以看出,巖石強度存在明顯的尺寸效應,但上述規律不能直接應用于礦柱尺寸的設計。原因是上述對巖石尺寸影響規律的研究都是基于巖石材料,而沒有考慮節理和裂隙等缺陷的影響。由于各種構造作用的影響,礦柱中含有大量的結構面,這些結構面使得礦柱表現為巖體的力學性質。所以從理論分析的方法設計礦柱尺寸存在一定的限制性。礦柱強度的經驗公式可以有效地解決這一問題。一般來說,經驗公式主要來源于大量樣本數據,沒有完整的推導過程。這只是一個近似表達式。然而,經驗公式充分考慮了各種影響因素的結果,更易于工程應用。如果能兼顧這2 個優點,礦柱強度公式將更適合采礦生產。

在Galvin 經驗公式[13]中,考慮了礦柱的形狀和體積的影響,并通過大量現場數據驗證其準確性較高。選取Galvin 經驗公式作為本次研究對象。

式中,Rp為礦柱強度,MPa;w為礦柱寬度,m;h為礦柱高度,m;v為礦柱體積,m3;a、b為擬合參數;R0為巖石強度,MPa。

上述研究中發現某金礦礦巖更符合Weibull 分布強度模型,將第1 節中尺寸效應理論公式改為概率形式。

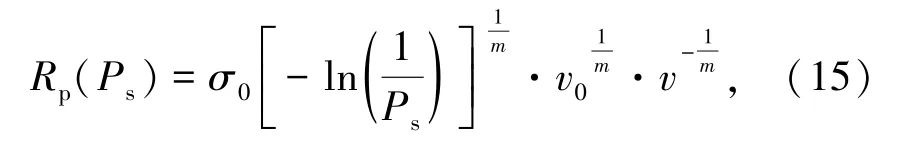
式中,Ps為礦柱穩定概率;Rp為穩定概率為Ps時礦柱強度,MPa。

綜合式(14)和式(15),結合Cheikhanoui[14-15]研究發現,Galvin 經驗公式參數與均質度m存在函數關系:

可得改進的礦柱強度經驗公式為

與原礦柱強度經驗公式相比,改進后的經驗公式考慮了礦柱的形狀效應和體積效應,并引入破壞概率和均質度m,所計算的結果更具有信服力且不失一般性。

礦柱安全系數計算為

Sjoberg 礦柱強度經驗公式被廣泛地應用于硬巖礦山,其礦柱安全表達式為

通過式(18)、式(19)計算出試驗采場各個礦柱安全系數如表4所示。

表4 試驗采場內礦柱安全系數Table 4 Safety factor of pillar in test stope

通過表4 可知,本研究所改進礦柱強度經驗公式較Sjoberg 公式所計算出來的安全系數偏小,當本研究公式綜合了礦柱強度經驗公式和理論公式的優點,所計算出結果更具有信服力。根據房柱法取值建議和現場考察,建議礦柱安全系數取值為1.3。根據安全性系數的結果,礦柱2和礦柱6 需要留意觀察;其他礦柱可根據現場實際情況決定是否回收。

4 結 論

(1)對2 種常用的尺寸效應理論模型進行了分析。歸納出Weibull 分布和對數正態分布下巖石尺寸效應理論公式。

(2)巖樣單軸抗壓強度隨巖樣高徑比的增大或放大系數的增加而減小,表現為明顯的尺寸效應,強度衰減規律與Weibull 分布更為相符。

(3)巖石尺寸越大,其裂紋越清晰、細化。裂紋分形維數隨體積增加呈減小趨勢,基于混凝土試件強度與分形維數關系,分析出巖石強度與分形維數之間關系也滿足混凝土經驗公式;聲發射信號隨試件高徑比和放大系數的增加呈線性增加趨勢,小體積試件聲發射活動表現為小而分散;大體積試件表現為大而集中。

(4)基于礦柱強度經驗公式,結合巖石尺寸效應理論模型和試驗規律,改進了礦柱強度經驗公式。改進的礦柱強度經驗公式考慮礦柱形狀效應和體積效應,并引入破壞概率,可信度更高。