基于改進經驗小波變換的橋梁模態參數識別
秦世強,唐 劍,馮嘉誠
(武漢理工大學 土木工程與建筑學院,湖北 武漢 430070)
0 引言
結構模態參數包括頻率、阻尼比和模態振型,是結構最基本的動力參數。對橋梁健康監測而言,準確地獲取結構模態參數有著重要意義[1]。結構振動產生的信號一般都是非平穩信號,目前處理非平穩信號的方法主要有短時傅里葉變換、經驗模態分解(Empirical Mode Decomposition, EMD)、小波變換、經驗小波變換(Empirical Wavelet Transform, EWT)等。其中,短時傅里葉變換能分析非平穩信號,但是窗函數一旦選擇就固定,這使得短時傅里葉變換時頻分辨率受海森堡測不準原理的限制[2];小波變換通過設置不同的尺度因子和平移因子對小波函數進行伸縮和平移,構建出具有不同分辨率的小波濾波器組,從而使小波變換具有多分辨率的特性,因此小波變換可以由粗及細地逐步分析信號,然而,小波變換需要人為設置小波基,因此缺乏自適應性[3];經驗模態分解能夠自適應地將信號分解為若干個單頻率成分的信號分量,結合Hilbert變換可獲得信號的時頻分布,然而,經驗模態分解法存在欠包絡、過包絡、模態混疊、端點效應、沒有嚴謹的理論背景等問題[4]。經驗小波變換是Gilles[5]在2013年提出的一種新的自適應信號處理方法,該方法通過對頻譜進行自適應地劃分,并建立一組小波濾波器組,對信號進行濾波,將信號分解為一系列具有特定頻帶的本征模態函數。EWT兼顧小波變換的理論背景和經驗模態分解的自適應性,因此在處理平穩和非平穩信號方面具有巨大的優勢。目前,EWT已經在機械、電氣、土木等領域得到了廣泛的應用。向玲等[6]將EWT應用于旋轉機械故障診斷,并將EWT與EMD結果進行了對比,結果表明EWT分解得到的故障頻率成分多于EMD,且能避免EMD模態混疊、端點效應、計算量大等缺點,為機械故障診斷提供一種新思路。Liu等[7]將經驗小波變換應用于地震時頻分析,利用該方法對仿真、二維和三維實際數據進行分析,驗證了EWT在描述地層特征和構造特征方面優于傳統小波變換。陳浩等[8]將EWT結合能量型頻率主成分提取方法提出一種脈沖雷達實時加速度估計方法,仿真和理論數據分析結果表明新的方法較之于傳統方法精度更高、計算速度更快。趙妙穎等[9]將EWT用于變壓器振動信號特征提取,通過計算子分量與原始信號的相關系數,并提取相關度高的分量,該方法能在去除包含較弱特性信息分量的同時達到降低維度的目的,有效減少了計算量。夏雄等[10]利用EWT識別橋梁結構模態參數,通過仿真信號和斜拉橋模型試驗測試數據驗證了EWT對于信號分解的有效性和模態識別的可行性。
然而,傳統的EWT算法存在很多問題,如采用局部極大值、局部極小值的方法進行頻譜分割容易受到噪聲的干擾,從而影響信號分解結果;對于擁有共振邊頻帶的信號在高幅值邊頻帶位置這兩種方法會過多的劃分,使得同一個子分量分解到不同的分量中,而低幅值的邊頻帶得不到劃分,造成頻帶劃分不合理;而采用尺度空間法分解得到的分量過多,產生了許多虛假的分量,且隨著信號復雜度的增長尺度空間法運行時間將會變得很長。針對EWT以上問題,目前的改進方法可以分為4類;(1)更換抗噪能力強的頻譜代替傅里葉譜進行頻譜分割。劉自然等[11]采用閾值修整后的傅里葉譜包絡曲線來確定邊界,與傳統EWT相比該改進方法更精確地提取與故障相關的信號時頻特征,在低信噪比情況下魯棒性好。Hu Y等[12]提出采用基于順序統計濾波器的包絡方法尋找主要頻譜峰值,提出3個準則來篩選有用平頂,以確定EWT所需的邊界。萬熹等[13]利用burg算法估算出的自回歸功率譜代替傅里葉譜進行頻譜分割,該頻譜對于高噪聲或低信噪比的數據有著高分辨率頻譜估計。(2)優化邊界。Dong S等[14]提出局部窗極大值分割算法確定經驗小波變換所需要的頻帶邊界,結合邊界優化算法壓縮頻帶帶寬,降低分解后子分量噪聲水平。(3)篩選感興趣的分量。Qiao Z等[15]采用尺度空間法確定EWT的邊界,利用互信息合并相鄰相關分量,故障信號分析結果表明,該方法不僅能有效地減少故障信號的分量,而且能從復雜信號中提取出故障信號成分。郭輝等[16]采用尺度空間法劃分頻譜,并對峭度值大于閾值的分量作相關性分析,合并相關性高的分量,對合并后的分量進行包絡分析,提取故障沖擊。(4)對原始信號或者分解后的子分量去噪。李政等[17]提出最大相關峭度解卷積降噪與改進 EWT相結合的滾動軸承早期故障識別方法,試驗結果表明新方法能有效降噪、增強信號中周期性沖擊特征、實現滾動軸承早期微弱故障的識別。然而對于第1類改進方法同樣還是存在許多的不足,例如采用AR功率譜確定邊界時AR模型的定階一直是難題,目前的定階方法計算出來的階數并不一定是最佳的模型階次;確定信號傅里葉包絡譜時往往要進行多次包絡才能得到最佳包絡,最佳包絡次數往往是不確定的;采用順序統計濾波器確定的上包絡譜改進時,窗口寬度設定是一個問題,同時有效平頂的選擇較為復雜;其他頻譜在計算過程中同樣存在計算困難,參數設置復雜等問題。為解決上述問題,本研究提出一種改進的EWT(Improved EWT, IEWT);IEWT采用在低信噪比的條件下比傅里葉譜更光滑的EWT趨勢譜進行頻譜分割,相比于其他頻譜,EWT趨勢譜構造簡單,原理與經驗小波變換相同且不涉及其他理論;同時,為消除信號子分量中存在的噪聲,進一步引入同步提取變換(Sychroextracting Transform, SET)對分解的信號子分量去噪,提高模態參數識別精度。論文通過仿真信號驗證IEWT的頻譜劃分效果,并以Dowlinghall橋為工程案例,結合隨機減量技術(Random Decrement Technique, RDT)與Hilbert變換識別其模態參數,考察IEWT識別模態參數的精度及在不同噪聲水平下的魯棒性。
1 經驗小波變換
1.1 頻譜劃分
EWT通過對頻譜進行分割,并建立一組小波濾波器,對信號進行濾波,將信號分解為一系列具有特定頻帶的本征模態函數,因此,頻譜分割是經驗小波變換的核心步驟,頻譜分割將影響小波分解的精度。首先,對信號進行快速傅里葉變換;然后,將傅里葉譜的頻率范圍規范化為[0,π],并檢測規范化頻譜中的所有極大值點以及對應的頻率;最后,將所有極大值點進行排序,假設極大值個數為M,經驗小波變換分解的模態分量數設為N,此時除了0與π兩個邊界外,還需要確定N-1個邊界,因此存在以下兩種情況:
情況1:M≥N,此時該方法搜索到足夠多的極大值,保留前N個極大值。
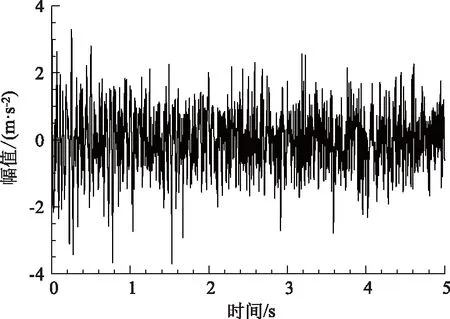
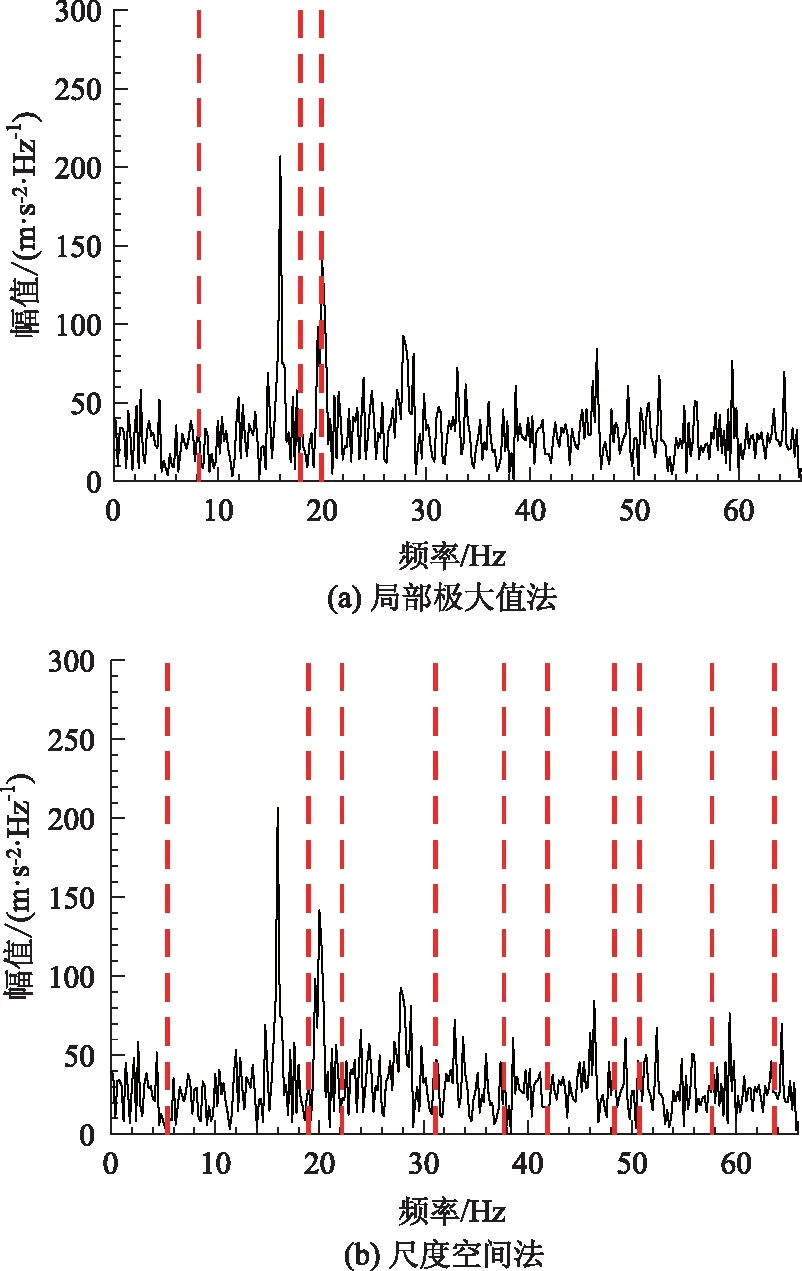
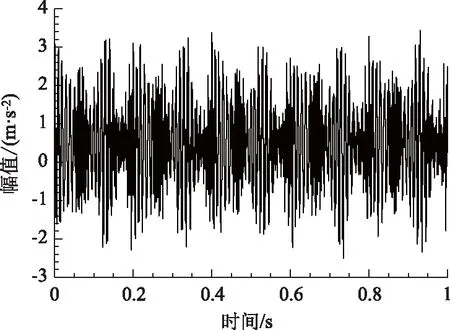
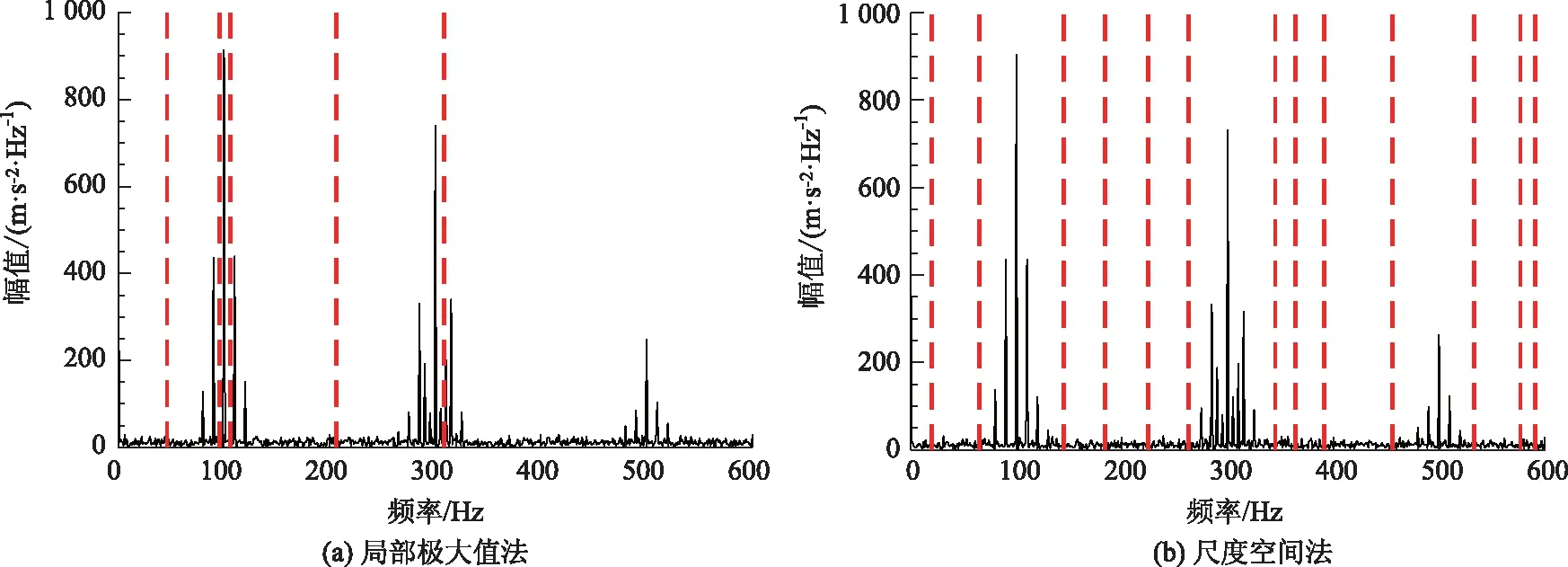
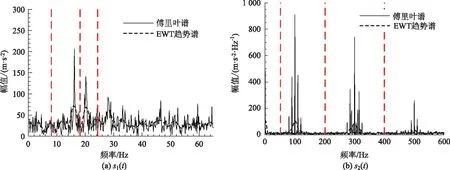
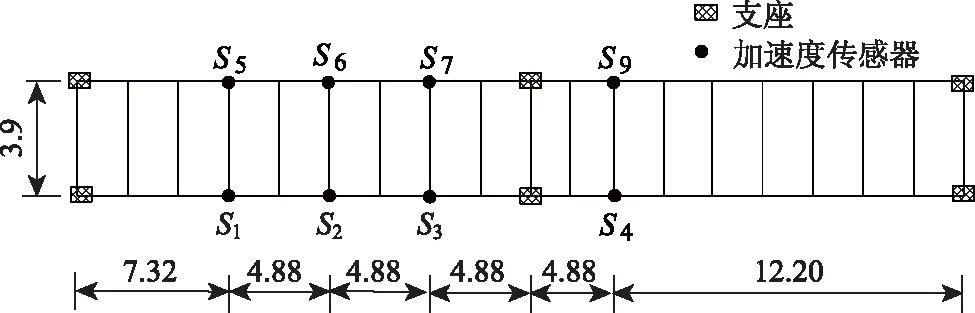
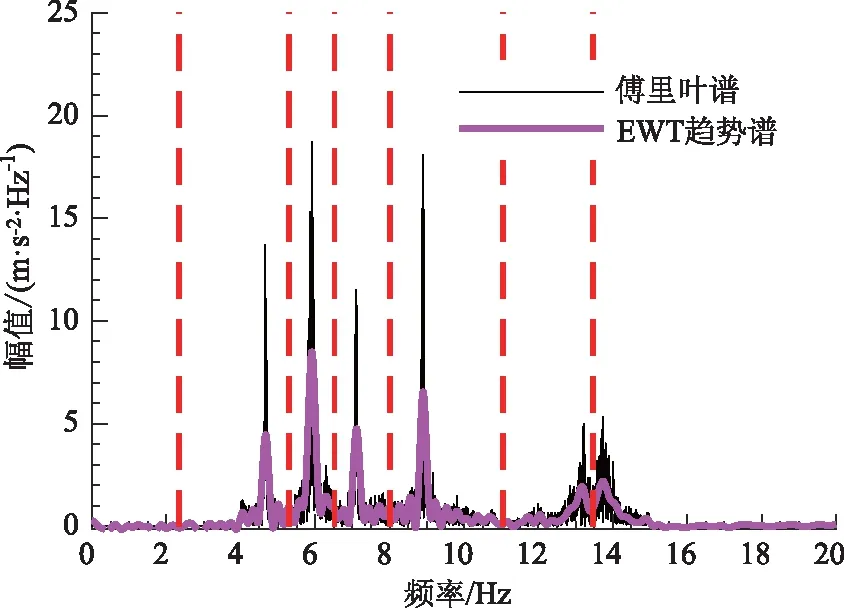
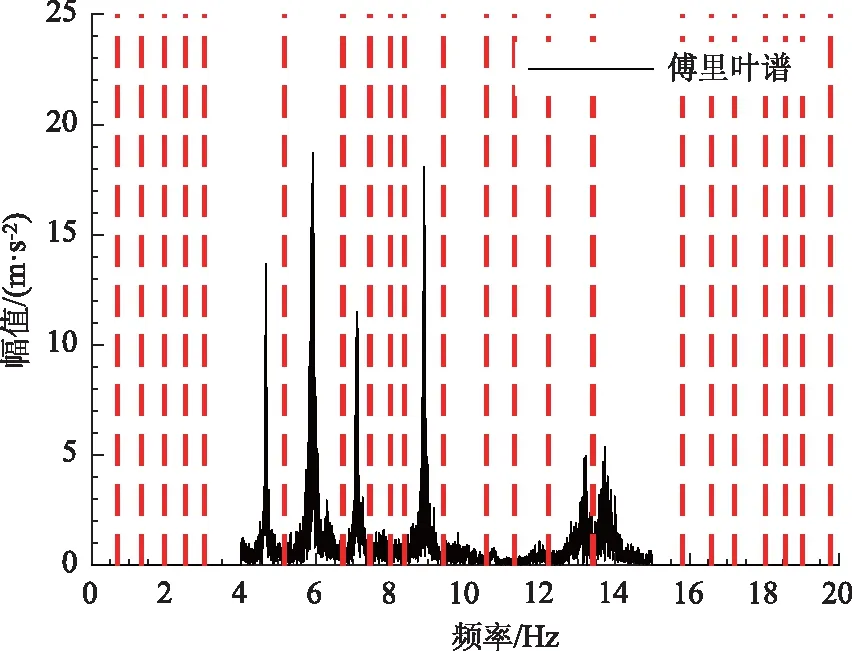
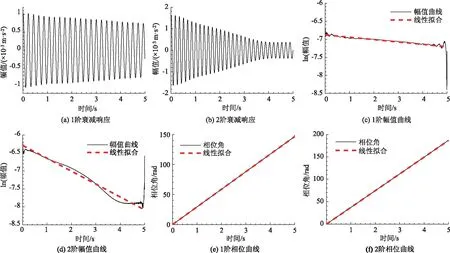
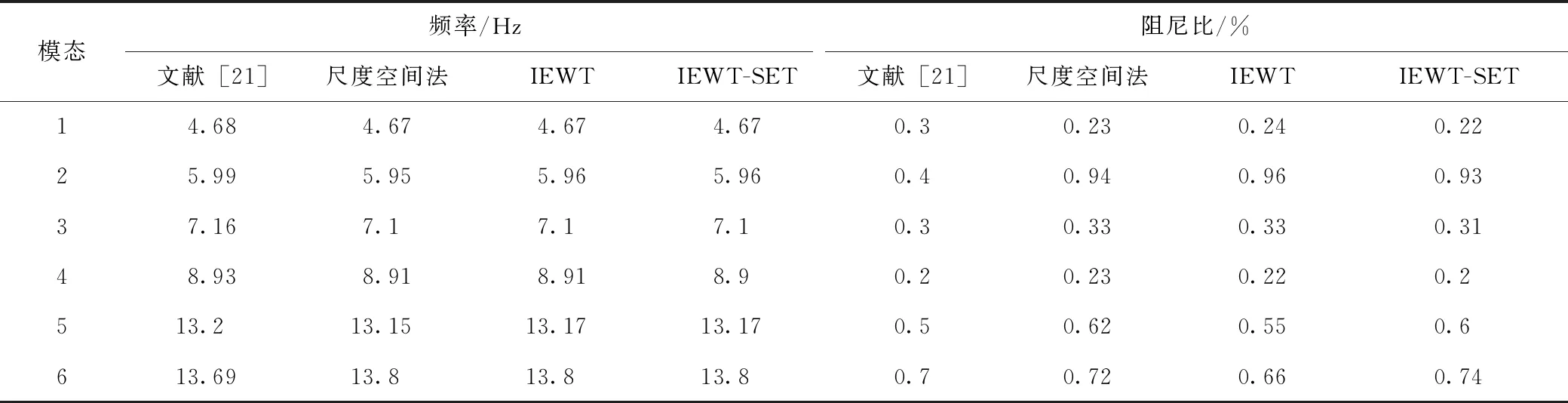
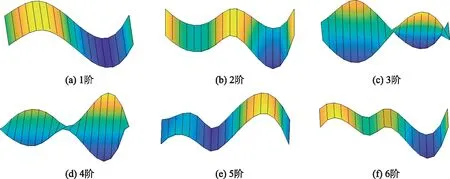
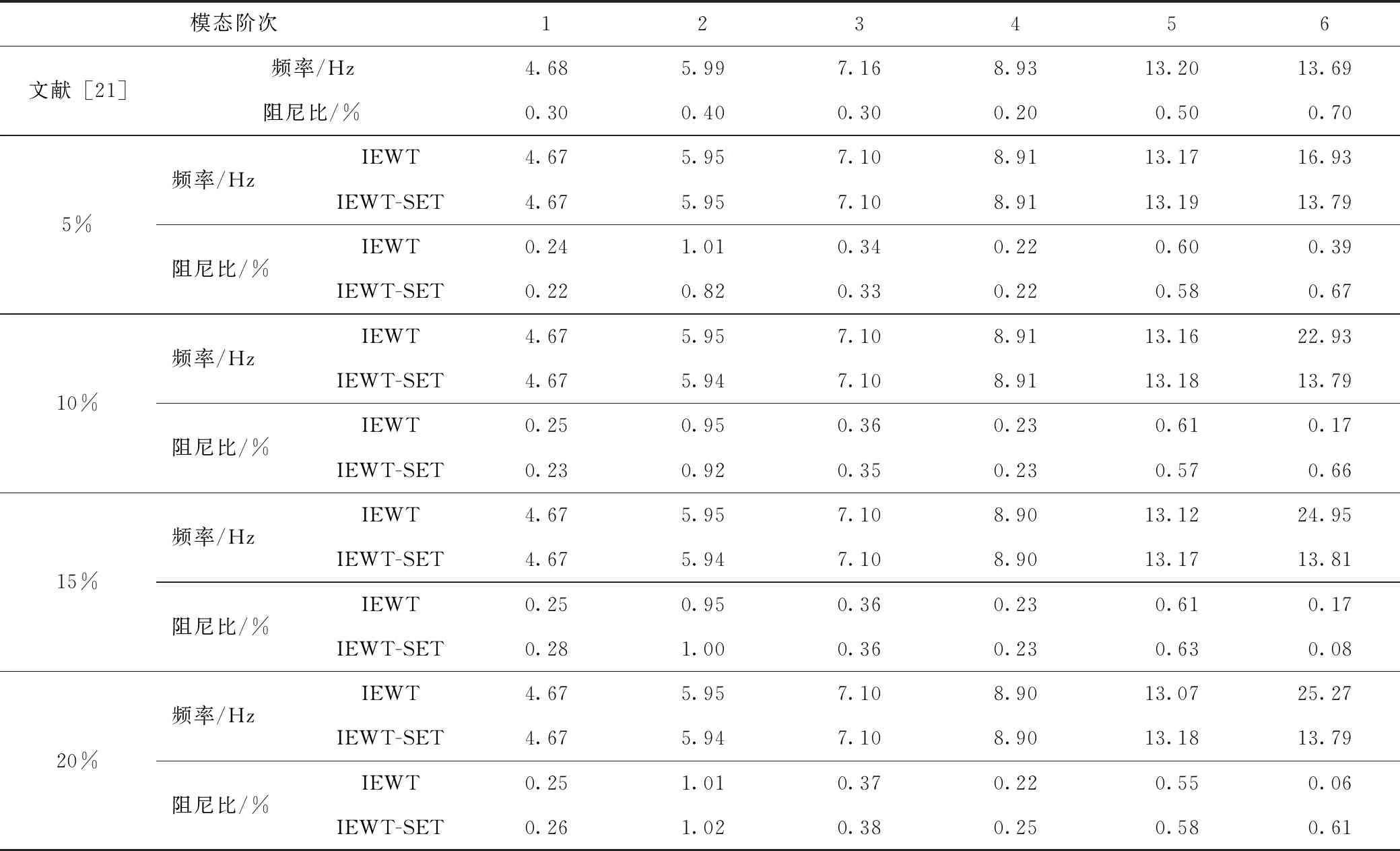
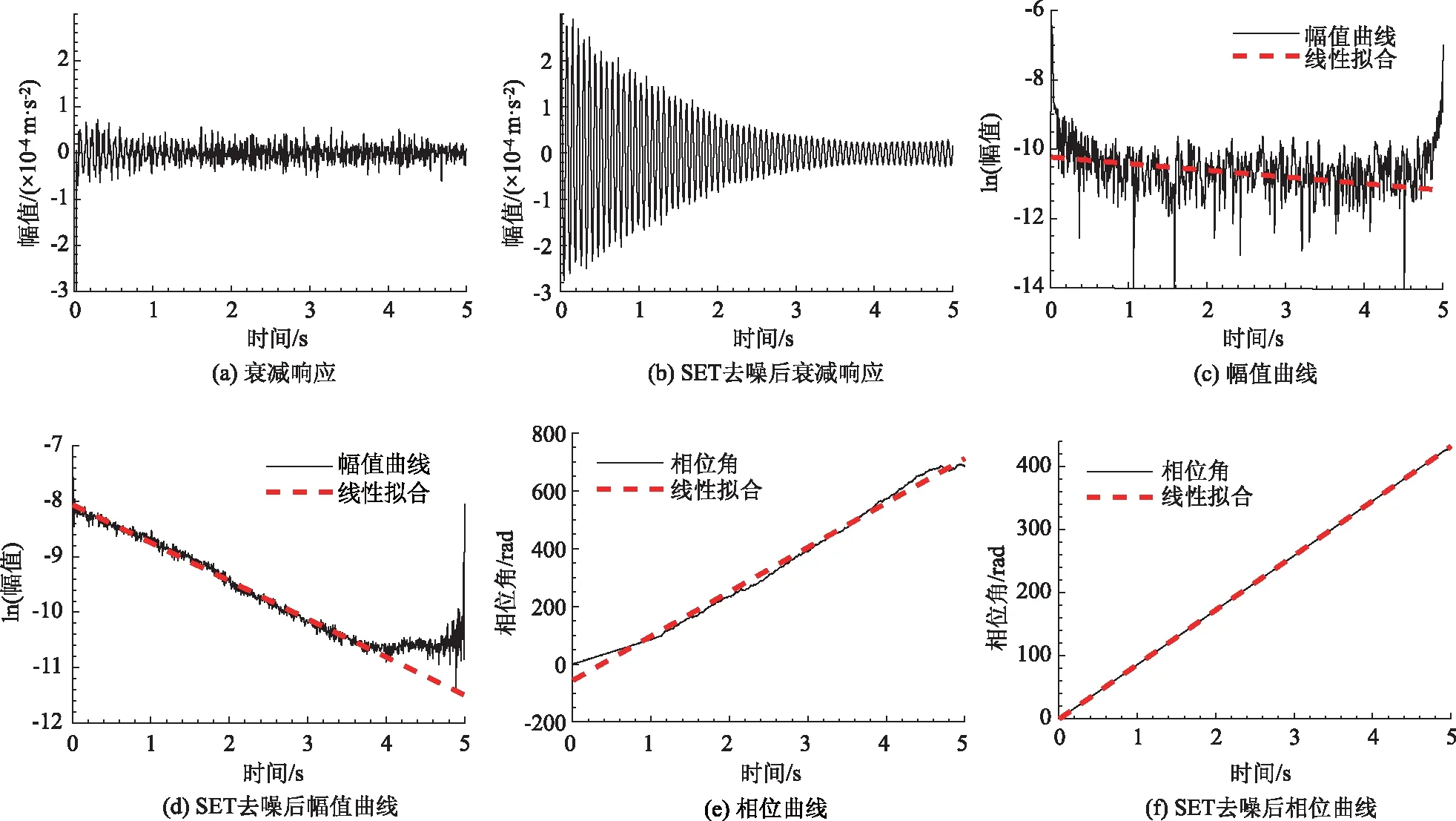
情況2:M 通過對規范化的頻譜進行頻譜分割,將頻率范圍為[0,π]的頻譜分割為N個連續區間Λn=[ωn-1,ωn](其中n=1,2,…,N且ω0=0,ωN=π)),以ωn為中心,設置帶寬為2τn的過渡帶,其中τn=γωn,γ為系數。頻譜分界如圖1所示。 圖1 頻譜分界示意圖 (1) (2) (3) (4) (5) 經驗模態fk(t)定義如下: (6) 經驗小波變換頻譜劃分的常用方法一般為局部極大值法、局部極小值法、尺度空間法。局部極大值法、局部極小值法進行頻譜分割容易受到噪聲的干擾,從而影響信號分解結果。對于擁有共振邊頻帶的信號,在高幅值邊頻帶位置這兩種方法會過多地劃分,使得同一個子分量分解到不同的分量中,造成頻帶破裂;低幅值的邊頻帶得不到劃分,造成頻帶劃分不合理。ε鄰域法需要人工設置初始邊界,不具有自適應性,且最終頻譜分割結果依賴設置的初始邊界,采用局部極大值或者局部極小值設定初始邊界時,也存在著兩種方法具有的缺陷。尺度空間法得到的邊界過多,產生了許多虛假的分量,隨著信號長度的增加,尺度空間法運行時間將會變得很長。環境激勵下結構的振動受到環境噪聲的影響,使得振動信號傅里葉譜存在較多的噪聲干擾。同時,快速傅里葉變換算法中補0和截0的措施往往會導致信號失真和頻譜泄露等問題,使得振動信號傅里葉譜具有邊頻帶,即除了在固有頻率處出現頻譜峰值外,與之接近的頻率范圍內也具有較大的峰值。為了進一步驗證經典頻譜分割存在的上述問題,通過仿真信號進行數值算例研究。 (1) 仿真信號 由16,20,28 Hz這3種頻率分量組成,假定采樣頻率為240 Hz,連續采樣5 s,通過在仿真信號添加高斯白噪聲以降低信噪比,使信噪比SNR達到-5.98 dB;該信號的時程曲線如圖2所示。 圖2 仿真信號s1(t)時域圖 (7) 由于仿真信號s1(t)存在3個分量,因此,采用局部極大值法進行頻譜分割時,設置的模態分量數N=4。局部極大值法、尺度空間法頻譜分割結果分別如圖3(a)~(b)所示。從圖3(a)可以看出:當在信號中添加了噪聲時,傅里葉頻譜圖在20 Hz左右的位置產生了由噪聲分量引起的峰值,其幅值比原信號中28 Hz的分量大;局部極大值法選取的頻譜峰值并非是28 Hz的分量產生的峰值,而是噪聲分量產生的峰值,因此得到的邊界并沒有將原信號的3個分量分離開。從圖3(b)可以看出:尺度空間法成功分離了原信號的3種頻率成分,但同時得到過多的頻率邊界,后續經驗小波變換時,將產生過多的虛假分量。 圖3 s1(t)傅里葉譜分割 (2) 仿真信號s2(t)由3個調頻-調幅信號組成,其中心頻率分別為100,300,500 Hz,調制的頻率分別為10,15,20 Hz為了使仿真信號更符合實際,在信號中加入均值為0方差為1的高斯白噪聲n(t)。仿真信號s2(t)的時程曲線如圖4所示。采樣頻率為2 000 Hz,采樣時間為1 s。 圖4 仿真信號s2(t)時域圖 (8) 由于仿真信號s2(t)存在3個分量;采用局部極大值法進行頻譜分割時設置的模態分量數N=6;局部極大值法、尺度空間法的頻譜分割結果分別如圖5(a)~(b)所示。由于分量1和分量2的頻譜幅值較大,利用局部極大值法進行頻譜分割時,檢測的邊界都集中在分量1和2中,出現了過分解現象;分量3的幅值較小導致在檢測局部極值時,即使對含有3個子分量的信號設置分解分量數N=6,分量3頻譜幅值峰值點都無法探測到,致使分量2和分量3未得到分離。尺度空間法雖然能將3個分量分離開且3個分量也未出現過分解和混疊的現象,但是在各個分量間劃分過多,導致最后分解結果出現虛假的分量,在分析分解后的分量時需要人工選擇有用的分量。 圖5 s2(t)傅里葉譜分割 針對上述問題,本研究采用趨勢譜代替傅里葉譜進行頻譜分割,提高頻譜分割精度。具體做法如下:(1)對信號的傅里葉譜進行快速傅里葉變換。(2)采用局部極大值法或者局部極小值法分割,分解的分量數設置為N(N>10)。(3)去除分解后的高頻分量,用剩余的分量(0.5~0.8N)重構頻譜。重構產生的EWT趨勢譜與原傅里葉譜具有高度的相似性,與傅里葉譜相比,趨勢譜在低信噪比和具有邊頻帶的條件下更光滑,因此,采用趨勢譜代替傅里葉譜進行頻譜分割能夠很好地分解染噪信號和具有邊頻帶的信號。 采用EWT趨勢譜s1(t)和s2(t)進行頻譜分割,其結果如圖6(a)~(b)所示。仿真信號s1(t)的傅里葉譜在20 Hz左右由于噪聲的影響產生了毛刺,采用局部極大值法搜索的邊界會有偏差,而從圖6 (a)看出EWT趨勢譜在20 Hz附近很光滑,因此在頻譜分割時能很好地將3階分量分離。具有邊頻帶的信號s2(t)的EWT趨勢譜也很光滑,并且不存在邊頻帶,采用局部極大值法探測邊界時,僅設置N=4就可以將3個子分量完整分離開來,而利用傅里葉譜結合局部極大值法確定邊界設置分量數N=6在分量2和分量3之間仍未探測到邊界。 圖6 s1(t)和s2(t) EWT趨勢譜分割 上述仿真信號的研究結果表明:相較于傅里葉譜,采用EWT趨勢譜來確定經驗小波變換的邊界精度更高,在低信噪比的條件下也表現良好,并且能避免邊頻帶對頻譜劃分的干擾。 使用EWT趨勢譜代替傅里葉譜進行頻譜分割,可以減少噪聲和其他干擾對頻譜分割的影響,但是這種方法并沒有去除原始信號中的噪聲。信號分解后的各個子分量中仍然存在噪聲和部分的混疊,這影響著模態參數識別結果。為此,論文引入同步提取變換[18]進一步處理單分量信號,以降低噪聲和混疊對模態參數識別的影響。同步提取變換僅保留時頻脊位置的時頻系數,其余位置時頻系數置0,以達到去除噪聲、提高信號信噪比的目的。離散的多分量信號表達式為s(t)=Ae-iω0t,式中,A為幅值;i為虛數單位;ω0為固有頻率;對該信號做短時傅里葉變換可獲得信號的時頻譜G(t,ω),即: (9) T(t,ω)=Ge(t,ω)δ(ω-ω0(t,ω)), (10) (11) 式中,Aj(t),φj(t)分別為第j階信號分量的幅值函數和相位函數;m為信號的分量數。通過新的時頻譜可獲得各階分量的時頻脊,進而利用時頻脊將原始信號所包含的子分量重建出來。該信號可以重構為: (12) 隨機減量技術[20]是一種提取環境激勵下結構振動響應自由衰減響應的方法。該方法利用平穩隨機響應平均值為0的特性,對原始信號中的確定性分量和隨機分量進行辨別,將確定性分量從原始信號中分離出來,得到自由衰減響應。 隨機減量技術主要通過選取一個適當的常數A去截取該系統的振動響應信號y(t),可得到一系列不同的交點時刻ti,對以ti時刻后為起點的一系列子振動響應取統計平均值,可得到以常數A為初始振幅的自由衰減振動響應信號x(t)=AD(t),式中D(t)為幅值為1的自由振動響應。 對由隨機減量獲得的第j階自由衰減響應進行Hilbert變換,可獲得幅值曲線Uj和相位曲線θj(t),即: (13) 式中,Uj為瞬時幅值;ξj為阻尼比;ωnj為固有頻率;ωdj為阻尼頻率;αj為初始相位。 對希爾伯特變換獲得的幅值曲線取對數,可以作出幅值對數曲線,進而擬合幅值對數曲線和相位曲線,并且求擬合直線的斜率,可以計算出第j階頻率ωnj和阻尼比ξj,即: (14) 對于第j階模態,結構上任意兩點p,q振型分量(φjp,φjq)由式(15)決定;其符號由式(16)決定,當相位差為±2mπ時,兩者同號;當相位差為±(2m+1)π時,兩者異號。 |φjp|/|φjq|=e[Ljp(t)-Ljq(t)], (15) (16) 式中,t0為響應的任意時刻;θjp,q為p,q兩點在該時刻的相位差;Ljp(t),Ljq(t)分別為p,q兩點幅值對數曲線的擬合直線;θjp(t),θjq(t)為p,q兩點相位曲線的擬合直線。以同一點為參考點可以確定該模態其他點的振型分量大小和符號,由此可得第j振型φj。 φj=[φj1,φj2,…,φjn]T。 (17) 以上內容介紹了從橋梁振動響應信號中獲取模態參數各個步驟的原理,現將改進經驗小波變換、同步提取變換、隨機減量技術、希爾伯特變換結合起來,得到基于改進經驗小波變換的模態參數識別方法,整個操作流程總結如下: 步驟1:將振動信號x(t)進行快速傅里葉變換獲得傅里葉譜。 步驟2:對傅里葉譜進行經驗小波變換,采用局部極大值法進行分割,分解分量數為N(N>10),去除高頻分量,用前0.5~0.8N項低頻子分量進行頻譜重構。 步驟3:利用重構的EWT趨勢譜,采用局部極大值法進行頻譜劃分,并建立濾波器組,對振動信號x(t)進行經驗小波變換。 步驟4:對各個信號子分量進行同步提取變換去噪。 步驟5:通過隨機減量技術對去噪后的分量進行處理,獲得自由衰減響應。 步驟6:將自由衰減響應進行希爾伯特變換,得到幅值曲線、相位曲線。 步驟7:采用最小二乘法擬合幅值曲線、相位曲線,得到擬合斜率,利用式(14)~(17),可求得頻率、阻尼比、振型。 基于改進EWT的橋梁模態參數識別流程如圖7所示。 圖7 基于改進EWT的橋梁模態參數識別流程圖 Dowling Hall橋[21]是兩跨連續鋼桁架梁橋,橋面板為鋼筋混凝土板。該橋位于美國Tufts大學,全長44 m,寬3.9 m。在2009年4月和6月進行了兩組預試驗,結果表明環境振動條件下水平振動比垂直測試的振動幅度小得多,且前6階模態主要集中于2~20 Hz之間,因此在正式試驗只收集各測點豎向加速度響應。自2010年1月5日至2010年5月2日,該橋進行了為期17周的持續監測。Dowling Hall橋上共布置了8個加速度傳感器,分別為S1,S2, …,S8,各個傳感器布置如圖8所示。各加速度傳感器只測試豎向加速度響應,在本次監測中,采樣頻率為2 048 Hz,每小時自動采集300 s的數據樣本。為了提升計算效率將測量數據從2 048 Hz重采樣到128 Hz,選擇2010年4月29日15:00時的監測數據進行模態分析。 圖8 加速度傳感器布置(單位:m) 對各個測點的數據進行[4 Hz,15 Hz]帶通濾波去除其中存在的噪聲的干擾。然后對濾波后的加速度時程進行分析,以1#測試點為例,濾波后其加速度時程如圖9所示。 圖9 1#點加速度時程 首先,對獲取的EWT趨勢譜采用局部極大值法檢測邊界,并建立小波濾波器組,對加速度響應進行濾波,得到6階模態對應的加速度分量;其次,采用隨機減量技術處理加速度分量,得到各階模態的自由衰減響應,關于隨機減量技術的參數設置,截取的閾值設為信號標準差的1.4倍,衰減長度為5 s。然后,利用希爾伯特變換可以得到各階自由衰減響應曲線幅值和相位隨時間的變化,即瞬時幅值和瞬時頻率;最后,分別對幅值對數曲線和相位曲線進行線性擬合,通過式(14)~(17)計算頻率、阻尼比和模態振型。EWT趨勢譜確定的邊界如圖10所示。原信號采用尺度空間法頻譜分割如圖11所示。圖12為EWT趨勢譜經驗小波變換前2階模態的自由衰減響應、幅值對數、相位圖。 圖10 趨勢譜分割 圖11 尺度空間法頻譜分割 圖12 前兩階模態自由衰減響應、幅值曲線、相位曲線 根據式(14)~(15)可求得頻率、阻尼比,其結果如表1所示。各階振型向量由式(16)~(17)計算得到,用MATLAB擬合各點畫出的振型圖如圖13所示。對比圖10和圖11可知:EWT趨勢譜能夠很好地反映出原傅里葉頻譜的變化趨勢,兩者的形狀也基本一致,對EWT趨勢譜進行N=7的局部極大值法頻譜分割,6階分量很好地分離開來;采用尺度空間法確定原傅里葉譜的邊界,雖然也能分離前6階模態,但是產生了多余的分量,進行模態識別時要事先判斷各階分量是否為有效模態,同時尺度空間法運行的時間太長,在很大程度上降低模態識別的效率。由表1兩種方法模態識別結果對比來看,采用IEWT,IEWT-SET(表示用SET對IEWT獲得的信號分量進行去噪)、尺度空間法識別出來的模態差別較小,說明了改進方法在高信噪比的條件下有著良好的模態識別能力,識別出來的模態精度較高。在識別過程中改進算法程序運行所需時間也比尺度空間法少且不需要對EWT分解的分量進行人工篩選。 表1 DowlingHall橋模態參數識別結果 圖13 Dowling Hall橋前6階振型 對各個測點的數據添加幅值為振動信號最大幅值5%,10%,15%,20%的噪聲以驗證改進方法在低信噪比條件下的魯棒性。對加噪后的加速度響應頻譜分割,進行經驗小波變換,對子分量作用同步提取變換去噪,結合隨機減量技術和Hilbert變換,可識別不同程度噪聲條件下的模態參數,其結果如表2所示。 表2 Dowling Hall橋加噪后模態參數識別結果 圖14為1#測試點在10%的噪聲條件下第6階模態SET去噪前后自由衰減、幅值對數擬合、相位擬合,很顯然去噪前自由衰減響應存在著大量噪聲,導致幅值對數圖和相位圖產生很大的偏差,而將第6階信號子分量SET去噪后的自由衰減響應曲線線型較為理想,幅值對數圖和相位圖擬合效果好。由表2可以看出,采用IEWT和IEWT-SET均能準確識別各個噪聲條件下前4階頻率,誤差較小。主要是因為在EWT分解后前4階分量雖然存在噪聲,但是噪聲強度并不大,采用隨機減量技術可以消除部分噪聲對模態識別的影響,因此前4階模態識別誤差不大。而噪聲主要分布在高頻區域,隨著噪聲強度的增加,第5階模態對應的振動信號分量噪聲水平增加,而隨機減量技術抵消噪聲干擾的能力有限,因此采用IEWT識別的頻率誤差也逐漸增大。第6階模態由于頻帶過寬導致原始信號加入噪聲對該模態對應的信號子分量信噪比影響很大,使得在加入5%的噪音時頻率的識別結果就產生了較大的偏差,而且隨著噪聲水平的增加這種偏差也越來越大。而采用IEWT-SET在各種噪聲條件下仍然能準確識別第5,6階模態,即使加入了20%的噪聲,頻率的識別結果精度仍能保持較高的精度。 圖14 第6階模態去噪前后自由衰減、幅值曲線、相位曲線 本研究針對經驗小波變換對于低信噪比和具有邊頻帶信號分解效果較差的缺陷,提出了一種基于EWT趨勢譜頻譜分割的改進的EWT方法,并結合SET去噪、RDT和Hilbert變換進行橋梁結構的模態參數識別。以兩個典型的仿真信號驗證采用EWT趨勢譜確定EWT邊界的可行性和有效性,并將該方法應用于Dowlinghall橋的模態參數識別驗證使用所提方法進行模態參數識別的準確性和魯棒性。可以得出以下結論: (1)EWT趨勢譜能準確地確定經驗小波變換所需要的邊界,即使對于低信噪比和具有邊頻帶的信號也表現良好。 (2)基于該改進方法識別環境振動條件下的結構頻率、阻尼比、振型是準確可靠的。該方法能有效地在低信噪比的條件下識別出結構的模態參數,是一種精度高、魯棒性好的結構模態參數識別技術。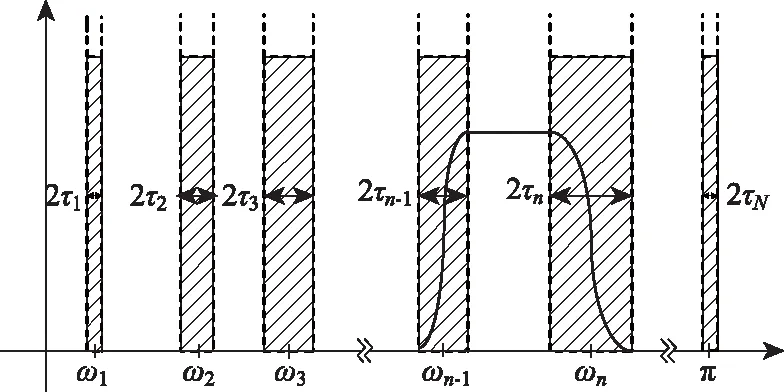
1.2 濾波器的建立
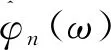
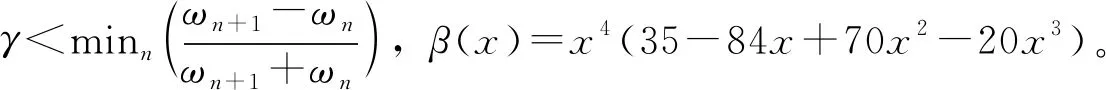
1.3 經驗小波變換
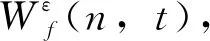
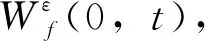
2 改進經驗小波變換
2.1 經驗小波變換的缺陷
2.2 EWT趨勢譜
3 基于改進經驗小波變換的橋梁模態識別
3.1 信號子分量去噪
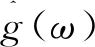
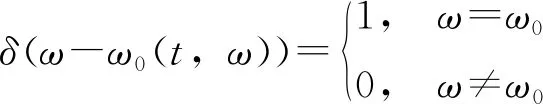
3.2 隨機減量技術
3.3 基于Hilbert的模態參數識別
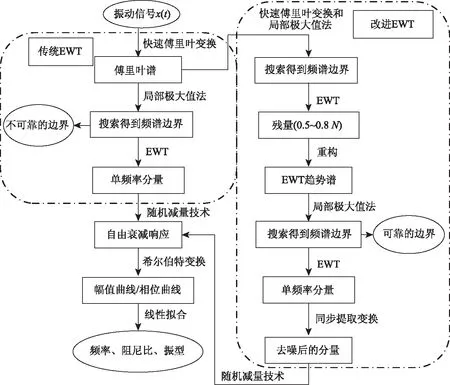
3.4 基于IEWT的橋梁模態參數識別步驟
4 工程案例
4.1 改進方法模態識別精度
4.2 改進方法在低信噪比條件下的魯棒性
5 結論

