基于線性代數矩陣理論的“學”與“用”

鄭前前，楊文杰，岳曉鵬

(許昌學院，河南 許昌 461000)

線性代數是高校理工科教育中一門重要的數學公共基礎課，是后續專業課程學習的基礎，能夠培養學生分析、解決問題的能力，提高學生的思維能力[1]。但在實際教學工作中，線性代數課程存在概念、理論較多，知識點彼此聯系不緊密，不能形成完整的知識結構，內容抽象不易被學生理解等問題[2-3]。以線性代數中線性相關性為例，大部分學生只能從定義上理解向量之間的關系，認為向量組線性相關或者線性無關，不能深層次理解、掌握其與解方程組之間的關系[4]，在矩陣理論的學習中也會遇到同樣的問題。線性代數是現代控制理論的基礎課程，也是其應用的一個重要方向，如系統最優化、系統可測及可觀等[5]。線性代數還是圖論及復雜網絡研究的重要工具，特別是特征值及特征向量[6]。線性代數與解析幾何也存在一定的關系[7]，但是這些聯系和承接關系，在線性代數課程學習過程中卻很少涉及。

線性代數作為一門基礎課程，不僅在學生學習過程中發揮著不可替代的作用，而且也是科研過程中重要的數學工具，如何在教學過程中發揮科研的作用是本文討論的重點。

1 基于矩陣理論的學與用融合

學與用融合是目前高校教學探索的主要模式，課程學習是學生創新及科研能力培養的前提，科學研究是基礎培養的主要目標之一，二者相輔相成，缺一不可。以矩陣理論與控制理論的融合為例，矩陣理論是線性代數中的主要學習內容，矩陣理論在應用數學與工程技術學科中都有著廣泛的應用。但是，線性代數課程中卻很少提及矩陣理論的應用，導致多數學生認為矩陣理論只能用于求解線性方程組，也不了解矩陣理論與后續課程之間的關系。以線性代數中矩陣理論的應用為出發點，在已有矩陣理論基礎上講授線性代數矩陣理論在微分方程求解問題及控制理論中的應用，使學生明確學習目標，激發學習興趣。

線性代數中矩陣理論主要應用于解線性方程組

即Ax=b解的問題。下面介紹矩陣理論的另外兩種應用：

在高等數學中，微分方程求解也是非常重要的問題，探討一階線性微分方程組[8]與矩陣理論之間的關系，一階線性微分方程組的一般表達式為

(1)

其中

以上例子可以看出，矩陣理論不僅可以用于求解線性方程組，還可以求解線性微分方程，同時判定相應微分方程組的穩定性，為此方程組對應的實際問題提供理論參考。微分方程的求解可應用于多種領域，如SIR傳染病模型、種群模型及電路問題，更進一步可以利用李雅普諾夫矩陣代數方程說明系統的穩定性及未來的發展動態。求解問題主要運用到矩陣的概念、矩陣的乘積、正定矩陣的概念及矩陣的求逆運算。通過實例，可以使學生掌握基礎知識，激發學習興趣，培養創新能力。

對于線性時變控制系統[8]

(2)

其中A(t)∈Rn×n,B(t)∈Rn×m,C(t)∈Rr×n,D(t)∈Rr×m分別是系統(2)的系統矩陣、輸入矩陣、輸出矩陣和反饋矩陣，統稱為系數矩陣，并且是分段連續函數。同樣涉及矩陣的運算，說明矩陣理論影響深刻且應用廣泛。假設A(t)是n-2次可導函數，B(t)是n-1次可導函數，這是對線性代數中矩陣理論的推廣。線性代數中的矩陣運算包括線性運算、乘法運算、求逆運算、數乘及冪運算，并沒有給出求導運算法則，實際上在高等數學課程中，求導運算是最基礎的運算形式，但并沒有推廣到線性代數中。矩陣或向量的求導，只是對每一個分量進行求導即可，所以矩陣求導計算是線性代數矩陣理論的簡單拓展，在上述假設條件下，記

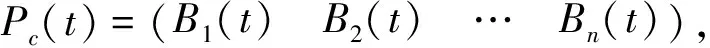
(1)如果存在t>t0，使得R(Pc(t))=n，則系統(2)在t0處可控。

(2)如果存在t>t0，使得R(Po(t))=n，則系統(2)在t0處可觀。

(3)如果系數矩陣均是常值矩陣，有

以上內容是對矩陣理論的簡單應用，主要涉及矩陣的運算及矩陣的秩。這部分內容對于初學者特別是電氣自動化專業學生來說容易接受，為矩陣理論的應用指明了方向。

2 結語

矩陣理論具有鮮明的學科特點，教師應充分利用其優勢，重視學生綜合素質和能力的培養，為學生未來的發展打下堅實基礎。當前，高等教育對線性代數的學習提出了更高要求，不僅需要培養學生對知識理論的學習能力，更要培養學生學以致用的能力，使學生愛學數學、愛用數學，激發思想活力和創造力，培養適應時代發展的復合型人才。