雙層優化估計圖像去噪問題的退火參數

馮象初，衛麗麗

(西安電子科技大學 數學與統計學院，陜西 西安 710126)

由于圖像成像過程中會受到各種因素的影響，得到的初始圖像往往含有不同性質的噪聲，干擾了人們對圖像信息的理解，因此需對圖像進行去噪處理。圖像去噪技術目前已經有很豐碩的成果[1-4]，其中基于變分理論的方法在圖像去噪問題中取得了巨大成功。變分方法的基本原理是設計一個極小化能量泛函，當達到最小化能量狀態時即得到了最優的圖像估計。

在使用變分方法進行圖像去噪時，值得注意的是正則化參數的選取問題。在變分圖像去噪模型中，數據項用于保持原有信息，正則項用于光滑化，合理選取二者之間的正則化參數尤為重要。實際上，學界已經提出了很多種正則化參數選取方法以提升去噪效果，如基于先驗策略選取參數的方法，以及基于后驗選取策略，如Morazov偏差原理[5]，廣義交叉檢驗準則[6]等方法。最近，由于優化學習方法的廣泛使用，KUNISH等[7]將雙層優化問題引入變分模型中，提出了半光滑牛頓算法來求解變分模型中的參數，REYES等在文獻[8-10]中，通過建立雙層優化模型，設計了半光滑的牛頓方法與BFGS迭代算法相結合的求解算法，有效地學習了變分方法去除混合噪聲的兩個標量參數。模擬退火算法[11]則從另一個方面對正則化參數加以改進，其目的是提升計算效率。它選取一組單調增加的參數(稱為退火參數)用于迭代計算，每一步迭代以上一步計算結果作為初值。然而模擬退火選取的退火參數往往是基于先驗知識的，如何利用訓練數據給出最優退火參數的估計是個值得研究的問題。

筆者提出一個新的雙層優化模型用于確定退火參數，在下層問題中增加了新的正則化項以保證解的存在性，同時利用反向傳播(Back-Propagation，BP)算法[12]，提出了優化退火參數的有效算法，最后還給出了一種泛化方式。文中在優化過程中，并沒有強加單調性的要求，而學到的退火參數卻具有單調增加的特性，這表明從數據中學到的算法是符合模擬退火方法假定的。據了解，這是第一次通過訓練數據明確觀測到這種現象。

1 正則化參數的選取

1.1 全變差模型正則化參數

圖像在獲取、傳輸、存儲等過程中時常會受到各種因素的干擾而導致退化現象的產生。圖像退化的數學模型可表示為

f=Ru+n，

(1)

其中，u為原始圖像，f為觀測圖像，R為線性模糊算子(例如卷積算子)，n為噪聲。通常用概率分布描述信號傳輸或處理造成的失真情況，文中噪聲模型均以高斯白噪聲來考慮，即n～N(0，σ2)。

基于變分的圖像恢復模型以圖像退化模型為基礎，將原始圖像的先驗信息引入目標函數作為約束，使得恢復后圖像更接近真實圖像。其中受到廣泛關注的即為Rudin、Osher和Fatemi在1992年提出的全變差模型，也稱ROF模型[13]。他們認為圖像是分片光滑的，可以存在不連續信息。利用此先驗信息和最大后驗估計(Maximum A Posteriori estimation，MAP)給出原始圖像的恢復模型為

(2)

其中，BV為有界變差函數空間，Ω是有界開區域，具有Lipschitz邊界，λ為正則化參數，?為梯度算子。式中第1項稱為保真項，用來保證恢復圖像與觀測圖像之間距離足夠小；第2項稱為正則項，用來懲罰圖像的不連續點，在去除噪聲的同時能夠很好地保持邊緣結構。

當模糊算子R=I時，式(2)即為經典的去噪模型：

(3)

式(3)的數值求解方法如下：根據變分原理，其相應的Euler-Lagrange方程為

(4)

結合梯度下降法將式(4)轉化為偏微分方程：

(5)

使用合適差分形式求解式(5)式，得

(6)

當取0<λ?1時，恢復圖像u≈f。當取λ?1時，恢復圖像u≈c(常數)，如圖1所示。從結果可看出參數λ起著平衡兩項的關鍵性作用，參數λ越小，恢復圖像越接近噪聲圖像；參數λ越大，恢復圖像就越光滑。因此可看出正則化參數的選取十分重要。

(a) 噪聲圖(σ2=202)

1.2 雙層優化估計最優正則參數

(7)

其中，u*表示原始圖像，ε是附加正則項對應系數。文獻[10]給出了解的存在性定理。

定理1[10]對于u，f∈BV(Ω)∩L2(Ω)，ε>0，問題(7)存在最優解λ，且滿足λ>0。

1.3 模擬退火方法

模擬退火方法則從另一個角度考慮正則化參數的作用。在式(6)的迭代中，初始值u0是從f出發，迭代直到收斂。為了提高計算效率，借用模擬退火方法的思想，取λk單調遞增，使得λk→λ，每次迭代以上一次迭代的結果作為初始值，從而有

(8)

2 最優退火參數的估計

2.1 最優退火參數估計模型的建立

受到雙層優化估計最優正則化參數方法的啟發，文中希望可利用訓練數據估計最優退火參數，故此建立雙層優化模型如下：

(9-1)

(9-2)

(9-3)

2.2 模型的求解

對于式(7)的求解，文獻[9]中利用對偶形式和半光滑牛頓法求解上述雙層優化問題。由于式(9)下層問題每次迭代過程參數都是不同的，因此為了求解最優的退火參數，利用反向傳播算法，提出了一種新的求解方法。

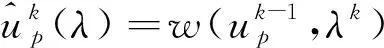
圖2 迭代展開網絡

對于上述N層網絡優化問題，可根據BP方法進行求解。BP方法是由信號的正向傳播與誤差的反向傳播兩個過程組成，經過信號正向傳播與誤差反向傳播，不斷地調整每層網絡中的參數，直至達到最優。具體的推導過程如下所示：

對于式(9)，存在一個拉格朗日乘子B(k)，使得

(10)

根據拉格朗日乘子法，可知式(10)解需要滿足下列條件：

(11-1)

(11-2)

(11-3)

對于式(11-1)求解：

對于式(11-2)，通過計算求解可得

由于該問題為一個固定點問題，式(11)即為駐點條件。為了尋找極小值在此運用了最速下降的方法，即

(12)

綜上分析，雙層優化估計退火參數求解算法，具體步驟如下：

步驟1 輸入噪聲圖f1，…fP，初始退火參數λ1，…λN，時間步長Δt，參數η，迭代次數iter。

沙三下砂礫巖體儲集物性與含油性密切相關，因此含油性預測即為儲集物性預測。而儲集物性與沉積特征、地層壓力和構造應力特征密切相關。

步驟3 循環迭代：

由式(11-2)計算Bp(k)；

由(12)式更新λk；

步驟4 判斷：如果迭代次數大于iter，則停止迭代；否則，繼續迭代；

步驟5 輸出：恢復圖u1，…up，最優退火參數λ。

3 數值仿真

3.1 參數確定以及模型去噪效果

文中算法均在HP-Z230(4核3.30 GHz CPU和16 G RAM)平臺上實現，Matlab R2018b編程環境在Windows 7操作系統中運行。選取圖像恢復數據集(USC SIPI-Misc)以及一些常用的圖像(如lena、house、cameraman、peppers等)進行實驗。

由于文中模型是基于統計學的最大后驗估計提出的，在保證泛化能力的同時，模型中每層僅有一個參數需要修正，少量樣本的訓練即可得到收斂的結果，增加訓練樣本，退火參數值變化微小。實際上，筆者利用了20對圖像進行訓練，圖3給出了噪聲標準差為20時，其中8對訓練樣本圖像。對于所提算法中其它超參數的選取，根據實驗研究，深度N=16時已經得到了很好的效果，隨著N的增加，PSNR值的變化僅在0.005左右，差別微小，故在此選取超參數值N=16，Δt=0.002，η=0.04，ε=0.01，iter=400。退火參數初值λk選為0.5，對其進行一定范圍的波動，與最終確定的參數得到的實驗效果相差很小，說明算法對初值具有一定的穩定性。

(a) 干凈圖 (b) σ2=202帶噪圖

噪聲標準差為20時，實驗所得最優退火參數[λ1，…，λ16]=[0.887 6，0.990 5，1.049 8，1.149 0，1.282 9，1.413 6，1.573 6，1.742 4，1.942 0，2.194 2，2.461 4，2.801 6，3.239 1，3.698 0，4.592 3，5.577 9]利用所得最優退火參數，從常用恢復圖像數據集中隨機選取更多的與訓練集不同的圖像進行測試，結果表明雙層優化估計退火參數算法有著很好的去噪效果，表1(左3列)隨機給出了其中6幅測試圖像的結果。同樣地，算法也可以直接應用于彩色圖像去噪問題，相同的實驗過程，表1(右3列)隨機給出了6幅彩色圖像測試結果。

對上述20幅圖像加上其他方差的噪聲構成訓練樣本對，利用式(9)估計對應的最優退火參數。表2給出了噪聲標準差為1，5，8，10，15，25訓練樣本對實驗所得相應最優退火參數值，表中每一列為對應于同一個噪聲方差的16個最優退火參數值，每一行為給定的退火參數在7個不同噪聲條件下的最優值。隨后，利用不同噪聲方差最優退火參數分別對同樣噪聲下的測試集進行測試，結果表明雙層優化估計退火參數算法均有著很好的去噪效果，表3給出了其中部分實驗結果。

表1 標準差為20的測試圖像去噪的結果(PSNR)) dB

表2 不同噪聲方差下最優退火參數的估計值

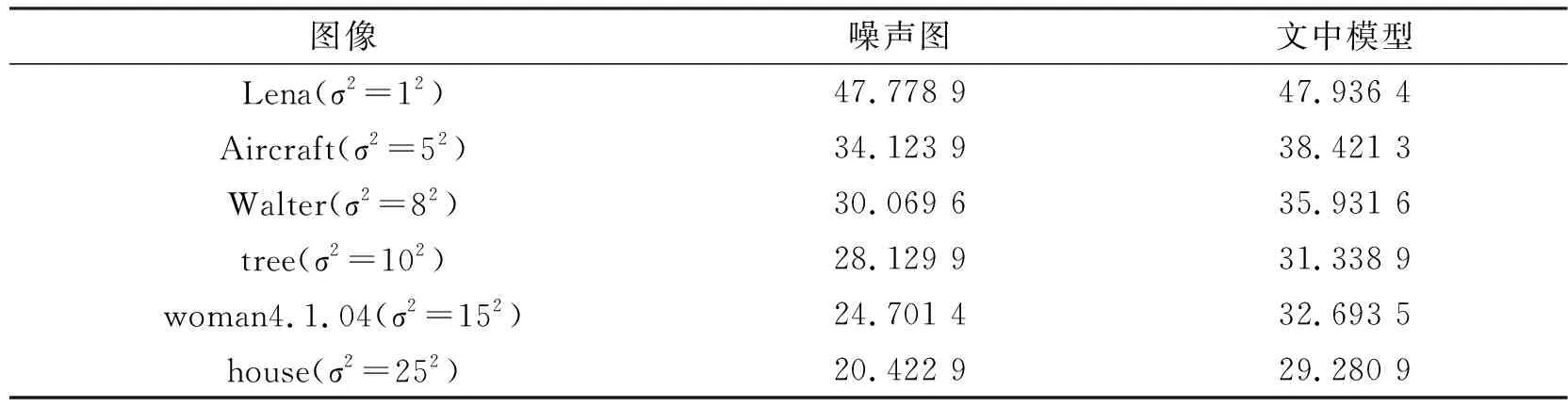
表3 不同方差噪聲下測試圖像的去噪結果(PSNR) dB

3.2 和其他模型去噪效果對比

為了進一步評價文中基于雙層優化學習的退火參數方法的有效性，選用常用的基于先驗的參數選取方法模擬退火方法和基于后驗的選取方法廣義交叉驗證準則方法，與文中算法進行了大量的對比實驗，新方法均取得了較好的結果。實際上，將雙層優化應用于模擬退火算法中后，提升了參數的估計精度，去噪結果也平均提升了0.1 dB。計算效率方面，當參數確定后，任一測試圖像僅需有限次迭代即可完成，計算復雜度為O(N)，表4給出了3個比較結果的例子。

表4 利用不同的參數選取模型去噪的結果對比(PSNR) dB

3.3 基于學習的退火參數分析

對雙層優化估計所得退火參數進行具體分析，從表2每一列可以看出，固定噪聲方差，隨著k的增加參數均呈單調遞增趨勢，和模擬退火算法增長趨勢是一致的，說明隨著k的增加，正則化項也在相應地加強。模擬退火方法是基于先驗知識的算法，λk的單調遞增方式也是先驗設定的。利用數據學習的方法，可以從數據中自適應地學習到一組最優的參數增長方式，如圖4所示。注意到在優化過程中，并沒有強加單調性的要求，因而從數據學習的角度表明了迭代過程中正則化參數單調增加的合理性。據檢索所知，這是第一次通過訓練數據明確觀測到這種現象。

(a) σ2=102

從表2每一行可以看出，隨著噪聲方差的增加，退火參數也是增加的，表明正則項的作用在加強；而在另一個方向上，當噪聲方差減小趨于0時，退火參數收斂到0，這和正則化參數的收斂性要求是一致的。圖5給出了3個參數的圖示。

3.4 算法自適應性分析

通過對自然圖像的訓練樣本學習，得到了相應的最優退火參數及單調遞增的變化趨勢。為了研究最優參數對訓練數據的自適應性，我們選取一類紋理圖像數據作為訓練樣本，分別對噪聲標準差為10，15，20的情形進行類似的實驗。學習得到相應的最優退火參數如圖6所示。結果表明，迭代過程中正則化參數數值和單調增加模式是根據不同的訓練數據自適應調整的。

(a) 參數λ2

(a) σ2=102

4 插值泛化

式(9)是針對給定的噪聲方差，估計對應的最優退火參數。利用這個模型，給出了7種不同方差噪聲對應的最優退火參數(表2，圖5)。為了處理其它方差噪聲圖像的恢復問題，可用文中算法得到的最優退火參數去估計其他方差的最優退火參數。從4.3節分析可看出對每層的退火參數，隨著噪聲方差的增加，退火參數也在不斷地連續增加，表明退火參數也是依賴于噪聲方差的連續的單調遞增函數(圖5)。因此可根據已知所得數據，通過插值的方法估計出其他噪聲方差下的最優退火參數。

通過上述分析，利用表2數據進行實驗，選用3次拉格朗日插值方法[18]估計其他噪聲方差圖像的退火參數。3次插值樣本點取估計方差左右最近的4個點。利用插值估計的退火參數，分別對其相對應噪聲測試集圖像進行實驗，結果表明插值估計所得退火參數同樣有著較好的去噪效果，這也說明了文中算法有著較好的泛化能力。表5給出了插值泛化方法對4個不同噪聲方差測試圖像Lena去噪結果。

表5 插值泛化測試圖像的去噪效果(PSNR) dB

5 結束語

結合雙層優化方法，筆者提出了退火參數估計的學習模型，設計了退火參數估計的有效算法。值得指出的是，優化問題中未加任何單調性約束條件，學習得到的退火參數卻表現出單調遞增趨勢，因而從數據學習的角度表明了迭代過程中正則化參數單調增加的合理性。相較現有常用的基于經驗的參數選取方法，新方法從訓練樣本中自適應學習到數值最優的退火參數和變化模式，從而使退火模型既保證了計算效率，也擁有了較好的去噪效果。最后，文中提出了一種簡單的插值泛化方法，表明了所提算法有著很好的泛化能力，使提出的模型可以適應不同強度的噪聲去除問題。仿真實驗表明了方法的可行性和有效性。

文中主要討論了加性高斯噪聲下的圖像去噪問題，研究了利用雙層優化選取最優退火參數的模型和數值解法。在今后研究中將進一步地把所提方法推廣到混合噪聲去噪等問題中。