基于MPC的無人駕駛汽車軌跡控制研究

蔡志鑫，古永鵬，董 浩，程琳源

基于MPC的無人駕駛汽車軌跡控制研究

蔡志鑫，古永鵬，董 浩，程琳源

（長安大學 汽車學院，陜西 西安 710064）

為更好地實現對無人駕駛汽車行駛路徑的跟蹤修正，基于模型預測算法控制車輛的車速和橫擺角。通過建立車輛運動學模型、制定目標函數、確定約束條件，設計出了軌跡跟蹤控制器。并通過Matlab/Simulink、CarSim軟件搭建模型預測控制算法。結果顯示，在預定工況下，車輛參考路徑和實際行駛誤差較小，并有較好的橫向穩定性。結果表明該算法能在一定程度能保證無人駕駛汽車的安全性，為智能車輛控制提供了基礎。

無人駕駛汽車；模型預測控制；軌跡跟蹤；運動學模型

引言

汽車發展至今，已經從交通工具轉變為了多種技術的載體。隨著工業革新和技術進步，汽車產業與移動互聯、大數據、云計算、人工智能、電子電器、新材料等領域加速融合，使得新能源汽車和智能駕駛已經成為汽車行業發展的新風潮。目前國內除傳統汽車制造企業外，百度、小米、阿里、華為等互聯網公司也紛紛進軍智能車的領域，進一步加速了智能汽車的發展。而無人駕駛汽車作為智能車的一種，其能夠減少事故發生率、實現文明行車、緩解交通擁堵等問題[1]。對于未來的智能交通系統，無人車的發展成為一種必然趨勢。

跟蹤問題是無人駕駛車輛重要的環節。它是指根據某種控制理論，為系統設計一個控制輸入作用，使無人駕駛車輛能夠到達并最終以期望的速度跟蹤期望軌跡[2]。由于汽車是一個典型的非完整約束系統，這使得對車輛的控制更加復雜。而模型預測控制算法具有多模型約束處理優勢，能很好地與規劃控制、環境感知數據處理結合，是體現無人駕駛汽車運動學和動力學約束的理想控制方法。

1 模型預測控制原理

模型預測控制理論在無人駕駛車輛路徑生成和跟蹤控制中應用廣泛。該理論可在控制過程中增加多種模式的約束，使其滿足車輛動力學特性。模型預測控制是通過預測模型、滾動優化、反饋校正三個步驟實現的[3]。

1.1 預測模型

預測模型是實現模型預測控制的基礎。其根據被控對象的歷史信息和當前系統輸入信息，來預測系統未來的輸出。

1.2 滾動優化

模型預測算法相較于傳統最優控制算法，它可將被控系統的某項性能評價指標作為最優控制量。通過反復在線優化，滾動地完成優化問題。

1.3 反饋校正

在線求解開環優化問題是模型預測控制算法的獨特優勢。但由于在實際控制過程中可能會出現非線性、模型失配、環境擾動等不可抗條件，那么可在新的采樣時刻，檢測被控對象的實際輸出，在線對預測信息進行修正，從而進行新的優化。

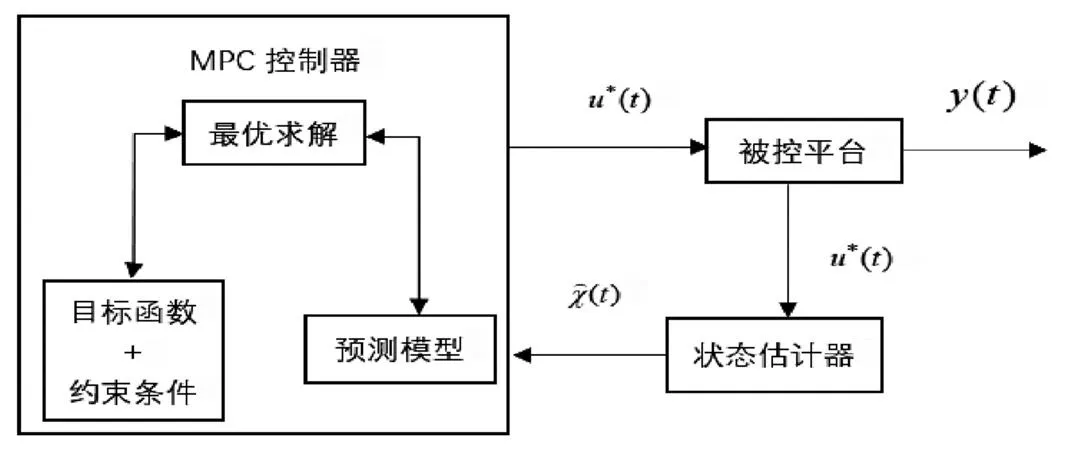
圖1 模型預測原理

模型預測控制原理如圖1所示[4]，分別由MPC控制器、被控系統和狀態估計器三個模塊組成。首先MPC控制器通過預測模型、目標函數+約束條件進行最優化求解，得到當前最優控制序列。被控對象執行當前控制量時，將當前狀態量觀測值輸入狀態估計器。狀態估計器對無法感知的狀態量進行估算，并將其估算量輸入MPC控制器，然后進行下一控制序列的最優求解[5]。

2 車輛運動學建模

車輛運動學模型是依據幾何學研究車輛運行規律，包括車輛位置、速度等變化。當車輛在良好路面行駛時，通常不考慮車輛操縱穩定性等動力學問題，這時基于運動學模型設計的路徑跟蹤控制器具備可靠的控制性能。

2.1 車輛運動學模型

車輛運動學模型如下圖2所示：

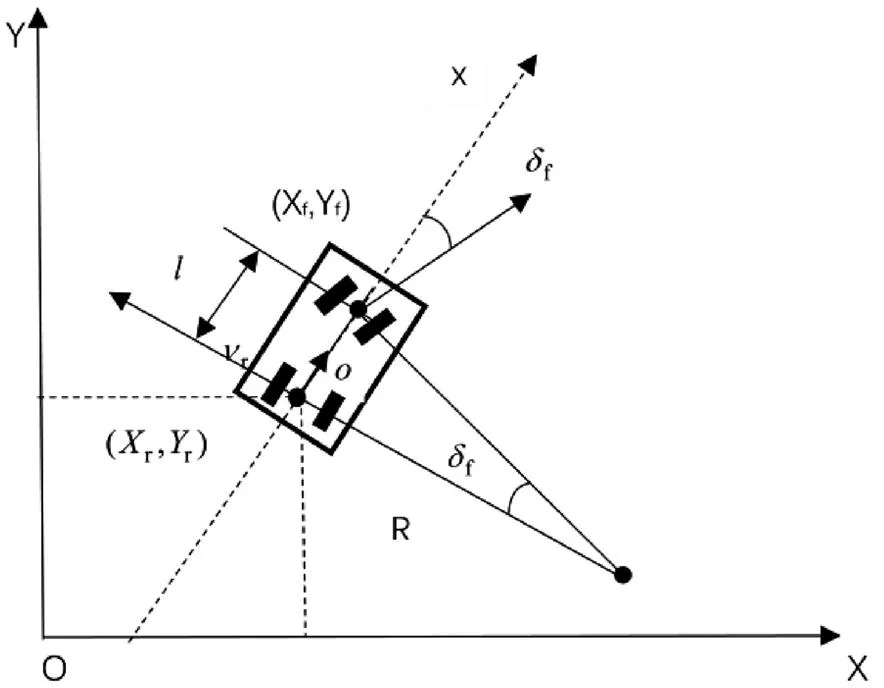
圖2 車輛運動學模型

在地面坐標系中，建立車輛運動學方程：

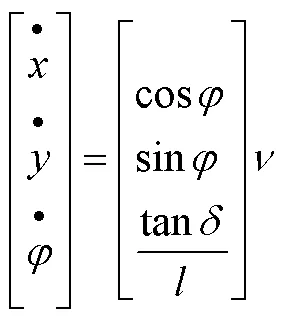
上式中，(,)為車輛后軸中心坐標，為車體航向角，為前輪偏角，為車輛后軸速度，為軸距。

由式（1）可知，系統可看作一個輸入=(,)和狀態量為(,,)的控制系統，用代表參考量，其一般形式為：

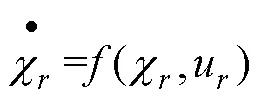
其中χ=[x y φ], u=[v δ]，對式（2）在參考軌跡點采取泰勒級數展開并忽略高階項，得到：

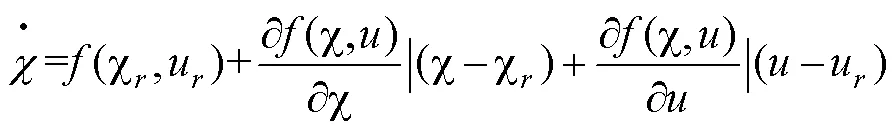
為得到無人駕駛車輛誤差模型，（3）與（2）相減，得：

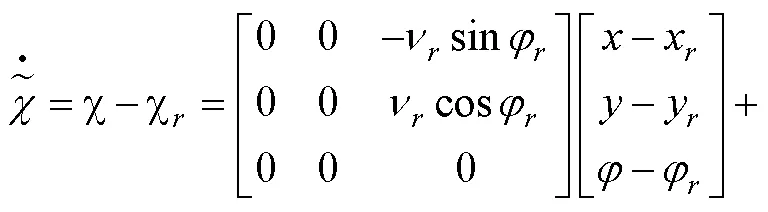
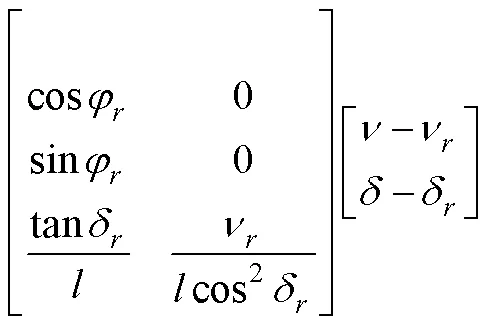
對（4）進行離散化處理：

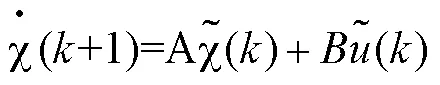
其中：

2.2 設計目標函數

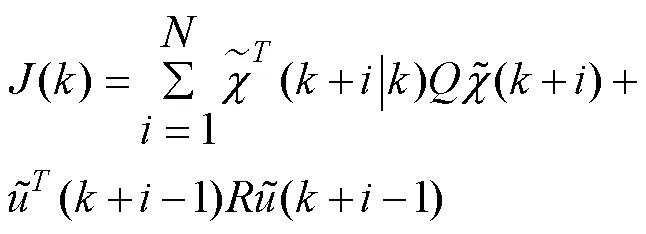
為保證控制量的連續性，在式（6）添加軟約束，則目標函數轉化為：

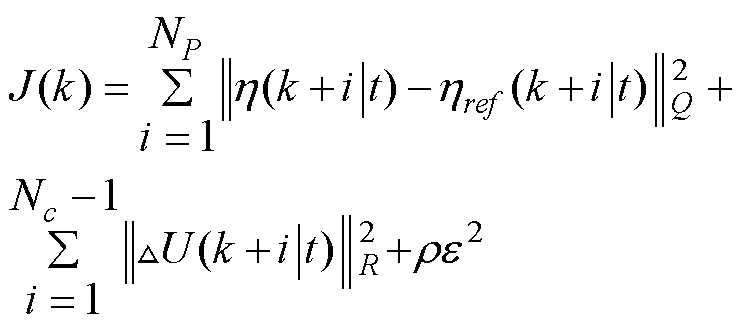
其中，N為預測時域，N為控制時域，為權重系數，為松弛因子。

2.3 約束條件設計

控制過程中控制量表達形式為：

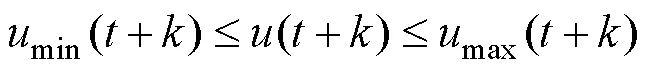
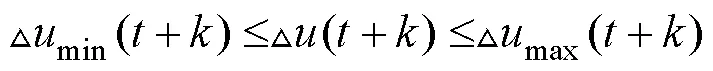
=0，1，…N－1

因目標函數的限制，約束條件只能以控制增量或者控制增量與轉化矩陣相乘，因為存在如下關系：

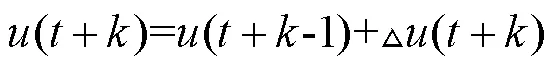
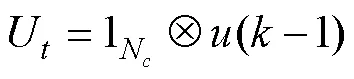
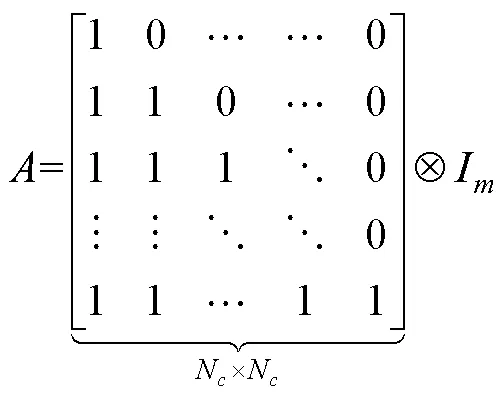
將式（8）轉化為如下形式：

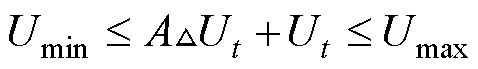
將目標函數轉化為標準二次型并結合約束條件，解決如下優化問題：

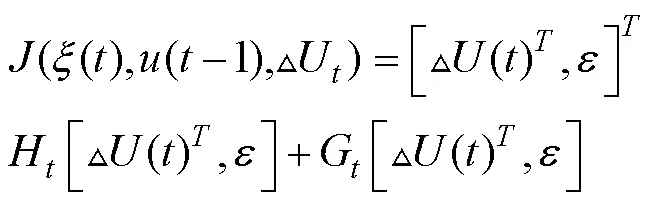
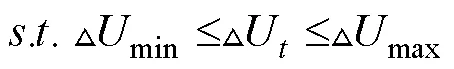
在完成每一控制周期內，對式（13）的求解后，得到控制時域內的一系列控制輸入增量：

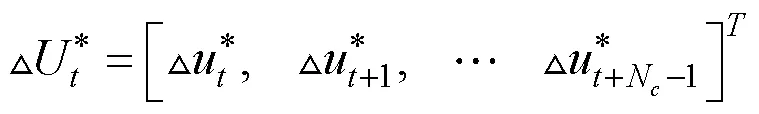
將該控制序列中第一個元素作為實際的控制輸入增量作用于系統，即：

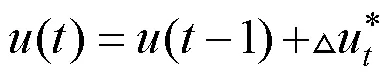
進入下一控制周期后，重復操作，可實現對車輛的軌跡跟蹤控制功能。

3 Matlab和CarSim聯合仿真

利用Matlab/Simulink和CarSim軟件建立聯合仿真平臺來實現模型預測控制的軌跡跟蹤控制。通過CarSim軟件搭建車輛模型并設置仿真工況。通過Simulink的S-Function函數設計軌跡跟蹤控制器。通過設置輸出端和輸入端，實現聯合仿真[6]。建立的模型如圖3所示。

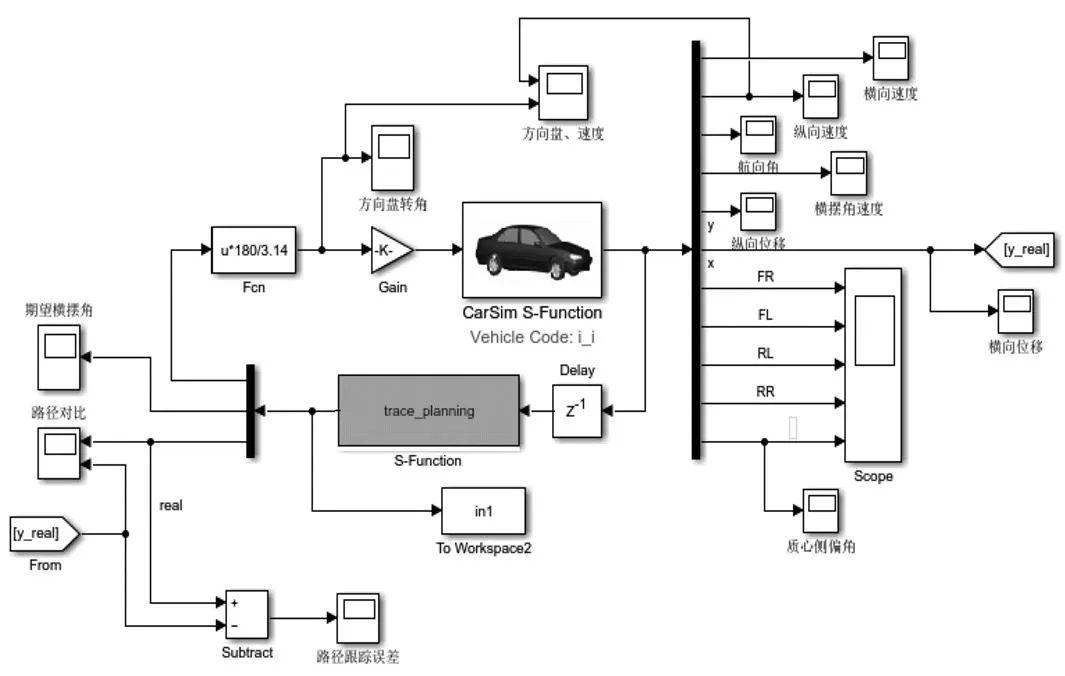
圖3 CarSim與Simulink聯合仿真模型

仿真結果如圖4—圖7所示。

由仿真結果圖（4）可以看出，車輛實際行駛路徑和期望路徑基本吻合，車輛經歷了轉向—回正—轉向—回正的過程，且路徑跟蹤誤差最大不超過±0.04，行駛路徑達符合預期要求。由圖（6）可知，車輛在轉向過程中側向加速度為－0.2 m/s2≤a≤0.2 m/s2，具有良好的穩定性和安全性。圖7表明在車輛轉向時，轉向盤能及時擺動，使得車輛能跟上預定軌跡，且擺動誤差也較小。綜上所述，本文建立的控制器能夠快速較好地進行軌跡跟蹤，并具有精度高、響應快速、跟蹤穩定、安全可靠的特點，基本滿足設計要求。

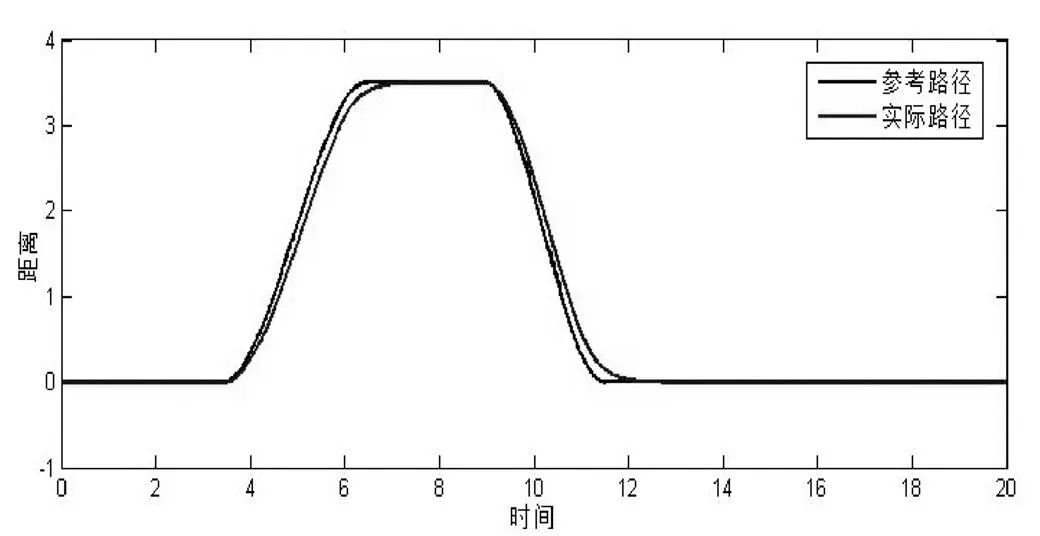
圖4 參考路徑與實際路徑對比

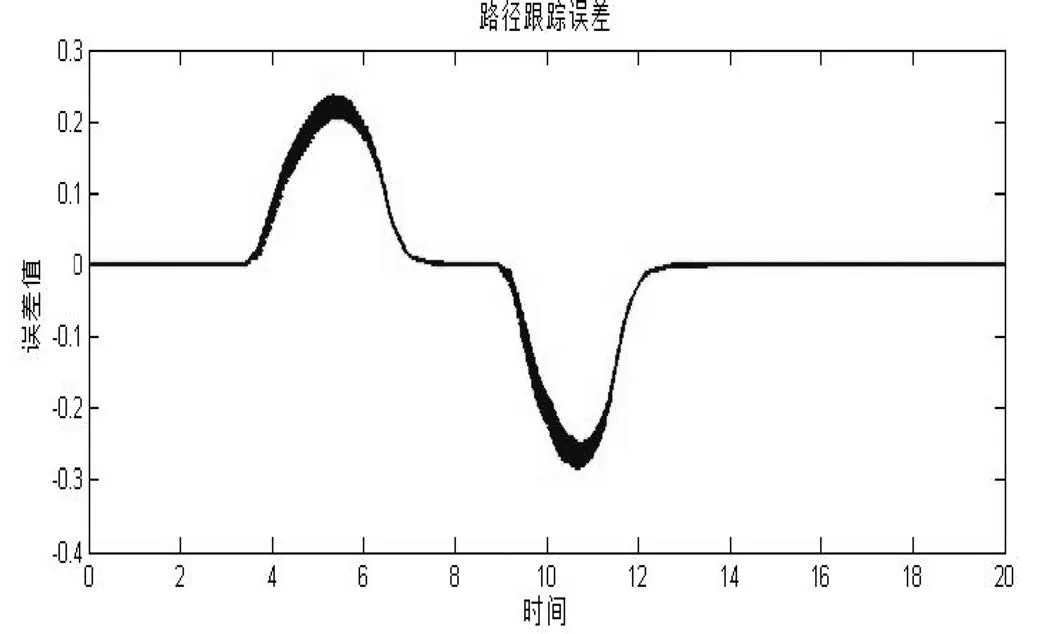
圖5 路徑跟蹤誤差

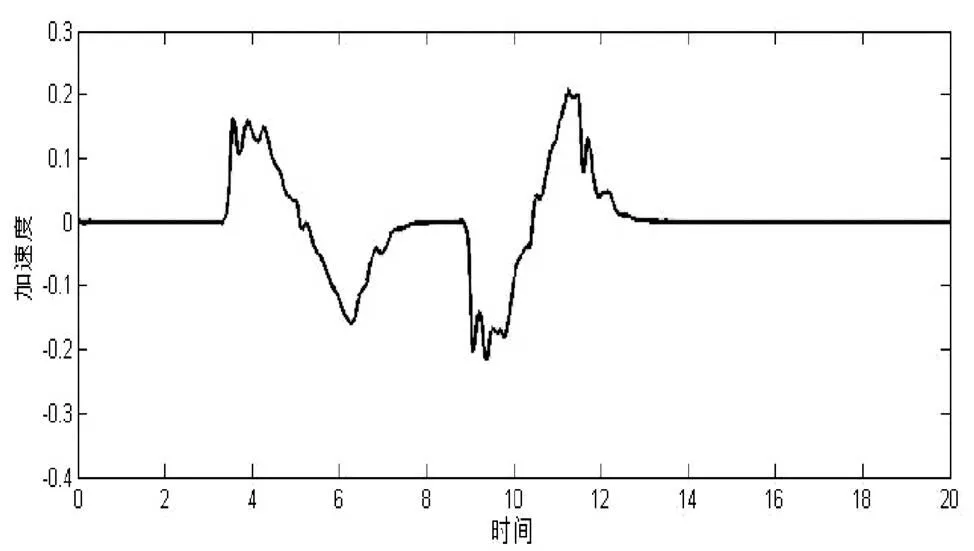
圖6 車輛側向加速度變化

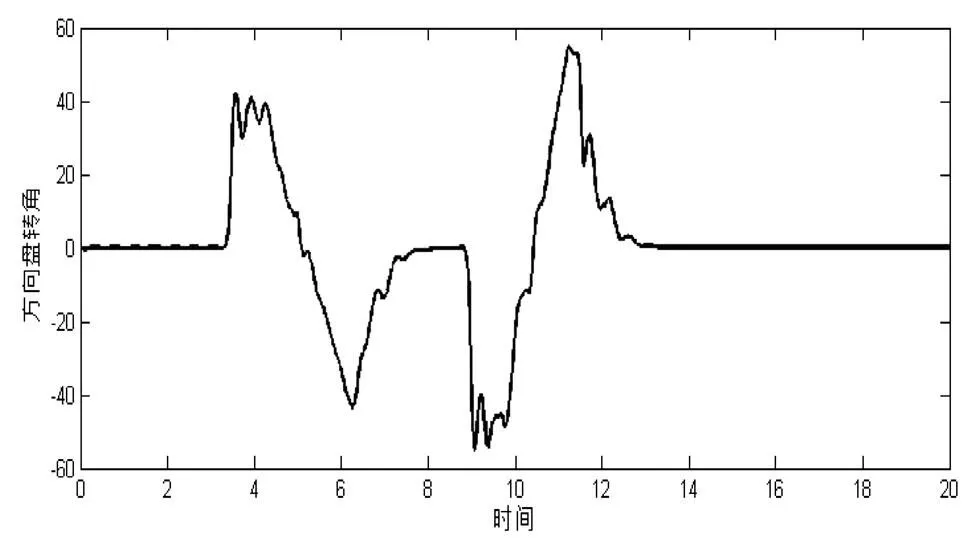
圖7 方向盤轉角變化

4 總結

本文以車輛運動學模型為基礎，通過模型預測算法，設計了軌跡跟蹤控制器。利用Matlab/Simulink和CarSim軟件搭建聯合仿真平臺驗證了控制算法的有效性。通過車輛在預定工況下行駛，得到了軌跡跟蹤控制器的控制效果。對仿真結果分析后發現，本文設計的無人車軌跡跟蹤控制能基本完成目標任務，具有一定的穩定性、安全性，能有效地控制車輛的行駛路徑。為無人駕駛汽車的避障、換道等行為提供了一種可靠的方法，具有一定的實用性和可行性。

[1] 孟建平.汽車主動換道軌跡規劃與跟蹤控制研究[D].合肥:合肥工業大學,2020.

[2] 龔建偉,姜巖,徐威.無人駕駛車輛模型預測控制[M].北京:北京理工大學出版社, 2014.

[3] 潘魯彬.無人駕駛汽車的路徑規劃與跟隨控制算法研究[D].長沙:湖南大學,2016.

[4] 黃豐雨.基于模型預測控制的無人車動態路徑規劃與跟蹤優化研究[D].武漢:武漢理工大學,2019.

[5] 劉陽.輪轂驅動電動汽車自主換道策略研究[D].長春:吉林大學,2020.

[6] 單曉萌,王靖岳,王浩天.基于MPC的無人車運動軌跡跟蹤控制研究[J].機械工程師,2020(09):45-47.

Research on Tracking of Unmanned Vehicle Based on MPC

CAI Zhixin, GU Yongpeng, DONG Hao, CHENG Linyuan

( School of Automobile, Chang'an University, Shaanxi Xi'an 710064 )

In order to better realize the tracking and correction of the driving path of the driverless car, the speed and yaw angle of the vehicle are controlled based on the model prediction algorithm. By establishing the vehicle kinematics model, formulating the objective function, and determining the constraint condi- tions, the trajectory tracking controller is designed. And build model predictive control algorithm through Matlab/Simulink and CarSim software. The results show that under predetermined conditions, the vehicle reference path and the actual driving error are small, and there is good lateral stability.The results show that the algorithm can guarantee the safety of driverless cars to a certain extent, and provides a basis for intelligent vehicle control.

Self-driving vehicles; Model predictive control; Tracking; Kinematic modelCLC NO.: U495

B

1671-7988(2022)01-24-04

U495

B

1671-7988(2022)01-24-04

蔡志鑫（1995—），男，碩士研究生，長安大學汽車學院，研究方向為汽車電子技術。

10.16638/j.cnki.1671-7988.2022.001.006