基于Hash函數抗軟磨硬泡攻擊算法的設計與實現

馬文亭

(哈爾濱華德學院，哈爾濱 150025)

信息的安全性已逐漸引起人們的重視。在密碼學分析中存在一種Rubber-hose攻擊[1]，在這種攻擊中，如果受害者不給出密鑰，分析者將會折磨、威脅、恐嚇、勒索受害者。這些攻擊毫無技術性，但卻是非常有效的攻擊方法，也是破譯算法最便捷的途徑。

分析了現有的誤導低冗余加密方法，在保證算法功能的前提下提出了新的加密方案，提高了算法的安全性，降低了冗余度。通過實驗測試結果顯示，該改進方案可以使具有誤導功能的低冗余加密算法的安全性得到了很大的提升。

1 具有誤導性的加密算法

1.1 算法的意義

由于其他密碼分析方法的條件難于獲得，現實中軟磨硬泡攻擊經常是破解算法的最好途徑，所以其價值具有現實意義。它可以對抗無限計算能力或在很強的計算能力下的各種密碼分析，甚至是唯密文分析。在密鑰可能被盜取的情況下，可以用偽密鑰作為誘餌誤導對方，它可以主動誤導對方，錯誤密鑰可以得到有意義的明文再誤導對方，并用偽密鑰得到各種相近、相反的明文，相較于原始明文，具有一定的抵消作用，令密碼分析者無所適從[1]。

1.2 算法的原理

該算法采用內外兩層加密。內層加密是該算法的核心，類似于選擇題，外層加密方法則采用對稱加密。將同一類的關鍵詞放在一組中，每一個關鍵詞在對應的組號中都有唯一的編號。在設計關鍵詞數據庫時，必須保證關鍵詞組不相同，將明文與數據庫進行字符匹配，若有關鍵詞則用擴充項替換關鍵詞。為了方便解密操作，選擇3個保留編碼或在文本中不出現的符號分別作為擴充項的起始標記S、分隔標記D和結束標記F。假設明文中關鍵詞在數據庫中對應的一組的編號是H，在這一組中的獨立編號是a，這一組中關鍵詞的數目為n，Ks是內層加密的子密鑰，Ext為擴充項：

T=Ks+amod(n)

Ext=S+H+D+T+F

通過以上操作，將明文中的關鍵詞替換為擴充項生成過渡密文，再利用AES算法對過渡密文進行加密，生成密文。

1.3 算法的不足

1.3.1 算法的安全性低

理論上該算法是安全可行的，但是理論上可行的算法不代表在實際操作中可行，密碼學研究者發現了AES算法的弱點，令破解密鑰的速度更快。攻擊者可以通過某種方式破解外層加密，獲得過渡密文。假如攻擊者得到過渡密文中的擴充項，因為擴充項中的組號是H和代號T都是以原有的形態保留，故而，攻擊者就得到了關鍵詞的組號和編號。

1.3.2 密鑰的安全性低

密鑰是一個算法的重要保障，密鑰的安全性等同于算法的安全性。誤導的低冗余的算法會根據密鑰的改變來得到不同的偽明文。一旦密鑰被密碼分析者攻擊，得到真實的密鑰就可以得到真實的明文，所以密鑰的安全性是至關重要的。但是該原有的誤導的加密算法并沒有對密鑰進行任何保護。

2 基于Hash函數抗軟磨硬泡攻擊算法

2.1 提高算法的安全性

在原有的算法中，因為擴充項的原因，使得算法的安全性低，所以提高擴充項的安全性也是提高算法的安全性。擴充項=起始標記S+組號H+分隔標記D+代號T+結束標記F，其中，H和T是以數字的形式存儲在擴充項中[1]。基于Hash函數抗軟磨硬泡攻擊算法采用了Base64編碼對H和T進行編碼，Base64編碼[2]具有不可讀行，因此，編碼的數據無法通過觀察得到。原有的算法不僅要具有誤導性，還需要具有低冗余，所以Base64編碼比其他的加密方法更為適合。一般情況下，H和T都不會過大，而字符串進行Base64編碼后，至少比原來長1/3。其中，組號H和代號T都是數值，所以利用Base64編碼不會大幅度地增加冗余。

算法步驟如下：假設Key是算法的密鑰，對H進行Base64編碼，再對T進行Base64編碼，但是這里的T已經不是原有算法的T了，雖然也是關鍵詞的代號，但是這個T是對子密鑰KS進行函數運算，再將代號T和組號H進行Base64編碼，和S、D和F共同組成擴充項EXT：

T=Hash(K.substring(16))+a mod n

Ks=K.substring(16)

EXT=S+encodeBase64(H)+

+encodeBase64(T)+F

Hash()函數是根據關鍵詞在組內的編號，對Ks進行哈希運算，例如：關鍵詞在組內變化是4，則對Ks進行4次哈希運算，具體算法如下：

Public int Hash (String st) throws Exception {

String ha = st;

for (int j = 0; j <= n; j++)

{

ha =String.valueOf(ha.hashCode());

}

return Integer.parseInt(ha);

}

對Ks進行以上的函數運算，使得Ks的安全性更高，代號T在擴充項是以亂碼的形式出現，令關鍵詞的子密鑰得到保護。對于原來擴充項中的H和T，都進行了Base64編碼，形成了新的擴充項EXT。

2.2 提高密鑰的安全性

在本算法中，由于有內外雙層密鑰且密鑰的位數要大于256 bit，日常生活中將密鑰完全牢記的可能性低，所以算法的密鑰就要進行存儲。涉及存儲就可能危害到密鑰的安全性，一旦密鑰被密碼分析者發現，就存在密鑰被修改或被竊取的情況。保證密鑰的安全性也是保證算法的安全性，對密鑰的安全性保護具體如下：

要用一個具有特殊意義或容易記住的字符串作為密鑰保護的口令。利用MD5算法對口令進行運算得到256bit的哈希值。利用哈希值作為新的密鑰，采用AES加密算法對算法密鑰進行加密，對加密的密文進行存儲。解密時，要輸入密鑰保護的口令進行解密操作。

3 實驗驗證

實驗數據采用含有多個關鍵詞的文本文檔，分別對原有的誤導加密算法和改進的誤導加密算法的安全性進行實驗驗證。關鍵詞數據庫可以根據用戶的需求進行自定義，建立需要保護的關鍵詞表格。測試數據是從網絡上隨機截取的字符串，如下：星期五我放假，我們看電影吧，下午三點鐘我在教學樓等你。

根據測試數據的內容，可以建立3個關鍵詞數據表用于實驗驗證(表格可以根據用戶想要保護的內容建立)。分別是時間、地點和事件的關鍵詞數據表格，如表1所示。

假如想保護的數據是準確的時間“三點鐘”，就可以建立新的關鍵詞數據表格。例如：一、二、三分別對應數值0、1、2。

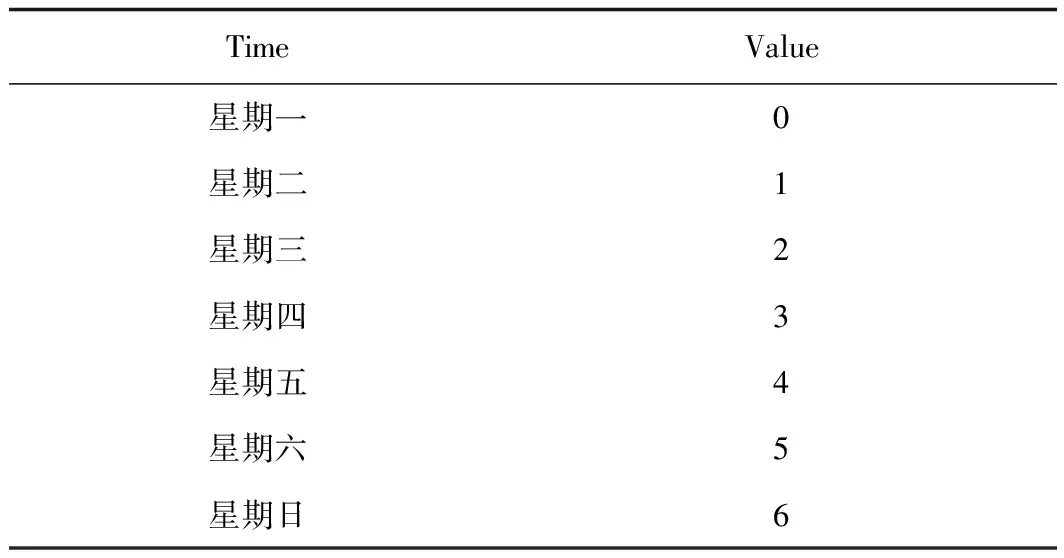
表1 時間關鍵詞表格Tab.1 Time keywords

3.1 誤導性加密算法測試

根據原有的具有誤導功能的加密算法編寫的代碼，對測試數據經行誤導的加解密測試，密鑰是929117xingfanafdga123，加密成功。過渡密文如圖1所示，其中關鍵詞已經被擴充項替換，非關鍵詞不進行任何操作，直接輸出形成過渡密文。

圖1 原算法的過渡密文Fig.1 Transition ciphertext of original algorithm

保持密鑰前256bit不變，更改其余的字符串，例如：解密密鑰為929117xingfanafdga12q，解密仍然可以成功，且此時的關鍵詞已經被同組的其他關鍵詞替換且語義通順。

圖2 偽明文Fig.2 False proclaimed writing

3.2 基于Hash函數抗軟磨硬泡攻擊算法的測試

為了確保驗證的準確性，關鍵詞數據表格、測試數據和加密密鑰都保持不變。使用改進的算法對測試數據進行誤導加解密，得到的過渡密文如圖3所示：

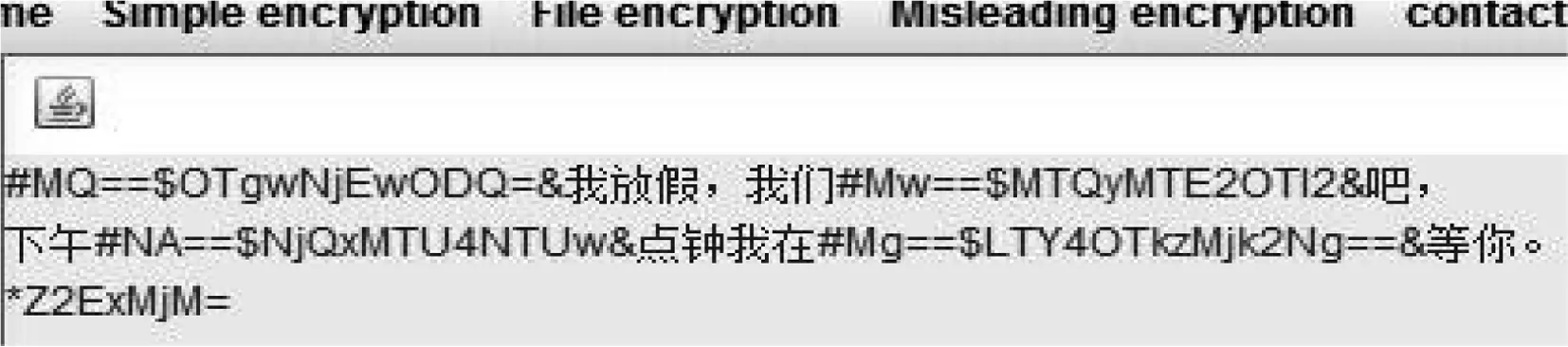
圖3 改進算法的過渡密文Fig.3 Transition ciphertext of improved algorithm

解密時修改密鑰為929117xingfanafdga12q。解密成功得到的偽明文如圖4所示：

圖4 改進算法的偽明文Fig.4 False proclaimed writing of improved algorithm

進行加解密操作之后，需要對密鑰進行保護，對密鑰的密文進行存儲。需要密鑰進行誤導解密時，輸入事先定義好的口令就可以得到密鑰。

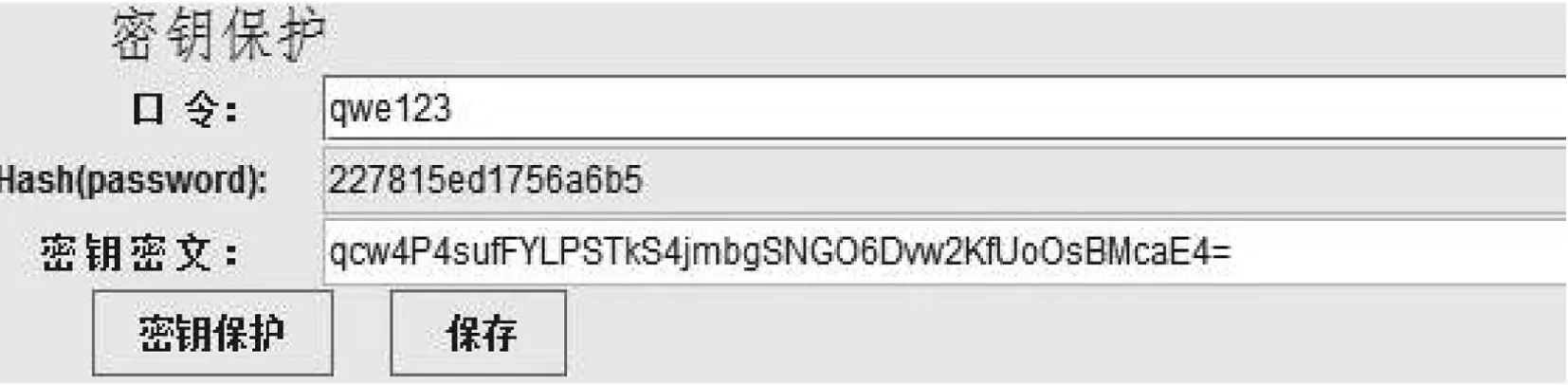
圖5 誤導密鑰的保護Fig.5 Misleading key protection

圖6 誤導密鑰的獲取Fig.6 Misleading key acquisition

在原算法中，測試數據中關鍵詞“星期五”被替換為“#1$98061084&”。根據加密的原理可知，“#”為起始標記，“$”為分隔標記，“&”為結束標記。易得關鍵詞組號：H=1(第一個表單)，關鍵詞代號：T=98061084。根據以下公式:

a=(T-Ks)mod n

Ks=Integer.parseInt(key.Substring(16).hashCode())

Ks=98061080

a=(98061084-98061080)mod 7=4

由公式推導可知，關鍵詞“星期五”是第一組關鍵詞，編號是4。

在改進后的算法中，在過渡密文中，關鍵詞“星期五”被替換為“#MQ==$OTgwNjEwODQ=&”。與原有算法的擴充項相比，該擴充項中沒有出現確切的數字，且每個擴充項都有很大的差別。改進后的算法無法在得到擴充項的前提下得到關鍵詞所在的組號和編號。

3.3 結果分析

根據以上對誤導加密算法和基于Hash函數抗軟磨硬泡攻擊算法的分別測試，可以得到2個不同的過渡密文。對于原有的具有誤導功能的加密算法，關鍵詞被字符和數字組成的字符串代替，如果密碼分析者得到了加密的算法原理，就可以根據數學推導得到關鍵詞的組號和編號。綜上所述，基于Hash函數抗軟磨硬泡攻擊算法很大程度上提高了算法本身的安全性和抗攻擊性。

5 結語

研究了具有誤導功能的低冗余加密算法的安全性問題并進行了算法的改進，通過對擴充項和密鑰的處理，在不增加算法冗余的情況下增加算法的安全性。通過實驗驗證和結果分析，改進后的算法可以大幅度提高原有算法的安全性，通過對密鑰進行保護處理，使得密鑰的存儲更加安全可靠。