對2022年全國新高考數學Ⅱ卷第22題的探究
?海南省昌江黎族自治縣昌江中學 廖明艷 林瑞記 ?浙江杭州優才教育科技有限公司 李紅慶
1 高考試題呈現
(2022年全國新高考數學Ⅱ卷第22題)已知函數f(x)=xeax-ex.
(1)當a=1時,討論f(x)的單調性;
(2)當x>0時,f(x)<-1,求a的取值范圍;
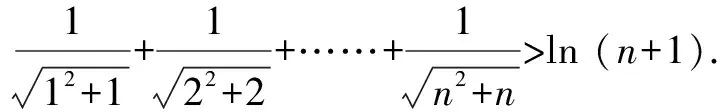
此題第(1)問難度較小易求解.筆者重點闡述第(2)(3)問的解題方法與邏輯分析.這兩問考查學生證明不等式的綜合能力,證明過程中會用到相關函數的性質,甚至需要學生自行構造新的函數,再推導題目中的不等式成立.
2 第(2)問的解法探析
針對第(2)問,具體解答思考過程的思維導圖如圖1所示:
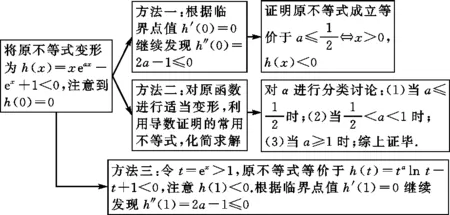
圖1
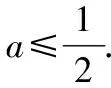
解法1:探求充分性,證明必要性.
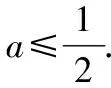
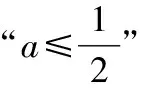
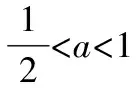
設φ(x)=ax+1-e(1-a)x,則有φ(0)=0,φ′(x)=a-(1-a)e(1-a)x.
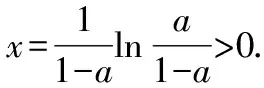
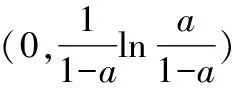
(iii)當a≥1時,存在x0=1,使得h(1)=ea-e+1>0,也不符合題意.
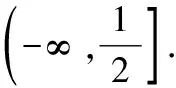
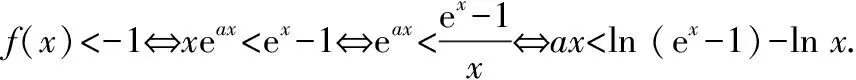

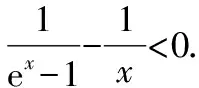
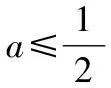
令φ(x)=(x-2)ex+x+2,則φ′(x)=(x-1)·ex+1,從而φ″(x)=xex>0,故φ′(x)在(0,+∞)上單調遞增.
所以,當x>0時,φ′(x)>φ′(0)=0,即φ(x)在(0,+∞)上單調遞增,則φ(x)>φ(0)=0,即h′(x)>0,從而h(x)在(0,+∞)上單調遞增.
因此,當x>0時,h(x)>h(0)=0.
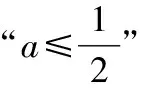
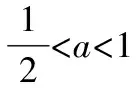
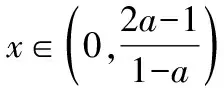
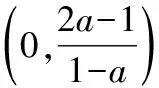
(iii)當a≥1時,存在x0=1,使得h(x0)=ln(e-1)-ln 1-a<0,不符合題意.
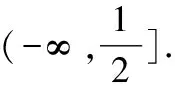
解法3:令t=ex>1,則x=lnt.當x>0時,f(x)<-1等價于當t>1時,f(lnt)<-1.
設h(t)=talnt-t+1<0.注意到h(1)=0,下面探求充分性.
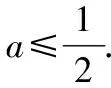
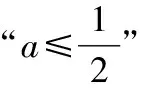
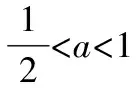
(iii)當a≥1時,由t>1易知h′(t)>0,所以h(t)在(1,+∞)上單調遞增,故存在t>1,使得h(t)>h(1)=0.
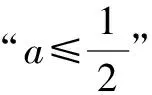
3 第(3)問的解法探析
針對第(3)問通過對不等式的整理與變換,將證明不等式恒成立的問題轉化為兩個數列求和比較的問題.具體解答思考過程的思維導圖如圖2所示:
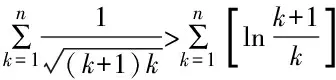
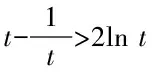
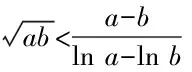
圖2
方法一:巧用賦值,化繁為簡.
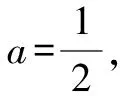
故所證不等式成立.
方法二:應用換元的方法,將問題簡化求解.
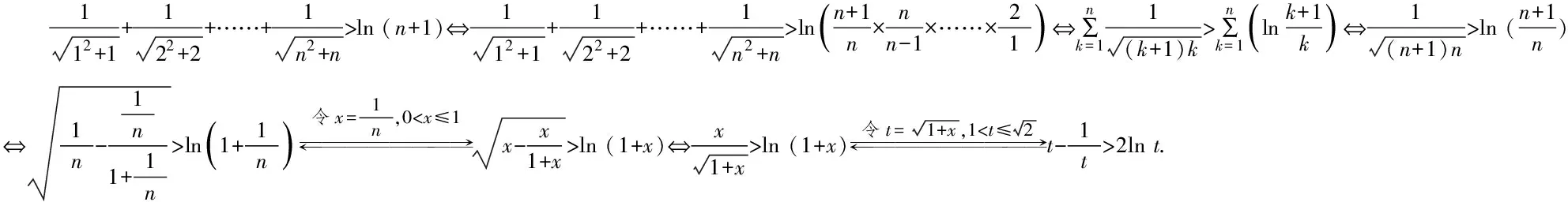
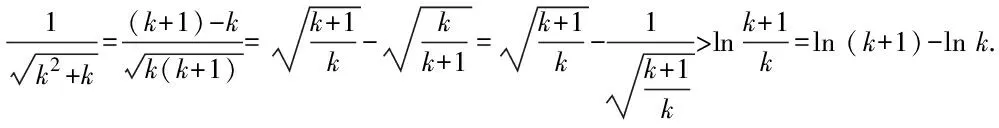
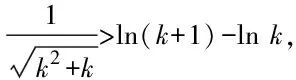
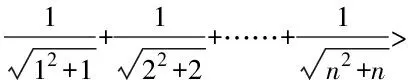
綜上可知,所證不等式恒成立.證畢.
方法三:應用對數均值不等式切入巧解秒殺.
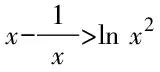
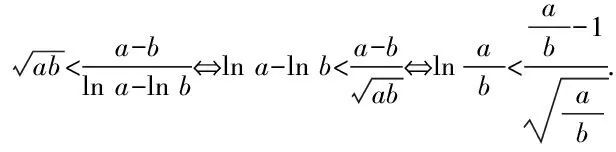
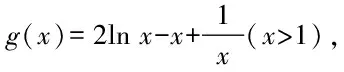
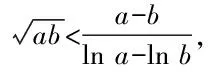
故原不等式得證.
2022年的全國新高考數學試卷突破了模擬試題的套路,試題呈現方式與解法都有創新.廣大數學教師要真正聚焦課堂教學,讓行之有效的學法、教法落實到位,繼續加強對命題及解題方法與策略的研究.

