圖形優美 思維精妙
——探究兩條拋物線相切的問題

?甘肅省張家川縣第一高級中學 李曉東

平時，我們經常遇到直線與拋物線相切的問題，也掌握了處理此類問題的常用方法.那么，當遇到一條拋物線與另一條拋物線相切時，該如何處理呢？實際上，可根據圖形特征，轉化為存在一條直線與兩條拋物線均相切；亦可根據切點的唯一性，轉化為相關方程有唯一解.下面結合一道試題的多解探究以及變式訓練，領會解題思維，提升解題技能.

1 好題采擷

(2021年廣東地區中科大強基測試第2題)設拋物線y=x2與x=ay2+1相切，則a=______.

分析:本題以兩條拋物線相切為載體，具有一定的創新性，看似簡單，實則內涵豐富；側重考查學生的數形結合能力、轉化能力、邏輯推理能力以及數學運算求解能力；有利于數學思想方法、知識在解題中的靈活運用，能夠較好地培養學生的探索精神、創新意識，提升學生的數學核心素養.

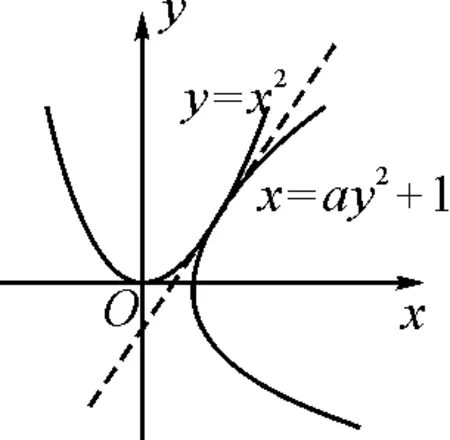
圖1

2 多解探究

如圖1，在同一坐標系內分別畫出拋物線y=x2與x=ay2+1(該拋物線顯然恒過定點(1,0)).根據題意易知a>0.(先確定參數的取值范圍，便于進一步分析.)

由圖可知，在兩條拋物線的公共點處，存在一條直線與兩條拋物線均相切.

視角一：由于題設兩條拋物線相切可轉化為存在一條直線與兩條拋物線均相切，又因為當直線與拋物線相切時，可考慮對應二次方程的判別式Δ=0在處理問題中的靈活運用，所以本題可充分利用“判別式為零”，并結合切點的坐標加以靈活分析.

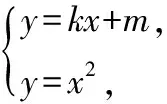
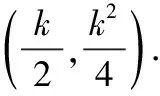
①

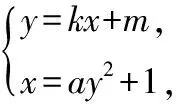
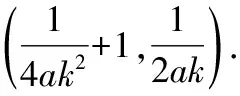
②

點評：該解法的關鍵是充分利用直線與拋物線相切，根據Δ=0巧求切點的坐標，突出體現了“方程思想”在解題中的靈活運用，對運算求解能力的要求較高.

視角二：由于題設兩條拋物線相切可轉化為存在一條直線與兩條拋物線均相切，又因當直線與拋物線相切時，可考慮導數的幾何意義在分析、解決問題中的靈活運用，所以本題可充分利用導數的幾何意義，并結合相關導數知識加以靈活分析.

解法2：依題意，對y=x2求導得y′=2x；對x=ay2+1求導得1=2ayy′.

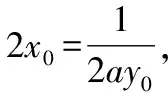
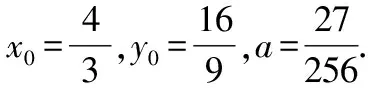
點評：解法2的關鍵是充分利用導數的幾何意義以及切點在拋物線上，構建等式.此外，要注意對x=ay2+1的求導，應靈活運用復合函數的求導法則.

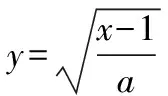
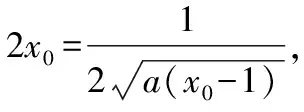
點評：解法3與解法2不同之處在于需要先轉化題設條件，以便能夠直接利用求導公式；同時要注意兩條拋物線在切點處的切線斜率相等及導數幾何意義的運用.

視角三：由于題設兩條拋物線相切可轉化為存在一條直線與兩條拋物線均相切，又因當直線與拋物線相切時，可考慮對應二次方程的判別式Δ=0與導數的幾何意義，所以本題可將“判別式為零”與“導數的幾何意義”在解題中同時加以靈活運用.

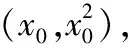
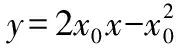
③

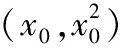
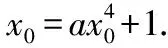
④

點評：解法4的關鍵是綜合運用了Δ=0和導數的幾何意義，同時要注意直線方程點斜式的運用.顯然，該解法對學生綜合運用能力的考查較強，有利于較好地培養學生的運算求解能力.

視角四：考慮“等價轉化思想”的靈活運用，可先將題設兩條拋物線相切轉化為關于x或者關于y的方程有唯一解，再結合其他知識加以靈活分析.

解法5：將y=x2代入x=ay2+1，可得

ax4=x-1.

⑤

依題意知方程⑤有唯一解，所以直線y=x-1與拋物線y=ax4必相切.

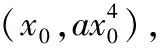
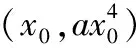
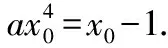
⑥

點評：解法5需要先將題設條件等價轉化為方程有唯一解，再等價轉化為直線與拋物線相切，最后借助導數知識和方程思想加以靈活求解.顯然，該解法突出考查了學生靈活運用“等價轉化思想”分析、解決目標問題的能力.

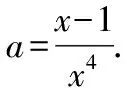
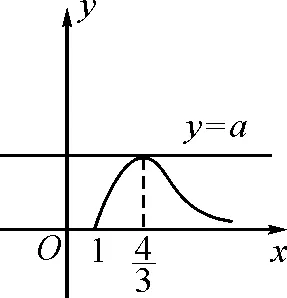
圖2

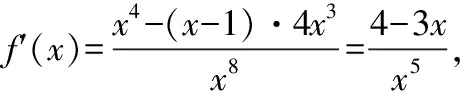
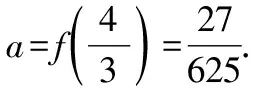
點評：解法6需要先將題設條件等價轉化為直線與函數的圖象有唯一公共點，再借助導數知識以及數形結合思想加以靈活求解，有利于較好地培養學生的數學核心素養.

3 變式訓練

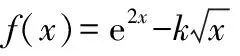
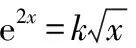
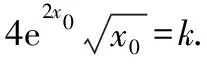
⑦

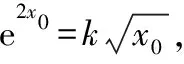
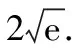
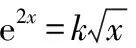
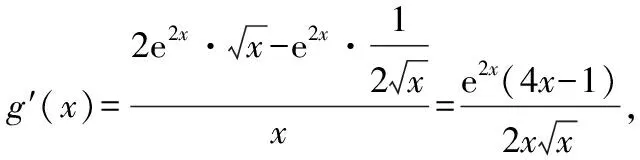
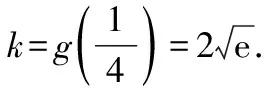
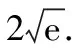
說明：有興趣的讀者可參考前述例題的多種不同解法，給出本題的其他解法.

綜上，處理兩條拋物線相切的問題，有多種不同的解題視角以及對應的具體解法.需要我們特別關注的是：(1)要學會以圖形的直觀、明了性作為分析、解決問題的切入點，便于幫助我們迅速獲得具體的解題思路；(2)要學會靈活運用“等價轉化思想”，將不熟悉的數學問題等價轉化為熟悉的數學問題，便于根據已掌握的知識、方法順利求解；(3)通過試題的多解探究以及變式訓練，努力提高直觀想象、數學運算、數學抽象以及邏輯推理等數學核心素養，進而提高分析、解決此類問題的技能技巧.

4 結語

一言以蔽之，小題不小，蘊含豐富，具有較好的思維價值、探究價值，值得我們去細細品味、深思；有利于提高學生對所學相關數學知識和思想方法的綜合運用能力，也有利于進一步拓寬視野，提高思維的靈活性、嚴謹性、邏輯性，進而提升理性思維能力.