離心率確定 多思維破解
——以2021年高考數學乙卷理科第11題為例
?廣東省信宜市信宜中學 梁北永
圓錐曲線(橢圓或雙曲線)離心率取值范圍的問題一直是高考的一個熱點問題.此類問題創新新穎,形式各樣,變化多端,難度較大.下面結合2021年高考數學乙卷理科試卷中的一道橢圓的離心率取值范圍的確定加以剖析與總結.
1 真題呈現
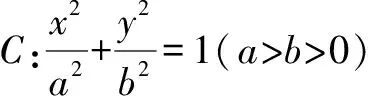
2 真題剖析
該題以橢圓為問題背景,借助橢圓上的動點所對應的線段長度的不等式恒成立來設置問題,簡單易懂.其實,類似的問題最早出現在2021年5月份東北三省三校(哈師大附中、東北師大附中、遼寧省實驗中學)高考數學三模數學試卷(理科)中:
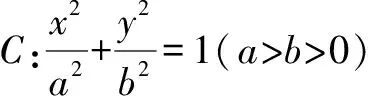
該問題與以上高考真題幾乎一致,都以選擇題的形式出現,題干基本一樣,選項有些許不同,所選結果也是一樣的.
3 真題破解
方法1:二次函數的圖象與性質法.
解析:由題意可得B(0,b).設P(x0,y0),則y0∈[-b,b].
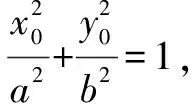
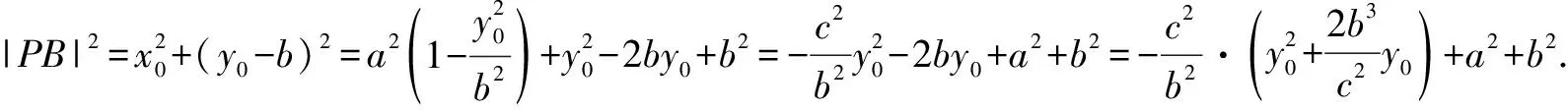
根據題目條件|PB|≤2b恒成立,則知當y0=-b時,|PB|2取得最大值(2b)2=4b2.
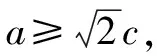
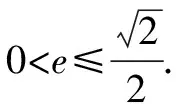
點評:設出動點P的坐標,根據其滿足橢圓方程進行合理變換,利用兩點間的距離公式,合理消參,轉化為含有參數y0的二次函數問題.根據題目條件中|PB|≤2b恒成立,轉化為二次函數的圖象與性質問題,建立對應的關系式.再利用橢圓離心率的公式以及取值范圍來分析與處理.合理轉化,把問題轉化為二次函數問題來處理,是破解此類問題最常用的基本方法之一.
方法2:橢圓與圓的位置關系法.
解析:由C上的任意一點P都滿足|PB|≤2b,則知以B(0,b)為圓心,2b為半徑的圓與橢圓至多有一個交點.
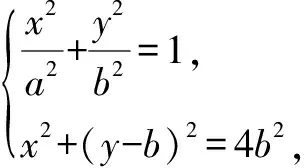
(a2-b2)y2+2b3y+3b4-a2b2=0.
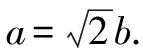
結合橢圓離心率e的幾何意義可知,當e→0時,此時橢圓越圓,滿足條件.
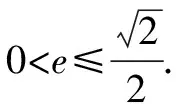
點評:根據題目條件中|PB|≤2b恒成立,轉化為對應的圓與橢圓的位置關系問題.通過聯立圓與橢圓的方程,消參轉化為含y的二次方程,利用判別式為0確定對應參數的關系,進而求解此時所對應的橢圓離心率.再利用橢圓離心率e的幾何意義確定離心率的取值范圍.等價轉化,結合圓與橢圓的位置關系,借助方程的判別式法來處理,思維巧妙.
方法3:三角參數法.
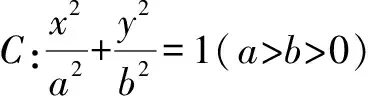
由于|PB|≤2b恒成立,則有a2cos2α+(bsinα-b)2≤4b2.
整理可得(a2-b2)sin2α+2b2sinα+3b2-a2≥0.
即[(a2-b2)sinα+3b2-a2](sinα+1)≥0.
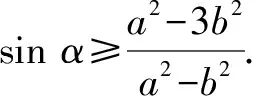
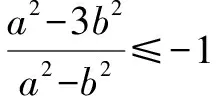
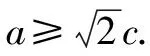
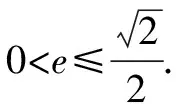
點評:根據點P是橢圓C上任意一點進行三角參數換元處理,結合題目條件中|PB|≤2b恒成立建立對應的不等式.通過十字相乘法加以因式分解,利用三角函數的圖象與性質,結合不等式恒成立加以轉化,建立含參的不等式問題.再利用橢圓離心率的公式以及取值范圍來分析與處理.通過三角參數進行換元處理,引入三角函數,借助三角函數的相關知識來分析與處理,也是一種非常不錯的破解方法.

圖1
方法4:數形結合法.
解析:由題意可得B(0,b),作出以點B為圓心,以2b為半徑的圓,如圖1所示.
設A為圓上任意一點,設∠ABO=θ(0≤θ<π),則知A(2bsinθ,-2bcosθ+b).
由C上的任意一點P都滿足|PB|≤2b,則知點A必在橢圓C外(包括橢圓上),即
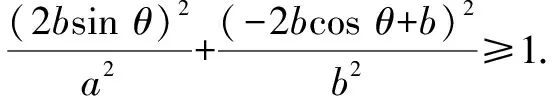
①
當sinθ=0時,①式顯然成立.
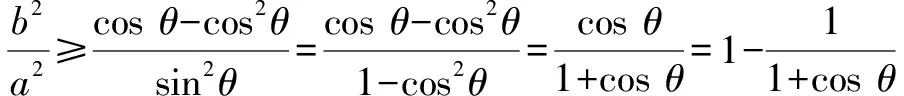
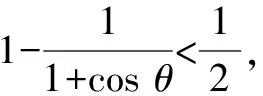
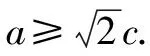
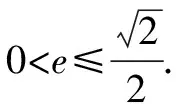
點評:根據題目條件作出以點B為圓心,以2b為半徑的圓,通過題目條件中|PB|≤2b恒成立,數形結合轉化為圓上任意一點A必在橢圓C外(包括橢圓上).結合點A坐標的確定并代入橢圓方程,分離系數轉化為三角函數關系式,結合不等式恒成立以及三角函數的取值范圍建立不等式,再利用橢圓離心率的限制條件來分析與處理.數形結合處理,直觀形象,合理轉化,巧思妙想,也是一種不錯的精彩解法.
4 教學啟示
破解圓錐曲線中離心率取值范圍問題的常見策略技巧:
(1)借助“題目條件”合理切入,直接利用題目條件中的不等信息建立對應的不等式(組),并利用圓錐曲線中離心率的取值限制條件加以綜合與應用.
(2)抓住“平面幾何”數形直觀,結合平面幾何圖形的基本性質,如三角形、圓等的基本性質,綜合圓錐曲線的幾何性質,數形結合,直觀想象.
(3)利用“三角參數”巧妙轉化,合理利用題目條件引入三角函數,將目標問題轉化為對應的三角函數問題,結合三角恒等變換以及三角函數的圖象與性質等來確定對應的取值范圍.
(4)結合“端點效應”進行特殊處理,根據圓錐曲線中在極端位置時所對應的離心率,通過“動”與“靜”的結合來確定離心率的取值范圍.
對于具體的圓錐曲線離心率的取值范圍問題,靈活應用,或一種策略獨領風騷,或多種策略齊心協力,或另辟蹊徑,合理轉化,巧妙破解.

