考慮執行器故障的無人帆船事件觸發控制

李紀強, 張國慶,*, 黃晨峰, 張衛東

(1. 大連海事大學航海學院, 遼寧 大連 116026; 2. 上海交通大學自動化系, 上海 200240)

0 引 言

無人帆船是目前的熱點研究問題之一,相比于傳統的欠驅動船舶,無人帆船能夠實現長時域值守任務,在海洋資源探索和環境監測方面具有重要應用。無人帆船依靠風能提供動力,在航行過程中由于受到不定常風的影響,會出現而頻繁操舵的現象,這在一定程度上增加了執行器的磨損。因此,有必要對無人帆船進行進一步的研究。無人帆船的艏向跟蹤控制是整個控制系統中的基礎技術,并且已經取得的了很多有益成果。文獻[4]對帆的空氣動力特性進行了研究,并且提出一種基于模糊邏輯的艏向跟蹤控制算法。無人帆船在航行過程中,帆結構不僅會提供前進的推力,還會產生橫向推力,這會造成船舶橫傾,嚴重時甚至會造成船舶傾覆。正是考慮無人帆船橫搖自由度的重要性,文獻[7]構建了一類具有龍骨板結構的帆船,采用分離型的思建立了四自由度數學模型,利用反步法技術設計了艏向跟蹤控制算法,并且通過數值仿真實驗驗證了控制方案的有效性。但是在所提控制器中,模型參數是被假設為已知的。為了解決工程實際問題并且提高控制器的簡捷性,神經網絡以及模糊邏輯系統(fuzzy logic system, FLS)已經被應用到船舶運動控制器設計中來逼近模型參數不確定問題。文獻[11]采用徑向基函數神經網絡(radius based function neural networks, RBF-NNs)對模型參數進行在線逼近,仿真結果表明自適應神經控制器具有良好的控制性能。文獻[12]針對無人帆船設計了魯棒自適應神經艏向跟蹤控制算法,盡管仿真結果驗證了該算法的有效性,但是在艏向跟蹤控制器設計中,假定無人帆船的轉船力矩主要由舵提供,帆、龍骨設備提供轉船力矩作為模型未知項被RBF-NNs逼近。事實上,帆結構會造成較大的轉船力矩,這一部分需要在控制器設計部分予以考慮。在現有的無人帆船艏向跟蹤控制算法中,主流的控制器設計方法是基于連續時間的反步法技術。

在實際海洋環境下,欠驅動船舶會因實時鎮定外界擾動造成的信號偏差發生控制輸入抖振現象。由于帆的存在,使得無人帆船更容易受到外界干擾并且控制輸入抖振更加頻繁。這會增加控制信號的傳輸負載和執行器的磨損程度,甚至會造成執行器故障。針對非線性嚴反饋系統,許多學者已經對事件觸發控制算法進行了較為深入的研究。在考慮執行器故障的情況下,文獻[18]針對非線性系統提出了一種基于模型的事件觸發控制算法,事件觸發規則被激活時,狀態變量、神經網絡自適應律同步更新。文獻[19]進一步提出了基于輸入端的事件觸發機制,僅當控制器輸入超出觸發閾值之后,控制器才會產生新的控制信號。這極大地降低了控制輸入的頻繁抖振,從而減少了執行器的磨損程度。文獻[20]將事件觸發技術引入到欠驅動船路徑跟蹤控制中,并對其進行了理論證明和數值仿真,驗證了事件觸發技術在智能航海領域的有效性。但是對于模型結構更為復雜的無人帆船的相關理論研究尚有不足。

基于以上分析,本文以無人帆船為研究對象,提出一種考慮執行器故障的事件觸發控制算法。采用RBF-NNs和動態面控制(dynamic surface control, DSC)對未知模型參數進行在線逼近和避免虛擬控制律求導帶來的“計算爆炸”問題。考慮帆結構造成轉船力矩的影響,在控制器設計中對其設計補償項,并且將執行器故障模型和事件觸發技術相結合,不僅降低了控制信號的傳輸負載,還避免了執行器故障帶來的系統不穩定現象。本文所提算法具有控制器形式簡捷、信號傳輸負載小、控制輸入抖振緩的優勢。最后,通過在4級/5級的海洋環境下進行仿真實驗,驗證了該算法的有效性和魯棒性。

1 基礎知識

1.1 無人帆船數學模型

文獻[7]根據分離型船舶運動數學模型的建模思想,把帆船整體受力分解,分析帆、舵、龍骨、船體4部分的受力從而建立帆船運動四自由度數學模型如下:

(1)

(2)

圖1 無人帆船姿態變量說明Fig.1 Illustration of unmanned sailboat attitude variables

無人帆船的轉船力矩主要由帆轉船力矩和舵轉船力矩決定,和可表示為

(3)

式中:僅作為控制器設計中舵轉船力矩的補償項,帆角控制策略參閱文獻[12];和分別為空氣和海水的密度;和分別表示帆和舵的面積;和分別表示帆的相對速度和舵的相對速度;()和()表示帆的升力系數和阻力系數;表示帆的攻角;表示帆的相對風角;表示帆索連桿的長度;表示舵中心距;和分別表示帆角和舵角。

無人帆船橫漂運動耗散有界穩定, 也就是橫漂速度存在上界。

假設風干擾具有慢時變特性,并且由平均風和擾動風構成。

1.2 徑向基函數神經網絡

RBF-NNs和FLS由于良好的非線性逼近能力,在工程領域具有廣泛的應用。本文采用RBF-NNs來在線逼近無人帆船的模型未知項。因此,引入以下引理。

()=()+

(4)

式中:=[,，…，]為權重矩陣;表示任意逼近誤差;()=[(),(),…,()]表示RBF函數基函數向量,()表示高斯函數:

(5)

式中:=1,2,…,;和分別表示高斯函數的中心值和標準差。

2 控制器設計

由式(1)和式(2)可寫出帆船艏向運動數學模型:

(6)

式中:

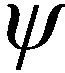
(7)

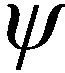
(8)

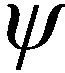
(9)

定義誤差變量=-,可得到:

(10)

(11)

為了避免對求導引起的“計算爆炸”問題,引入DSC技術,即

(12)

式中:為正的時間常數; 為動態面信號。定義DSC誤差= -。

對于式(6)中的非線性項(),采用RBF-NNs進行在線逼近,可以得到:

()=()+

(13)

由于外界海洋干擾以及連續時間系統的實時鎮定特性,會增加控制信號的傳輸負載以及執行器的磨損。文獻[19]提出的事件觸發技術確實會極大地降低控制信號的傳輸和執行器的磨損。但是也存在一個主要缺點,控制信號在保持不變時,可能存在系統偏離目標信號過大的情況。因此,本文設計了具有雙重保障的事件觸發機制,如下所示:

()=(),?∈[,+1)

(14)

觸發規則為

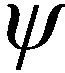
(15)

式中:()=()-();和表示觸發閾值參數;為誤差帶范圍。由式(15)可以得到:|()-()|≤||+。針對的正負號,有以下兩種情況。

如果≥0,可以得到--≤()-()≤+,進一步可以表述為

()-()≤(+),∈[-1,1]

(16)

如果<0,可以得到-≤()-()≤-+,進一步可以表述為

()-()≤(-),∈[-1,1]

(17)

根據情況1和情況2,可以得到:

(18)

式中:

=sign()=

(19)

基于以上分析,式(11)可以被表述為

(20)

式中:=(·)(1-)(1+)。

(21)

(22)

式中:,,,和表示正的設計參數。

3 穩定性分析

考慮到無人帆船數學模型式(1)和式(2),利用事件觸發規則式(15)、事件觸發控制律式(21)和自適應律式(22),可以獲得以下結果。

(1) 閉環系統內的所有信號滿足半全局一致有界(semi-global uniform ultimate bounded, SGUUB)穩定。

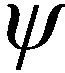
(3) 奇諾現象能夠被消除。

為了分析閉環控制系統的穩定性,構建李雅普諾夫函數如下:

(23)

對求導,可以獲得

(24)

為了進行下一步的放縮設計,利用楊氏不等式引入下式:

1999年，愛彼進入中國市場。在精簡的通路策略下，據統計，到2018年6月，愛彼目前在中國大陸僅設有6家專賣店。在這種情況下，如何利用合適的線上渠道，廣泛但精準的觸達更多中國新興中高產階級人群，是愛彼的第一層需求。

(25)

(26)

(27)

將虛擬控制律式(9)、事件觸發控制律式(21)、自適應律式(22)、式(25)和式(26)代入式(24),可以獲得

(28)

(29)

對式(29)兩端積分,可以得到:

(30)

事件觸發技術在控制系統中可能會產生奇諾現象,即在有限時間內發生無限次觸發。接下來,將會證明本文所提算法能夠有效地避免奇諾現象。觸發間隔+1-是正的常量,從式(14)和式(15)中,可以得到:

(31)

證畢

4 仿真實驗

為了驗證所提控制算法的有效性和魯棒性,本節通過Matlab仿真平臺,在基于機理模型的海洋環境下,以文獻[7]中提出的無人帆船(船長12 m,船寬3.21 m,舵面積1.17 m)為實驗對象進行了兩個仿真實驗。

4.1 模擬海洋環境

為了構建更加符合實際的海洋環境,本文以挪威石油工業組織規范(Norsk Sokkels Konkurranseposisjon, NORSOK)構建風干擾模型和聯合北海波浪計劃(Joint North Sea Wave Project, JONSWAP)構建風浪干擾模型。

風干擾可以分為平均風分量和干擾風分量,假設船體受風力作用中心距離海平面的高度為,則高度的平均風速可計算為

(32)

平均風速和平均風向的慢時變干擾特性可由1階高斯-馬爾可夫過程描述為

(33)

式中:1,2為高斯白噪聲;1,2為大于零的常量。

擾動風通常使用NORSOK譜構建簡諧波分量,并將其疊加,如下所示:

(34)

(35)

海浪干擾通常使用波譜進行構建和描述,在任一點處的波面函數可由描述為

(36)

式中:()表示簡諧波頻率密度譜;表示簡諧波頻率;表示隨機相位角;為波數。其具體推演過程可參閱文獻[28]。

假定主風向為10°,圖2和圖3給出4級和6級海況下的風速、風向和三維風生浪圖。

圖2 4級/6級海況下風速和風向歷時曲線Fig.2 Wind speed and direction under the fourth/sixth level sea state

圖3 三維風生浪圖Fig.3 3-D wind-generated waves

4.2 仿真實驗1

圖4 控制輸出對比Fig.4 Comparison of control output

圖5 控制輸入對比Fig.5 Comparison of control input

為了進一步量化控制效果,選取3個量化指標,即平均絕對跟蹤誤差(mean absolute tracking error, MATE)、平均絕對控制輸入(mean absolute control input, MACI)和平均控制輸入變差(mean control input variation, MCIV)。MATE描述閉環系統的穩定性,MACI描述閉環系統的控制性能,MCIV描述閉環系統的能量消耗平滑性,分別表示為

(37)

量化結果如表1所示。

表1 本文算法與文獻[7]和文獻[12]的量化對比結果

此外,為了驗證本文所提算法在傳輸負載方面的優勢,選取3個監測指標衡量閉環系統的性能,即消耗內存(consume memory, CM)、內存使用百分比(usage percentage, UP)和觸發數目(triggered number, TN)。CM和UP主要衡量控制系統的傳輸負載,TN表示控制系統采樣點數量。利用實驗用計算機(Inter Core(TM) i7-6800 HQ CPU @2.40 GHz, RAM:4.00 GB)測量系統性能,表2描述了本文所提算法與文獻[7]和文獻[12]的傳輸負載對比結果。

表2 本文算法與文獻[7]和文獻[12]的傳輸負載對比

4.3 仿真實驗2

為了進一步驗證本文所提控制算法的艏向跟蹤能力以及魯棒性,分別在4級和6級海況下進行艏向跟蹤仿真實驗。仿真時間為180 s,期望艏向設定控制器設計參數如下:

(38)

其他參數設置分別為=15,=10,=05,=08,=12,=18,=04,=001,=001。

圖6～圖9表示閉環控制系統在4級和6級海況下仿真實驗的主要結果。

圖6 艏向跟蹤控制效果Fig.6 Control effect of heading tracking

圖7 控制命令Fig.7 Control order

圖8 觸發時間間隔Fig.8 Trigger interval

圖9 自適應律Fig.9 Adaptive law

圖6為艏向跟蹤控制效果,可以看出兩種海況下,本文所提控制算法均能實現目標跟蹤,但是在6級海況下,艏向跟蹤精度較差。圖7表示無人帆船的控制命令信號,6級海況下,需要較大的控制命令補償帆結構引起的艏向偏差。圖8表示事件觸發時間間隔。從圖8中可以發現，4級海況下的觸發時間間隔大于6級海況下的觸發時間間隔，而且在6級海況下，無人帆船的觸發次數更多。圖9表示RBF-NNs權重自適應律和執行器自適應律,自適應律最終收斂到一定的界域內,滿足SGUUB的結論。

5 結 論

本文針對無人帆船在艏向跟蹤控制中存在的控制信號頻繁抖振、執行器故障以及帆結構產生的轉船力矩對艏向影響大的問題,提出了一種考慮執行器故障的無人帆船事件觸發控制算法。該算法中,利用DSC技術和RBF-NNs處理了虛擬控制律求導引起的“計算爆炸”和模型參數未知問題。通過設計執行器故障模型和事件觸發控制律避免了執行器故障帶來的系統不穩定現象,減少了控制輸入的頻繁抖振。借助李雅普諾夫穩定性判據,證明了閉環控制系統滿足SGUUB穩定,并且消除了由事件觸發技術引起的奇諾現象。最后,以12 m的無人帆船為控制對象,在Matlab平臺上進行仿真實驗,驗證了本文所提控制算法的有效性和魯棒性。