基于粒子群算法的改進模態參數識別方法

張錦東， 郭小農， 羅曉群， 張玉建， 徐洪俊,2

(1. 同濟大學 土木工程學院，上海 200092； 2. 國網江蘇省電力工程咨詢有限公司，南京 210000)

以研究結構動力特性為目標的振動模態參數識別方法是近年來工程領域的研究熱點之一。傳統的模態參數識別方法通常基于已知結構的輸入和輸出實現對模態參數的識別，此類方法受到現場試驗條件和結構規模的限制。相對地，另一類基于輸出的模態參數識別方法僅根據系統輸出進行模態參數識別，在交通、土木、機械、航空航天領域得到了廣泛的應用[1]。

基于輸出的模態參數識別方法在近幾十年來快速發展，環境激勵下的基于輸出的頻域[2]和時域[3-4]模態參數識別方法得到了廣泛的應用并取得了良好的效果，此類方法多用于激勵近似為白噪音或平穩激勵的情況。近年來，一類基于小波變換[5]或Hilbert變換的時頻分析方法被應用于基于輸出的結構模態參數識別中。Huang等[6]提出的經驗模態分解(empirical mode decomposition，EMD)和Hilbert-黃變換(Hilbert-Huang transform,HHT)實現了對復雜信號的瞬時特征提取以及對非平穩信號的分析，但是在處理密集模態結構的頻率混疊、窄帶信號以及信號間歇性波動等方面仍有不足。Chen等[7]提出的解析模態分解(analytical mode decomposition，AMD)與經驗模態分解具有相同的功能，并克服了經驗模態分解中存在的不足，在結構模態參數識別中得到一定應用，并成功進行了密集模態結構的模態參數識別[8]。

現有的基于Hilbert變換的結構模態參數識別方法通常將模態試驗中處理得到的多模態振動衰減信號進行分離，得到一系列時域單模態衰減信號后進行模態參數識別。此類方法中調用一次或多次Hilbert變換，存在邊界效應明顯、對噪聲敏感、邊界分割頻率對單分量信號的分離效果影響較大等問題。為此，本文結合奇異值分解、解析模態分解、自回歸功率譜和粒子群算法提出了一種可用于密集模態信號在強噪聲干擾下的改進模態參數識別方法。

本文首先介紹了基于粒子群算法的改進模態參數識別方法，并改變噪聲強度、頻率密集程度、阻尼比對模擬多模態振動衰減信號進行參數識別來驗證本文方法的有效性，最后采用本文提出的模態參數識別方法對數值模擬結構和實際結構進行模態參數識別。結果表明，本文提出的方法具有較高的識別精度，可實現在強噪聲干擾下的大阻尼、密集頻率信號的模態參數識別。

1 模態參數識別方法

1.1 奇異值分解降噪

結構模態參數識別前，對信號進行降噪以減小識別誤差。奇異值分解方法已被證明在信號降噪中是有效的，并且該方法可用于被白噪聲或者有色噪聲污染的信號降噪中。此方法的基本原理如下：

假設含有噪聲的信號如式(1)所示

y=[y1,y2,y3,…,yn]

(1)

基于相空間重構理論，將式(1)的信號構造為p×q階Hankel矩陣

(2)

式中，N為信號長度，N=p+q-1，且p≥q。

對Hm進行奇異值分解得到

Hm=UΣVT

(3)

式中，U和VT分別為p×p和q×q矩陣;Σ為式(4)所表達的p×q的對角矩陣

Σ=diag(λ1,λ2,…，λk)

(4)

式中，λ1,λ2,…,λk為矩陣Hm的奇異值，且λ1≥λ2≥…≥λk≥0。

采用奇異值分解降噪的關鍵問題是選定重構矩陣的維數和有效秩的階數。工程應用中通常取重構矩陣的維數p=N/2。土木工程結構的自振頻率在振動曲線的頻響函數中會出現明顯的峰值，根據此性質和文獻[9]的研究成果，對振動信號進行奇異值分解降噪時可取有效秩的階數等于源振動信號中主頻個數的2倍。

1.2 解析模態分解法

Chen等提出的解析模態分解在處理密集模態結構的頻率混疊、窄帶信號以及信號間歇性波動等方面比經驗模態分解具有更好的效果。該方法結合Hilbert變換實現了結構的模態參數識別和模態參數時變特性分析[10]，具有廣泛的應用空間。

0≤ω1<ωb1<ω2<ωb2…<ωi<ωbi<ωi+1…<ωn-1<ωb(n-1)<ωn

(5)

由此，原始信號x(t)可分解為一系列單頻信號，分解過程由式(6)和式(7)給出

si(t)=sin(ωbit)H[x(t)cos(ωbit)]-

cos(ωbit)H[x(t)sin(ωbit)],

(i=1,2,3,…,n-1)

(6)

(7)

式中，H[·]為Hilbert變換。

對多個密集頻率信號疊加的復雜信號進行模態分解時，解析模態分解法首先構造一對具有相同特定時變頻率的正交函數，并將該正交時變函數與原信號的乘積進行Hilbert變換，分解出在頻率時間平面內低于正交函數時變頻率的任意信號。利用AMD法可將多模態信號分解為一系列只含單模態特征的子信號。

在結構的模態試驗中，外界沖擊荷載激勵下多模態的自由衰減振動響應信號經解析模態分解后可被直接分解為一系列單模態自由衰減振動響應信號；環境激勵下的多模態振動響應信號經解析模態分解后可得到一系列單模態特征的子信號，此時可利用隨機減量技術消除子信號中隨機響應的影響，得到單模態自由衰減響應信號。

采用解析模態分解得到第j階模態的單頻信號xj(t)后，可構造解析信號yj(t)

yj(t)=xj(t)+iH[xj(t)]=Aj(t)·e-iθj(t)

(8)

通過式(8)可得到t時刻的振幅Aj(t)和相位θj(t)。

根據結構動力學理論可知，單模態自由振動衰減響應信號可表示為

A0e-ξjωjtcos(ωd,jt+φj)

(9)

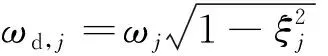
對比式(8)和式(9)，若令

θj(t)=ωd,jt+φj

(10)

則可根據解析信號yj(t)的瞬時相位函數θj(t)按式(11)得到結構第j階有阻尼固有頻率

(11)

同理，對比式(8)和式(9)，可構造對數函數

A(t)=A0e-αjt=A0e-ξjωjt

(12)

則可根據解析信號yj(t)的瞬時振幅函數Aj(t)，擬合得到對數函數A(t)的指數

αj=ξjωj

(13)

對于實際土木工程結構，阻尼比通常小于5%，因此采用有阻尼固有頻率ωd,j代替無阻尼固有頻率ωj能夠滿足計算精度要求，則結構的各階模態阻尼比為

ξj=αj/ωd,j

(14)

由于Hilbert變換導致端部的頻率泄露在式(12)的擬合過程中將產生明顯誤差，在式(5)～式(14)的模態參數識別過程中，Hilbert變換前可采用鏡像沿拓[11]抑制Hilbert變換產生的邊界效應。

1.3 自回歸功率譜

對于離散的振動信號而言，傳統的傅里葉變換存在頻譜泄露問題，信號中存在的噪聲或非平穩部分會導致傅里葉譜出現扭曲。此時可采用不涉及時頻轉化過程的參數化模型功率譜估計方法替代傅里葉譜。AR模型譜估計是功率譜估計的核心方法，采用AR模型譜代替傅里葉譜可更準確地確定功率譜峰值和解析模態分解的邊界分割頻率。將AR模型譜與小波變換[12]、解析模態分解[13]等結合，可明顯提升模態參數的識別精度。

采用式(15)所示的AR模型表示信號x(n)

(15)

(16)

則信號x(n)的自回歸功率譜PAR(ejw)可由式(17)計算

(17)

由于Burg法[14]通過分析觀測數據得到需要的模型參數，無需求解計算量較大的自相關函數，下文的AR模型譜估計使用Burg法。

1.4 粒子群算法

基于自回歸功率譜選取合理邊界分割頻率的前提下，采用式(5)～式(14)可較準確地分離信號、識別結構模態參數。實際結構的阻尼通常具有振幅相關性，在實測中不同的結構振幅將導致不同的阻尼比，因此實測振動信號的各單分量模態振動信號帶寬并不完全相同。對于阻尼比未知的密集頻率信號，解析模態分解中采用相對較窄的邊界分割頻率可能導致某階模態信號未完全被截取，而采用相對較寬的邊界分割頻率可能會截取到相鄰模態信號和較多噪聲信號。選取不合適的邊界分割頻率將導致分解出的時域曲線的形狀畸變，影響模態參數識別結果。針對此，采用粒子群優化(particle swarm optimization，PSO)算法AMD方法中的邊界分割頻率來得到最優化的振動衰減曲線，以進一步識別結構的自振頻率和阻尼比。

PSO-AMD的聯合模態參數識別方法如下。首先根據振動信號的自回歸功率譜圖采用峰值拾取法確定結構前D階有阻尼自振頻率ω=[ω1，ω2，…,ωD]T。然后建立一個D維搜索空間，該空間中有n個粒子組成的種群D=(D1,D2,…,Dn)。種群中的第i個粒子代表一個D維向量Di=[di1,di2,…,diD]T，該向量中的元素dij則代表第i個粒子中結構第j階模態的邊界分割頻率截斷帶寬。由此可確定AMD方法的邊界分割頻率可表示為

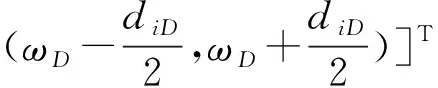
(18)

各粒子的適應度值可由解析模態分解分離所得的信號xj(t)和剔除此信號的其余信號xk(t)=x(t)-xj(t)的相關系數計算得出。若xj(t)被完全分離，則xj(t)和xk(t)的相關系數最小。每個粒子的適應度值均可表示為Ri=[Ri1,Ri2,…,RiD]T，該粒子的對應速度為Vi=[Vi1,Vi2,…,ViD]T，對應個體極值為Pi=[Pi1,Pi2,…,PiD]T，此種群的全局極值為Pg=[Pg1,Pg2,…,PgD]T。

迭代過程中，粒子更新速度和位置更新公式如式(19)和式(20)所示

(19)

(20)

式中：w為慣性權重；k為迭代次數；c為加速度因子；r為分布于[0,1]的隨機數。

盡管在密集頻率信號的模態參數識別中可以不斷人為調整AMD方法的截斷頻率分解出完整的單模態信號，得到準確的識別結果，然而由于事先并不確定最優化的邊界分割頻率，這類調整可能影響最終識別結果。將PSO方法與AMD方法結合，使邊界分割頻率可自適應地調整，從而提升識別效率和識別精度。

1.5 模態參數識別步驟

綜合1.1節～1.4節，對多模態振動衰減曲線的模態參數識別方法步驟如下：

步驟1根據振動曲線的自回歸功率譜確定振動信號的主頻數i和初始邊界分割頻率，根據主頻數確定奇異值分解階數2i，采用奇異值分解對信號進行降噪處理；

步驟2調用1.4節中的粒子群優化算法確定前j階單模態振動曲線的最優邊界分割頻率，優化目標為分離所得單模態信號與原信號中剔除該信號所得的信號相關度最低；

步驟3采用步驟2中的最優邊界分割頻率調用解析模態分解法獲取單模態衰減曲線并進行模態參數識別，獲取結構前j階阻尼比、自振頻率。

基于Hilbert變換的模態參數識別方法對噪聲敏感，較強的噪聲影響模態參數的識別結果。受外界環境的干擾，實際模態試驗中采集的信號信噪比可能較低，識別效果不佳。本文提出的方法理論上可實現低信噪比下白噪聲或有色噪聲信號的降噪，將PSO方法和AMD方法結合可自適應地對邊界分割頻率進行調整，提升模態參數識別精度。

2 模擬信號模態參數識別

結構模態試驗中一類常見的測試方法是對結構施加一定的激勵后獲取結構的自由衰減振動響應，對自由衰減振動曲線進行模態參數識別。為了驗證本文提出的模態參數識別方法的有效性，構造式(21)所示的振動衰減信號進行模態參數識別

(21)

下文分別改變噪聲強度、頻率密集程度和信號阻尼比，采用了三種方法進行信號的模態參數識別：方法1——僅采用解析模態分解法進行信號分離，對單模態信號進行識別，邊界分割頻率按Chen等的研究取兩個主頻信號的二分位置；方法2——利用粒子群算法優化邊界分割頻率后，采用解析模態分解法進行信號分離，對單模態信號進行識別；方法3——采用本文提出的模態參數識別方法進行模態參數識別。

2.1 不同噪聲強度下模態參數識別

按照式(21)形式給出一條包含三個主頻、時長為50 s、采樣頻率100 Hz的模擬振動衰減信號(單位mV)，模擬振動衰減信號的主要參數，如表1所示。在此衰減信號中加入不同強度的白噪聲，使信噪比(signal-to-noise ratio,SNR)分別為-6 dB，-2 dB，2 dB，6 dB，10 dB。圖1中僅展示在-6 dB信噪比下振動衰減時程曲線、自回歸功率譜和采用方法3分離的單模態衰減振動曲線。

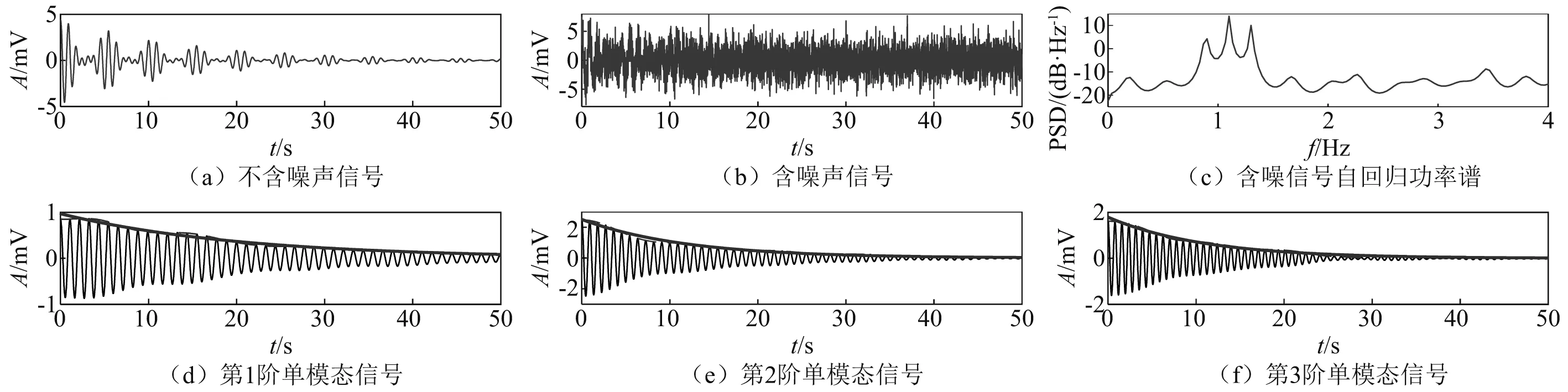
圖1 原信號和單模態信號Fig.1 Original signal and single mode signal

表1 模態參數理論值Tab.1 Theoretical values of modal parameters

采用方法1、方法2、方法3識別得到的自振頻率和阻尼比識別結果，如表2所示。自振頻率和阻尼比的識別誤差折線圖，如圖2所示，圖例中1-2代表采用方法1對第2階模態參數的識別誤差，依次類推。圖2中，三種方法對自振頻率的識別結果誤差均保持在5%以內；方法1和方法2在信噪比小于-2 dB時對阻尼比的識別產生了超過10%的誤差，較強的噪聲影響了單模態信號的分離效果；方法3在信噪比為-6 dB的強噪聲環境中仍保持了較高的阻尼比識別精度。在信噪比大于6 dB時三種方法的識別誤差相近。

表2 模態參數識別結果Tab.2 Identification results of modal parameters

圖2 模態參數識別誤差Fig.2 Error of modal parameter identification

對圖1(a)的振動衰減信號添加有色噪聲，驗證在有色噪聲干擾下本文方法的識別效果。有色噪聲由強度為20 dB的高斯白噪聲ξ1(n)和幅值為2 mV的白噪聲ξ2(n)按式(22)組合而成

(22)

將式(22)的有色噪聲加入表1的振動衰減曲線中，有色噪聲信號、含色噪聲信號、自回歸功率譜和方法3分離的單模態衰減信號，如圖3所示。對含有色噪聲的衰減信號識別結果和誤差，如表3所示。表3中，方法3自振頻率和阻尼比的識別誤差均小于5%，在較強有色噪聲干擾下本文提出的方法依然可以較好地實現模態參數的識別精度。

圖3 原信號和單模態信號Fig.3 Original signal and single mode signal

表3 模態參數識別結果Tab.3 Identification results of modal parameters

2.2 不同阻尼比下模態參數識別

保持振動衰減信號的自振頻率f、初始振幅A0和相位φ與表1相同；并在信號中加入高斯白噪聲，保持信號信噪比為2 dB。分別取各階模態阻尼比為0.5%，1%，2%，3%，4%，以驗證不同阻尼比下模態參數識別效果。限于篇幅，圖4中僅展示在模態阻尼比為4%時的振動衰減時程曲線、自回歸功率譜和采用方法3分離的單模態衰減振動曲線。

圖4 原信號和單模態信號Fig.4 Original signal and single mode signal

采用方法1、方法2、方法3的自振頻率和阻尼比識別結果，分別如表4和表5所示。自振頻率和阻尼比的識別誤差折線圖，如圖5所示，圖中1-2代表采用方法1對第2階模態參數的識別誤差，依次類推。圖5中，三種方法對自振頻率的識別誤差相差不大，均保持在4%以內。隨著阻尼比的增加，各個方法對于阻尼比的識別誤差均呈現增大趨勢，這是由于振動曲線衰減較快導致擬合衰減曲線的數據點不足。相對而言，本文提出的方法3對于阻尼比識別精度高于方法1和方法2，誤差保持在5%以內。當衰減信號阻尼較大(>3%)時，方法3也可較準確地識別大阻尼衰減信號的模態參數。

表4 自振頻率識別結果Tab.4 Identification results of natural frequency

表5 阻尼比識別結果Tab.5 Identification results of damping ratio %

圖5 模態參數識別誤差Fig.5 Error of modal parameter identification

2.3 不同頻率密集度下模態參數識別

在振動衰減曲線中加入高斯白噪聲，保持信號信噪比為2 dB，判斷不同頻率密集度下模態參數識別效果。頻率密集度δ=(fi-fi-1)/(fi+fi-1)[15]。衰減曲線的各階自振頻率和阻尼比，如表6所示，初始振幅A0和相位φ與表1相同。圖6中僅展示在δ=0.03時的振動衰減時程曲線、自回歸功率譜和采用方法3分離的單模態衰減振動曲線。

表6 模態參數理論值Tab.6 Theoretical values of modal parameters

圖6 原信號和單模態信號Fig.6 Original signal and single mode signal

采用方法1、方法2、方法3的自振頻率和阻尼比識別結果，如表7所示。自振頻率和阻尼比的識別誤差折線圖，如圖7所示，圖中1-2代表采用方法1對第2階模態參數的識別誤差，依次類推。圖7中，當頻率較為密集時，兩個模態間的相互影響作用增強，各個方法的分離效果下降，誤差增加，隨著頻率密集程度的減小，自振頻率和阻尼比的識別誤差減小。本文提出的方法在密集度δ=0.03時對自振頻率和阻尼比的識別誤差仍保持在4%以內，實現了較準確的識別。

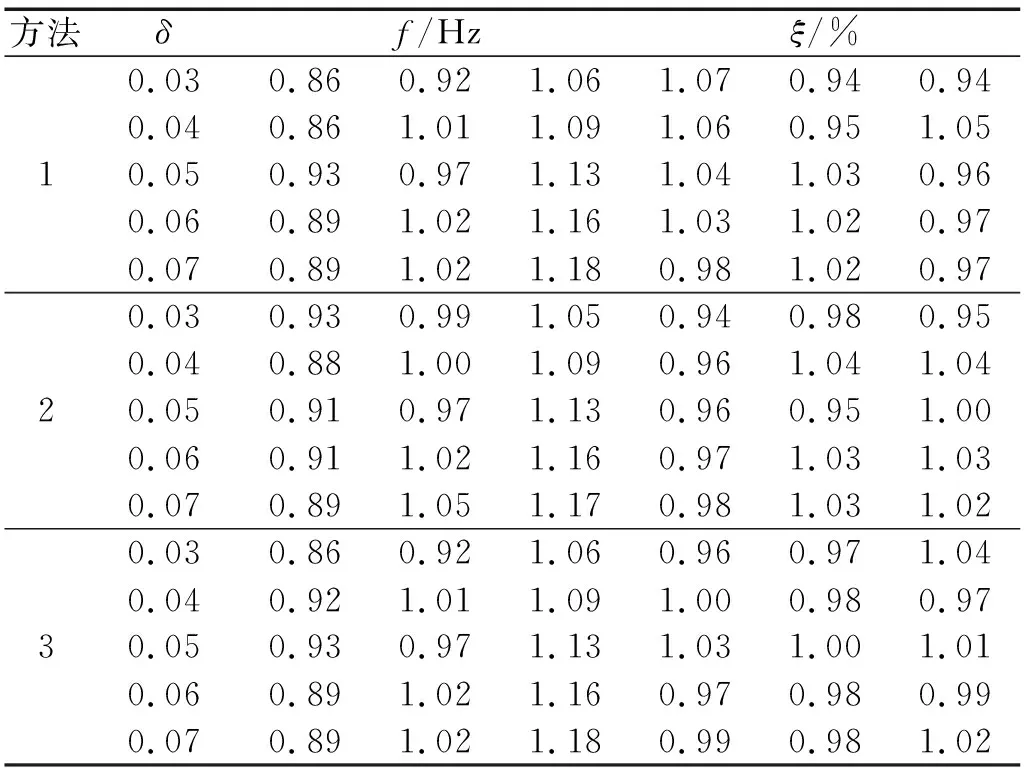
表7 模態參數識別結果Tab.7 Identification results of modal parameters

圖7 模態參數識別誤差Fig.7 Error of modal parameter identification

3 結構模態參數識別

3.1 三自由度系統模態參數識別

建立一個圖8所示的三自由度彈簧-質量系統，彈簧剛度和質點質量如表8所示。數值模擬采用有限元分析軟件ANSYS19.0，采用Rayleigh阻尼模擬系統的阻尼特性，Rayleigh阻尼系數α=0.010 62，β=0.002 04。在0時刻對質點3施加1 000 kN的沖擊荷載，并在響應曲線中加入式(22)形式的有色噪聲，其中高斯白噪聲ξ1(n)強度為-150 dB，白噪聲ξ2(n)幅值為10-6m/s2。質點1的有噪聲響應曲線、自回歸功率譜、前3階單模態響應曲線，如圖9所示。

圖8 三自由度彈簧-質量系統Fig.8 Three degree of freedom spring-mass system

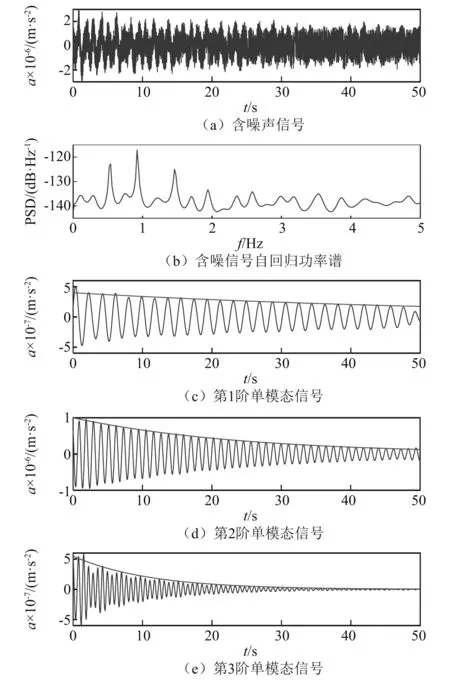
圖9 原信號和單模態信號Fig.9 Original signal and single mode signal

表8 彈簧剛度和質點質量Tab.8 Spring stiffness and mass of particles

三自由度彈簧-質量系統自振頻率與阻尼比的理論值、識別值和識別誤差(以Ef和Eξ表示)如表9所示。表9中，自振頻率和阻尼比的識別誤差≤2%，本方法在較大有色噪聲干擾下仍取得了較好的識別效果。

表9 模態參數識別結果Tab.9 Identification results of modal parameters

3.2 球面空間網格結構模態參數識別

對圖10所示的球面空間網格結構進行激勵并采集節點的振動響應。測試人員在節點跳躍對結構施加近似的豎向沖擊荷載，同時采集節點的豎向振動響應。激勵點位置和采集點位置,如圖11所示。測試中，在A1點施加豎向激勵，同時在1點采集節點響應，依次進行至在A10點施加豎向激勵，同時在10點采集節點響應，共采集10條振動衰減曲線。由于測試中外界環境和結構附加設備的運行對結構造成影響，采集到的振動衰減響應曲線信噪比較低，采用本文的模態參數識別方法對響應曲線進行識別。

圖10 球面空間網格結構Fig.10 Spherical reticulated spatial structures

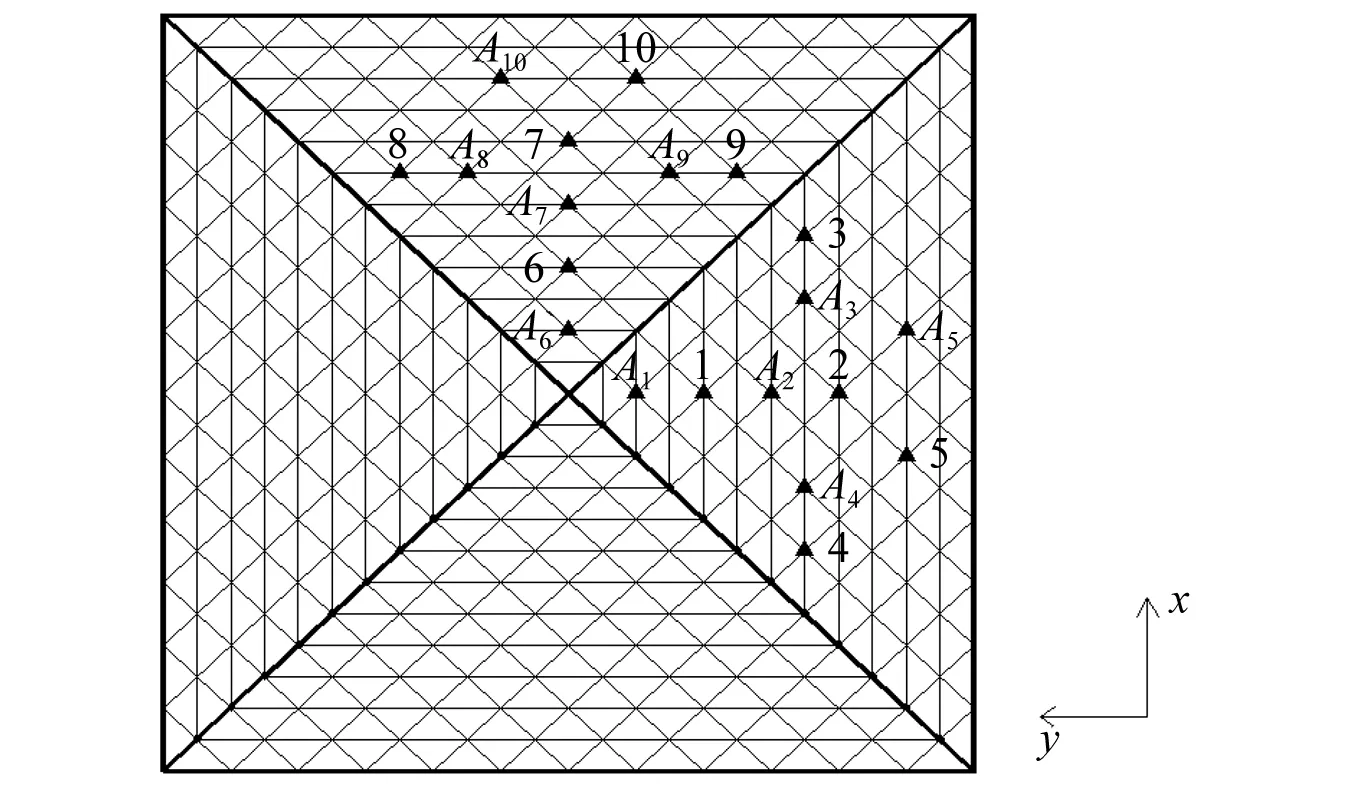
圖11 激勵點和采集點Fig.11 Excitation positions and collection positions

采集點1處的振動響應曲線、自回歸功率譜、采用本文模態參數識別方法得到的結構前6階單模態響應曲線，如圖12所示。依次對10條振動衰減曲線進行識別，各振動衰減曲線的前6階自振頻率和模態阻尼比如表10所示。表11給出了文獻[16]中此結構的前6階自振頻率和模態阻尼比均值，采用本文方法識別的自振頻率均值和模態阻尼比均值同時列于表11。表11中本文方法的識別結果與羅曉群等的識別結果基本一致，本文方法可在較低信噪比下識別密集頻率結構的自振頻率和阻尼比。

表10 曲線1～10模態參數識別結果Tab.10 Modal parameter identification results of curve 1-10

表11 模態參數識別結果均值Tab.11 Mean value of modal parameter identification results

4 結 論

本文針對多模態振動衰減信號的模態參數識別，提出了一種基于粒子群算法的改進模態參數識別方法，改善了現有的基于Hilbert變換的模態參數識別方法存在的邊界效應明顯、對噪聲敏感、邊界分割頻率對單分量信號的分離效果影響較大等問題，可用于強噪聲干擾下密集頻率、大阻尼信號的模態參數識別，并通過數值算例和現場測試驗證了本文提出方法的有效性。得到結論如下：

(1) 現有的基于解析模態分解的傳統方法僅可實現較高信噪比條件下(>6 dB)的模態參數識別，本文提出的識別方法可實現在低信噪比(-6 dB)、有色噪聲環境下的模態參數準確識別，具有更廣泛的應用范圍。

(2) 隨著阻尼比增加，振動曲線衰減較快導致擬合衰減曲線的數據點不足，基于衰減曲線的識別方法對阻尼比的識別精度呈現下降趨勢，將信號準確分離是實現具有較大阻尼比衰減信號的模態參數識別的關鍵。

(3) 隨著頻率密集度的增加，各模態的相互影響作用增強，阻尼比和自振頻率的識別精度呈現下降趨勢。邊界分割頻率明顯影響密集頻率信號的模態參數識別效果。本文提出的方法可尋找最優邊界分割頻率，將各單模態信號準確分離和識別。

(4) 本文提出的方法可用于低信噪比環境下結構的模態參數識別。