單自由度碰撞振動系統的奇異非混沌動力學和多穩態共存

吳 鑫， 李高磊， 樂 源

(西南交通大學 力學與工程學院，成都 610031)

具有懸臂結構的碰撞系統作為一類典型的非光滑系統，已廣泛應用于航空航天、機械制造、電子器件等工業領域[1-3]。通常，非光滑系統中的非光滑因素來源于系統間隙、碰撞或干摩擦等。而具有懸臂結構的碰撞振動系統則同時具有懸臂結構彎曲產生的幾何非線性因素和碰撞所產生的非光滑因素，其累積效應通常會使系統產生更加復雜的動力學現象[4]。目前，對懸臂碰撞振動系統的研究主要集中在系統的諧波共振、分岔和混沌等動力學行為方面[5-7]。目前尚無關于懸臂碰撞振動系統的奇異非混沌動力學方面的相關研究。

奇異非混沌吸引子(strange nonchaotic attractors, SNAs)是奇異但非混沌的吸引集，其通常產生于擬周期運動與混沌運動之間。“奇異”指的是吸引子具有分形的幾何結構。“非混沌”指的是吸引子不依賴于系統的初始條件，即最大Lyapunov指數為非正數。從Grebogi等[8]在1984年首次揭示SNAs以來，人們認識到“奇異”并非等價于“混沌”，并在各類非線性動力系統中通過理論、數值和試驗等方法對SNAs進行了廣泛的研究。目前奇異非混沌動力學已經成為動力學領域重要的研究課題之一。

Ding等[9]從數值和解析的角度證實了SNAs在擬周期系統中的存在，并舉例說明了在典型的擬周期系統中可能出現的多種動力學行為。Pikovsky等[10]利用SNAs對外激勵相位具有敏感依賴性，通過計算相敏感指數來刻畫吸引子的奇異性。Nishikawa等[11]利用不變曲線的泛函方程研究了一類SNAs在擬周期激勵系統中的分形及混沌演化。Witt等[12]通過研究受擬周期激勵Logistic映射的周期3窗口的內部激變，發現了由內部激變導致SNAs產生的新機制。Ditto等[13]在研究受雙頻擬周期激勵的屈曲磁彈性帶的試驗中，首次證實了SNAs的存在。Thamilmaran等[14]通過試驗方法在LCR電路系統發現了產生SNAs的三種路徑，即Heagy-Hammel路徑、分形路徑和陣發路徑。Chithra等[15]在三階混沌電路系統中發現了混沌吸引子及奇異非混沌吸引子，并通過最大Lyapunov指數、功率譜和0-1測試方法對兩種吸引子進行了區分。Lindner等[16]利用開普勒太空望遠鏡記錄了天琴座內一些恒星的亮度在主頻率和次頻率上波動的光線曲線，這兩種頻率的比率接近于黃金分割值，而由次頻率驅動的非線性動力系統通常存在SNAs，這是實驗室外首次證實SNAs的存在。

上面的研究對象多數是針對光滑系統。目前已經有研究發現在碰撞類非光滑系統中也存在豐富的奇異非混沌動力學現象。Zhang等[17]研究了一類剛性約束碰撞振動系統在余維三分岔點附近由于環面倍化中斷而產生的SNAs。Yue等[18]通過研究周期激勵的三自由度對稱碰撞振動模型，在系統余維二分岔點附近發現存在SNAs，并進一步討論了SNAs與混沌吸引子等的共存情況。

在實際工程中，具有懸臂結構的碰撞振動系統有時處于復雜的外部環境中。通常，可用多頻激勵來近似模擬系統在外荷載作用下的振動碰撞，當各激振頻率不可有理通約時，則可以視為系統受擬周期激勵[19]。本文在以上研究基礎上，建立一類受擬周期激勵的具有懸臂結構的碰撞振動非光滑模型，揭示了其奇異非混沌動力學以及多穩態共存現象。通過相敏感性、奇異連續譜和有理數頻率逼近以及狀態變量的傅里葉變換的部分和在復平面上的路徑等工具刻畫了吸引子的奇異性；并利用最大Lyapunov指數[20-22]描述了吸引子的非混沌性。研究發現此類非光滑系統中SNAs的兩種不同演化路徑及其與擬周期吸引子及混沌吸引子共存的多穩態現象。

1 含懸臂結構碰撞振動系統的動力學模型

含懸臂結構碰撞振動系統的動力學模型，如圖1所示。質量為M的質量塊連接在兩根懸臂結構的自由端，懸臂結構簡化為兩片板式彈簧，不計質量，長度為L，抗彎剛度為EI(E，I分別為懸臂結構的彈性模量和截面慣性矩)。質量塊受到F1=A1cos(ωt)和F2=A2cos(φt)的激勵力作用，e1和e2為質量塊與彈簧約束面之間的間隙。以系統靜止時質量塊上邊緣為坐標原點，豎直向下為正方向，建立直角坐標系。當質量塊的位移為e1或-e2時，將會與上下兩個彈性約束面發生碰撞。

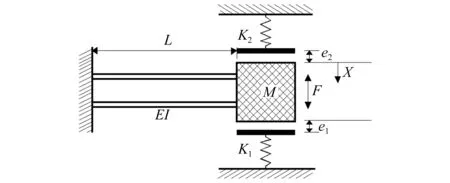
圖1 含懸臂結構碰撞振動系統的動力學模型Fig.1 Dynamic model of vibro-impact system with cantilever

單自由度含懸臂結構碰撞振動系統的的運動微分方程為

(1)

式中：f(X)為懸臂結構的彈性恢復力，其可以描述為非線性形式

(2)

E(X)為間隙分段函數，其表達式為

(3)

引入無量綱量，式(1)可轉化為

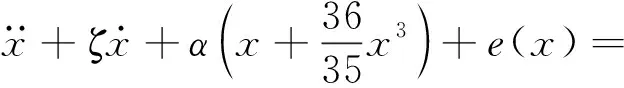
(4)

其中，

(5)

令θ=ωt，φ=φt，將式(4)在相空間R2×T2中寫成如下形式

(6)

通過角度變量φ引入三維Poincaré映射

Π:Σ→Σ,
Σ≡{(x,v,θ)∈R×R×S1|φmod 2π=0}

(7)

則映射方程可表示為

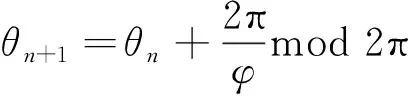
(8)

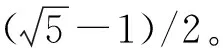
2 吸引子奇異性驗證

2.1 相敏感函數

由于映射式(8)在區間θ=[0 2π]上稠密，所以其SNAs是不分段可微的。SNAs對系統初始條件的改變不具有敏感性，這反映在其最大Lyapnuov指數為非正數。然而，其對外激勵的相位卻具有敏感依賴性。基于此可以通過研究吸引子對相位的導數來刻畫吸引子的奇異性。吸引子對相位的導數為

(9)

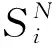
相敏感函數可以通過計算SNAs的時間序列而獲得。對于任意小的ε，存在于滿足相位差ε0=|θn0-θ0|<ε的n0，則吸引子對相位的導數又可近似表示為

(10)

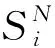
(11)

2.2 奇異連續譜

奇異連續譜法是在研究擬周期晶格模型和受擬周期激勵的量子系統中首次提出。通常，動力系統的功率譜具有三種狀態：周期或擬周期等常規運動對應的離散功率譜、混沌或隨機運動對應的連續功率譜、奇異非混沌運動對應的奇異連續譜。因此，通過對吸引子進行譜分析可以驗證吸引子的奇異性。

系統狀態變量x的傅里葉變換部分和可表示為[23]

(12)

式中：Ω與系統兩個激勵力的頻率之比成比例關系； 當T為時間時，X(Ω,T)為復平面上(ReX,ImX)上的路徑。通常，X(Ω,T)與T存在以下冪率關系

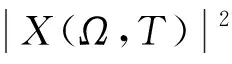
(13)

式中，ρ為標度因子。若系統吸引子為SNAs，則1<ρ<2，且X(Ω,T)在復平面(ReX,ImX)上的路徑具有分形自相似結構。

2.3 有理數頻率逼近

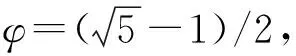
φk=Fk-1/Fk，Fk=1,1,2,3,5,8,…

(14)

式中，Fk為斐波納契數。則系統無理數頻率可以表示為極限形式

(15)

通過以上變換，原擬周期系統轉換為周期系統。

3 奇異非混沌吸引子

抗彎剛度作為懸臂結構的重要力學參數之一，對其深入研究具有重要理論及現實意義。對于本系統，當系統質量塊質量和懸臂結構長度確定后，則無量綱參數α可視為系統懸臂結構的抗彎剛度系數。因此，對系統抗彎剛度的研究可轉換為對系統參數α的研究。下面研究均以系統參數α為控制參數。

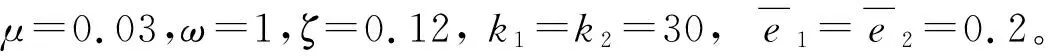
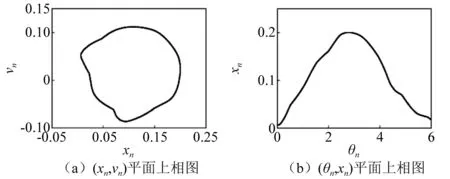
圖2 α=0.620，1T環面Fig.2 For α=0.620，1T tours

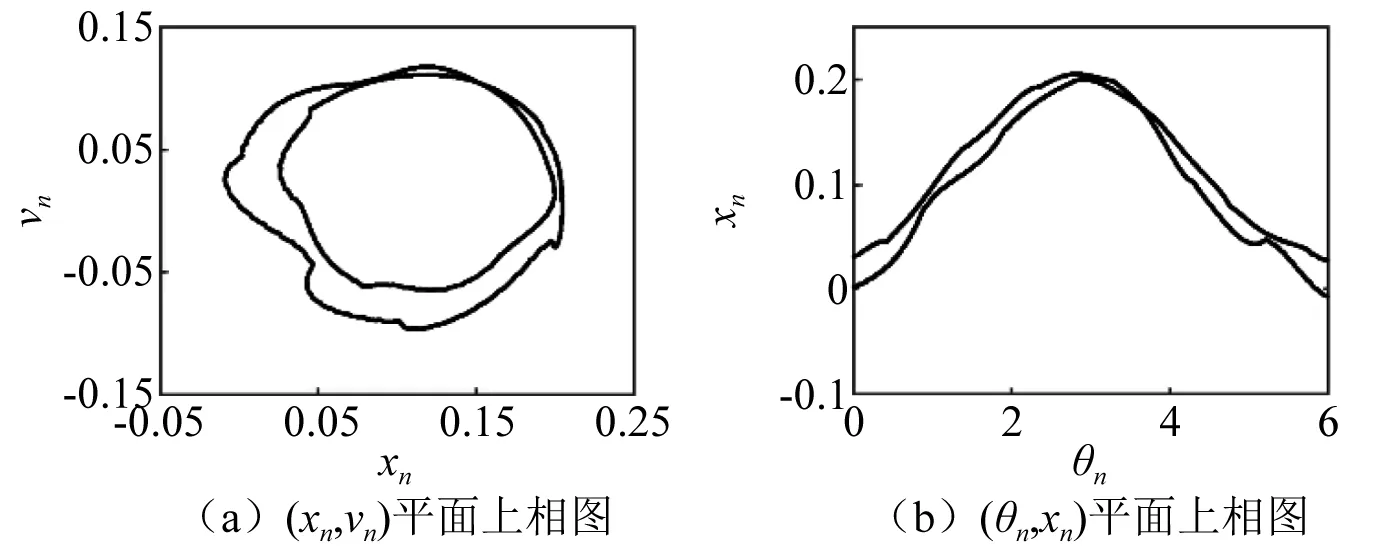
圖3 α=0.610，2T環面Fig.3 For α=0.610，2T tours

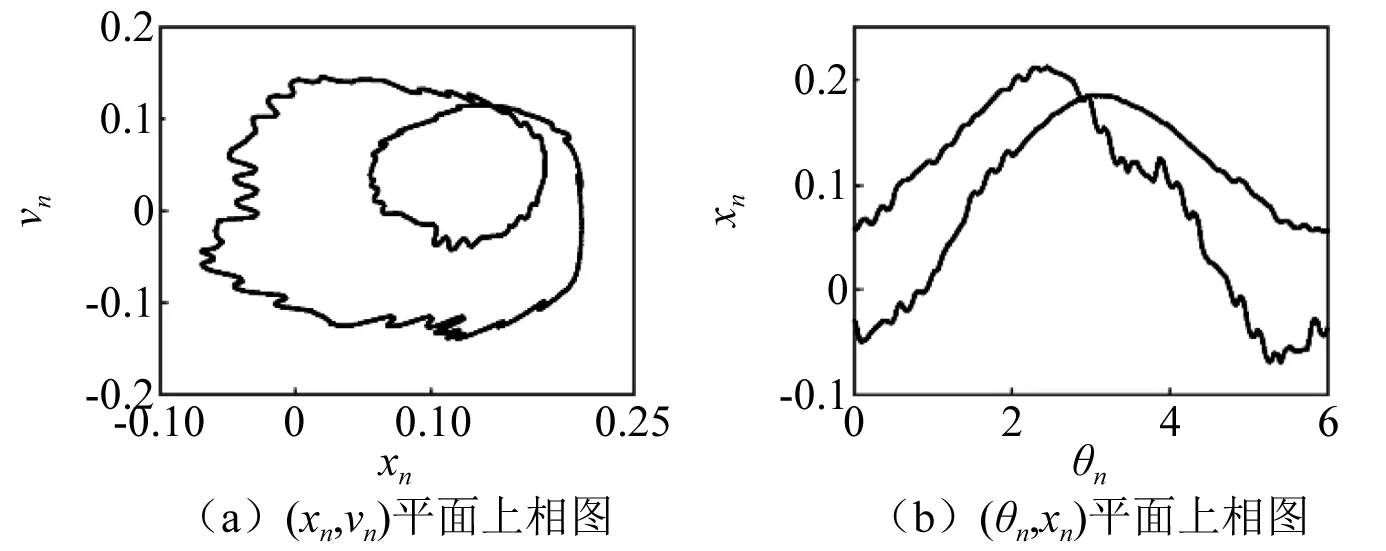
圖4 α=0.59，2T環面Fig.4 For α=0.59，2T tours

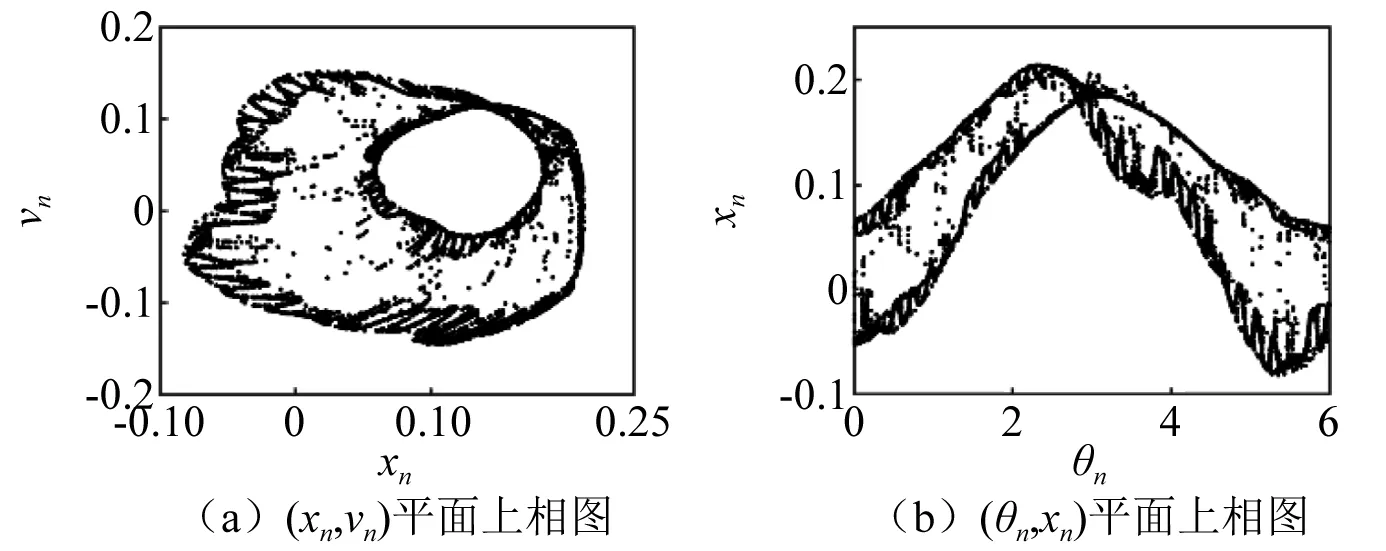
圖5 α=0.587 7，SNAFig.5 For α=0.587 7，SNA

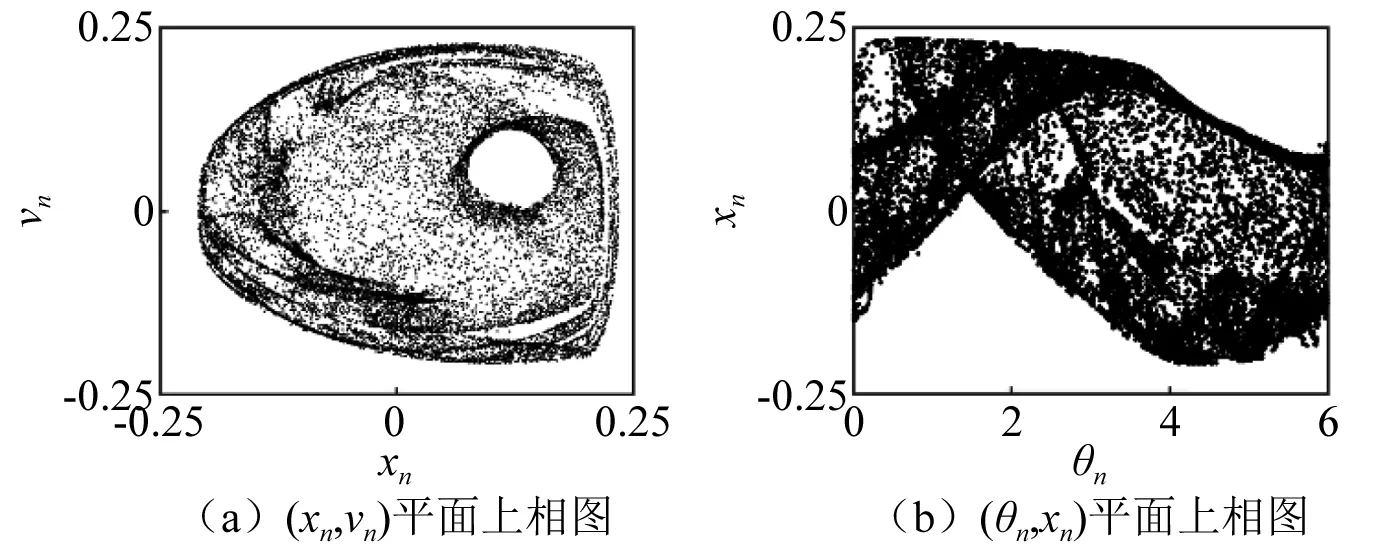
圖6 α=0.56，混沌吸引子Fig.6 For α=0.56，chaotic attractor

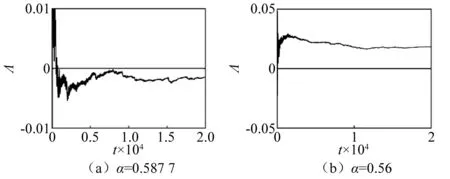
圖7 最大Lyapunov指數譜Fig.7 Top Lyapunov exponent

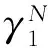
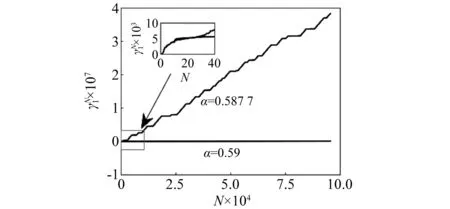
圖8 α=0.59, α=0.587 7時相敏感函數Fig.8 Phase sensitivity function when α=0.59, α=0.587 7

當α=0.587 7時系統的奇異連續譜，如圖9(a)所示。由圖9(a)可見，此時標度因子β=1.28；X(Ω,T)在復平面(ReX,ImX)上的路徑圖像，如圖9(b)所示。可以看出其具有明顯的分形結構，這也表明了吸引子的奇異性。

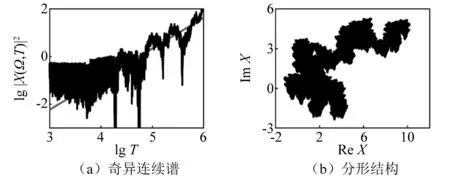
圖9 α=0.587 7時的奇異連續譜和分形結構Fig.9 Singular continuous spectrum and fractal structure when α=0.587 7

圖10為當近似階數為φk=144/233，φk=6 765/10 946時近似系統在(θn,xn)平面上對應的相圖，對比圖5和圖10可以看出，當近似階數增加時，近似系統的吸引子進一步逼近原系統的吸引子，這再一次證實了α=0.587 7時系統吸引子的奇異。

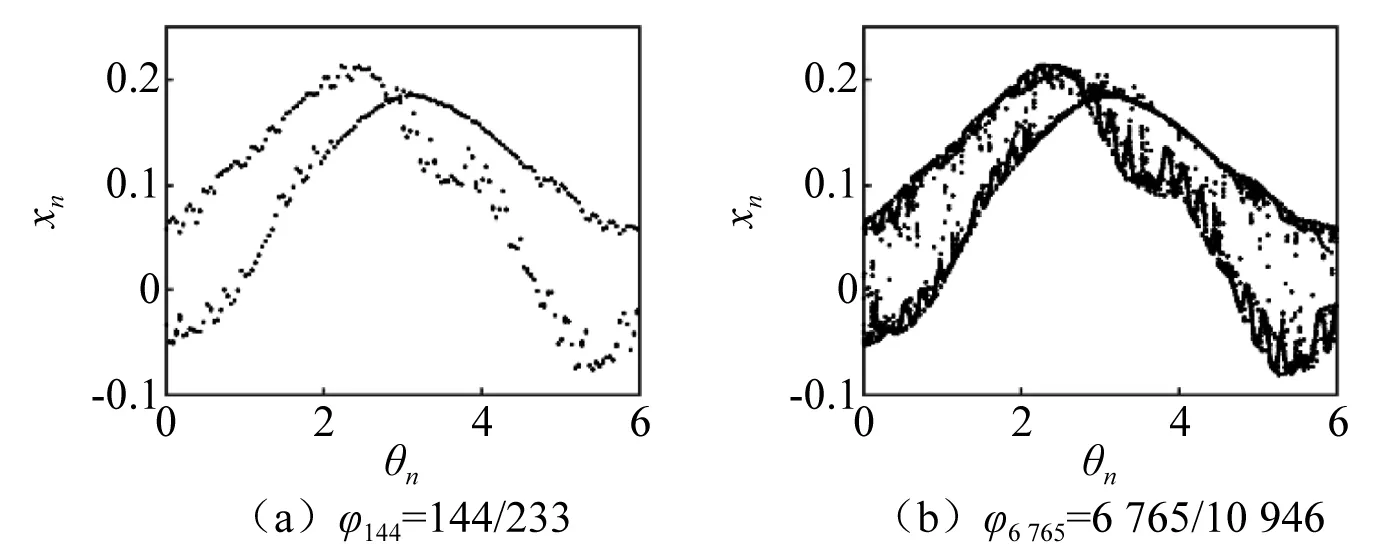
圖10 α=0.587 7時有理數頻率逼近Fig.10 Rational frequency approximation when α=0.587 7

4 奇異非混沌吸引子的產生機制

4.1 分形路徑

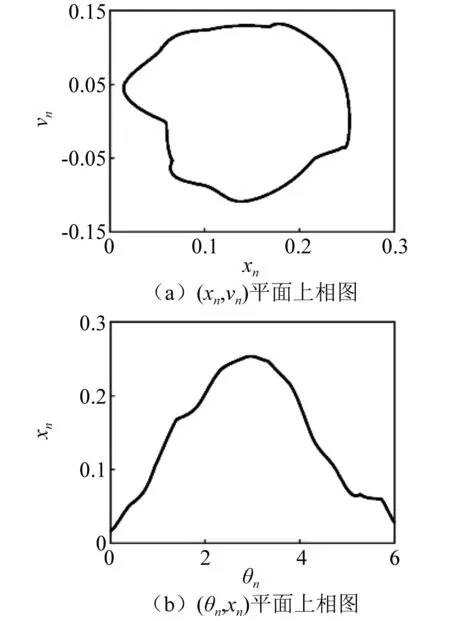
圖11 α=0.615，1T環面Fig.11 For α=0.615，1T tours

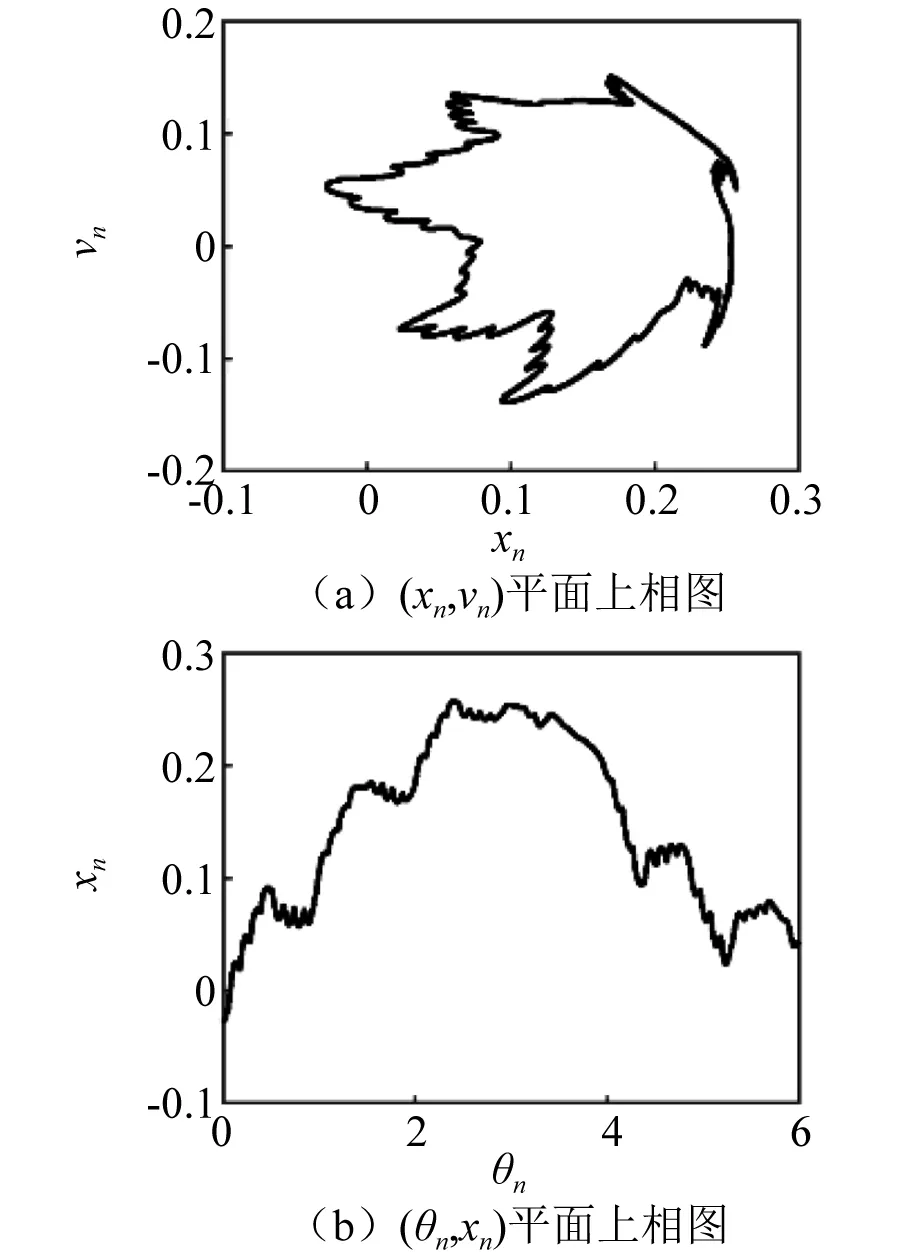
圖12 α=0.605，1T環面Fig.12 For α=0.605，1T tours

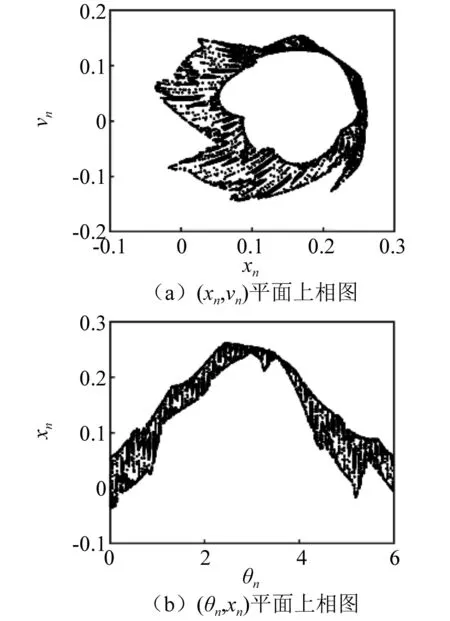
圖13 α=0.600 5，SNAFig.13 For α=0.600 5，SNA

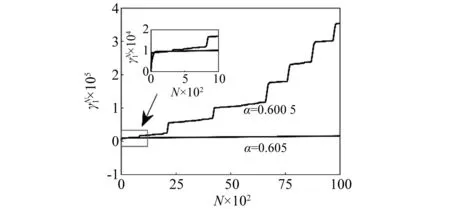
圖14 α=0.605, α=0.600 5時相敏感函數Fig.14 Phase sensitivity function when α=0.605, α=0.600 5

圖15 α=0.600 5時的奇異連續譜和分形結構Fig.15 Singular continuous spectrum and fractal structure when α=0.600 5

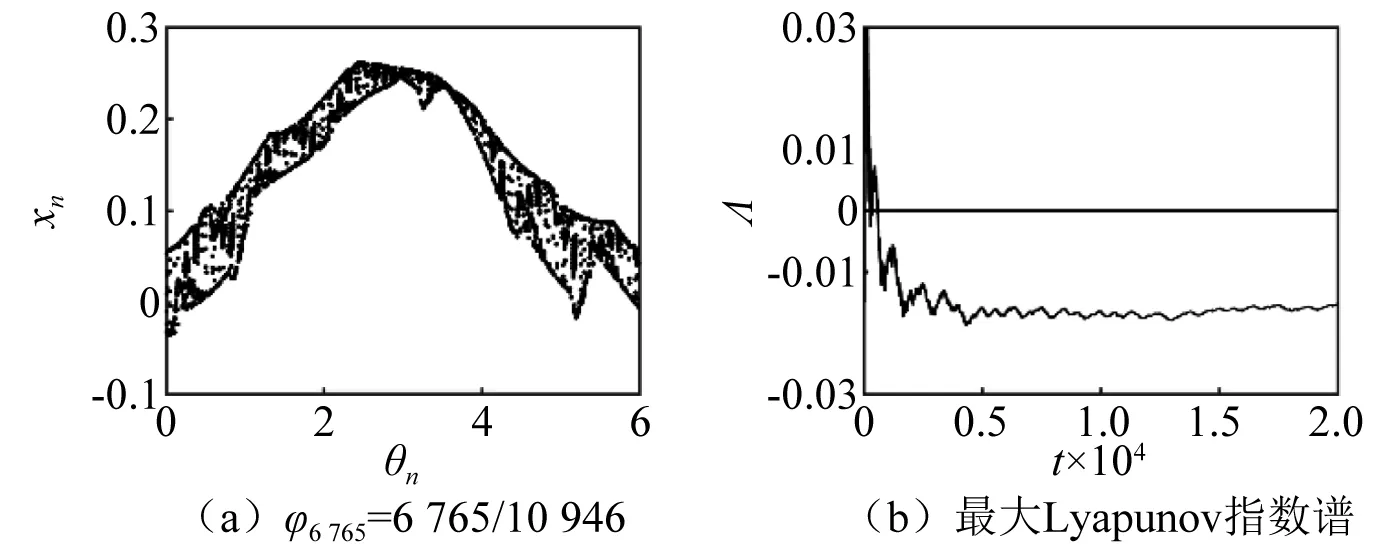
圖16 α=0.600 5時的有理數頻率逼近和最大Lyapunov指數譜圖16 Rational frequency approximation and top Lyapunov exponent when α=0.600 5

4.2 陣發路徑

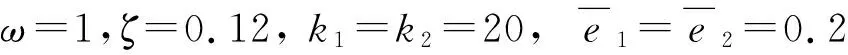
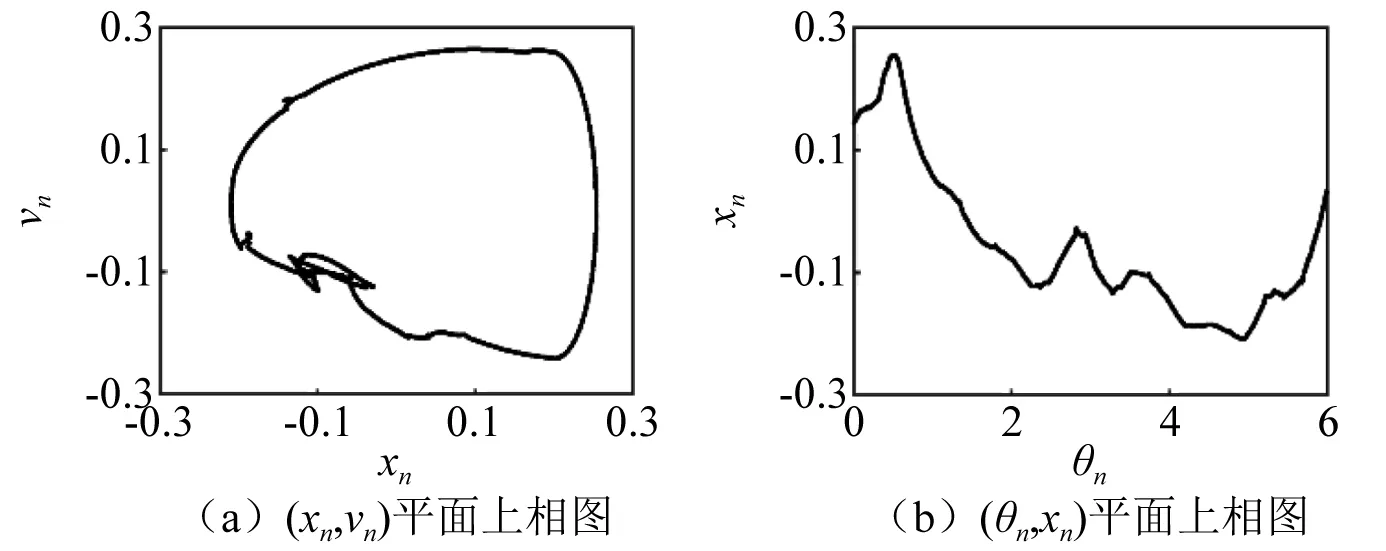
圖17 α=0.59，1T環面Fig.17 For α=0.59，1T tours

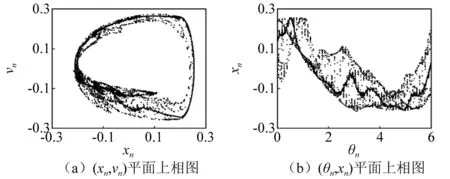
圖18 α=0.587，SNAFig.18 For α=0.587，SNA

SNAs的奇異性同樣通過相敏感性、奇異連續譜和有理數頻率逼近的方法進行刻畫。通過系統相敏感函數描述系統在此參數條件下吸引子的奇異性，如圖19所示。圖20(a)為α=0.587時吸引子的奇異連續譜，可以看出SNA的奇異連續譜呈現出很強的冪率行為，此ρ=1.50，同時X(Ω,T)在復平面(ReX,ImX)上的路徑也具有明顯分形特征，如圖20(b)所示。圖21(a)為取近似階數φ6 765=6 765/10 946的有理數逼近，其與圖18(b)中的結構相似。

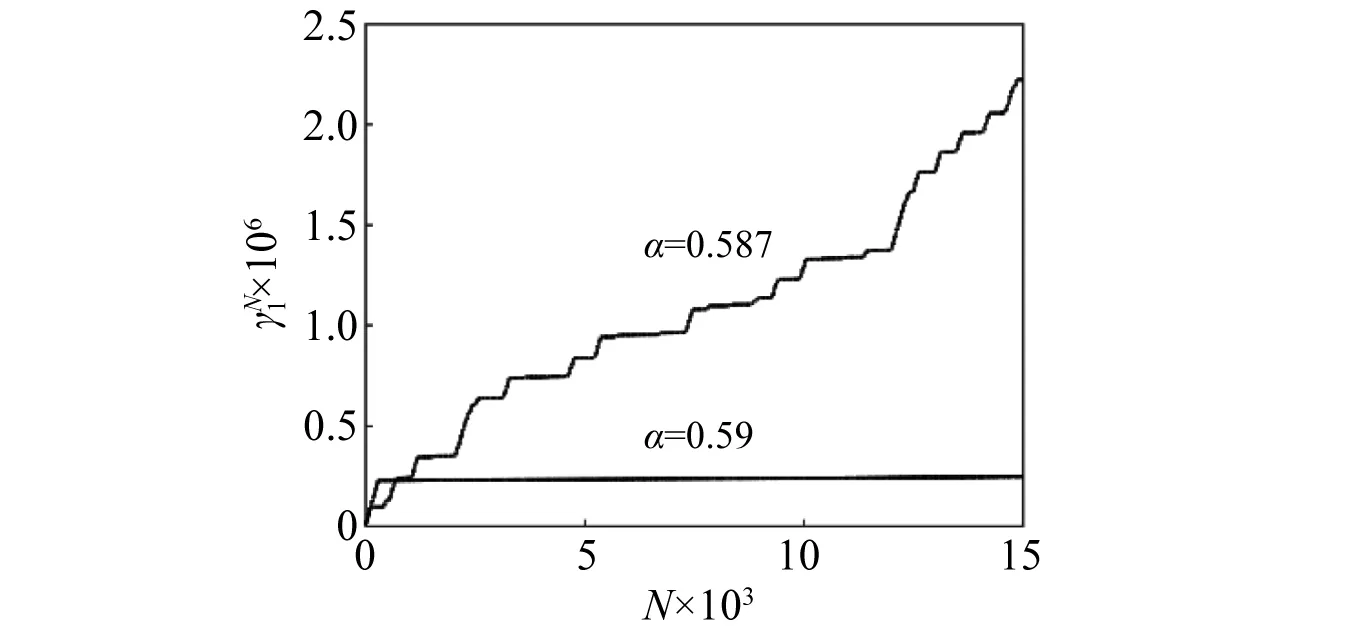
圖19 α=0.587時相敏感函數Fig.19 Phase sensitivity function when α=0.587

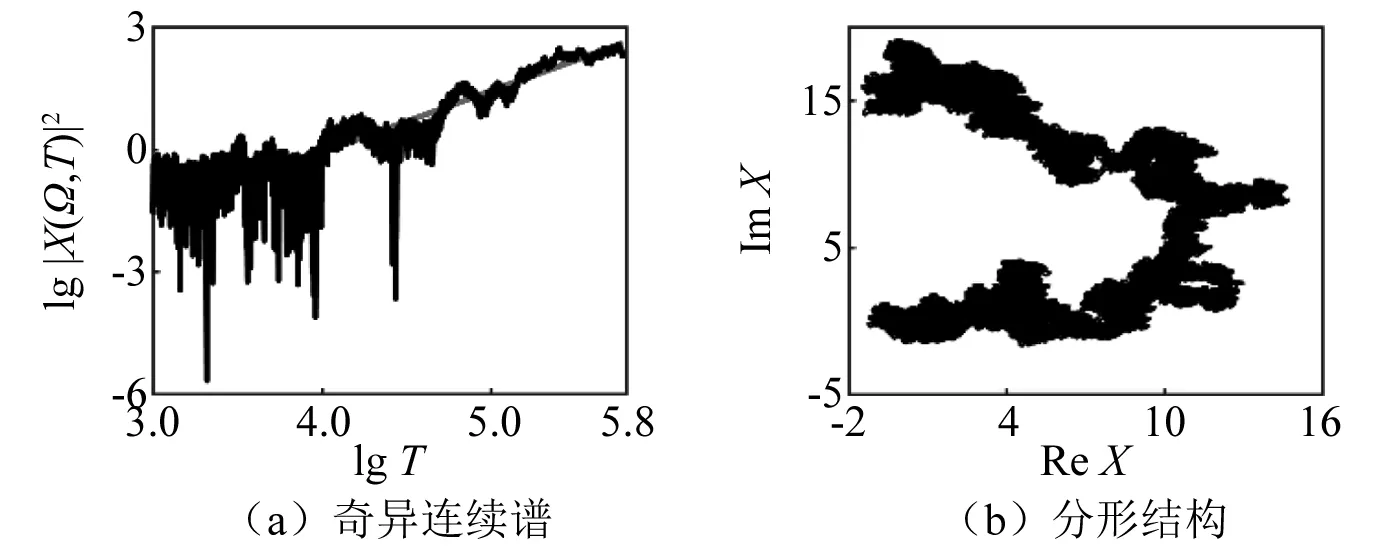
圖20 α=0.587時奇異連續譜和分形結構Fig.20 Singular continuous spectrum and fractal structure when α=0.587

在圖21(b)中，系統最大Lyapunov指數收斂于負值，表明了此時吸引子的非混沌性。

圖21 α=0.587時有理數頻率逼近和最大Lyapunov指數譜Fig.21 Rational frequency approximation and top Lyapunov exponent when α=0.587

5 奇異非混沌吸引子的多穩態動力學

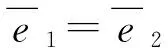
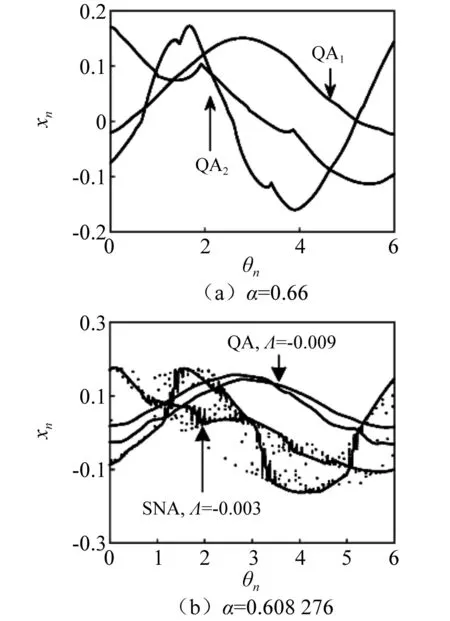
圖22 (θn,xn)平面上相圖Fig.22 Phase diagrams in (θn,xn)

當α進一步減小到0.608 27時，系統的穩態SNA演化為暫態SNA。由圖23(a)可見，當初始條件為(0.15,0.15)時，系統隨時間的演化由奇異非混沌運動轉變為擬周期運動，圖23(b)為初始條件為(0,0)時系統狀態變量v的時間序列。不同時間區域內系統在(θn,xn)上的相圖，如圖24所示。由圖24(a)可見，在[0,30 000]時間區域內，系統T-SNA與2T擬周期吸引子共存。

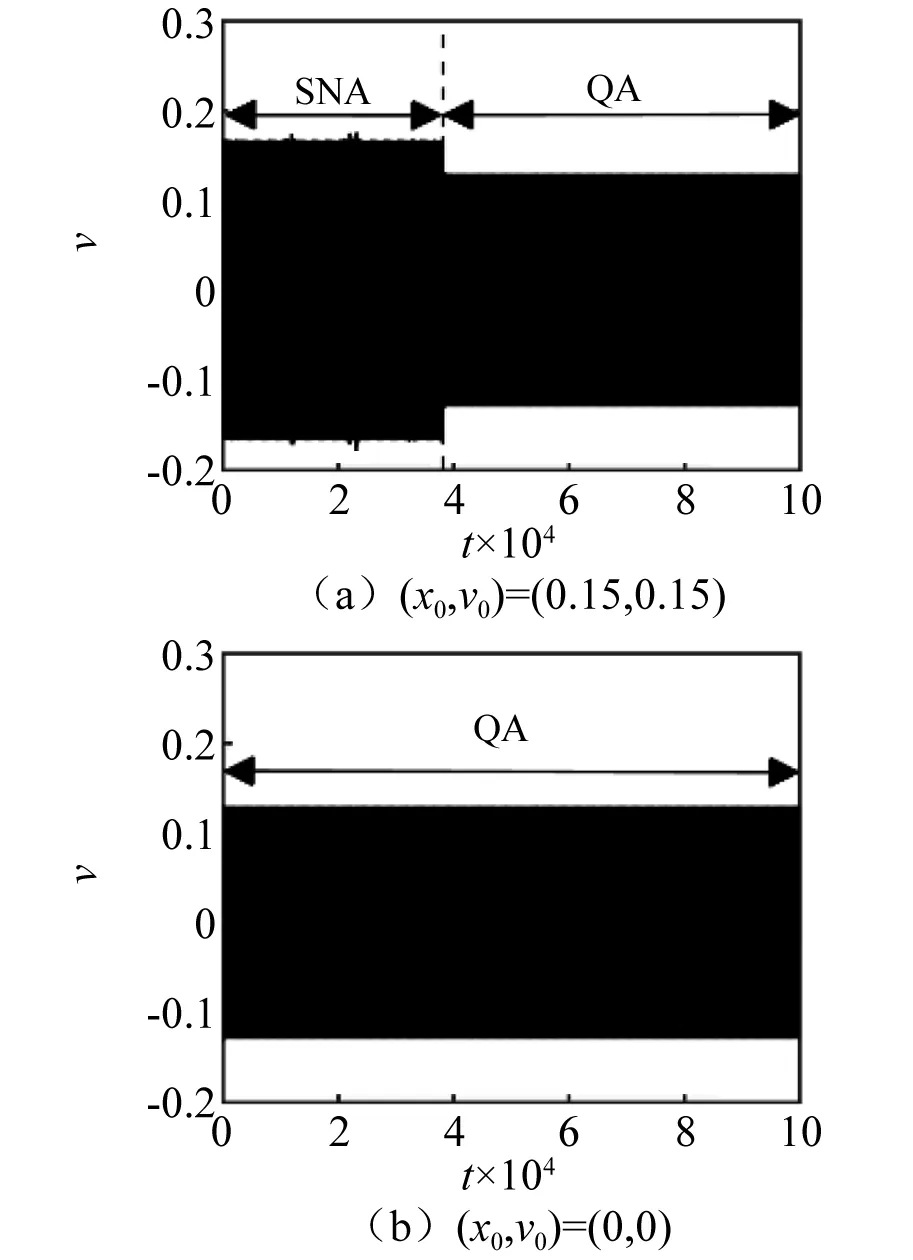
圖23 α=0.608 27狀態變量v的時間序列Fig.23 Time series of the state variable v when α=0.608 27

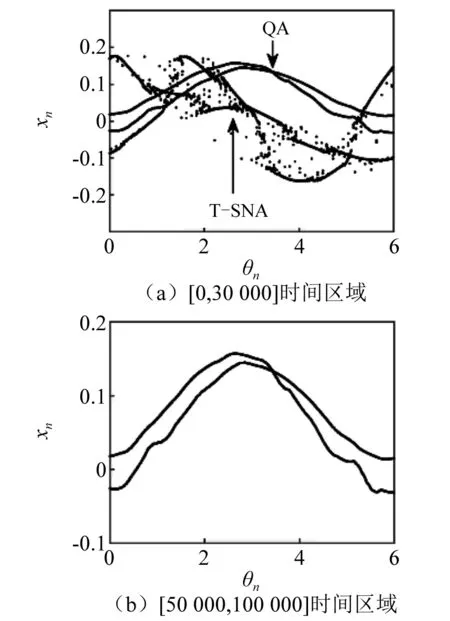
圖24 α=0.608 27時(θn,xn)平面上相圖Fig.24 For α=0.608 27, phase diagrams in (θn,xn)

當α=0.599時，系統由暫態SNA演化為暫態混沌，如圖25(a)所示，同樣地，圖25(b)為初始條件為(0,0)時，系統狀態變量v的時間序列。圖26(a)展示了系統在[0,30 000]時間區域內SNA與暫態混沌的共存情況。圖26(b)為系統在[50 000,100 000]時間區域內的相圖，此時系統暫態混沌吸引子已轉變為SNA。通過圖27系統最大Lyapunov指數發現，隨著時間不斷演化，最大Lyapunov指數由正值進入負值，這也表明了系統的暫態混沌發生轉移。

圖25 α=0.599狀態變量v的時間序列Fig.25 Time series of the state variable v when α=0.599

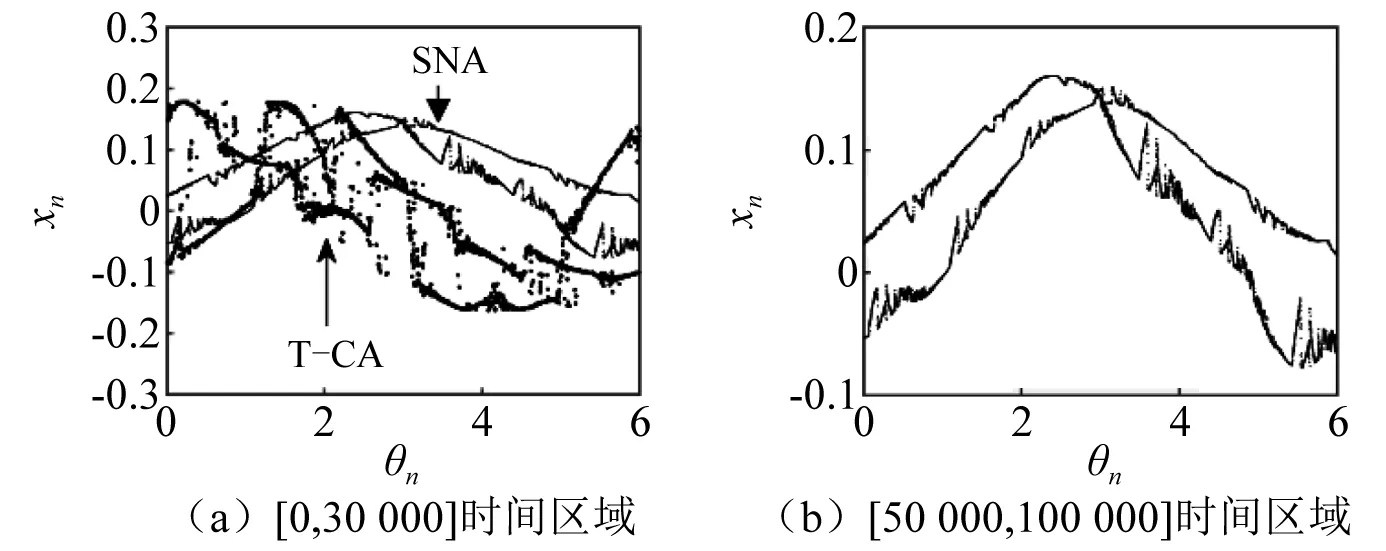
圖26 α=0.599時(θn,xn)平面上相圖Fig.26 For α=0.599, phase diagrams in (θn,xn)

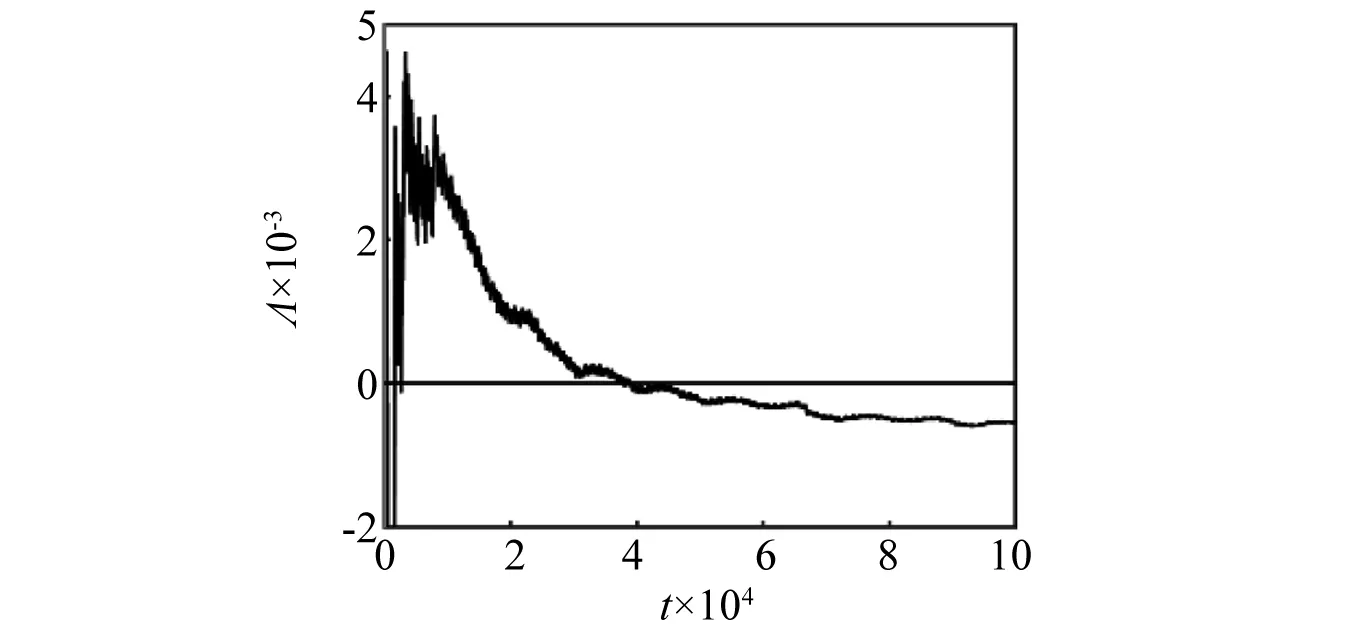
圖27 α=0.599， (x0,v0)=(0.15,0.15)時最大Lyapunov指數譜Fig.27 For α=0.599, (x0,v0)=(0.15,0.15) top Lyapunov exponent

而當α最終減小到0.593時，系統此時僅存混沌運動，如圖28所示，其對應的最大Lyapunov指數為0.004。

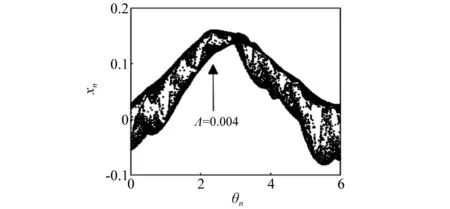
圖28 α=0.593時(θn,xn)平面上相圖Fig.28 For α=0.593, phase diagrams in (θn,xn)

6 結 論

奇異非混沌動力學的研究已經開展了三十多年，目前大多數的研究主要針對于不同領域的離散或光滑系統。本文以一類雙頻激勵的具有懸臂結構的碰撞振動系統為研究對象，建立了系統的運動微分方程。利用相敏感函數、奇異連續譜、有理數頻率逼近、狀態變量的傅里葉變換的部分和在復平面上的路徑、最大Lyapunov指數等工具，揭示了懸臂碰撞振動系統豐富而又復雜的奇異非混沌動力學及其多穩態現象。研究結果表明：

(1) 通常擬周期運動通過無限次的倍化可直接通向混沌。而本系統1T環面經過一次倍化而變成2T環面后，擬周期吸引子便產生扭曲和褶皺，從而導致倍化終止。隨著參數變化，擬周期吸引子首先演化為SNA，最后通向混沌。

(2) 在某些參數區間，系統存在通向SNAs的不同路徑，即分形路徑和陣發路徑。分形路徑的顯著特征是擬周期吸引子產生褶皺狀，這也可視為SNAs出現的前兆，而陣發路徑的特征是原擬周期吸引子附近出現散亂無序的離散點，直到演變為SNAs。

(3) 系統存在暫態及穩態SNAs與擬周期吸引子的共存、穩態SNAs與混沌吸引子的共存情況，首先出現的SNA是由陣發路徑而產生，且通過數值計算發現其共存區間較短。當穩態SNA轉變為暫態SNA后，另一個擬周期吸引子也逐漸開始向SNA演化。當后面的擬周期吸引子演變為SNA時，系統暫態SNA也演化為暫態混沌吸引子，此時系統SNA與暫態混沌吸引子發生共存。最終，系統暫態混沌消失，SNA轉遷為穩定的混沌吸引子。

本文的研究方法和結果可為非光滑連續系統中的奇異非混沌動力學理論研究提供思路，同時也可為工程中含懸臂結構的相關碰撞裝置或構件的設計和優化提供理論支持。