基于增秩Kalman濾波的移動車輛荷載在線識別

張超東， 黎劍安， 張 浩

(1. 深圳大學 土木與交通工程學院 城市智慧交通與安全運維研究院，廣東 深圳 518060；2. 石家莊鐵道大學 省部共建交通工程結構力學行為與系統安全國家重點實驗室，石家莊 050043)

車輛荷載是在役公路橋梁所承受的主要活荷載之一。移動車輛通過橋梁時，橋梁受到車輛激勵產生振動，反過來也對車輛產生激勵，兩者相互耦合相互影響，被稱為車橋耦合振動。近年來，由于組合結構、預應力等新結構形式及高強鋼結構和高性能混凝土等新材料的應用，我國公路橋梁的跨度不斷增大，向更輕、更柔性的方向發展。加之車輛行車速度提高、載質量增加，公路橋梁因車橋耦合作用而產生的車輛荷載放大效應也不斷凸顯。在路面粗糙度較差的情況下，車橋耦合作用下的車輛荷載可能是車體自身質量的2～4倍[1]，獲取車橋耦合荷載對于車輛超載預警和橋梁結構狀態評估具有重要的意義。由于測量手段的限制、測量環境的惡劣以及結構的復雜性等諸多因素，車輛與橋梁之間的相互作用力通常難以直接測量[2]，識別橋梁受到的車輛荷載日益成為橋梁結構健康監測和安全評估的關鍵。

目前對車輛荷載進行監控的主要手段是橋梁動態稱重系統(bridge weigh-in-motion，B-WIM)，其利用壓電線圈或橋梁動力響應反演橋面移動車輛等效靜荷載。B-WIM已經在實體橋梁上得到了較多應用，但仍然存在一些不足。B-WIM通常基于Moses[3]靜態算法，其假設移動荷載將導致橋梁與荷載大小成比例的彎曲，沒有考慮車輛與橋梁之間動態耦合效應，因此無法識別移動車輛荷載。

近年來大量考慮橋梁動態特性的移動荷載識別(moving force identification，MFI)方法被提出。此類方法以橋梁上動力響應(加速度、彎矩等)作為已知輸入，利用理論分析或有限元計算得到移動荷載與橋梁動力響應的關系，進而將移動荷載識別問題轉化為最小二乘求解問題。目前方法主要有兩類：時域法[4]和頻域法[5]。時域法基于運動方程，通過荷載與響應的卷積積分來確定移動荷載。頻域法在頻域中求解移動荷載，然后通過傅里葉逆變換確定荷載時程。與頻域法相比，時域法擁有更高的精度，適用范圍也更廣。基于這兩類方法，近年來很多移動荷載識別的新方法被提出來了。Liu等[6]基于混合數值方法，應用格林函數和Heaviside階躍激勵的響應函數來確定復合材料表面的線荷載。Chan等[7]基于歐拉梁的運動方程，結合模態疊加法求解移動荷載。

作為一個典型的振動第二逆問題，移動荷載識別是一個典型的不適定性問題，即測量響應含有微小噪音可能引起識別的移動荷載中出現不可接受的偏差。目前該研究的熱點在于克服反問題的不適定性，基函數法[8]、正則化方法[9-10]等是最為常用的方法。潘楚東等[11]提出了考慮初始條件的荷載識別方法，該方法利用冗余字典和稀疏正則化方法求解荷載并得到了不錯的精度。Asnachinda等[12]基于有限元建模，提出了將更新靜態分量的方法應用到連續橋上識別移動荷載。Zhu等[13]提出了基于狀態空間法和正則化方法求解移動荷載的方法，但精度容易受到傳感器位置的影響。Qiao等[14]利用三次B樣條函數和小波分析提出了一種拓展基函數荷載識別算法。Busby等[15]將基于L曲線的正則化方法首次應用在移動荷載識別，開拓了采用正則化方法解決移動荷載識別的研究方向。Zhong等[16]提出了基于L1范數的稀疏正則化的方法，利用試驗驗證了該方法并取得了不錯的精度。

以上所述的移動車輛荷載識別方法仍存在三方面的不足：①基于最小二乘框架下的移動荷載識別通常涉及到系統矩陣偽逆操作，不適定性問題突出，即荷載識別結果很容易受到噪聲的擾動而導致結果誤差很大甚至發散；②此類方法需使用批量響應序列識別車輛荷載形成超靜定方程組，因而無法在線識別荷載；③目前的移動車輛荷載識別方法一般僅建立橋梁結構模型，采用假定車輛荷載動態作用力，未充分考慮車橋耦合振動效應，也無法討論路面不平度對荷載識別的影響。

為充分考慮車橋耦合作用下的移動荷載識別，需建立車橋耦合振動方程。車橋耦合模型由車輛荷載模型和橋梁模型組成，目前的文獻中已有多種橋梁-車輛耦合模型。鑒于三維橋梁模型的復雜性，目前移動荷載研究采用的橋梁模型仍以二維的簡支梁橋或連續梁橋模型為主。車輛模型主要包括移動恒載模型、移動簡諧荷載模型[17]、移動質量塊模型[18]、彈簧質量模型[19]、1/4車輛模型[20]、半車模型[21]以及三維車輛模型[22]。早期的荷載模型相對較簡單，并不能較好地反映車輛與橋梁之間相互作用的真實情況。彈簧質量模型、1/4車輛模型和半車模型則能相對較好地反映車輛與橋梁之間的動態效應而且計算量也相對較小；三維車輛模型雖能更完整地反映車輛與橋梁之間的運動狀態，但建模過程相對復雜且計算成本較大。

本文基于車橋耦合系統模型，提出基于增秩Kalman濾波的移動車輛荷載在線識別算法。首先建立能考慮路面不平整度的車橋耦合振動方程，計算車輛和橋梁的動力響應以及車橋相互作用力，即車輛荷載。其次，建立橋梁結構的狀態空間方程，將移動車輛荷載與狀態向量聯立構成增秩狀態向量。基于增秩Kalman濾波算法，利用少量測點處的橋梁振動響應，實時遞歸迭代獲得增秩狀態向量的無偏最小方差估計，實現車輛荷載實時識別。相較于現有的車輛荷載識別算法，本文所提出的基于增秩Kalman濾波算算法具有突出的優勢：首先，利用增秩Kalman算法獲得移動車輛荷載最佳估計，避免了直接求解反問題帶來的不適定性，因此荷載識別精度較高，且結果相對較穩定。其次，增秩Kalman濾波算法能融合多種響應測量值(如加速度和應變)并聯合模型預測給出增秩狀態向量的最優估計，可同時考慮觀測噪聲和系統噪聲，因此對測量噪音和系統誤差有較強的魯棒性。

1 車橋耦合模型

本文采用的車橋耦合系統模型示意圖，如圖1所示，其中橋梁模型選用歐拉-伯努利簡支梁橋，車輛模型選用擁有一個自由度的彈簧質量模型。圖1中：m1和m2分別為車輪質量和彈簧上物體質量；c和k分別為懸掛系統的阻尼系數和剛度系數；z為彈簧質量的豎向位移；ρ為橋梁每延米的質量；EI為橋梁的抗彎剛度；L為橋梁的長度；v為車輛的移動速度；g為重力加速度；橋面在x處的豎向撓度為yb(x,t)，其中x=vt。

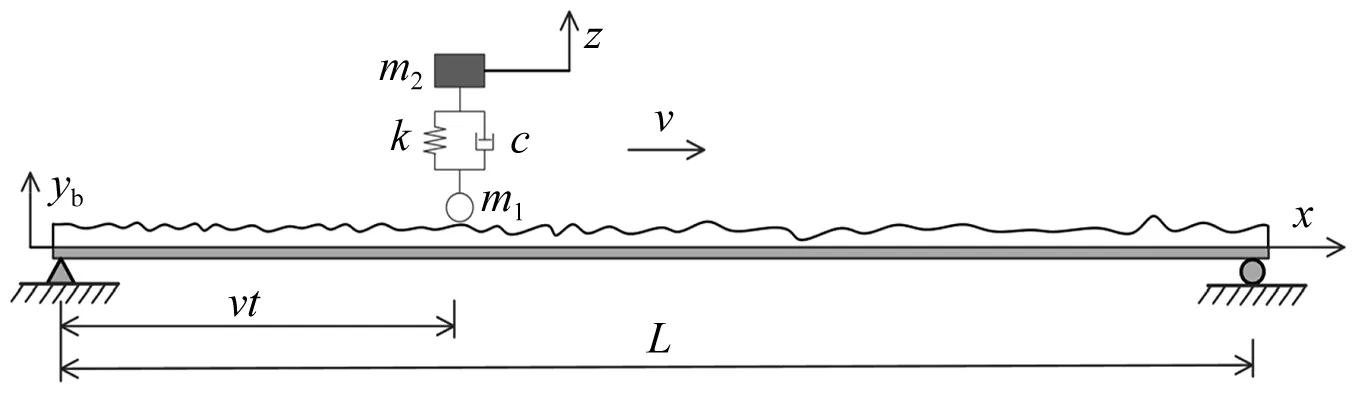
圖1 車橋耦合系統Fig.1 Vehicle bridge interaction system

1.1 路面不平度模擬

路面的粗糙度是影響動態效應的重要因素，在ISO 8608：2016標準[23]中，路面不平度被劃分為從A級(最好)～H級(最差)8個等級。鑒于橋梁表面的粗糙度相對較好，本文的路面不平度分析僅采用該標準中的前5個等級。路面不平度的表達式為

(1)

(2)

式中：r(x)為路面不平度信號；N為路面離散點的數量；Gk為路面不平度的功率譜密度函數；nk為空間頻率；Δn為空間頻率的間距，Δn=(nu-nl)/N，一般地，nl=0.011 m-1，nu=2.83 m-1；n0為參考空間頻率，一般取0.1 cycles/m；x為橋梁的橫坐標；φk為滿足(0,2π)的均勻分布數列；G0的取值需要參考路面不平度的等級。

1.2 橋梁運動方程

建立圖1中簡支梁的有限元模型，其運動方程為

(3)

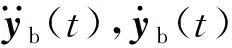
H(t)=[0…Ψ(x0,t) …0]T

(4)

在矩陣H(t)中，移動荷載所作用的單元用形函數Ψ(x0,t)表示，其他單元全用零矩陣代替，從而表示出移動荷載的位置。由于移動車輛的位置在不斷變化，所以每一個時間步內都需要對矩陣H(t)進行更新。fint(t)為作用在橋梁上的移動車輛荷載[25]，其表達式如式(5)所示

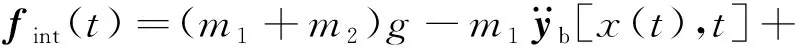
(5)

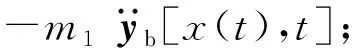
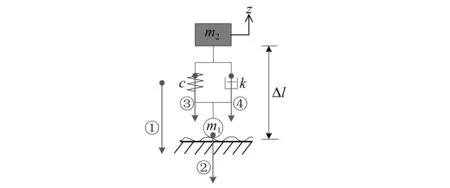
圖2 車輛荷載力學模型示意圖Fig.2 Schematic diagram of vehicle load mechanics model

yb[x(t),t]=HT(t)yb(t)

(6)

模態疊加技術可大大提高計算復雜系統的效率，橋梁的位移矩陣用模態疊加法可表示為

yb(t)=Φ(t)q(t)

(7)

式中：Φ(t)為橋梁的振型矩陣；q(t)為模態坐標向量。

1.3 車輛運動方程

圖1中的車輛模型用運動方程可表示為

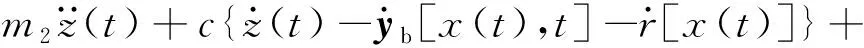
(8)

該車輛模型只有一個自由度，故車輛模型不采用模態疊加法。

1.4 車橋耦合振動方程

Zhu等[27]指出車橋耦合方程的解法有兩種：一種是在兩個的子系統中分別求解車輛方程和橋梁方程；另一種方法是將車輛方程和橋梁方程聯立求解。本文采用第2種方法求解，聯立式(3)和式(8)得到車橋系統的耦合振動方程如式(9)所示

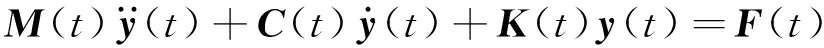
(9)

其中，

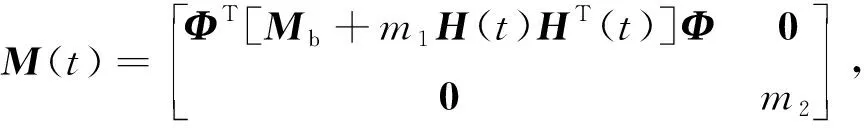
利用Newmark-β逐步積分法或者離散狀態空間法對式(9)迭代可以求解車橋耦合系統的動態響應，進而可將部分響應作為觀測量用于識別移動車輛荷載。

根據式(5)可以計算出車輛荷載的真實值，其可作為標準與識別到的車輛荷載進行比較，以評價識別結果的準確性。本文接下來的第2章將進一步闡述基于AKF算法的移動荷載識別原理。

2 基于AKF的移動車輛荷載識別

2.1 橋梁結構的狀態空間方程

根據式(3)建立橋梁結構的狀態空間方程為

(10)

其中，

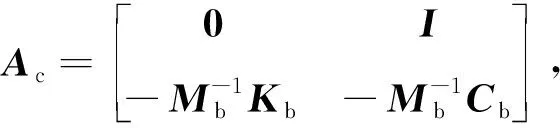
式中，I為單位矩陣。

將式(10)離散化，并施加系統的過程噪聲，過程噪聲用ωk表示

Xk+1=AdXk+Bdpk+ωk

(11)

其中，

建立系統的測量方程，并施加測量噪聲，測量方程的形式為

dk=CdXk+Ddpk+ξk

(12)

式中，Cd和Dd分別為狀態空間的觀測矩陣和前饋矩陣，可由式(10)構建，用以輸出所需的動態響應dk。ξk為觀測噪聲。橋梁狀態空間方程詳細的建立過程可參考文獻[28]。

2.2 移動車輛荷載識別

利用式(12)求解移動荷載pk的過程中，由于觀測值dk并不包含所有節點的動態響應，只能通過部分的觀測值求解移動荷載，所以直接求解是困難的。并且由于觀測值含有觀測噪聲以及系統模型的建立含有一定的偏差，求解結果容易因為輕微的干擾而產生很大的誤差。AKF利用最優估計的方法求解反問題，求解過程結合觀測噪聲和模型噪聲，其結果不容易因為數據的波動而產生較大誤差，適合用于求解移動荷載。

假設荷載pk在第k個時間步的增量為ηk，則荷載pk的遞推關系式可表示為

pk+1=pk+ηk

(13)

聯立式(11)和式(12)，并將pk作為狀態變量增廣到狀態向量Xk中，得到車橋系統的增秩狀態空間方程為

(14)

dk=CaXk+ξk

(15)

其中，

利用AKF算法求解車輛荷載分為兩個部分[29]：

(1) 預測部分

(16)

(17)

(2) 更新部分

(18)

(19)

(20)

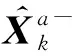
在式(17)和式(18)中

(21)

式中： E 為取數學期望；T為ζk的協方差矩陣，表示系統模型的誤差；R為ξk的協方差矩陣，表示觀測值的誤差。AKF算法通過聯合T和R給出狀態向量的最優估計：T越小表明模型誤差越小，Kalman增益就越信任預估計；反之則越信任觀測值。

(22)

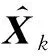
圖3 基于AKF的車橋耦合荷載識別流程圖Fig.3 Flow chart of vehicle-bridge interaction load identification based on AKF

3 車橋耦合系統數值模擬

為驗證本文所提方法的可行性，以圖1所示的簡支梁-彈簧質量組成的車橋耦合模型為例進行數值模擬。車輛的參數如下：m1=3 000 kg，m2=31 700 kg，c=8.6×104N·s/m，k=9.12×106N/m。橋梁的參數如下：L=40 m，EI=2.3×1010N·m2，每延米的質量ρ=5×103kg/m，所有模態的阻尼比均為2%。

將簡支梁劃分為40個等長度梁單元，建立該橋梁的有限元模型，每個節點僅考慮豎向位移和轉角，忽略軸向位移。將高斯白噪聲作為測量噪聲加入到純凈的仿真響應中，用以模仿包含噪聲的測量數據，施加噪聲的公式為

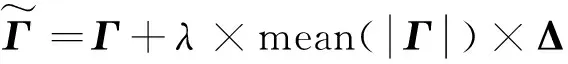
(23)

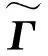
為評價車輛荷載的識別精度，將識別誤差[30]定義為

(24)

式中：ε為識別誤差；Ωtrue為橋梁受到的真實荷載，由式(5)計算得出，用作評定識別荷載的標準；Ωid為識別荷載，由AKF算法利用橋梁振動識別得出； ‖·‖2為目標數列的L2范數。

如表1所示，C1～C5為本文討論到的傳感器組合，數量依次遞增，傳感器的安裝位置可參考圖4。在圖4中，位移傳感器和加速度傳感器分別安裝在橋梁1/4跨、1/2跨和3/4跨處，其中D代表位移傳感器；A表示加速度傳感器。

表1 傳感器組合Tab.1 Sensor combination

圖4 傳感器布置示意圖Fig.4 Schematic diagram of sensor layout

下文對影響車輛荷載識別精度的各項因素進行了探討，在未經申明的情況下，默認車速取30 m/s，噪聲取5%，路面不平度取A級，采樣頻率取1 000 Hz，傳感器組合取C5組合。

3.1 路面不平度的影響

路面不平度是影響車輛荷載大小的重要指標，也會影響到接觸力的識別精度。本文取ISO標準路面不平度的前5個等級(即A～E級)作為路面不平度討論因素。

圖5為各等級路面不平度下，車輛荷載與靜載(車體自質量)的比值的箱線圖，其中“S”表示完全光滑的路面類型。從圖5中可以看出，在各等級的路面不平度下，荷載比值的中位數基本上維持在1處，這是因為車輛是圍繞靜載波動的，中位數也就與靜載相接近。隨著路況變差，路面不平度增大，移動車輛荷載的分布范圍變大，波動更為劇烈。表明移動車輛動態效應越顯著，車輛與橋梁之間的車輛荷載就越大。而箱線圖中的最大值則更直觀地表現了車輛荷載與靜載的關系，如E級路面下，車輛荷載的最大值達到了靜載的4倍，這表明橋梁受到的車輛荷載是不容忽視的。可以說，路面不平度越差，橋梁受到的車輛荷載就越大，進而使橋梁更容易受到損傷,這也體現了識別車橋耦合車輛荷載對于橋梁健康監測的重要性。

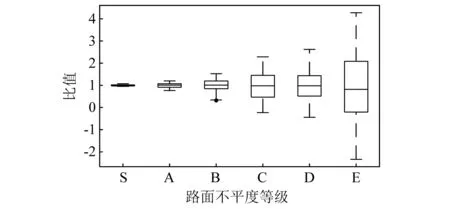
圖5 各等級路面下車輛荷載與靜載比值箱線圖Fig.5 Box plot of the ratio of dynamic load to vehicle weight for each road surface level

圖6為A級路面不平度條件下車輛荷載的識別結果，識別誤差為1.32%。圖7為E級路面不平度條件下車輛荷載的識別結果，識別誤差為5.26%。相比于圖6，圖7的誤差雖然有所增加，但仍然處于較低的水平。值得注意的是，圖7中的車輛荷載明顯大于圖6中的車輛荷載，這進一步說明路面粗糙度會明顯影響到車輛荷載的大小。

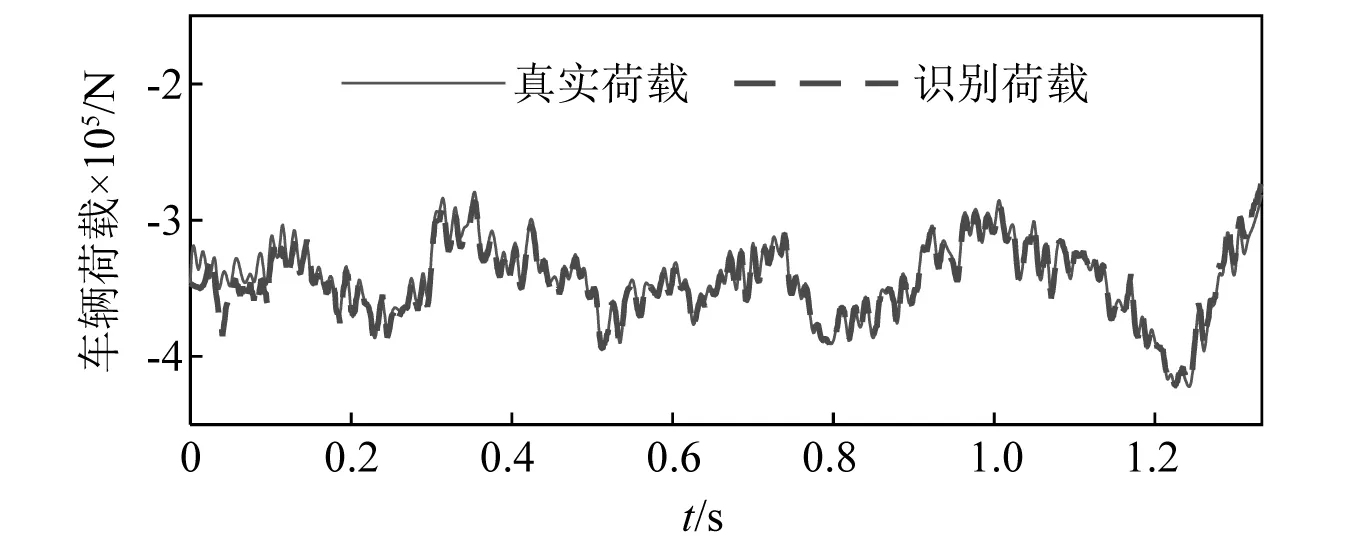
圖6 A級路面不平度的車輛荷載識別圖Fig.6 Identification diagram of vehicle load for A level pavement

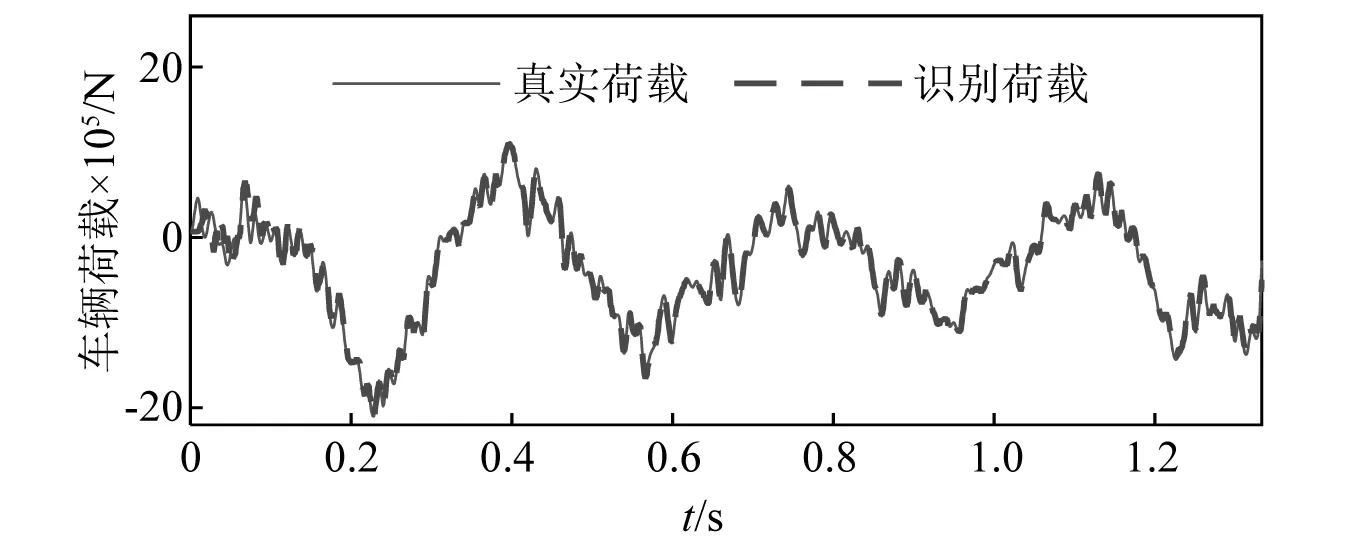
圖7 E級路面不平度的車輛荷載識別結果Fig.7 Identification diagram of vehicle load for E level pavement

圖8為不同路面粗糙度下車輛荷載的識別誤差曲線，隨著路面粗糙度變差，車輛荷載的識別誤差也越來越大，但是增量并不明顯，在最不利的路面下誤差僅有5.26%，這樣的增幅是可接受的。由于橋梁表面的不平整度一般不會太差，故無需考慮E級路面之后的荷載識別情況了。

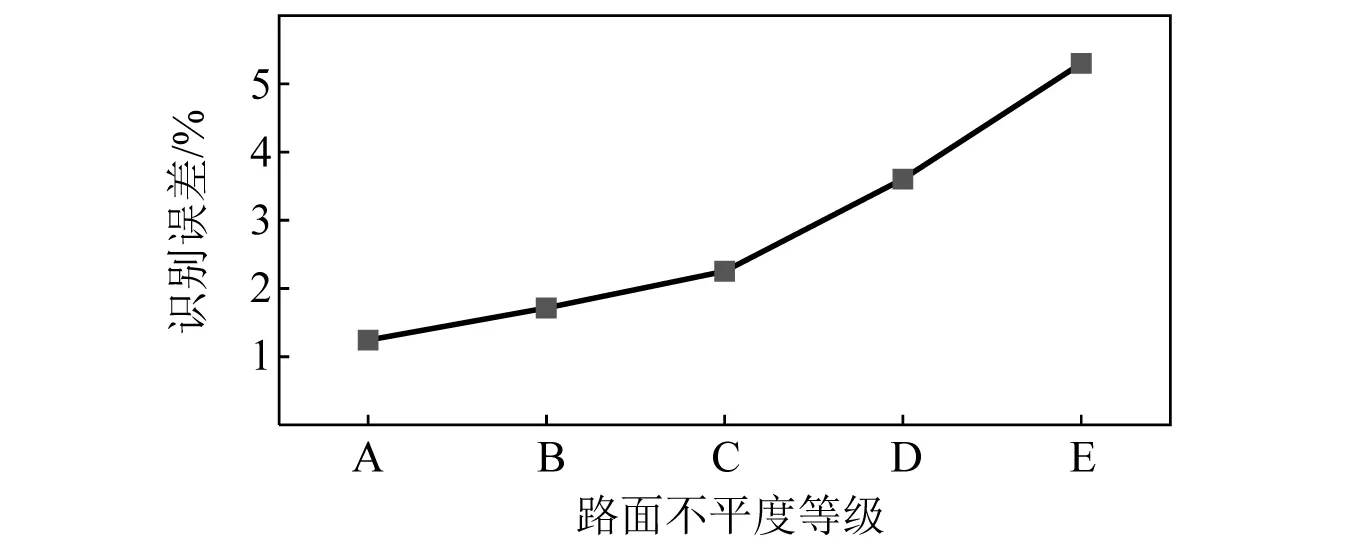
圖8 不同路面不平度下車輛荷載的識別誤差Fig.8 Identification error of vehicle load under different road roughness

3.2 車速的影響

圖9展示了車輛在A級不平度的路面上，車速處于10～100 m/s時識別誤差的變化曲線。可以看出，車速的變化對識別精度的干擾很小，誤差值雖然呈緩慢上升的趨勢，但上升幅度非常小，即使在100 m/s的車速下，識別誤差依然能保持在3%以內。需要說明的是普通汽車的速度一般在40 m/s以下，此時誤差值在2%以內，這說明所提方法的識別結果對車速不敏感。

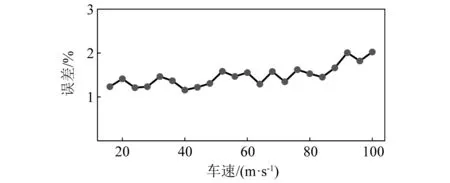
圖9 不同車速下車輛荷載識別誤差Fig.9 Identification error of vehicle load at different speeds

3.3 噪聲的影響

圖10～圖12分別展示了噪聲在2%，15%和40%時的荷載識別結果，誤差分別是1.12%，1.78%和3.29%。從圖中可以看出，三種情況下荷載識別精度都相對較高。如圖12所示，即使是在40%噪聲的干擾下，識別荷載與真實荷載依然達到了相對較高的重疊程度，但在橋梁兩端處，荷載的識別精度較差。這一現象在文獻[31]中也有見到。

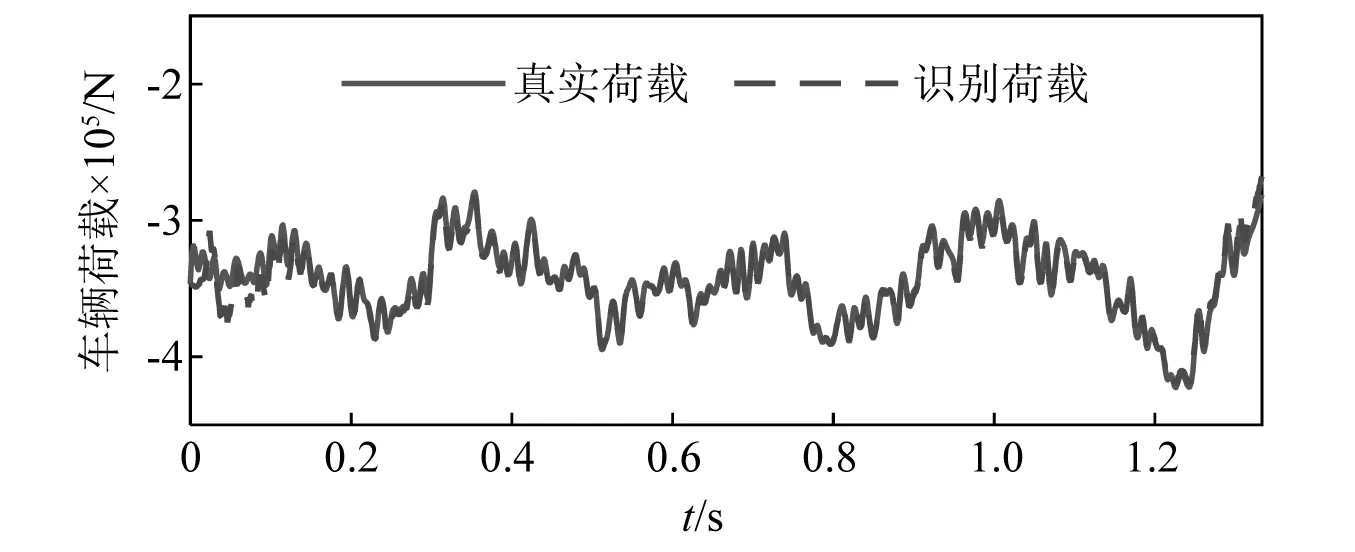
圖10 噪聲為2%時車輛荷載識別誤差Fig.10 Identification error of vehicle load at (2% noise)

圖11 噪聲為15%時車輛荷載識別誤差Fig.11 Identification error of vehicle load at (15% noise)

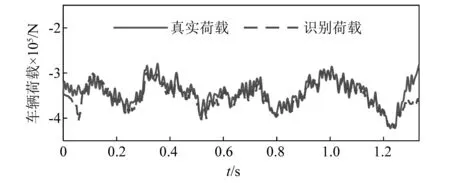
圖12 噪聲為40%時車輛荷載識別誤差Fig.12 Identification error of vehicle load (40% noise)

需要指出的是：多數文獻的數值算例中，引入的噪聲比例不會超過15%。本文最多考慮了40%噪聲，強大的處理噪聲的能力是所提方法區別于其他現有方法的優勢。

圖13展示了噪聲從2%～40%的誤差曲線，隨著噪聲的增加，誤差曲線呈緩慢上升的趨勢。即使是在40%的噪聲條件下，識別誤差依然能保持在3%左右，可以說本文提出的方法具有強大的抵抗噪聲干擾的能力。這是因為AKF算法聯合系統估計誤差和觀測誤差，將最優估計的理論誤差降到最小，以此達到過濾噪聲的目的。

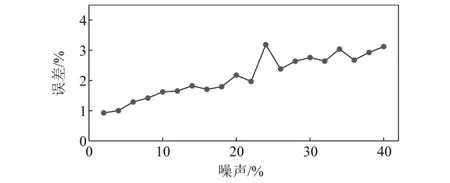
圖13 不同噪聲下的車輛荷載識別誤差Fig.13 Identification error of vehicle load under different noises

3.4 傳感器配置的影響

很多論文都將傳感器的數量納入影響荷載識別精度的指標，傳感器數量越多，采集到的數據就越完善，計算的結果也就越接近真實值。但是傳感器是昂貴的，其數量越多經濟成本就越大，所以用盡量少的傳感器進行結構健康監測日益成為學者們研究的方向。本文討論了表1所示的5組傳感器組合、最多6個傳感器對荷載識別精度的影響。

圖14展示了C1組合下，車輛荷載的識別結果，可以看出誤差主要集中在橋梁兩端，而荷載處于中間時誤差較小。圖15展示了5種組合傳感器組合的識別誤差。傳感器數量最少的C1組合識別誤差是最大的，誤差值為5.93%，依然處于比較小的誤差水平。圖15中各工況下的誤差值均處于7%以內，這說明了本文所提的方法能用較少的傳感器完成車輛荷載的識別，但采用的傳感器數量越少，荷載識別誤差也越大。

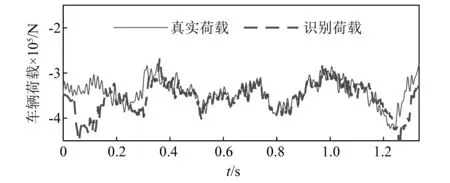
圖14 C1組合下車輛荷載識別結果Fig.14 Identification result of vehicle load (case: C1)

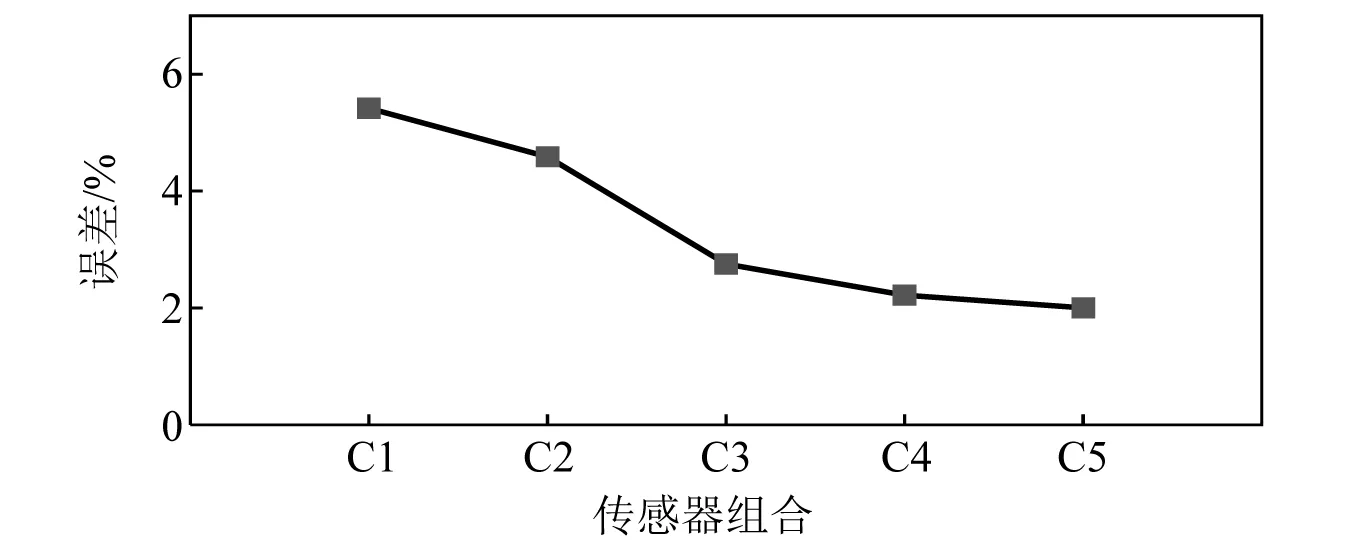
圖15 各傳感器組合下車輛荷載識別誤差Fig.15 Identification error of vehicle load under each sensor case

3.5 采樣頻率的影響

采樣頻率是影響荷載識別精度的重要指標，當采樣頻率只有100 Hz的時候，所提方法在默認工況下識別車輛荷載的誤差在8%左右，依然處于相對較低的誤差水平。如圖16所示，提高采樣頻率能明顯改善荷載識別精度，當采樣頻率達到1 000 Hz的時候，識別精度的提升則顯得相對微弱了。這說明過低的采樣頻率會影響到所提方法的準確性，但采樣頻率達到200 Hz或以上時，荷載識別精度相對可靠。

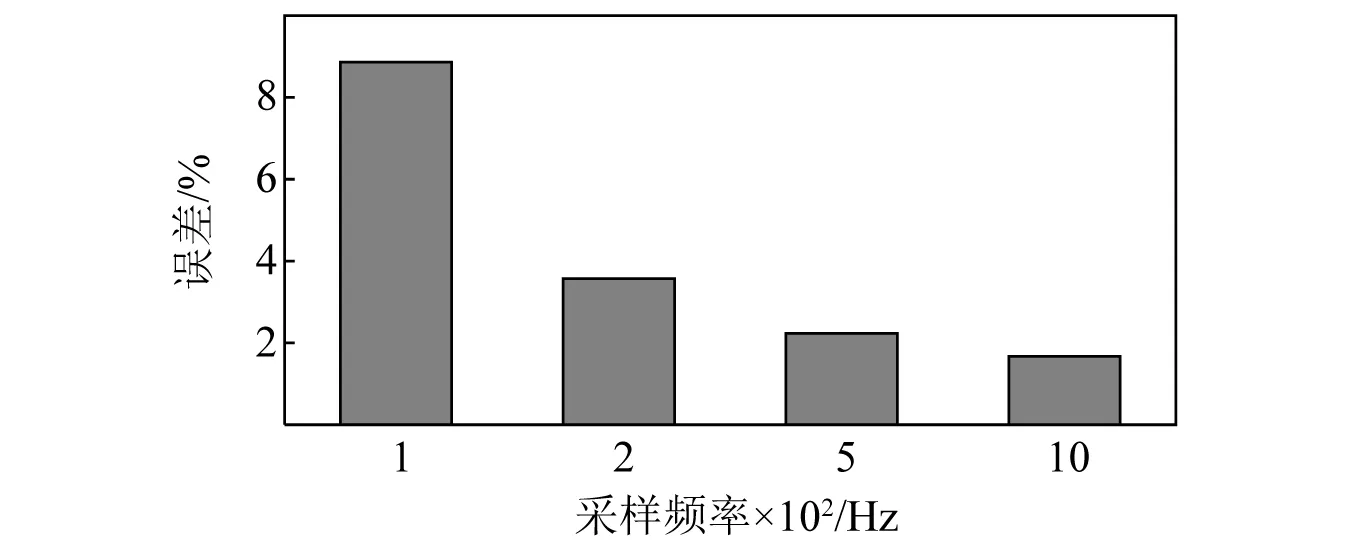
圖16 各采樣頻率的誤差對比Fig.16 Error comparison of each sampling frequency

3.6 與現有方法對比

基于車橋耦合的移動車輛荷載識別的相關文獻比較有限，本節將本文所提的方法與模型相近的文獻[32]相對比。文獻所提的方法(加權L1范數正則化方法，W-L1R)精度較高，具有一定的參考性。

兩者的仿真模型的主要區別在于：①Pan等采用的是模擬的帶有沖擊效果的簡諧荷載，而本文采用的是基于彈簧質量模型的車橋耦合荷載，更能反映車輛與橋梁之間的實際作用；②Pan等沒有考慮橋面的不平順，本文考慮了橋面不平順且發現橋面不平順對荷載的識別精度是有影響的。

表2為參考Pan等研究中的各方法識別荷載的誤差對比結果。統一用橋梁的跨中加速度響應和1/4跨處彎矩響應來識別移動車輛荷載。由表2可知， W-L1R方法識別車輛荷載精度稍好于本文做提的基于 AKF的方法；而AKF的方法明顯好于L1范數正則化和Tikhonov正則化移動荷載識別方法。

表2 各方法的識別誤差對比Tab.2 Error comparison of methods %

表3為不同測點下，本文所提方法(AKF)和Pan等所提方法(W-L1R)的誤差對比，其中1/4m表示1/4跨彎矩測點，1/2a表示跨中加速度測點。當測點僅選用1/4m的時候，W-L1R方法識別車輛荷載精度稍好于基于AKF的方法，而當測點選用1/2a的時候，基于AKF的方法識別車輛荷載精度稍好于W-L1R方法。

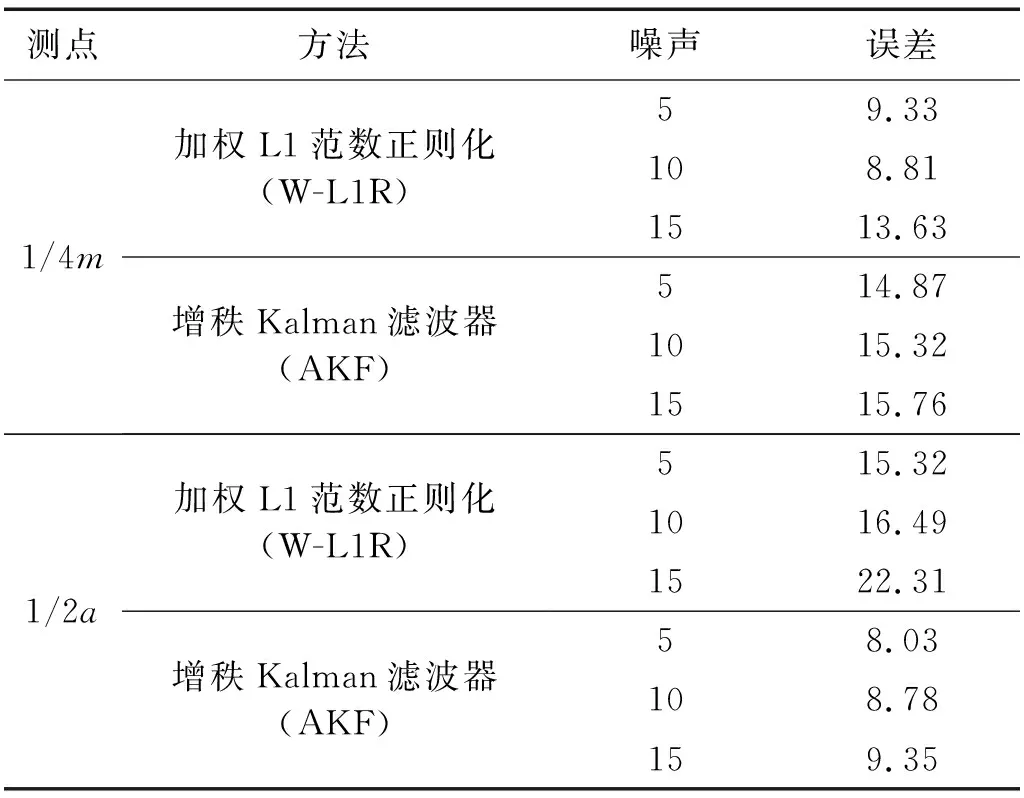
表3 不同測點的識別誤差對比Tab.3 Error comparison of different measurements %

綜上所述，傳感器的種類和位置對不同方法識別移動車輛荷載影響不同。僅從誤差上看，本文所提的基于AKF算法識別移動車輛荷載與W-L1R識別精度相當，都優于L1范數正則化和Tikhonov正則化車輛荷載識別算法。但是需要指出的是，基于本文所用的荷載模型考慮了橋面不平整度，同時所提的算法是一種遞歸算法可以實現車輛荷載在線識別。

4 結 論

為驗所提方法的可行性和準確性，本文基于由簡支梁橋-彈簧質量模型構成的車橋耦合系統，詳細討論了路面粗糙程度、車速、噪聲、傳感器配置和采樣頻率對車輛荷載識別誤差的影響，列出了詳細的工況并與現有方法進行對比，得出以下結論：

(1) 基于AKF的移動荷載識別方法能利用較少數量的傳感器獲得的橋梁動態響應有效地識別移動車輛與橋梁之間的接觸力。

(2) 所提方法對車速和噪聲不敏感。隨著噪聲的增加，所提方法的識別誤差小幅增加，當噪聲為40%時，識別誤差僅為3%左右。所提方法受車速影響也不明顯，隨著車速的增加，所提方法的識別誤差緩慢增加，最高僅為2%左右。

(3) 傳感器的配置和采樣頻率是重要的影響因素。當所用到的傳感器數量過少或者采樣頻率太低時，所提方法的識別精度較低。

(4) 較差的路面不平度不但會明顯增大車橋相互作用力，而且會降低基于AKF的車輛荷載識別的精度。但數值結果表明，在路面狀況較差的情況下，所提的方法識別車輛荷載仍較小(E級路面荷載識別誤差為5.26%)。

(5) 所提的方法采用逐步迭代的方法識別車輛荷載，無需提前獲取結構的全時程響應，為車輛荷載的實時識別提供新的方法。

(6) 仿真結果顯示，在荷載進入橋梁時，荷載未能得到良好的識別效果，這是該方法較為明顯的不足，也是我們接下來的研究方向。