基于EMB的純電動汽車制動能量回收優化控制策略研究*

常九健，張煜帆

（1.合肥工業大學智能制造技術研究院，合肥 230000；2.合肥工業大學汽車與交通工程學院，合肥 230000）

前言

隨著科技進步和社會發展，汽車保有量逐年遞增，石油、煤炭、天然氣等不可再生能源的需求急劇增長，帶來了能源消耗和環境污染等問題。純電動汽車以其結構簡單、噪聲小、零排放的特點備受世界關注，另外電動汽車可以進行制動能量回收，從而提高整車能量利用率、彌補續航里程不足問題。作為新能源汽車研究的新方向，電子機械制動（EMB）系統反應靈敏，制動效能高，結構簡單，易于和其他系統進行綜合控制，且可大幅提升整車的能量利用率，近年來受到了廣泛關注。

汽車的再生制動控制策略也不斷發展，有固定比例的分配策略、神經網絡控制策略和遺傳算法控制策略等。但是對基于EMB 系統的制動能量回收控制的研究還很少。本文中提出了一種在電子機械制動的基礎上，采用PSO 算法優化模糊控制的制動能量回收控制策略，以最大化回收能量為目標，對模糊控制進行優化。再通過Simulink 和AVL Cruise 聯合仿真進行驗證。結果表明，所采用的策略增加了回收的制動能量。

1 電子機械制動系統

1.1 電子機械制動系統的工作原理

EMB 系統由EMB 控制器和EMB 執行器兩部分組成。其中，EMB 執行器包括驅動電機、減速增轉矩裝置和運動轉換機構3 個部分；而EMB 控制器作用是控制電機的轉動，運動轉換機構作用是將旋轉運動轉變為平移運動，使經過減速增轉矩裝置的力矩轉換成推動制動盤墊片的壓緊制動力，從而達到制動的效果。

1.2 電子機械制動系統模型

EMB 系統采用壓力-轉速-電流三閉環控制。內環是電流控制環，輸入為轉速控制環所輸出的目標電流與實際電流的差值；外環為壓緊力控制環，輸入為目標制動壓緊力與反饋制動壓緊力的差值，如圖1所示。

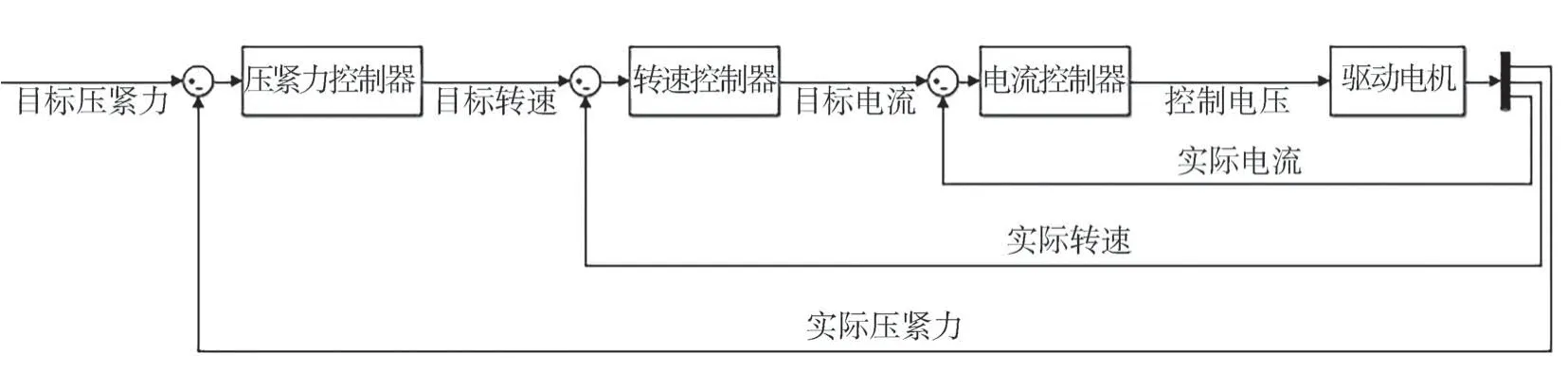
圖1 壓力-轉速-電流三閉環控制

1.2.1 永磁同步電機數學模型

永磁同步電機（PMSM）是一個非線性、多變量的系統，經過坐標變換后，即可轉化為在坐標系下的數學模型。

PMSM電壓方程為

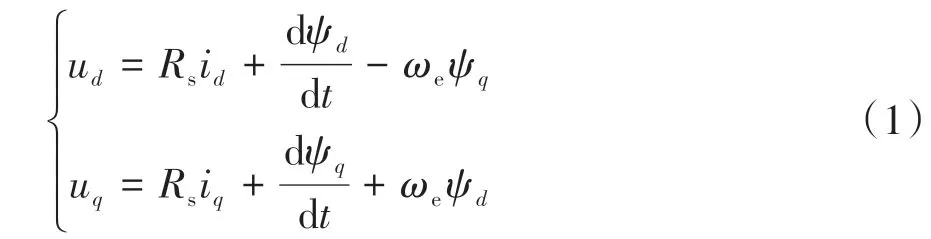
式中：u、u為定子電壓在軸上的分量；i、i為定子電流在軸上的分量；ψ、ψ為定子磁鏈在軸上的分量；=為轉子的電角速度，為電機極對數，為轉子機械角速度；為定子繞組的電阻。

磁鏈方程為

式中：L、L為定子繞組在軸上的電感分量；為永磁體磁鏈。

PMSM機械特性如下：

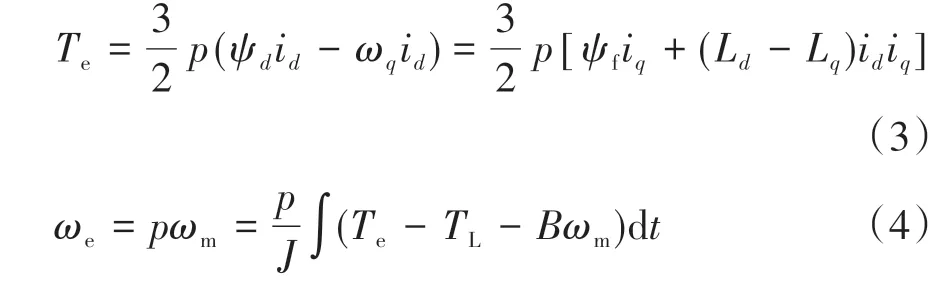
式中：為轉動慣量；為摩擦因數；為負載轉矩；為電磁轉矩。

綜上得到計算電機軸電流和機械角速度的微分方程為

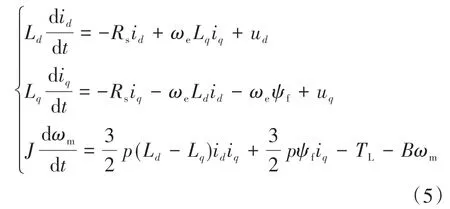
通過上式建立電機參數模型，u、u、為輸入，計算電機i、i、轉速、轉矩、轉角。

1.2.2 行星齒輪減速機構數學模型

式中：為行星架輸出轉矩；為太陽輪的輸入轉矩；為傳動比；為行星齒輪的傳動效率。傳動比過小，電機的尺寸較大，空間難以滿足要求，傳動比過大，行星齒輪發熱嚴重，經過對比，本文選定傳動比為5.503。

1.2.3 滾珠絲桿副數學模型

式中：為滾珠絲桿的驅動轉矩；為絲桿推力；為絲桿導程；為滾珠絲桿的傳動效率。

2 再生制動控制策略

2.1 前后軸制動力分配和電機機械制動力分配

在制動時，前后輪同時抱死，此時前后軸制動力F、F分配關系對應的曲線稱為I 曲線，而F與F的關系式為

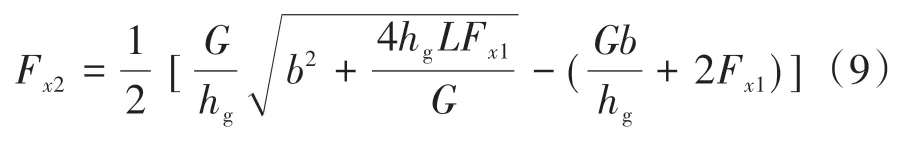
同時參考聯合國歐洲經濟委員會制定的ECE R13 制動法規，為保證制動時汽車有足夠的制動效率和穩定性，對雙軸汽車的前后軸制動器制動力提出了明確的要求：

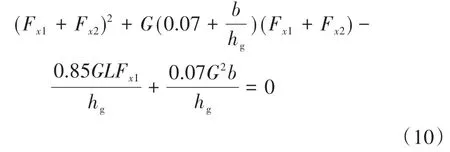
式中：F為前軸制動力；F為后軸制動力；為汽車質心高度；為前軸到后軸的距離；為后軸到質心的距離；為汽車重力。

同時，制動力矩和制動壓強之間存在關系為

式中：為當前汽車所需的制動轉矩；為當前汽車機械制動器所需的制動壓強；為制動缸活塞的面積；為制動器制動效率；為制動器摩擦因數；為制動盤的有效摩擦半徑；為制動器特定因素，是一個取決于制動器設計的因素。對于盤式制動器，取1，對于鼓式制動器，通常大于1。

制動強度為

式中：為整車質量；為車輪半徑。

前后軸制動力分配曲線如圖2所示。

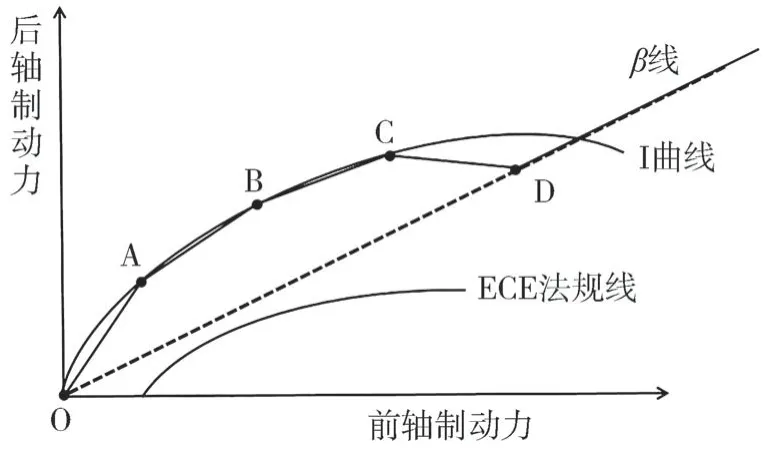
圖2 前后軸制動力分配

I曲線上已知制動強度的點滿足式（13）。

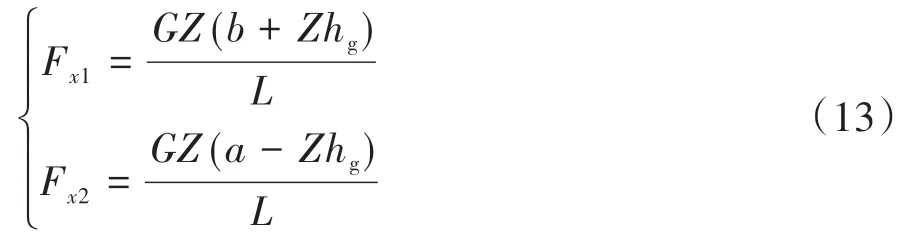
O 為原點，A 是I 曲線上制動強度0.2 的點，按式（13）算得點A 在圖2 中的坐標F，F，此時OA 線段的斜率為=F/F，得線段OA 上制動力分配為

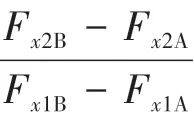
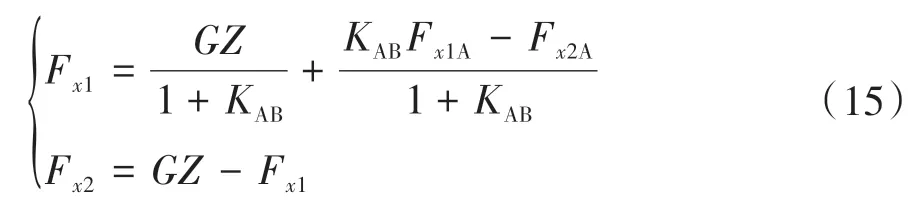
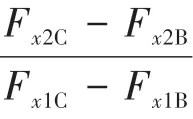
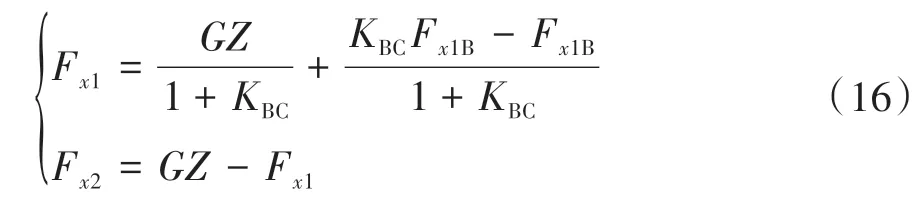
D 是線上制動強度＝0.75 的點，線上已知制動強度的點滿足式（17）。

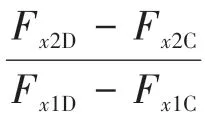
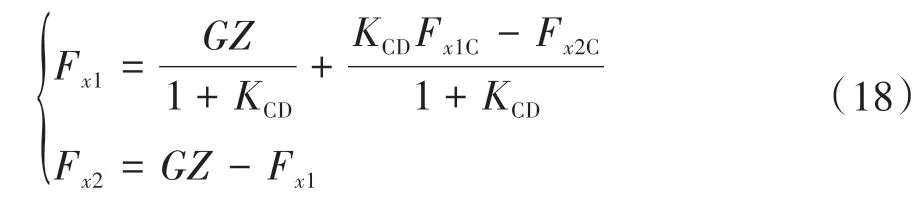
當制動強度＞0.75 時，認為是緊急制動，退出再生制動模式，為保證緊急制動時前后軸能夠迅速精準分配，前后軸制動力分配按照線分配：

2.2 再生制動模糊控制器設計

模糊控制是一種智能控制，主要用來解決復雜非線性問題。模糊控制器基本結構見圖3。

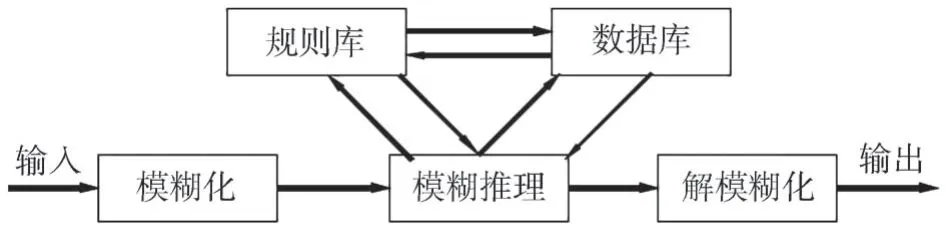
圖3 模糊邏輯控制器結構

2.2.1 輸入輸出變量選擇

該控制器3 個輸入量分別為制動踏板行程（%）、電池的（%）和車速（km/h）。輸出量是再生制動占比系數。通過制動踏板行程，根據AVL Cruise 軟件中制動踏板行程與制動壓強的關系，再結合式（11）可算出車輛需求的制動轉矩、車速和電池的SOC值同樣影響電機的再生制動轉矩。

2.2.2 輸入模糊化

采用Mamdani 推理方法。制動踏板行程（%）的模糊論域設置成［0，100］，相對應分成3 個模糊子集｛高（G），中（Z），低（D）｝；電池值（%）的模糊論域設置成［0，100］，相對應分成3 個模糊子集｛高（G），中（Z），低（D）｝；車速（km/h）的模糊論域設置成［0，140］，相對應分成4 個模糊子集｛高（G），中（Z），低（D），很低（HD）｝。

2.2.3 輸出反模糊化

輸出量是再生制動占比系數，取其模糊論域為［0，1］，分為5 個模糊子集｛很高（HG），高（G），中（Z），低（D），很低（HD）｝。

2.2.4 模糊控制規則

制動踏板行程越大，表示制動需求越大，為保證安全，再生制動占比應減小；電池值越大，為防止過充，保護電池壽命，再生制動占比應減小。由此制動模糊控制規則如表1所示。

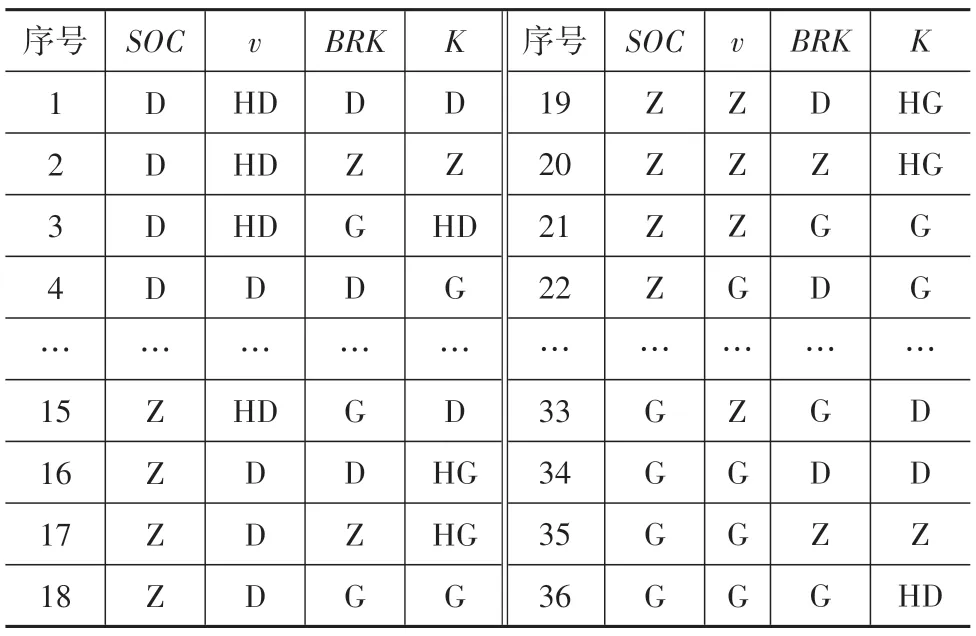
表1 模糊控制規則

2.3 PSO算法對模糊隸屬度函數的優化

粒子群算法是從鳥類族群覓食的訊息傳遞所得到的一個啟發，族群中的每只鳥都相當于一個粒子個體，它們有自己的記憶，通過移動產生記憶積累經驗，并依此調整自身的移動方向和速度。多個粒子同時移動，且相互學習經驗，由此相互比較得到最優解，同時整個群體擁有學習性、記憶性，從而也影響粒子達到最佳狀態。

模糊控制設計簡單，便于應用，且魯棒性強，適應于非線性時變系統。但由于模糊控制的隸屬度函數和模糊控制規則往往依據經驗而不夠準確，無法獲得全局最優。而粒子群優化（PSO）算法是一種結構簡單、收斂速度較快且能在個體與社會性之間尋求平衡的隨機全局優化算法，可以提高模糊控制的準確性。將需要優化的參數設置為｛，，…，，｝。設置最大迭代次數為50，每代的粒子數量為20個，粒子的最大速度為0.1 m/s。以最大化制動回收能量為目標函數進行優化。優化前的隸屬度函數如圖4所示，優化后的隸屬度函數如圖5所示。

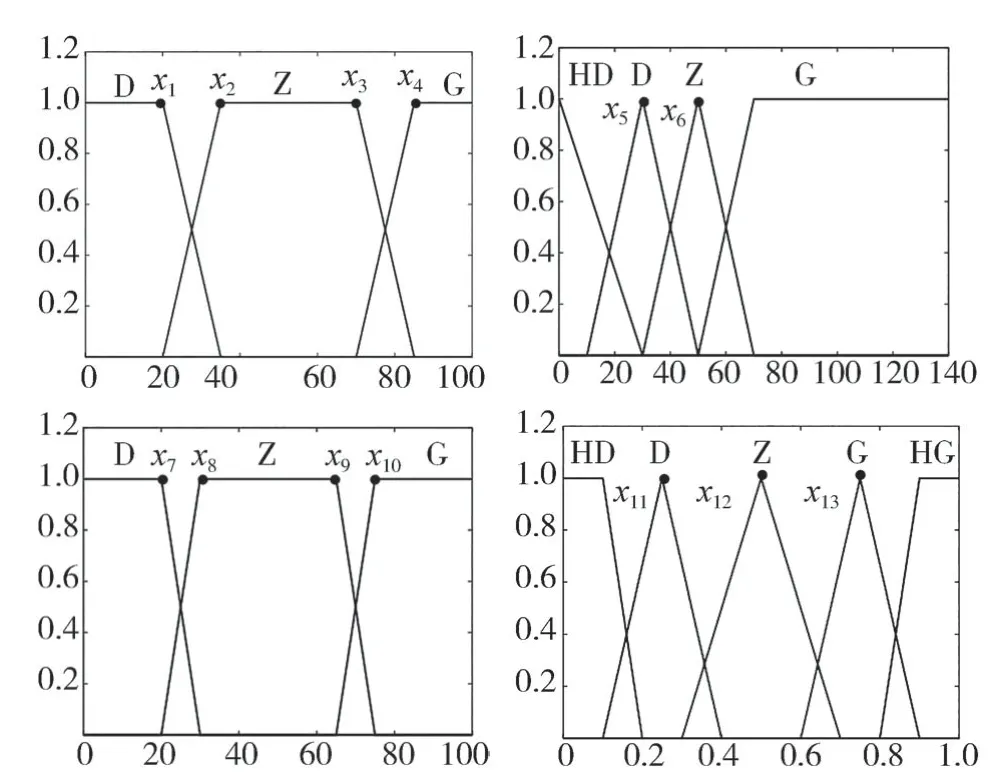
圖4 優化前模糊控制隸屬度函數圖

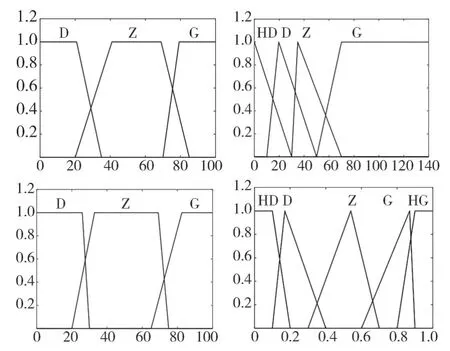
圖5 優化后模糊控制隸屬度函數圖

2.4 約束條件

2.4.1 電機轉矩特性限制

采用4 個永磁同步電機，當電機轉速低于額定轉速時，電機處于恒轉矩階段，最大制動轉矩為；當電機轉速高于額定轉速時，電機處于恒功率階段。輪轂電機最大再生制動力為

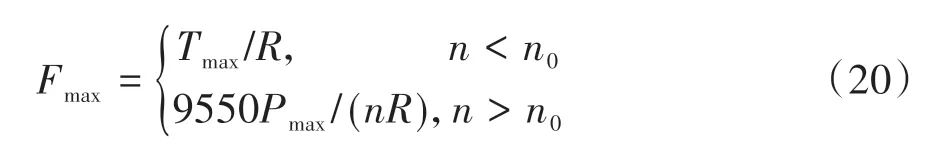
式中：為電機能提供的最大再生制動力，N；為電機提供的最大轉矩，N·m；為車輪半徑，m；為電機轉速，r/min；為電機額定轉速，r/min；為電機最大功率，kW。

2.4.2 電池SOC的限制

為保護電池，防止電池過充，當＞85%時，就應退出再生制動模式，轉為純機械制動。

2.4.3 汽車車速的限制

當汽車車速很低時，電機轉動很慢，產生的充電電流很小，為使車輛盡快停車，當車速低時退出再生制動模式，轉為純機械制動。本文設置限制車速為5 km/h，當車速低于該值，便退出再生制動。同時為使再生制動和機械制動的交替平緩進行，設置一個速度影響因子K：

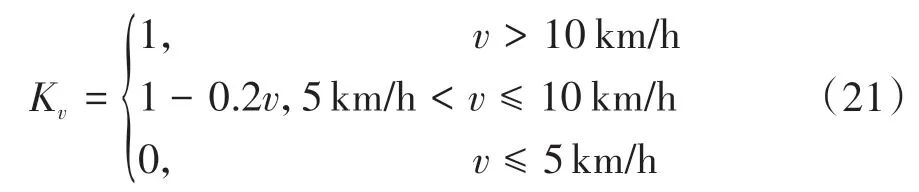
最終的電機再生制動力占比系數為K×K。電機的再生制動力等于分配到每個軸上的需求制動力乘上約束后的占比系數K×K。經過前后軸制動力分配得到前后軸的需求制動力，然后檢測每個軸的再生制動力是否能夠滿足需求，如果不能，則利用機械制動力作為補充。

2.5 再生制動過程分析

收到駕駛員制動信號后，根據式（12）計算制動強度，同時根據當前車速和電池值判斷是否進行再生制動。若不符合條件，結合圖2，得到前后軸需求制動力，利用EMB 系統進行純機械制動。若符合條件，結合圖2，得到前后軸制動力，再輸入模糊控制器，得到所需再生制動力，同時與輪轂電機最大再生制動力進行比較：如果大于，則完全由電機提供制動力；如果小于，則利用EMB 系統進行補充。整個流程見圖6。

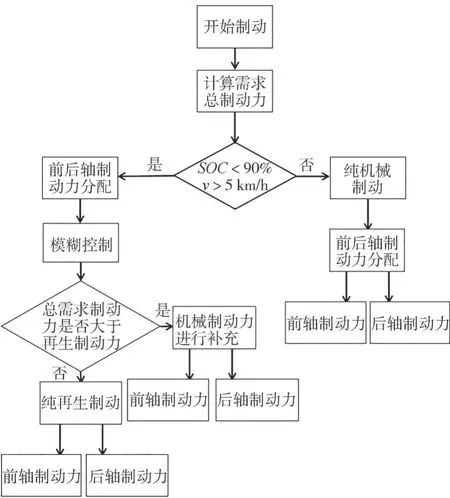
圖6 控制流程圖

3 建模仿真

為驗證優化控制策略的可行性和回收效果，利用Simulink 和AVL Cruise 搭建聯合仿真平臺。利用Simulink 搭建EMB 數學模型和控制策略模型仿真，利用Cruise 搭建整車模型、電機模型、電池模型等，搭建好的整車模型如圖7 所示，搭建好的控制策略模型如圖8 所示。通過將Simlink 模型編譯成DLL文件接入Cruise 軟件中，實現聯合仿真。整車模型參數如表2所示。

表2 整車模型參數

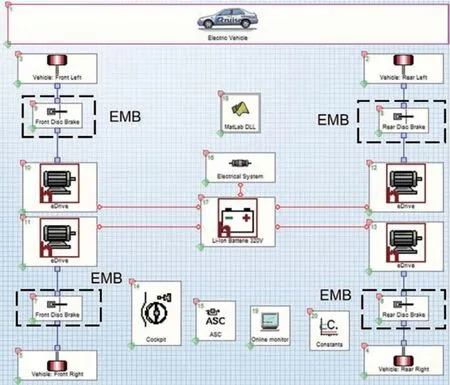
圖7 整車模型圖

圖8 控制策略模型圖

4 仿真結果分析

本文中的純電動汽車采用4 個輪轂電機。在AVL Cruise 中設置仿真工況，分別在典型的NEDC工況和中國城市工況CLTC-P 下進行仿真驗證，且利用傳統的固定比例回收控制策略進行對比。

4.1 NEDC工況仿真結果分析

NEDC（new European driving cycle）是歐洲的續航測試工況標準，包含4 個市區循環和1 個郊區循環。用本文制定的優化模糊控制策略與優化前的模糊控制策略和經典的固定比例控制策略進行對比，比較制動回收能量和電池SOC值的變化。

圖9 為NEDC 速度圖，圖10 為優化前后再生制動占比系數圖，圖11 為NEDC 工況下電機和機械制動的轉矩圖。圖中的機械轉矩數值較大是因為此時車速低于2.4.3 節中的限定值，汽車逐漸退出再生制動，變為純機械制動。圖12 為整個NEDC 工況下仿真的SOC 變化圖，圖13 為整個NEDC 工況下回制動收到能量。仿真結果數據如表3 所示。由圖12、圖13 和表3 可以看出，在NEDC 工況下，通過PSO 算法優化后模糊控制策略再生的制動回收能量最多，比固定比例控制策略多了52.69%，比優化前的模糊控制策略多了2.5%。

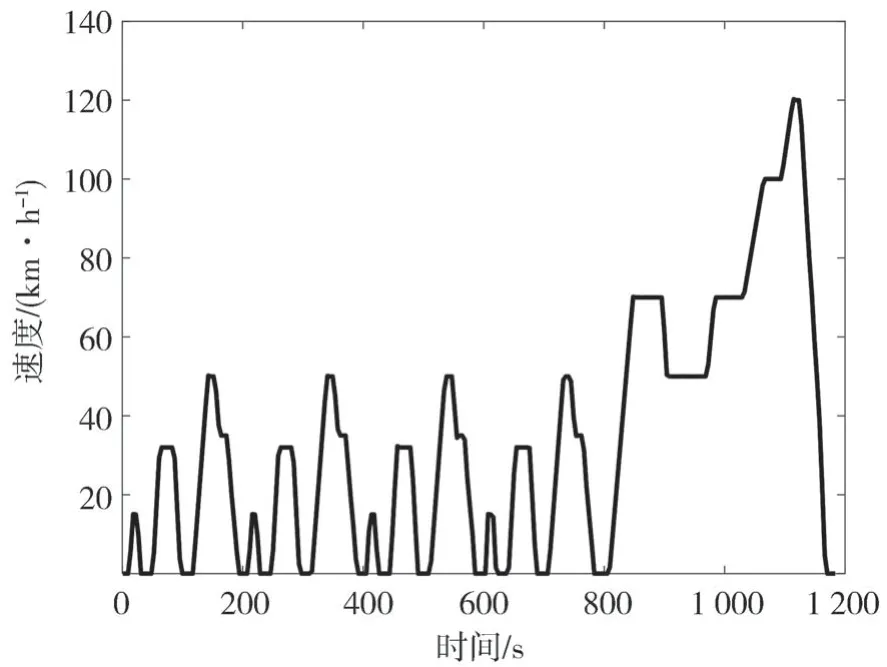
圖9 NEDC速度圖

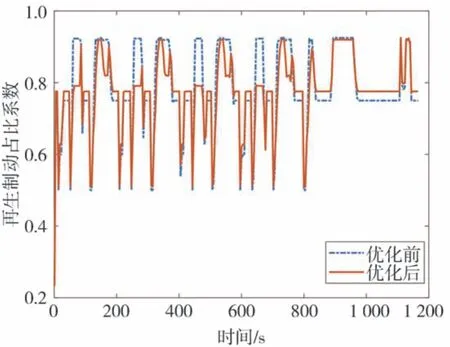
圖10 再生制動占比系數圖

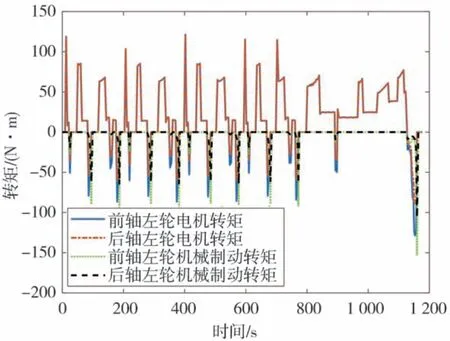
圖11 NEDC工況轉矩圖

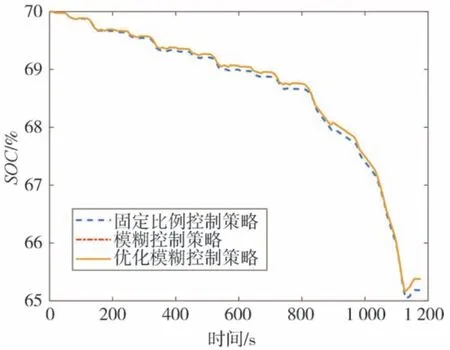
圖12 NEDC仿真工況下SOC變化

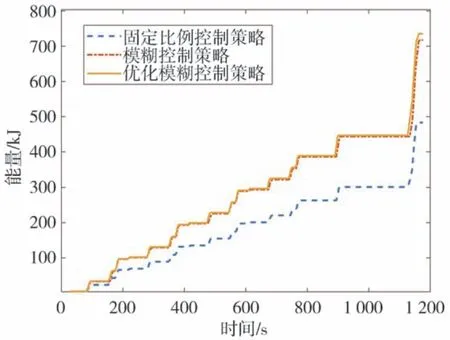
圖13 NEDC仿真工況下回收能量

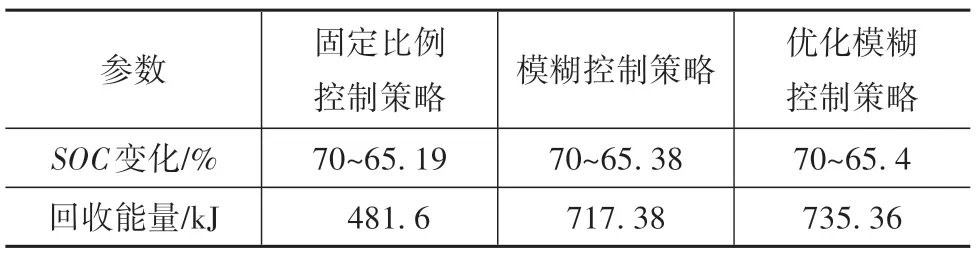
表3 NEDC工況仿真結果

4.2 CLTC-P工況仿真結果分析

CLTC-P（China light-duty vehicle test cyclepassenger）是基于41 座城市、5 000 多輛車，累積5 000 多萬km、20 億條低頻交通動態大數據定義的標準工況。CLTC 更真實反映了具有中國特色、高度契合中國交通實際情況的工況，包括更為寬泛的駕駛工況、更為合理的平均車速和停車模式比例以及更為豐富的動態加減速工況。

圖14 為CLTC-P 速度圖，圖15 為優化前后再生制動占比系數圖，圖16 為CLTC-P 工況下電機和機械制動的轉矩圖。圖中的機械轉矩數值較大是因為此時車速低于2.4.3 節中的限定值，汽車逐漸退出再生制動，變為純機械制動。圖17 為整個CLTC-P工況下仿真的SOC 變化圖，圖18 為整個CLTC-P 工況下制動回收能量，仿真結果數據如表4 所示。由圖17、圖18 和表4 可以看出，在CLTC-P 工況下，通過PSO算法優化后模糊控制策略的再生制動回收能量最多，比固定比例控制策略多了47.34%，比優化前的模糊控制策略多了1.56%，從而驗證了本文控制策略的有效性。

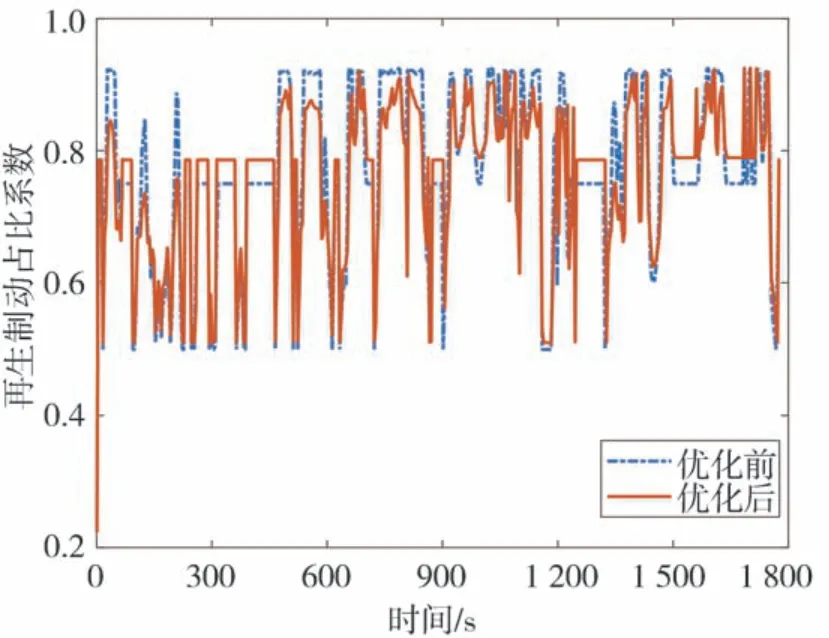
圖15 再生制動占比系數圖

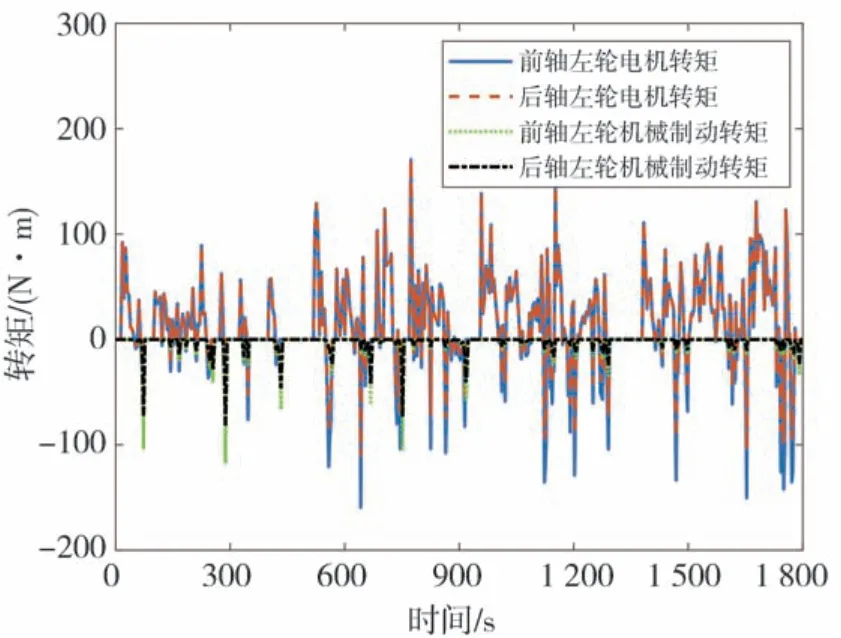
圖16 CLTC-P工況轉矩圖

圖17 CLTC-P仿真工況下SOC變化

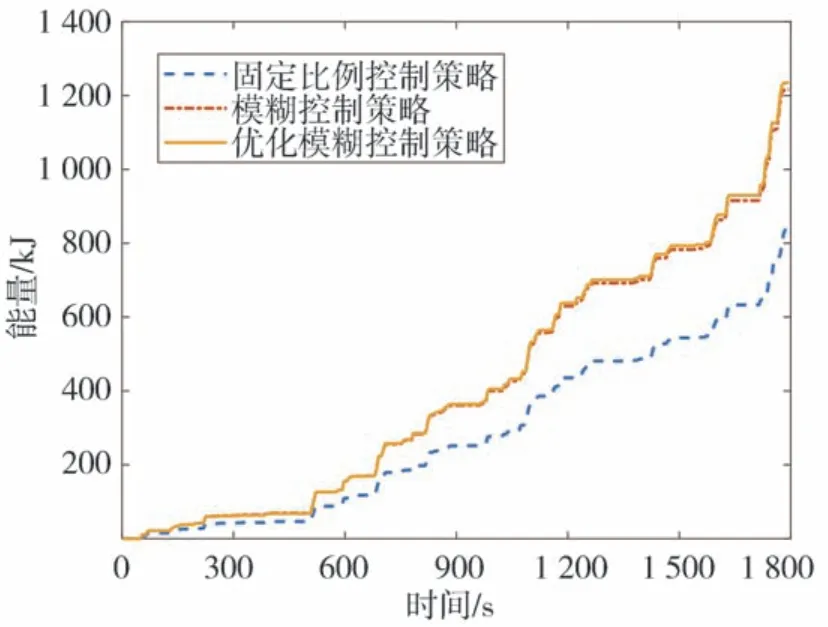
圖18 CLTC-P仿真工況下能量回收

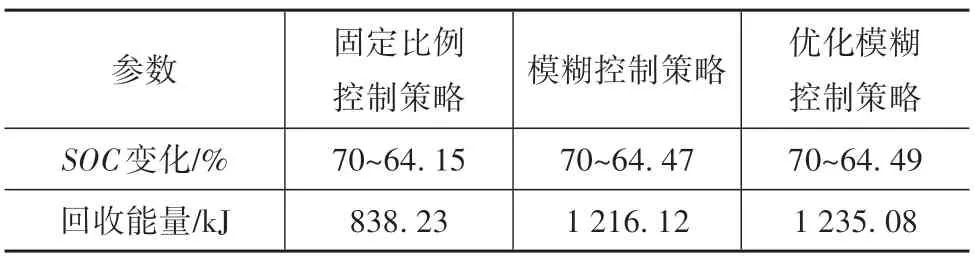
表4 CLTC-P工況仿真結果

圖14 CLTC-P速度圖

5 結論

（1）采用響應迅速、反應靈敏的電子機械制動系統代替傳統的液壓制動系統，使制動更加高效，更有利于配合制動控制策略。

（2）基于電子機械制動系統，考慮ECE 法規、電池SOC 值和車速等約束條件，同時采用了模糊控制器，并利用粒子群算法進行優化。再用Simulink 和AVL Cruise 軟件進行聯合仿真，在NEDC 和CLTC-P兩種典型工況下進行對比。結果表明，該純電動汽車在本文的控制策略下再生制動回收能量最多。