改進(jìn)遺傳算法及其在倒立擺控制中應(yīng)用研究

董如意，劉亞男

(吉林化工學(xué)院 信息與控制工程學(xué)院，吉林 吉林 132022)

遺傳算法[1-2](Genetic Algorithm,GA)是目前應(yīng)用范圍最廣的元啟發(fā)式算法之一，通過模擬生物“優(yōu)勝劣汰、適者生存”的自然法則，采用并行的概率搜索機(jī)制，尋找適應(yīng)度函數(shù)值的最優(yōu)化結(jié)果，對(duì)目標(biāo)函數(shù)沒有過多限制，具有良好的全局搜索能力[3].但標(biāo)準(zhǔn)遺傳算法中交叉算子和變異算子使用的是固定數(shù)值，導(dǎo)致尋優(yōu)過程中種群多樣性下降，過早收斂于局部最優(yōu)解，嚴(yán)重影響了最優(yōu)解的質(zhì)量和搜索速度.在眾多對(duì)遺傳算法的研究中，使用數(shù)學(xué)計(jì)算方法來克服傳統(tǒng)算法對(duì)初始信息極其敏感的缺點(diǎn)，取得了較大的成功[4]，然而大多改進(jìn)方法目前僅集中在理論研究方面，對(duì)于實(shí)際工程問題的求解還需要進(jìn)一步完善.因此，結(jié)合數(shù)學(xué)方法，針對(duì)傳統(tǒng)遺傳算法本身存在的缺點(diǎn)，設(shè)計(jì)了一種自適應(yīng)調(diào)整交叉和變異的遺傳算法，同時(shí)將改進(jìn)的遺傳算法應(yīng)用于倒立擺控制器的設(shè)計(jì)中，實(shí)驗(yàn)表明，相比于傳統(tǒng)遺傳算法，改進(jìn)的遺傳算法對(duì)倒立擺系統(tǒng)關(guān)鍵參數(shù)的尋優(yōu)效果更好，倒立擺達(dá)到穩(wěn)定的次數(shù)更多.

1 遺傳算法及改進(jìn)

1.1 標(biāo)準(zhǔn)遺傳算法

遺傳算法是1975年由Holland提出的一種隨機(jī)的并行搜索算法，主要模擬生物群體在自然選擇中的作用機(jī)理和繁衍過程，包括生物增殖、雜交和基因突變等遺傳現(xiàn)象.與其他數(shù)值優(yōu)化算法相比，遺傳算法具有很好的全局收斂性和普適性，廣泛應(yīng)用于人工智能、工業(yè)優(yōu)化、數(shù)學(xué)求解以及相關(guān)工程實(shí)踐中.

標(biāo)準(zhǔn)遺傳算法是基于非確定性的概率搜索機(jī)制，將問題的可行解進(jìn)行二進(jìn)制編碼，模擬生物的染色體特征，通過計(jì)算適應(yīng)度值的來保留最佳的可行解，然后按照一定的概率完成染色體的交叉和變異，再以精英選擇的方式保留最優(yōu)個(gè)體的特征，以此不斷迭代，直到找到全局適應(yīng)度值最優(yōu)的可行解.標(biāo)準(zhǔn)遺傳算法的優(yōu)化流程圖如圖1所示.

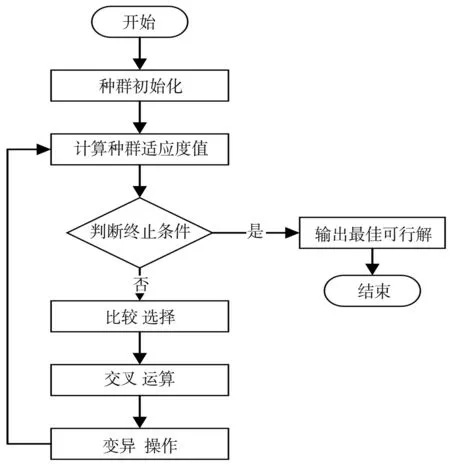
圖1 標(biāo)準(zhǔn)遺傳算法流程圖

盡管遺傳算法具有操作簡(jiǎn)單、實(shí)用性強(qiáng)的特點(diǎn)，同時(shí)也存在明顯的不足，例如局部搜索能力差、容易早熟、后期收斂速度慢、收斂精度低等.特別是標(biāo)準(zhǔn)遺傳算法的交叉率和變異率為固定的數(shù)值，會(huì)導(dǎo)致在算法優(yōu)化的后期使種群失去多樣性的優(yōu)勢(shì)，面對(duì)較復(fù)雜的目標(biāo)函數(shù)時(shí)，嚴(yán)重影響算法的性能.因此，針對(duì)標(biāo)準(zhǔn)遺傳算法的缺點(diǎn)，結(jié)合數(shù)學(xué)理論，提出了一種改進(jìn)的遺傳算法.

1.2 改進(jìn)遺傳算法

中改進(jìn)的遺傳算法主要解決以下幾個(gè)問題：

1.在最初迭代中，交叉率、變異率均不能降為零，又要提高對(duì)最優(yōu)解的搜索速度.

2.當(dāng)平均適應(yīng)度值與最大適應(yīng)度值的差值較大時(shí)，迭代過程不會(huì)出現(xiàn)線性變化，有效避免種群進(jìn)化遲緩或停滯.

3.算法后期，為了保留優(yōu)良個(gè)體，在滿足精度的情況下，緩慢減小交叉率和變異率.

基于上述問題，對(duì)交叉率、變異率等特征進(jìn)行了一系列非線性的、可自適應(yīng)性的優(yōu)化調(diào)整，以此來提升算法的優(yōu)化能力.首先，利用sigmoid函數(shù)對(duì)交叉率進(jìn)行改進(jìn)，該函數(shù)的數(shù)學(xué)模型為S形曲線，增長(zhǎng)趨勢(shì)會(huì)隨參數(shù)的變化而逐漸平緩，簡(jiǎn)化方程如式(1)所示.

(1)

sigmoid函數(shù)的仿真曲線圖2所示.

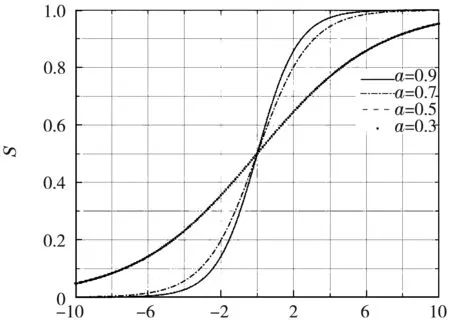
x圖2 sigmoid函數(shù)曲線圖

通過基于sigmoid函數(shù)的自適應(yīng)調(diào)節(jié)，遺傳算法的交叉率在前期迭代過程中保持最大值，增加個(gè)體的多樣性，提高尋優(yōu)過程的全局搜索能力，經(jīng)過一定次數(shù)的迭代后，交叉率會(huì)逐漸降低至最小值，從而完成全局搜索向局部搜索的平穩(wěn)過渡，由改進(jìn)的式(2)可知，Pc中favg和fmax隨sigmoid函數(shù)進(jìn)行非線性調(diào)整.

(2)

其中，f是個(gè)體適應(yīng)度；favg是適應(yīng)度值的平均值；fmax是適應(yīng)度值的最大值；fmin是適應(yīng)度值的最小值；f′代表在交叉?zhèn)€體中擇優(yōu)選取；k1是曲線平滑參數(shù)；Pc max，Pc min是交叉率的最大值和最小值.

為了進(jìn)一步提高遺傳算法的局部搜索能力，采用一種新的變異方式，即十進(jìn)制變異法.Pm按照個(gè)體適應(yīng)度值從小到大排序，較優(yōu)秀的個(gè)體排在后邊，把選擇的優(yōu)秀個(gè)體轉(zhuǎn)成十進(jìn)制，然后以循環(huán)方式加上遞增的十進(jìn)制數(shù)，該十進(jìn)制數(shù)由當(dāng)前變異率的最大值和最小值確定，最后選擇一個(gè)最優(yōu)個(gè)體進(jìn)行變異.十進(jìn)制變異法可以在一定程度上增加變異的隨機(jī)性，擴(kuò)展變異的范圍和概率，讓尋優(yōu)結(jié)果可以更好地跳出局部最優(yōu)解，保證收斂速度的同時(shí)提升算法的精確度.變異過程的調(diào)節(jié)如式(3)所示.

(3)

其中，T為最大迭代次數(shù)；t為當(dāng)前迭代次數(shù)；Pm max，Pm min為變異率的最大值和最小值.

2 基于遺傳算法的倒立擺智能控制

2.1 直線一級(jí)倒立擺的數(shù)學(xué)模型

倒立擺系統(tǒng)是一種十分經(jīng)典的工程欠驅(qū)動(dòng)體系[5]，是控制、數(shù)學(xué)、力學(xué)等理論的有機(jī)結(jié)合和綜合應(yīng)用.由于倒立擺系統(tǒng)具有高階非線性、自然不穩(wěn)定等在復(fù)雜工程中也十分普遍的特性[6]，其相關(guān)控制算法的研究在機(jī)器人、智能控制[7]以及其他諸多領(lǐng)域均有所應(yīng)用.因此，將倒立擺控制作為研究的控制對(duì)象，具有很好的數(shù)學(xué)理論實(shí)踐意義和技術(shù)工程分析指導(dǎo)研究意義[8-9].

由于直線一級(jí)倒立擺自身具有非線性及不穩(wěn)定性，可以適當(dāng)忽略個(gè)別次要因素，例如角度細(xì)小偏差、系統(tǒng)摩擦力等，從而簡(jiǎn)化該運(yùn)動(dòng)系統(tǒng).倒立擺控制系統(tǒng)的數(shù)學(xué)模型如圖3所示.

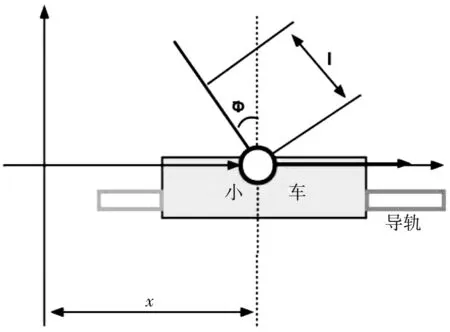
圖3 直線一級(jí)倒立擺的結(jié)構(gòu)示意圖

2.2 倒立擺控制模型

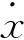
圖4 倒立擺控制模型

遺傳算法優(yōu)化倒立擺系統(tǒng)的流程如下：

1.隨機(jī)產(chǎn)生初始種群.

2.按照指定策略判斷參數(shù)的適應(yīng)度是否達(dá)到優(yōu)化準(zhǔn)則或終止條件，若可行，輸出最優(yōu)解，判斷結(jié)束；否則，進(jìn)行下一步.

3.依據(jù)適應(yīng)度值選擇父代種群，選擇適應(yīng)度較高的參數(shù)，適應(yīng)度較低的參數(shù)被淘汰.

4.按照一定的方法對(duì)父代的染色體進(jìn)行交叉操作，生成子代.

5.對(duì)子代染色體進(jìn)行變異操作.

6.交叉和變異產(chǎn)生新一代種群，隨即重復(fù)執(zhí)行步驟2，直到產(chǎn)生最優(yōu)可行解.

3 仿真結(jié)果與分析

3.1 模型參數(shù)

使用固高公司開發(fā)的倒立擺系統(tǒng)模型，模型具體參數(shù)如表1所示.

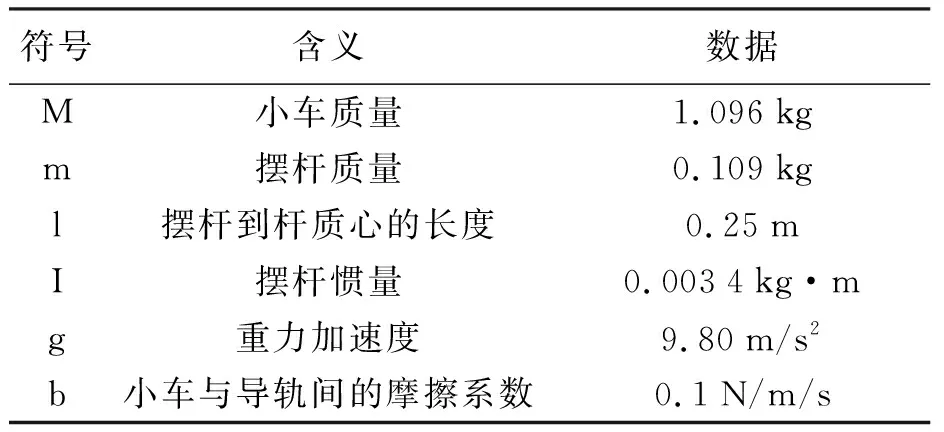
表1 實(shí)際模型參數(shù)

3.2 數(shù)據(jù)分析

在改進(jìn)遺傳算法優(yōu)化倒立擺系統(tǒng)的問題上，種群大小、迭代次數(shù)、交叉、遺傳算子對(duì)倒立擺系統(tǒng)的優(yōu)化效果都有著一定的影響，而重點(diǎn)研究基于sigmoid函數(shù)的自適應(yīng)調(diào)整的交叉率和基于十進(jìn)制的變異率對(duì)倒立擺穩(wěn)定性的影響.因此采用控制變量法，設(shè)置種群大小為20，迭代次數(shù)為200次，在Python3.8上進(jìn)行仿真實(shí)驗(yàn)，比較標(biāo)準(zhǔn)遺傳算法和改進(jìn)遺傳算法的優(yōu)化能力.

表2對(duì)比分析了標(biāo)準(zhǔn)遺傳算法下恒定的交叉率和變異率與改進(jìn)遺傳算法的自適應(yīng)調(diào)整交叉率和變異率的區(qū)別，從表中可以清楚地體現(xiàn)出，改進(jìn)后的遺傳算法對(duì)倒立擺的穩(wěn)定效果更好.

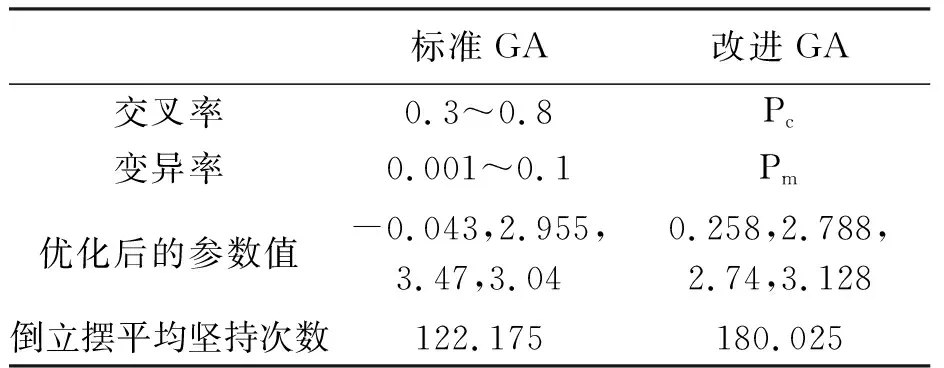
表2 標(biāo)準(zhǔn)遺傳算法與改進(jìn)遺傳算法對(duì)比

表3為表2的進(jìn)一步解釋說明，是在不同迭代次數(shù)下的參數(shù)值，隨著迭代次數(shù)的增加，優(yōu)化后的參數(shù)值效果更好，倒立擺的穩(wěn)定效果更好.

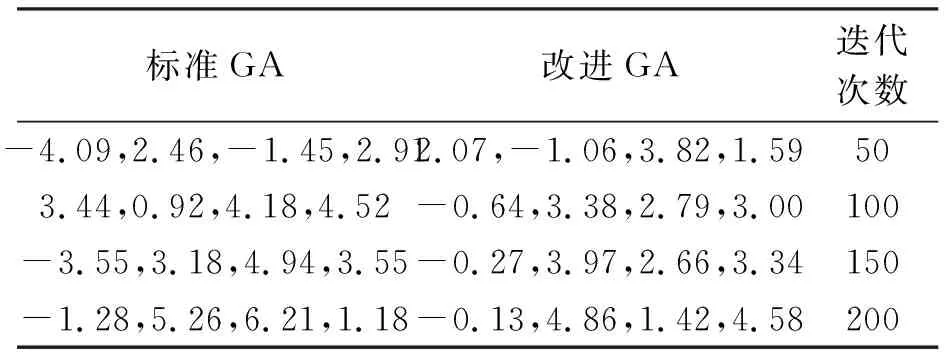
表3 優(yōu)化后的參數(shù)值

圖5為兩種算法在不同迭代次數(shù)下的倒立擺堅(jiān)持次數(shù)的折線圖，從中可清晰看出，標(biāo)準(zhǔn)遺傳算法對(duì)倒立擺穩(wěn)定控制參數(shù)的優(yōu)化效果并不理想，結(jié)果有大提升空間.改進(jìn)遺傳算法下倒立擺堅(jiān)持的次數(shù)明顯提高，隨著迭代次數(shù)的不斷增大，倒立擺的穩(wěn)定效果更好.

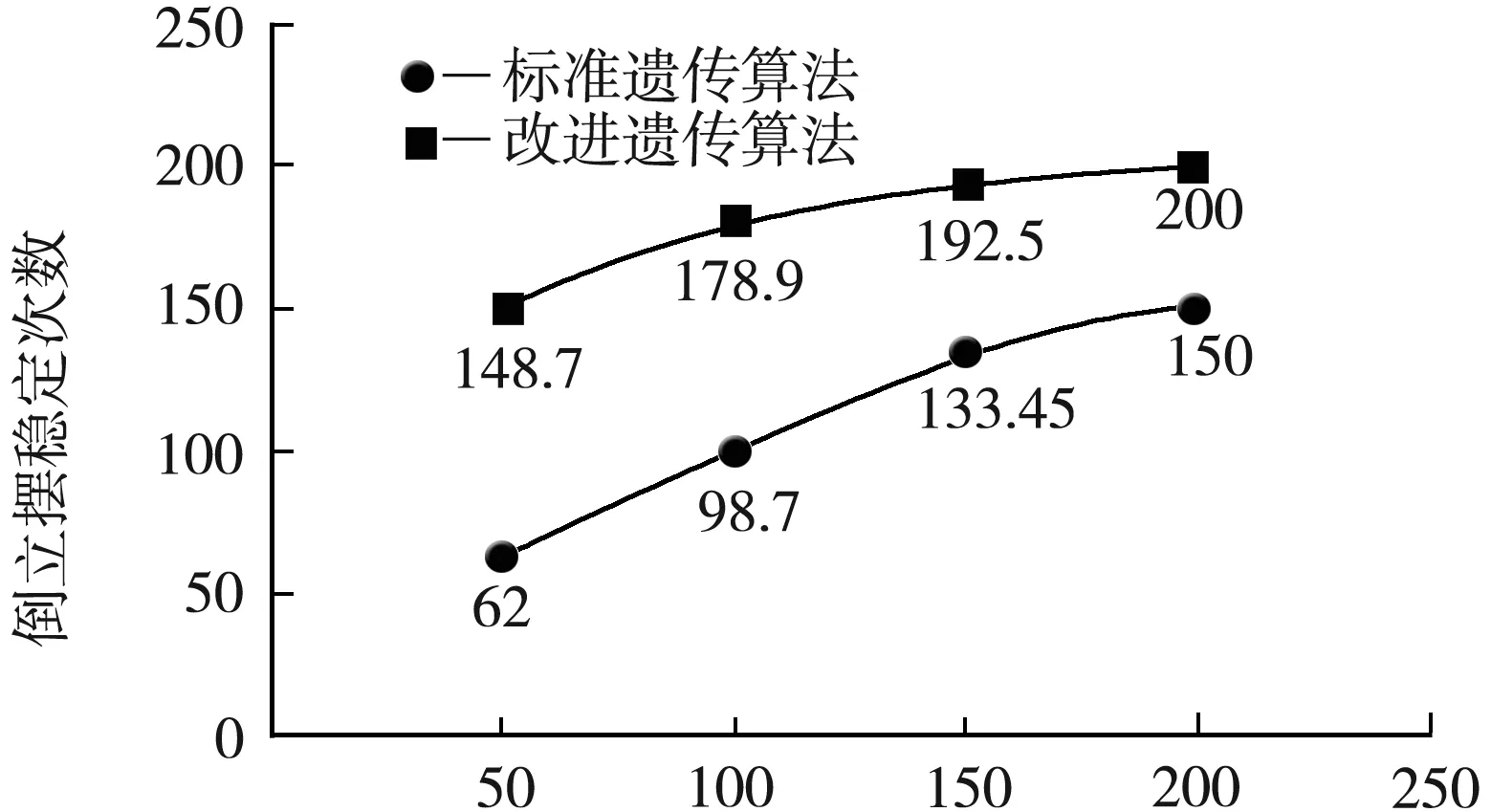
迭代次數(shù)圖5 倒立擺堅(jiān)持次數(shù)折線圖

該實(shí)驗(yàn)的仿真結(jié)果表明，改進(jìn)的遺傳算法在實(shí)際測(cè)試上展現(xiàn)了良好的可行性，能夠更好、更快地找到優(yōu)質(zhì)可行解.經(jīng)過多輪200次迭代測(cè)試下，改進(jìn)的遺傳算法相比標(biāo)準(zhǔn)遺傳算法對(duì)倒立擺的穩(wěn)定控制效果更好，即該倒立擺已經(jīng)實(shí)現(xiàn)穩(wěn)定控制.

4 結(jié) 論

通過分析標(biāo)準(zhǔn)遺傳算法中交叉算子和變異算子的特點(diǎn)，分別對(duì)二者進(jìn)行了自適應(yīng)調(diào)整，利用sigmoid函數(shù)實(shí)現(xiàn)了前期全局搜索向后期局部搜索的平穩(wěn)過渡，彌補(bǔ)了標(biāo)準(zhǔn)遺傳算法種群多樣性降低和搜索速度遲緩等不足.十進(jìn)制變異方法在保留了最優(yōu)個(gè)體的同時(shí)，增大了個(gè)體跳出局部最優(yōu)的能力，避免了算法早熟，提升了最優(yōu)解的品質(zhì).以直線一級(jí)倒立擺智能控制系統(tǒng)作為主要研究對(duì)象,基于改進(jìn)的遺傳算法對(duì)倒立擺智能控制系統(tǒng)進(jìn)行參數(shù)優(yōu)化，并通過仿真實(shí)驗(yàn)得出，相較于原始遺傳算法，改進(jìn)的遺傳算法在倒立擺穩(wěn)定控制上的優(yōu)化效果更好.