基于雙向長短期記憶循環神經網絡的網絡流量預測

杜秀麗 范志宇 呂亞娜 邱少明

1(大連大學通信與網絡重點實驗室 遼寧 大連 116622) 2(大連大學信息工程學院 遼寧 大連 116622)

0 引 言

隨著互聯網的發展，網絡的異構性和復雜性不斷增強，而網絡的規劃、設計和運行都是以分析和預測網絡流量的特性為前提的。網絡流量預測對增強網絡性能、解決網絡擁堵、防止網絡入侵有著重要的作用。經過大量的研究發現：網絡流量表現出自相似特征、非平穩特征、長時間相關特征和突發性特征等[1-2]。

網絡流量預測方法主要有兩類：平穩預測方法和非平穩預測方法。平穩預測方法中馬爾可夫(Markov)模型[3]很容易構建，可以清晰地描述出整個過程，但增加模型的參數時將會存在很大的計算量。自回歸(Auto Regressive,AR)模型和自回歸滑動平均(Auto Regressive Moving Average,ARMA)模型[4]理論計算方法簡單且求解速度快，但無法有效描述網絡流量的非平穩特性。自回歸積分滑動平均(Auto Regressive Integrated Moving Average,ARIMA)模型[5]只能對流量變化不大或者流量變化存在規律的網絡流量進行預測。

網絡流量非平穩預測方法中，基于支持向量機(Support Vector Machine,SVM)的網絡流量預測方法[6-7]能夠解決網絡流量預測中小樣本、非線性、高維和局部極值等問題，但訓練樣本和自身網絡參數對預測結果的好壞影響很大。由于網絡流量在時頻域具有稀疏性，研究者將壓縮感知技術[8-9]引入網絡流量測量和預測中，將網絡流量預測問題轉變成重新構造網絡流量的問題，提高了預測的準確性。但是壓縮感知中網絡流量的分析和觀測矩陣的設計還有待進一步提高。為了能夠進一步解決網絡流量非線性的問題，專家學者們開始致力于研究基于深度學習的網絡流量預測方法[10]。Azzouni等[11]在此基礎上，提出了基于長短期記憶循環神經網絡(Long Short Term Memory,LSTM)的網絡流量預測方法，提高了預測的準確性。但長短期記憶循環神經網絡對網絡流量學習是按照單一方向進行的，導致越早學習部分特征遺忘得越多，起到的作用越小，忽略了天與天之間上下雙向的聯系，從而影響最終的預測結果。

針對以上存在的問題，為了能夠進一步提高網絡流量預測的準確性，本文提出一種基于雙向長短期記憶循環神經網絡(Bi-directional Long Short Term Memory,BiLSTM)的網絡流量預測方法。對網絡流量序列進行雙向學習，避免單向學習導致較早學習部分，特征提取和記憶效果差的問題。同時雙向學習可以充分挖掘網絡流量天與天之間雙向的聯系，完整地學習到網絡流量的整體特征，更好地進行網絡流量預測。

1 基于LSTM的網絡流量預測方法

長短期記憶循環神經網絡是由Hochreiter等[12]提出，Graves等[13]進行優化和推廣的一種改良后的循環神經網絡。LSTM神經網絡中擁有時間記憶單元，能夠對時間序列中長短期依賴的信息進行學習，從而對時間序列中的間隔和延遲事件進行處理和預測，因此可以利用LSTM神經網絡[14]對網絡流量進行預測。

1.1 LSTM網絡結構

LSTM神經網絡具有獨特的門限管理機制，一個能夠正常工作、操控和保護神經元的LSTM網絡具有三個門：輸入門(Input gate)、遺忘門(Forget gate)和輸出門(Output gate)。輸入門從外部獲取新的數據，同時對其進行處理。遺忘門決定網絡單元細胞狀態的遺忘程度，從而保留下來最具有特征的記憶細胞狀態。輸出門對LSTM單元計算出的結果進行選擇性輸出。LSTM單元的細胞狀態是網絡的靈魂，細胞狀態信息可以在網絡中進行傳送，不會影響到神經元的狀態。LSTM典型的網絡結構如圖1所示。

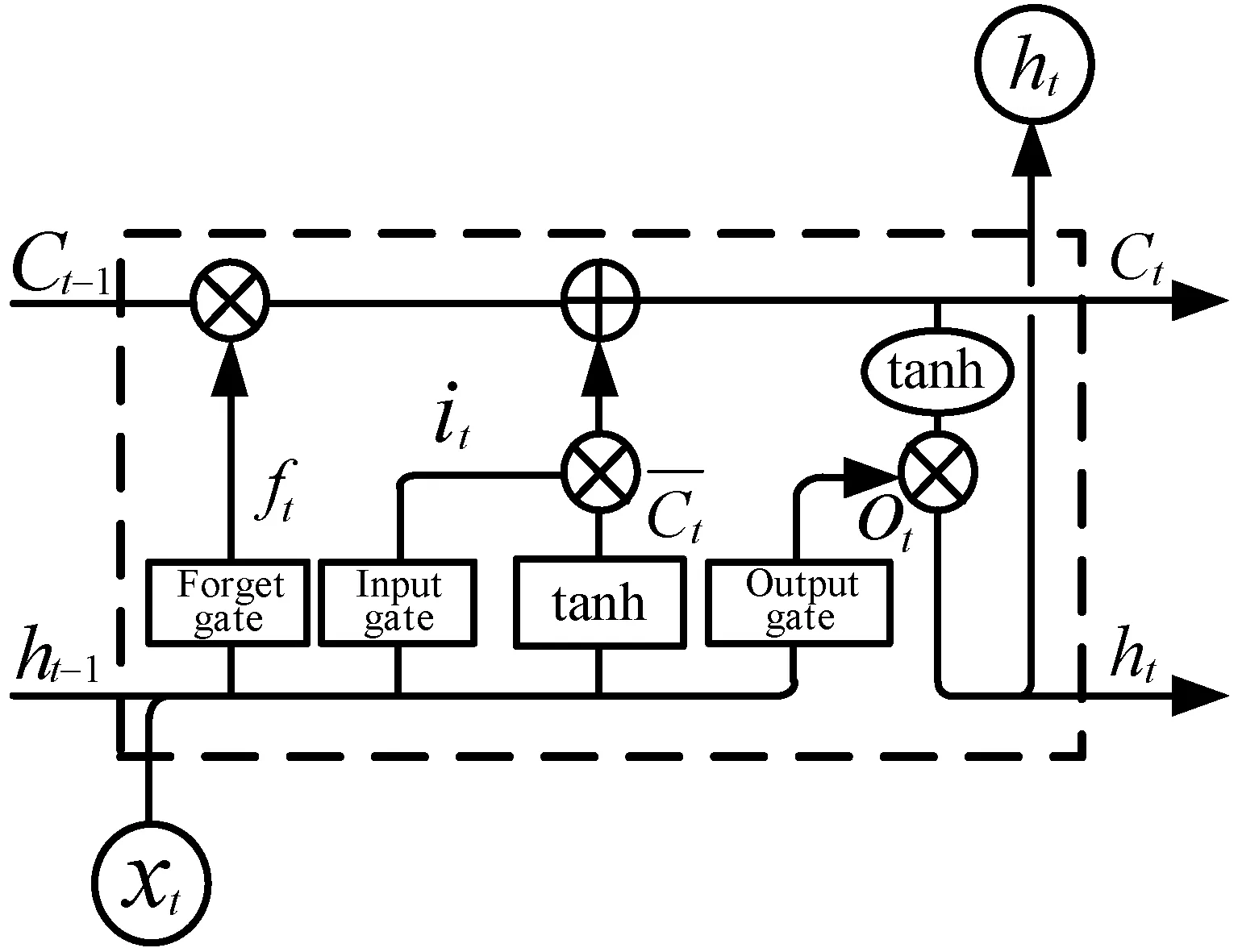
圖1 LSTM單元結構

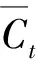
it=σ(Wu[ht-1,xt]+bu)

(1)

ft=σ(Wf[ht-1,xt]+bf)

(2)

Ot=σ(Wo[ht-1,xt]+bo)

(3)

(4)

(5)

ht=Ot×tanh(Ct)

(6)

其中所有的W和b均為參數，σ表示sigmoid激活函數，如式(7)所示。tanh表示雙曲正切激活函數，如式(8)所示。

(7)

(8)

1.2 LSTM預測方法

網絡流量預測是根據先前已知網絡流量數據預測未來網絡流量，它廣泛用于網絡規劃、資源管理和網絡安全中。Azzouni等[11]提出了一種基于LSTM的RNN框架，該框架可以有效地訓練用于大規模流量預測的網絡模型。訓練和比較各種參數的LSTM模型后發現LSTM模型可以快速收斂，并且可以為相對較小的模型提供更好的預測性能。通過真實網絡流量數據進行驗證，證明了LSTM模型性能優于傳統的線性方法，非常適合于網絡流量預測。但LSTM網絡本身對時間序列學習時存在早期特征記憶效果差、難以充分挖掘整個網絡流量特征等問題，為此進一步研究后，本文提出一種基于雙向長短期記憶循環神經網絡的網絡流量預測方法。

2 BiLSTM的網絡流量預測方法

基于LSTM的網絡流量預測方法在一定程度上提高了網絡流量預測的準確性，但該方法在對網絡流量進行學習時存在單一方向性等問題，忽略了網絡流量天與天之間雙向的聯系，難以充分利用整個網絡流量序列存在的特征。針對以上問題，為了能夠進一步提高網絡流量預測的準確性，本文提出一種基于雙向長短期記憶循環神經網絡的網絡流量預測方法。對網絡流量序列進行雙向的學習，避免單向學習導致較早學習部分特征提取和記憶效果差的問題。雙向學習可以充分挖掘網絡流量天與天之間雙向的聯系，完整地學習到網絡流量的整體特征。

2.1 BiLSTM網絡結構

BiLSTM神經網絡[15-16]是在LSTM神經網絡的基礎上改良而來的，由正向LSTM和反向LSTM神經網絡融合而成。BiLSTM同時考慮了序列過去的特征和未來的特征，使用兩個LSTM、一個正向輸入序列、一個反向輸入序列，再將兩者的輸出按照一定的權重結合起來作為最終的結果。BiLSTM[17-18]的隱藏層由正向LSTM細胞狀態和反向LSTM細胞狀態兩部分組成。流量序列通過輸入層進入隱藏層分別參與正向計算和反向計算，最終輸出結果由輸出層按照一定的權重融合正向LSTM輸出結果和反向LSTM輸出結果得到。BiLSTM的網絡結構如圖2所示。其中xt表示網絡的輸入，yt表示網絡的輸出。

圖2 BiLSTM網絡結構

2.2 BiLSTM預測方法

本文提出的基于BiLSTM的網絡流量預測方法繼承了LSTM預測方法的優點，同時彌補了LSTM預測方法的不足。BiLSTM預測模型如圖3所示。

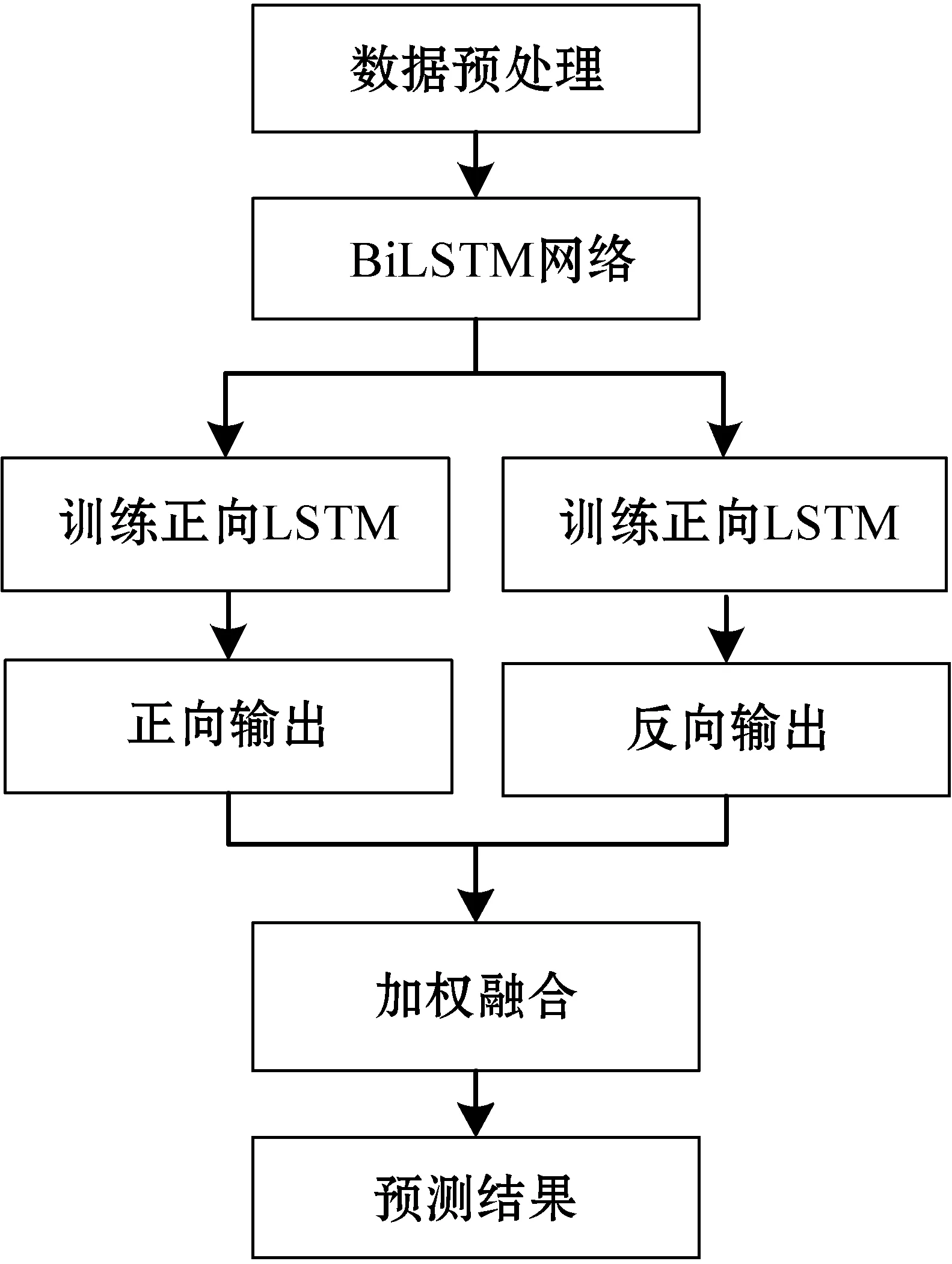
圖3 BiLSTM預測模型

基于BiLSTM的網絡流量預測算法分為訓練和預測兩個階段。

1) 訓練階段。BiLSTM預測模型訓練過程如圖4所示。

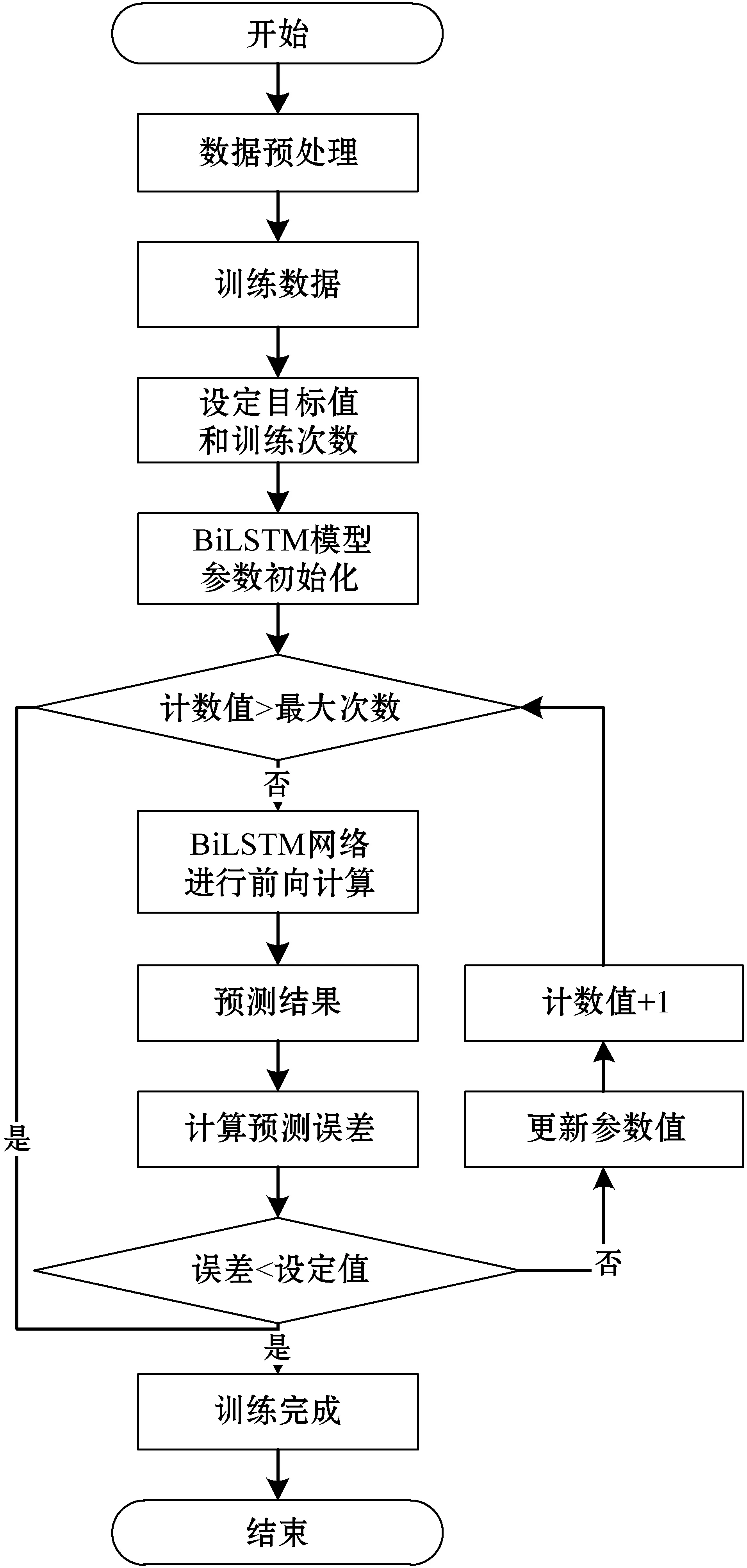
圖4 BiLSTM訓練流程

具體步驟如下：

步驟1利用滑動窗口技術對采集到的網絡流量原始數據進行處理，在數據歸一化后，進行數據劃分，得到網絡流量訓練集。

步驟2選定訓練樣本數，設定訓練目標值與最大訓練次數。

步驟3對BiLSTM網絡流量預測模型的各個參數進行初始化。

步驟4判斷訓練計數值是否大于設定的最大訓練次數，如果大于，執行步驟9，否則繼續往下，執行步驟5。

步驟5將訓練集的數據輸入到BiLSTM模型中，根據式(1)到式(6)進行前向計算。

步驟6BiLSTM的正向和反向LSTM網絡的輸出加權融合得到預測結果。

步驟7將預測結果與真實值進行比較，計算預測誤差值。

步驟8如果預測誤差值小于設定的目標誤差值，繼續執行步驟9。否則執行基于時間的反向傳播算法(Back Propagation Trough Time,BPTT)對網絡參數值進行更新，同時訓練計數值加1，返回步驟4。

步驟9完成對BiLSTM網絡的訓練。

2) 預測階段。流量預測過程如圖5所示。

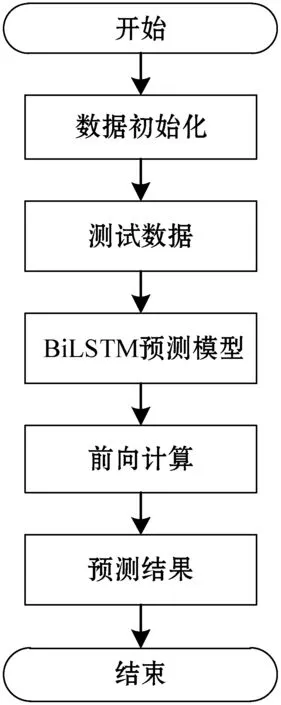
圖5 BiLSTM預測流程

詳細步驟如下：

步驟1利用滑動窗口技術對采集到的網絡流量原始數據進行處理，在數據歸一化后，進行數據劃分，得到網絡流量測試集。

步驟2將測試集的數據輸入到BiLSTM預測模型中，根據式(1)到式(6)分別進行前向計算。

步驟3BiLSTM網絡內部，正向和反向LSTM網絡的輸出加權融合得到預測結果。

3 仿真實驗

3.1 實驗數據與環境

網絡流量在1天和1星期內表現出較強的周期性和自相似性，利用該特性，選取1星期內的流量數據進行學習，對第8天的網絡流量進行預測，從而驗證提出方法的有效性。網絡流量在1 s和0.1 s不同時間尺度下表現出突發性，由于突發性是具有自相似性的網絡流量的一個明顯特征[19]，是長相關性引發的直接結果。長相關性是指：一個時間依賴的隨機過程，在非常大的時間范圍內或者在不同時間尺度下都表現出顯著的相關性。長相關性反映了自相似過程的持續現象，是自相似性的一個重要特征。所以對網絡流量進行分析，可以轉為研究網絡流量的自相似性。

本文所用的網絡流量原始數據集來自WIDE backbone數據庫，從該數據庫下載了2019年1月1日到1月8日連續8天，每天13時00分00秒到13時15分00秒的網絡流量原始數據。通過Wireshark網絡封包分析軟件，按照時間間隔1 s和0.1 s分別提取和統計每天的網絡流量數據，得到不同時間尺度下連續8天的網絡流量原始數據。網絡流量部分原始數據如圖6所示。將原始網絡流量數據輸入，利用滑動窗口方法進行截取處理。為了消除網絡流量指標之間的量綱影響，對網絡流量真實數據進行歸一化處理，以解決網絡流量數據指標之間的可比性。實驗所使用的電腦環境為Intel(R) Core(TM) i7-4790 CPU @3.60 GHz，16.00 GB RAM dell，MATLAB 2014a。

圖6 網絡流量原始數據

3.2 不同時間尺度下預測結果及分析

為測試本文提出的基于BiLSTM的網絡流量預測方法的真實有效性，經過大量實驗，選定BiLSTM網絡的參數為：輸入層神經元個數60，隱含層神經元個數100，輸出層神經元個數10，訓練5 000次，學習率0.001。分別對比BiLSTM和LSTM兩種方法在1 s和0.1 s不同時間尺度下，訓練集和測試集上的預測結果。兩種預測方法在一周連續7天，不同時間尺度數據集下，訓練集上的測試結果分別如圖7和圖8所示。

圖7 1 s時間尺度下訓練集上測試結果

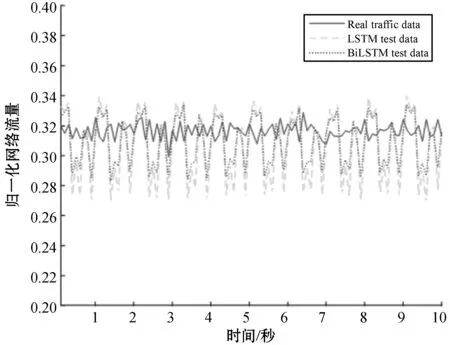
圖8 0.1 s時間尺度下訓練集上測試結果

從兩圖中可以看出，兩種預測方法在不同時間尺度的訓練集下，通過已知的前60步流量數據預測未知的后10步，BiLSTM預測方法由于在LSTM預測方法的基礎上引入了對網絡流量序列天與天之間進行雙向學習的思想，因此在訓練集上的測試結果相比LSTM預測方法的測試結果更加接近真實值。

圖9和圖10是時間尺度分別為1 s和0.1 s，兩種預測方法在測試集下的預測結果。從兩圖中可以看出，在不同時間尺度下，通過已知的前60步預測未知的后10步，BiLSTM預測方法繼承了LSTM預測方法的優點，同時彌補了LSTM預測方法的不足，因此在測試集上的預測結果更加收斂于真實流量數據。通過對兩種方法在不同時間尺度下，訓練集和測試集上預測結果的對比，驗證了本文所改進的網絡流量預測方法的有效性。

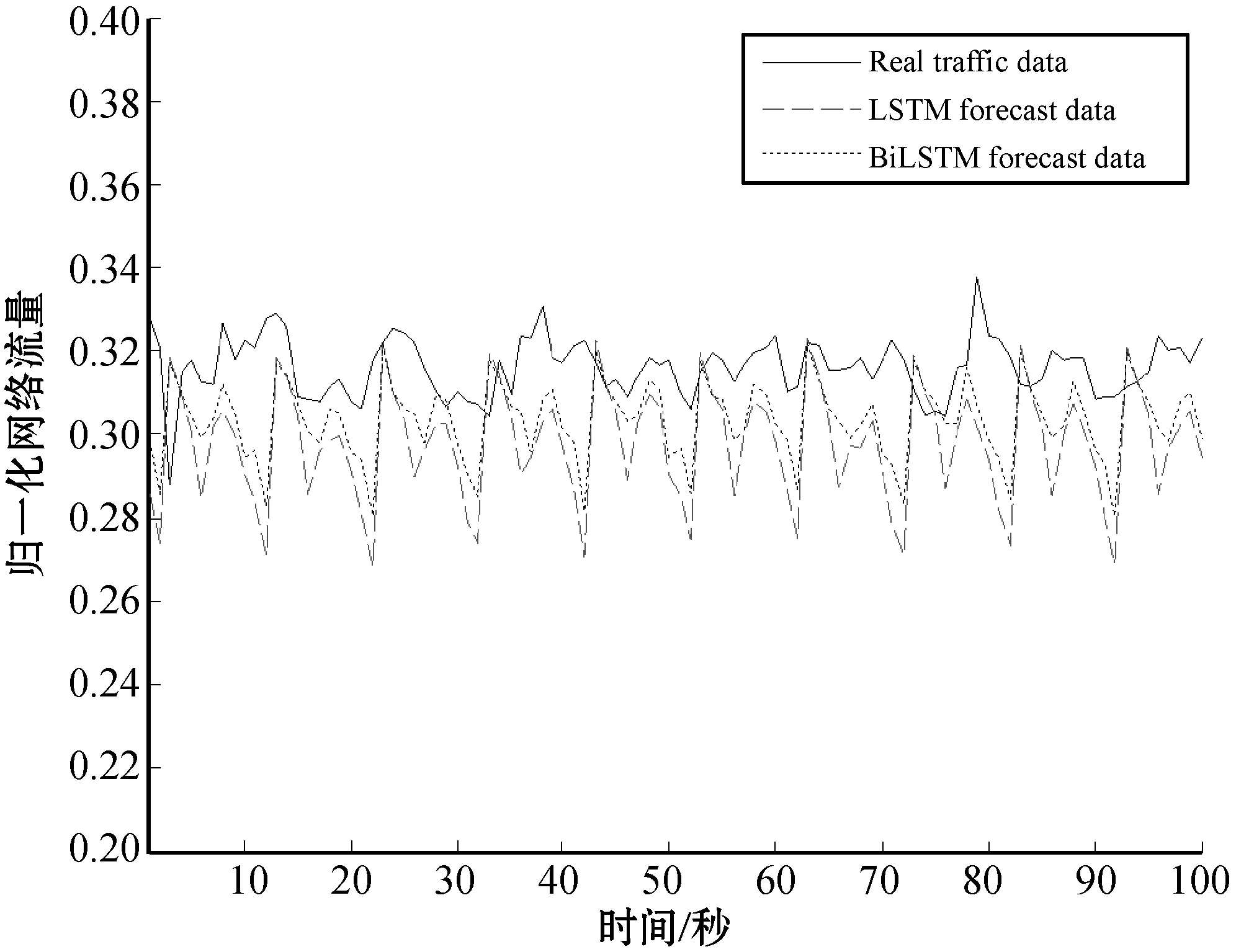
圖9 1 s時間尺度下預測結果

圖10 0.1 s時間尺度下預測結果

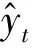
(9)

(10)

(11)

表1和表2分別表示了兩種網絡流量預測方法在1 s和0.1 s不同時間尺度下，在訓練集上分別進行大量測試實驗，將得到的預測結果與真實進行比較，計算后得到的多組實驗的平均相對誤差、平均絕對誤差和最小均方誤差的平均值。

表1 1 s時間尺度下網絡流量測試結果

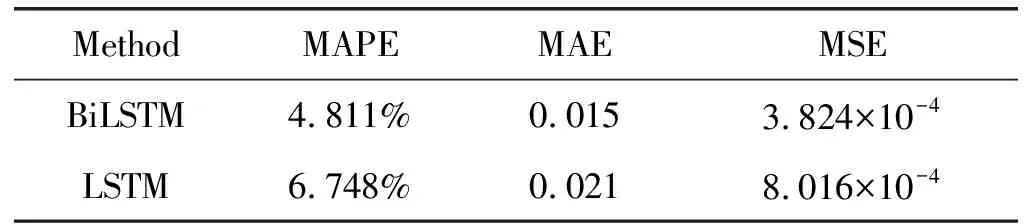
表2 0.1 s時間尺度下網絡流量測試結果

通過在不同時間尺度下，訓練集上測試結果的對比可以看出，BiLSTM預測方法由于在LSTM預測方法的基礎上引入了對網絡流量序列天與天之間進行雙向學習的思想，彌補了原方法存在的不足，最終預測結果的MAPE提高了0.491%，MAE和MSE相比原算法分別提高了22%和30%。

表3和表4分別表示了兩種網絡流量預測方法在1 s和0.1 s不同時間尺度下，在測試集上，分別進行大量預測實驗后，將得到的預測結果與真實值進行比較，計算后得到的多組實驗的MAPE、MAE和MSE的平均值。

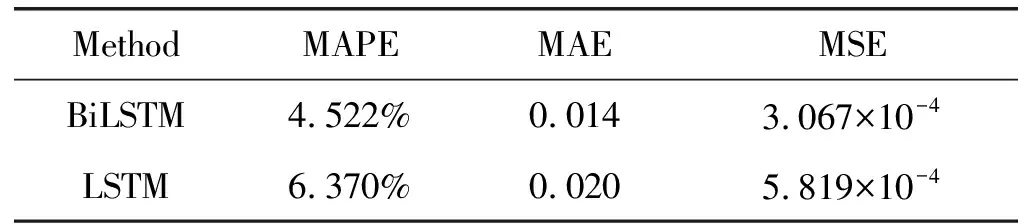
表3 1 s時間尺度下網絡流量預測結果

表4 0.1 s時間尺度下網絡流量預測結果

在不同時間尺度下，對比測試集上的預測結果可以看出，BiLSTM預測結果比LSTM預測結果的MAPE提高了1.848%，MAE和MSE相比原算法分別提高了30%和47%。通過兩種預測方法分別在1 s和0.1 s不同時間尺度下，訓練集和測試集上預測結果MAPE、MAE和MSE的對比，進一步驗證了本文提出基于BiLSTM的網絡流量預測方法是有效的，且預測效果優于基于LSTM的網絡流量預測方法。

4 結 語

本文針對基于LSTM的網絡流量預測方法存在學習單一方向性，越早學習部分特征記憶效果越差，難以充分利用整個網絡流量特征等問題，提出一種基于BiLSTM的網絡流量預測方法，對流量序列進行雙向學習，充分挖掘網絡流量的整體特征。采用真實網絡流量數據庫，對1 s和0.1 s不同時間尺度下的網絡流量進行預測，分析結果表明：改進后的方法相比原方法具有更好的預測精度，MAPE提高了1.848%。