碳稅機制下的生鮮農產品冷鏈配送路徑優化研究

安璐，寧濤，宋旭東，王佳玉

(1. 大連交通大學 計算機與通信工程學院, 遼寧 大連 116021；2. 大連民族大學 計算機科學與工程學院，遼寧 大連 116000)①

全球碳排放統計中交通運輸碳排放占14%，道路碳排放占交通運輸碳排放70%[1-2].冷鏈物流配送有高能耗和高碳排放特點.因此，如何優化冷鏈物流配送路徑降低碳排放量和運輸成本是十分重要的.車輛路徑問題(VRP)最早是由Dantzig在1959年提出的[3]，在此基礎上，Solomon[4]認為車輛配送需考慮時間花銷帶來的影響，Jabali[5]考慮軟時間窗建立VRP模型.涂海寧[6]考慮物流配送準時化需求建立車輛配送模型,夏揚坤[7]考慮工作時間和軟時間窗建立雙目標車輛路徑模型.Franceshette[8]、Xiao[9]、Wen[10]將車輛出發時間、車輛速度、容量進行綜合考慮，分別用三種不同的算法對模型進行求解.范厚明[11-12]考慮模糊需求和模糊時間窗構建多目標優化模型.康凱[13]考慮制冷成本和運輸過程中產生的碳排放量建立模型，李順勇[14]分析交通擁堵帶來的影響，提出多通路時變網絡低碳車輛路徑模型.寧濤[15-18]提出干擾管理物流配送模型，實驗結果說明所提出的方法有效降低了干擾事件對成本的影響.方文婷[19]考慮碳排放綜合成本建立多目標優化模型，同時，趙志學[20]考慮交通擁堵狀況建立冷鏈物流配送模型，饒衛振[21]提出低碳協作車輛路徑問題模型.馬秋卓[22]建立城市配送最優VRP模型，驗證容量變化對于綜合成本、碳排放量的影響.饒衛振[23]考慮道路坡度變化對碳排放的影響建立低碳配送模型.陳志[24]考慮不同配送時間和行駛路段對碳排放的影響建立低碳車輛配送模型進行求解.

綜上所述，許多學者在低碳配送問題上的不同方向進行了深入的研究，但存在有限性.主要體現如下：①現有模型只考慮配送距離、容載量和時間花銷對碳排放的影響，較少引入碳稅機制；②已有文獻對于制冷設備的卸貨時間和不同需求時間的運輸成本對碳排放量的影響考慮較少.因此，本文考慮卸貨時間和不同需求時間對碳排放的影響，引入碳稅機制，建立數學模型，并將碳稅成本作為算法的決策變量，提出改進的量子蟻群算法求解模型.

1 低碳配送路徑優化問題數學模型

1.1 冷鏈物流配送模型建立

構建冷鏈物流配送路徑優化問題模型為：

(1)

其對應約束條件為：

(2)

(3)

(4)

(5)

(6)

tj=ti+tij

(7)

式(2)限定運輸車輛在運輸過程中不能超過最大容載量；式(3)限定每個客戶點只能被一輛運輸車輛服務；式(4)和(5)限定對于任意客戶只允許車輛出發和到達一次；式(6)消除子回路條件；式(7)限定配送過程中車輛的運輸是連續的.

1.2 冷鏈物流配送成本分析

在式(1)中，Z1表示車輛綜合運輸成本，由車輛固定成本和車輛運輸成本構成，則Z1如式(8)：

(8)

考慮產品消耗對于運輸制冷和卸貨制冷成本影響，引入碳稅系數ω，分析碳排放量，Z2表示碳稅成本：

(9)

考慮車輛容載量，燃油消耗和運輸距離的線性關系作為計算運輸過程中碳排放成本的工具[25].ρ0為容載量為0時單位距離油耗，ρ*為容載量最大時單位距離油耗.則在車輛容載量為Qij時，客戶節點(i,j)碳排放成本FCij為：

(10)

引入生鮮農產品新鮮度衰減函數定量分析貨物損耗情況[26].?1為運輸制冷過程的產品新鮮衰減系數，?2為卸貨制冷過程的產品新鮮衰減系數，且?1

(11)

(12)

考慮客戶時間需求窗(Ej,Lj),將ε1為早到客戶點時間懲罰系數.ε2為晚到客戶點的時間懲罰系數，時間懲罰成本Z3為：

(13)

2 改進量子蟻群算法設計及應用

2.1 量子信息素編碼

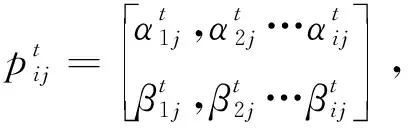
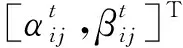
(14)

(15)

式(15)中，

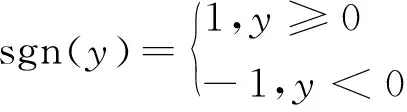
φ0為最初的量子旋轉角度，設定為0.05π. sgn(αij,βij)為旋轉角可調整的方向，sign(f(Z2)-f(bi))使φi根據建立的碳稅成本與當前α和β的值進行自適應調整.f(Z2)為當前所求得的碳稅成本，f(bi)為當前所求得的最優碳稅成本.

2.2 狀態轉移規則

考慮客戶點需求時間窗(Ej,Lj)和卸貨時間，改進后第k條路徑上的螞蟻狀態選擇規則為：

(16)

式(16)中，allowedk表示可被服務的客戶點的集合，其中v0為運輸中心；θ1為概率選擇權重系數，θ2為時間約束權重系數，滿足0≤θ1，θ2≤1，并且θ1+θ2=1；α表示信息素的影響度，β表示信息素能見度的影響度.ηij為信息素的可見度；μj為客戶點j的量子信息素可見度，γ為量子比特的啟發因子.

2.3 信息素的更新

螞蟻尋優過程中，之前路徑上的量子信息素會不斷地揮發，而最優螞蟻在走過的路徑上會釋放新的量子信息素，信息素更新策略為：

(17)

(18)

式(18)中σ為每代中最小碳稅成本螞蟻的個數，Q*表示信息素濃度總量.

2.4 算法應用

改進量子蟻群算法的算法步驟為：

步驟1：初始化參數.初始化量子螞蟻種群數N，共有m個量子位.初始化α、β、ρ、θ1、θ2和信息素總量Q，設置NC=0，將客戶點放置于當前解集中；

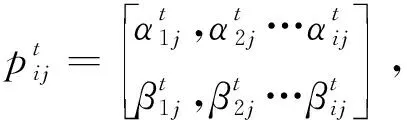
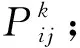
步驟4：計算目標函數值.當所有客戶點都加入解集后，計算目標函數值z和Z2，并記錄保留當前的最優解，將所有螞蟻返回運輸中心；

步驟5：自適應量子旋轉角調整.依據計算的碳稅成本Z2和當前概率福αij和βij自適應調整量子旋轉角；

步驟6：更新信息素.依據計算的碳稅成本Z2和調整過后的|βij|2對各邊的量子信息素更新；

步驟7：輸出目標函數值.判斷是否達到NCmax，若達到，則輸出最優目標函數值；若沒有達到，轉步驟3.

3 實例求解與分析

本文選取文獻中物流配送的13個超市門店作為服務點，并根據文獻中實際配送數據作為實驗參數[11].運輸中心編號為0，各個超市客戶點的編號為1,2,3……12,13.超市客戶點的詳細需求信息如表1所示.

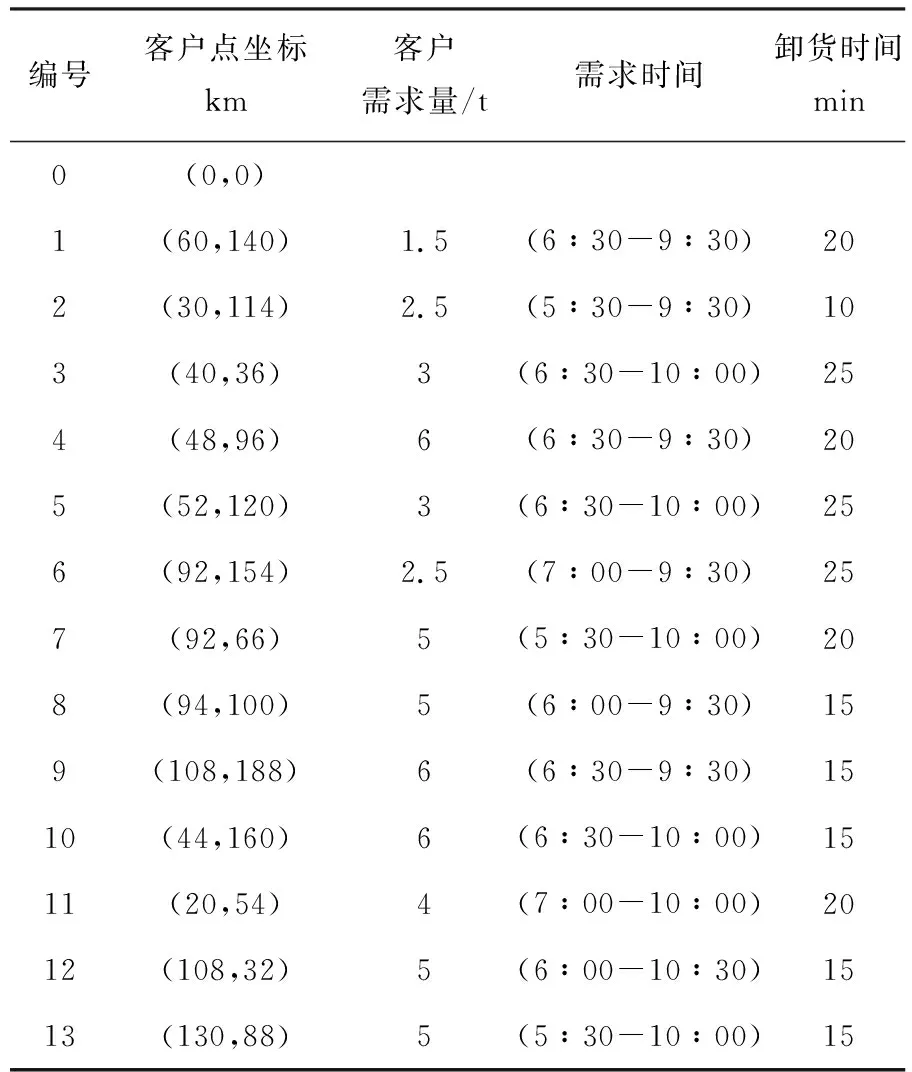
表1 超市客戶點詳細需求信息表

3.1 碳稅成本對比及分析

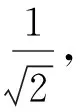
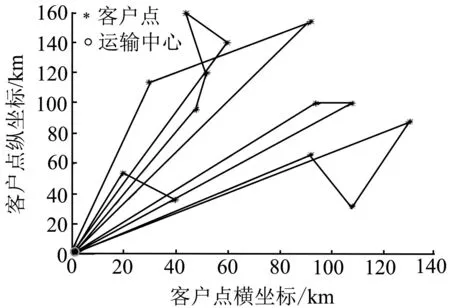
(a) 碳稅成本最低路徑圖

碳稅成本最低的運輸策略為：從運輸中心出發5輛車，路線依次為：0-1-10-5-4-0; 0-7-12-13-0; 0-11-3-0; 0-9-8-0; 0-2-6-0.此策略下的最短路徑為1 989 km,綜合成本為4 393元，碳稅成本為3 978元.

配送路徑最短的運輸策略為：從運輸中心出發4輛車，路線依次為：0-1-10-5-4-0; 0-2-11-3-0; 0-6-8-9-0; 0-13-7-12-0.此策略下的最短路徑為1 879 km,綜合成本為4 459元，碳稅成本為4 163元.

由表2分析可知，配送路徑最短并不一定可以使碳稅成本和綜合成本降低.實驗結果表明，雖然在考慮碳稅模型下的配送路徑約增加0.5%，但相比之下綜合成本下降1%，碳稅成本下降4%，驗證了該模型的有效性.

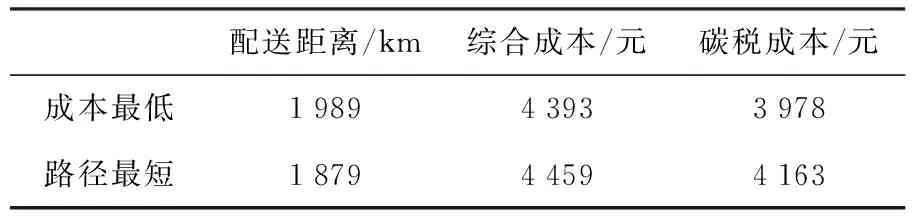
表2 考慮碳稅成本最低和配送路徑最短的結果對比

3.2 局部優化及穩定性分析

采用上述實驗參數，分別對初始化信息素不同情況進行對比分析，將算法隨機進行10次后進行對比，實驗結果如表3所示.

表3 初始化信息素對比結果

由表3實驗結果可知，通過對改進量子蟻群算法初始化量子信息素后，在算法尋優74代后找到目標函數的最優值，并通過所提出的自適應量子旋轉角調整策略更新信息素，加快了算法的收斂速度，降低了冷鏈物流配送的綜合成本和碳稅成本，進一步驗證該算法的有效性.

3.3 不同算法對比

進一步驗證算法的有效性，選擇上述實驗參數，對提出的改進量子蟻群算法與基本量子蟻群算法[18]和蟻群算法[19]進行對比.實驗隨機進行了10次，對比結果如圖2所示.

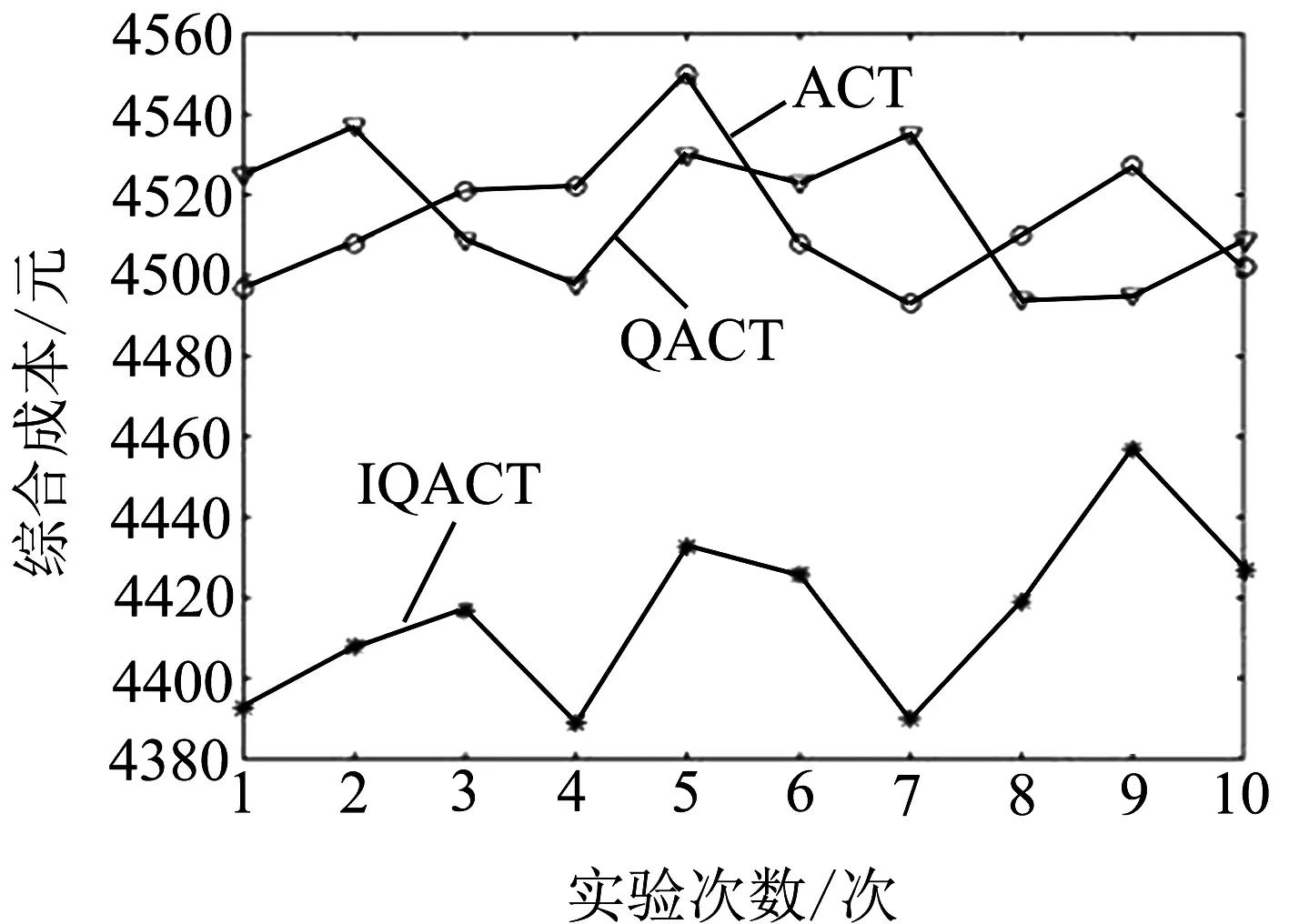
(a) 綜合成本對比結果圖

由圖2實驗結果可以得出，本文所提出的算法實驗結果與基本蟻群算法相比，最小綜合成本約減少3%，碳稅成本約減少6%；與基本量子遺傳算法相比，最小綜合成本約減少2.3%，碳稅成本約減少4.3%.

4 結論

本文針對碳稅機制下的生鮮農產品冷鏈物流配送進行研究.主要成果如下：

(1)考慮碳稅成本，通過對配送路徑最短和配送成本最小兩種情況進行對比分析.實驗結果表明，配送路徑最短并不能有效降低碳稅成本和綜合成本;

(2)局部優化分析.所提出的量子編碼初始化信息素增加了種群選擇的空間，所提出的自適應量子旋轉角調整策略加快了算法的收斂速度，解決了局部最優的困擾，降低了運輸過程中的碳稅成本和綜合成本;

(3)算法對比.實驗結果表明，本文所提出的算法可以有效降低運輸過程中的碳稅成本和綜合成本，進一步說明了本文提出的模型和算法是有效的.

在此基礎上，如何減少不確定干擾事件(如交通堵塞等)對成本的影響是本文下一步研究的方向.