筒倉中小麥密度分布值的有限元分析

王 穎， 程緒鐸， 唐福元

(南京財經大學食品科學與工程學院；江蘇省現代糧食流通與安全協同創新中心，南京 210046)

我國是全球第一大小麥生產國。2019年我國小麥產量1.33億t，消費量為1.28億t[1]。小麥儲藏在糧倉中，自身的重力與摩擦力、倉壁對小麥的壓力與摩擦力引起了小麥塊的變形與壓縮[2,3]，導致小麥孔隙率減小、堆密度增大。Thompson等[2]研究發現小麥堆密度隨著內部的壓力變化而變化。小麥儲藏在筒倉中，小麥堆的壓應力分布是不均勻的，尤其是壓應力隨著糧層深度的增加而增加，因此筒倉中小麥堆的密度分布也是不均勻的，也是隨著糧層深度的增加而增加。確定筒倉中小麥堆的密度分布值是準確計算筒倉中的糧食質量的關鍵參數，也是預測筒倉小麥堆通風阻力、小麥堆濕熱傳遞規律的重要參數[4,5]。

通常用氣體密度儀來測量糧堆的堆密度[6-9]。氣體密度儀測量的只是小糧堆的堆密度(糧堆體積小于10 L)且測定的是無壓縮的糧食密度，它無法被送達到糧堆深處，因此不能用來測量筒倉深處的糧食堆密度。我國一般使用容重儀測定糧食的密度，但測定的是無壓縮的糧食密度，同樣無法測定筒倉深處受壓縮的糧食密度。Cheng等[10]建立筒倉內小麥分層壓縮平衡方程，數值求解了筒倉中小麥各層的堆密度。這個分層壓縮平衡方程是筒倉中各層小麥堆密度的平均值，不是某一糧層上各糧塊的堆密度。

ABAQUS是國際上功能最強的大型通用有限元軟件之一，擁有能夠真實反映松軟土體的修正劍橋模型，已應用于研究土體中的力學問題。小麥堆的力學特性與松軟土體相似，本研究使用ABAQUS軟件求解筒倉中的小麥堆的修正劍橋模型。通過有限元方法求解筒倉中的小麥堆的修正劍橋模型得到筒倉中小麥堆密度的三維空間分布值，即小麥堆密度隨糧塊深度(縱向)、徑向、環向變化的分布值。

1 材料與方法

1.1 實驗材料

小麥，煙農19號，產自江蘇淮陰，人工剔除實驗樣品中破損籽粒和雜質，測得原始含水率為12.66%。實驗樣品的含水率分別調制為10.60%、12.66%、14.22%、16.13%。調制好含水率的樣品裝在塑料袋中封閉好，然后儲藏在人工氣候箱中，人工氣候箱中的溫度設置為4 ℃。實驗前從人工氣候箱中取出小麥樣品，采用標準烘箱干燥法在130 ℃下干燥實驗樣品19 h測定它的含水率(ASAE Standards, 2001)，重復3次。

1.2 小麥堆應力與應變關系模型

儲藏在筒倉中的小麥堆在外力作用下產生應力，而應力的作用又引起應變。要求解筒倉中小麥堆的應力分布與應變分布必須建立小麥堆應力與應變關系模型。修正劍橋模型將總應變分為剪切應變與體積應變，總應力分為平均正應力與剪切應力，適合求解筒倉中小麥堆的體積應變(應變較大)。故本研究選擇修正劍橋模型來表征小麥堆的應力與應變關系。

修正劍橋模型中的應變增量包括體積應變增量dεv和剪切應變增量dεs；應力增量為平均正應力增量dp和剪切應力增量dq，q=σ1-σ3是廣義剪切應力，p=(σ1+2σ3)/3是平均主應力。

修正劍橋模型的彈塑性矩陣的顯式表達式為[11]：

(1)

Cpp=

(2)

Cpq=Cqp=

(3)

Cqq=

(4)

由式(2)～式(4)可見，修正劍橋模型有6個參數：e為初始孔隙比，ν為泊松比，E為彈性模量/kPa，M為臨界狀態應力比，κ為等向膨脹指數，λ為對數硬化模量；這6個參數可以通過三軸壓縮與剪切實驗而確定[11]。

1.3 修正劍橋模型參數的確定

1.3.1 初始孔隙比的確定

1.3.1.1 初始孔隙率ε的測定

小麥初始孔隙率ε是未壓縮時小麥堆中孔隙體積與小麥堆體積之比，測定初始孔隙率是為了得到初始孔隙比。本研究使用LKY-1型糧食孔隙率測定儀(見圖1)測定小麥的初始孔隙率。

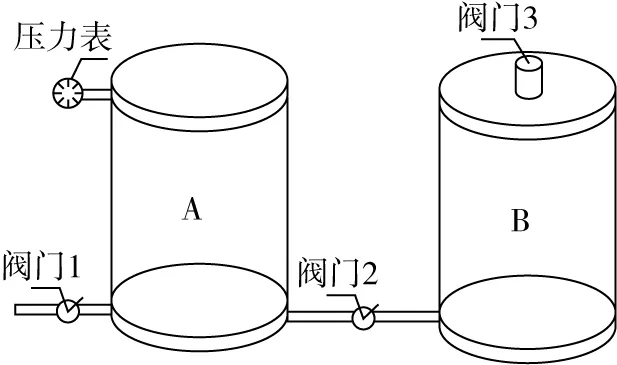
圖1 孔隙率測定儀示意圖

如圖1所示，兩個容積相等的壓力容器A和B，在容器B中裝滿樣品并將其密封。關閉閥門2，打開閥門1、3，用空氣壓縮機向容器A中鼓入一定壓力的氣體。當壓力表指針達到一定數值時，關閉閥門1，當壓力值穩定后，記下壓力表讀數P1；關閉閥門3，然后打開閥門2，當容器A和B中壓力平衡時，記下此時壓力表讀數P2。視空氣為理想氣體(標準大氣壓為Pa)，由理想氣體等溫過程的特性推出小麥初始孔隙率(未壓縮)為：

(5)

1.3.1.2 初始孔隙比e的確定

初始孔隙比e指未壓縮時小麥堆中孔隙體積與小麥堆中籽粒體積之比，小麥樣品初始孔隙比(未壓縮)可由初始孔隙率推導得到:

e=ε/(1-ε)

(6)

1.3.2 臨界狀態應力比M的測定

對樣品進行軸向壓縮實驗[12]測定臨界狀態應力比M。在軸向壓縮實驗中，選定5個圍壓σ3：30、50、70、90、110 kPa。裝好樣品后，啟動儀器對樣品進行剪切(剪切應變速率為1.000 mm/min)，位移每增加0.4 mm，記錄1次測力計讀數和樣品體積減少量，直至測力計讀數出現最大值時，記下峰值時平均主應力p和廣義剪切力q。對每個圍壓，實驗重復3次。將這5組實驗的破壞點(即最大主應力差)所對應p和q繪制在p-q平面中，經一元線性回歸得直線的斜率M值。

1.3.3 對數硬化模量λ和等向膨脹指數κ的測定

對數硬化模量λ和等向膨脹指數κ的測定實驗為各向等壓實驗[12]，使圍壓σ3從0 kPa增加至200 kPa，圍壓每增加5 kPa，記錄1次樣品體積減少量，待圍壓增至200 kPa，再依次卸載至0 kPa，同樣每減小5 kPa，記錄1次樣品體積增加量。將加載曲線和卸載曲線上的p和所對應的孔隙比e繪制在e-lnp平面中，經一元線性回歸得直線的斜率λ和κ值。

1.3.4 彈性模量E和泊松比υ的測定

選定圍壓σ3分別為30、50、70、90、110 kPa，對樣品進行軸向加卸載循環的常規三軸壓縮實驗[12]，測定彈性模量E。在常規三軸壓縮實驗中，糧堆樣品呈圓柱形，軸向壓力為σ1，圍壓為σ3，主應力差為Δσ=σ1-σ3，當主應力差達到最大值時糧堆破壞。對于每一個圍壓σ3，可測定一個最大主應力差。對選定的圍壓σ3，分級施加軸向壓力，每級壓力取試樣最大主應力差的10%；施加第1級壓力，并開動秒表，記錄加壓1 min后位移計的讀數，每1 min施加一級壓力，記錄位移計讀數，直至施加到第4級壓力為止；在施加第4級壓力1 min后記錄位移計的讀數，并逐級卸壓，每1 min卸去1級壓力，并記錄卸壓后1 min時位移計的讀數，直至卸去所有施加的軸向壓力；重復加卸載荷4次。

彈性模量E按第4次加卸載荷記錄的數據計算公式為：

(7)

式中：Δhe為小麥樣品的軸向彈性變形量/mm；hc為未軸向加載時小麥樣品高度/mm。

如同測定等向膨脹指數κ一樣，對小麥樣品進行各向等壓實驗，體變彈性模量K按卸載記錄的數據計算公式為：

(8)

式中：ΔV為小麥的彈性體積增量/m3；V為未加壓力時小麥樣品的體積/m3。

泊松比ν按公式計算：

(9)

1.4 筒倉中小麥堆密度分布的有限元求解方法

1.4.1 筒倉的幾何尺寸與力學參數

筒倉的幾何尺寸與力學參數見表1。

表1 筒倉幾何尺寸及其材料的參數

1.4.2 筒倉與小麥堆單元網格劃分

筒倉高31 m, 重力未施加時筒倉內小麥堆高度29 m。筒倉與小麥堆的形狀和受力都是軸對稱的，取筒倉與小麥堆的一徑向平面表示筒倉與小麥堆，選擇四邊形單元劃分該徑向平面，四邊形單元的面積為1×1=1 m2,每一個四邊形單元代表一個截面為矩形的環形體。小麥堆模塊被劃分為29×5個單元；倉壁模塊被劃分成31×1個單元。

1.4.3 小麥堆與筒倉壁的接觸模擬

倉壁內側面與小麥堆外側面有相互力的作用。接觸面之間傳遞切向應力與法向應力，切向應力即摩擦力。在有限元分析中應考慮阻止兩表面之間相對滑動而產生的摩擦力。庫侖模型是常用的摩擦模型，通過摩擦系數來描述兩表面間的摩擦行為。臨界剪應力與法向接觸壓力之間的關系為：

τ=μp

(10)

式中：μ為摩擦系數；p為法向接觸壓力/kPa。

1.4.4 載荷及邊界約束

筒倉中小麥堆受到自重、內摩擦、倉壁對小麥的抵抗等多種力的作用，小麥堆的重力由體積力進行描述，體積力是主動力。小麥堆內部作用力通過小麥堆的應力與應變的本構關系進行描述，小麥堆與倉壁之間的相互作用力由摩擦力與正壓力進行描述。將小麥堆模型底部邊界條件設置為U2=0，即對筒倉底板處節點豎直方向的位移約束。因為在儲藏過程中，筒倉是不產生任何運動的，故將倉壁處節點位移完全約束，以限制其剛體位移。

1.4.5 筒倉中小麥堆各處密度的計算

小麥堆共有n×m個單元，n(29)為行數，m(5)為列數。重力未施加時各單元密度是相同的；重力加載后，每個單元在筒倉中的位置及其體積都發生了變化。若i表示行(縱向)編號，j表示列(橫向)編號，則第i行j列的單元的密度可由公式計算：

(11)

2 結果與分析

2.1 初始堆密度(未壓縮)

根據國家標準GB/T 5498—1985測定得到含水率分別為10.60%、12.66%、14.22%、16.13%的煙農19號表層密度(未壓縮)分別為801.75、787.09、770.47、755.65 kg/m3。

2.2 修正劍橋模型參數

使用應變式三軸儀和糧食孔隙測定儀測定煙農19號的修正劍橋模型參數參數如表2所示。

表2 修正劍橋模型參數

2.3 筒倉中小麥堆的密度分布值

根據國家標準GB/T 5498—1985測定得到含水率分別為10.60%、12.66%、14.22%、16.13%的小麥堆(煙農19號)初始密度(表層密度)分別為801.75、787.09、770.47、755.65 kg/m3。使用修正劍橋模型和有限元軟件ABAQUS計算得到筒倉中小麥堆的密度分布值，見圖2。

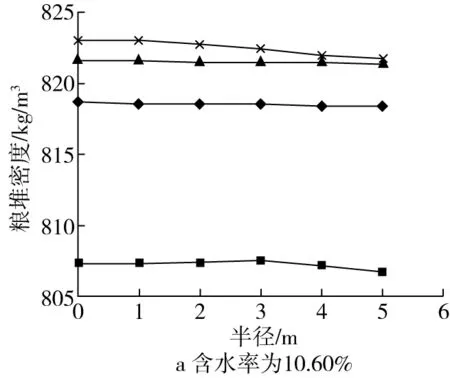
圖2 不同含水率小麥堆的密度與半徑的關系

由圖2可知，筒倉中小麥堆的密度隨著糧層深度的增加而逐漸增大，而在筒倉拐角處的小麥堆密度隨著糧層深度的增加而逐漸減小。在上部糧層，隨著糧塊與筒倉中心軸距離的增加，密度緩慢減小，減小值約為0.07%～0.1%。在中部糧層，隨著糧塊與筒倉中心軸距離的增加，密度幾乎不變。在接近倉底層，隨著糧塊與筒倉中心軸距離的增加，密度逐漸減小，減小值約為0.4%～0.6%。

2.4 筒倉中小麥堆平均密度與糧層深度的關系

重力未施加時筒倉內小麥堆高度29 m。筒倉與小麥堆的形狀和受力都是軸對稱的，取筒倉與小麥堆的一徑向平面表示筒倉與小麥堆，選擇四邊形單元劃分該徑向平面，四邊形單元的面積為1 m2,每一個四邊形單元代表一個截面為矩形的環形體。小麥堆模塊被劃分為29×5個單元；倉壁模塊被劃分成31×1個單元。這樣小麥堆共有29行5列。筒倉中小麥堆第n層(行)平均密度按式(12)計算：

(12)

依據修正劍橋模型計算的數據，由式(12)計算得到小麥堆各糧層的平均密度，如圖3所示。在小麥含水率為10.60%、12.66%、14.22%、16.13%時，小麥堆的糧層深度的變化范圍分別為0～27.704 8、0～27.661 0、0～27.485 8、0～26.982 1 m；其平均密度的變化范圍分別為800.75～822.08、786.02～807.61、769.32～792.69、754.33～783.23 kg/m3。在同一含水率下，小麥堆的糧層平均密度隨著糧層深度的增大而逐漸增大，逐漸趨于恒定值。

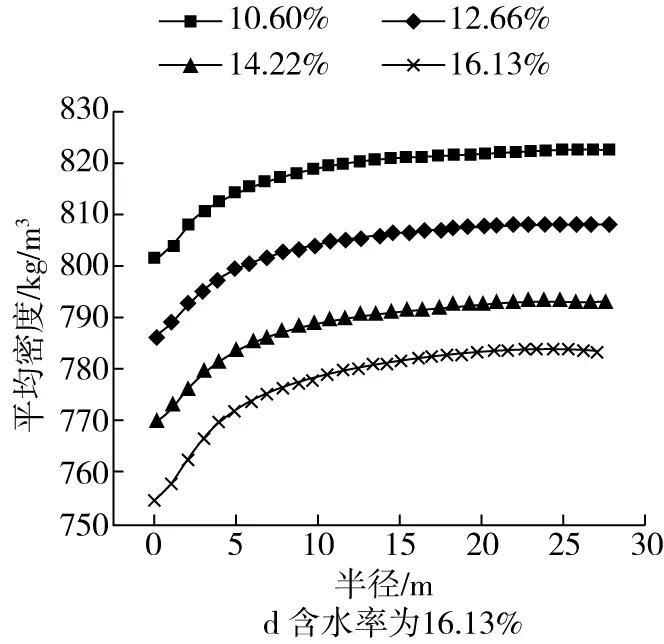
圖3 不同含水率下小麥堆的平均密度與糧層深度的關系

2.5 筒倉中小麥堆平均密度與含水率的關系

從圖3可以看出，含水率為10.60%、12.66%、14.22%、16.13%的小麥堆在相同的糧層深度下的平均密度是隨著含水率的增大而減小的。

2.6 筒倉中小麥堆平均密度與含水率、糧層深度關系模型

有限元計算的密度數據有這樣的規律，當深度一定時密度與含水率大致成線性關系，當含水率一定時密度隨深度增加而增大，增加率隨深度增加而減小，故用1-eah3+bh2+ch表達密度隨深度增加的變化趨勢。因此，設小麥糧層平均密度與糧層深度、含水率的關系方程為：

ρ=ρ0+(ρmax-ρ0)(1-eah3+bh2+ch)

(13)

式中：ρ為小麥堆糧層平均密度/kg/m3；ρ0為小麥堆初始密度/kg/m3；ρmax為小麥堆壓縮糧層平均密度的最大值/kg/m3；h為小麥堆糧層深度/m。

表3 入倉小麥的參數

小麥堆初始密度與含水率的關系可擬合為線性方程(14)。

ρ0=892.35-8.56MCρ=0.99

(14)

式中：MC為小麥堆含水率/%。

通過式(12)計算得到的小麥堆糧層平均密度的最大值變化范圍為822.08～783.33 kg/m3，其隨含水率的增大而降低。小麥堆糧層平均密度的最大值與含水率的關系可擬合為線性方程(15)。

ρ0=897.99-7.20 MCR2=0.99

(15)

為了確定模型(13)中a、b、c這3個模型常數，將式(13)變換成式(16)：

(16)

以ln(1-(ρ-ρ0)/(ρmax-ρ0))為縱坐標，h為橫坐標，按式(16)進行數據擬合從而得到模型常數a、b、c分別是-0.000 47、0.012、-0.24。

將a、b、c的值及式(14)和(15)代入式(13)，可得小麥堆糧層的平均密度與含水率、糧層深度的關系模型為：

ρ=892.35-8.56MC+(5.64+1.36MC)(1-e-0.000 47h3+0.012h2-0.24h)

(17)

圖3中的散點是有限元方法計算的密度，曲線表示模型方程(17)計算的密度值。由圖3可以看出，經模型方程(17)計算得到的小麥堆糧層密度與限元方法計算的糧層密度誤差較小，對于含水率分別為10.60%、12.66%、14.22%、16.13%的小麥，模型方程(17)計算的小麥堆糧層平均密度與有限元方法計算的糧層平均層密度的誤差小于0.5%，說明模型方程(17)有效。

2.7 實倉驗證

實例一：中央儲備糧溫州直屬庫11、12、13、14號筒倉內徑為10 m，入倉小麥的參數見表3。本研究通過有限元分析方法求解修正劍橋模型計算得到小麥的糧層密度分布值，再由積分方程計算出儲糧總質量，并與筒倉中實際儲糧質量進行比較，結果見表4。

表4 修正劍橋模型計算結果與實際儲糧數量的比較

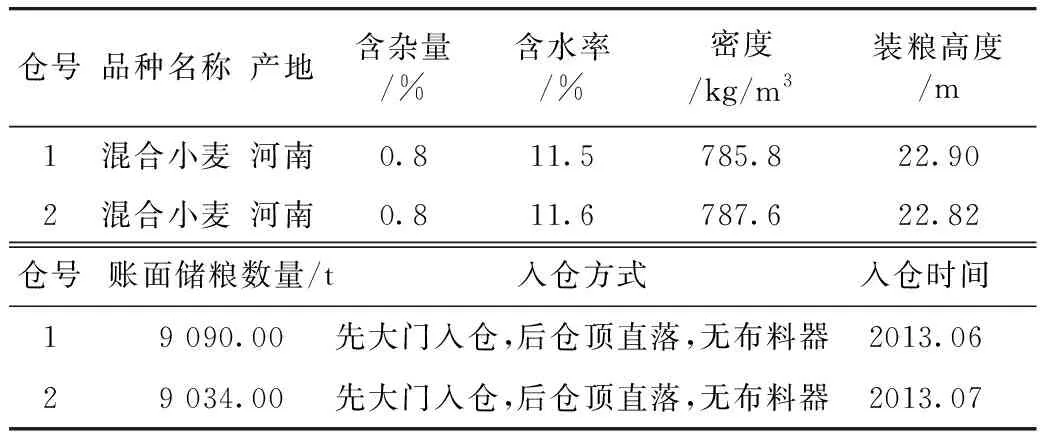
表5 入倉小麥的參數

實例二：中央儲備糧金華直屬庫1、2號淺圓倉內徑為25 m，入倉小麥的參數見表5。本研究通過有限元分析方法求解修正劍橋模型計算得到小麥的糧層密度分布值，再由積分方程計算出儲糧總質量，并與筒倉中實際儲糧質量進行比較，結果見表6。

表6 修正劍橋模型計算結果與實際儲糧數量的比較

由表4與表6可以看出，本研究的修正劍橋模型計算結果與實際賬面數誤差小于0.3%，說明本研究的修正劍橋模型計算的密度分布值可靠性較高。

入倉方式對糧食分級有影響，糧食分級對密度的分布有影響，糧食入倉以后，由于糧食分級，同一層的糧食密度差別增大，但一層的平均密度變化很小，所以對計算糧食總質量影響較小，本研究的模型計算結果表明影響較小。糧食含雜量對壓縮密度有影響，本研究選擇的實倉中的小麥含雜量較小(0.2%～1.0%)，所以對計算糧食總質量影響較小，本研究的模型計算結果表明影響較小。

3 結論

筒倉中小麥堆的密度隨著糧層深度的增加而逐漸增大，而在筒倉拐角處的小麥堆密度隨著糧層深度的增加而逐漸減小。在上部糧層，糧塊密度隨著糧塊與筒倉中心軸距離的增加而緩慢減小，減小值為0.07%～0.10%。在中部糧層，糧塊密度隨著糧塊與筒倉中心軸距離的增加幾乎不變。在接近倉底糧層，糧塊密度隨著糧塊與筒倉中心軸距離的增加而逐漸減小，減小值為0.4%～0.6%。小麥堆的糧層平均密度隨著糧層深度的增大而逐漸增大，逐漸趨于恒定值。相同深度下的糧層平均密度隨著含水率的增大而減小。筒倉中小麥堆糧層平均密度與含水率、糧層深度之間關系方程為：ρ=892.35-8.56MC+(5.64+1.36MC)(1-e-0.000 47h3+0.012h2-0.24h)。實倉驗證得到，由修正劍橋模型計算的筒倉中小麥的總質量與實際糧倉的賬面小麥總質量誤差小，相對誤差在0.14%～1.25%之間。