波浪錐型圓柱流固耦合振動機理研究

鄒 琳， 秦 傲， 楊耀宗， 列煜俊， 徐勁力

(武漢理工大學 機電工程學院， 武漢 430070)

圓柱繞流渦激振動一直是工程領域廣泛關注的熱點，之前學者的研究主要集中在探究圓柱繞流渦激振動機理及如何將圓柱的鎖頻區間變窄，抑制渦激振動的發生[1-2]。周國成等[3]探究了不同剛度系數對二維圓柱渦激振動的影響。Bahmani等[4]發現系統質量比或阻尼比降低會導致振幅和鎖頻區間增加，圓柱下游出現“2S”模式的渦旋脫落(以下簡稱渦脫)，與Williamson等[5]的研究結果相一致。鄒琳等[6]對不同間距比的二維串列雙圓柱進行了渦激振動響應特性研究，研究了在雙自由度條件下下游圓柱的鎖頻區間、振動頻率等特性。康莊等[7]研究了低質量比條件下，雷諾數對圓柱渦激振動的影響規律。唐友剛等[8]發現順流向振動會對橫流向振動產生影響，且順流向振動的振幅也會增大。陳威霖等[9]研究發現圓柱串列排列時，由于圓柱之間的耦合作用，圓柱會出現不同類型的渦激振動響應，流體力也呈現不同的變化。Zhang等[10]在雷諾數Re=5 000時對波浪型圓柱渦激振動與固定繞流進行比較，發現在零結構阻尼的情況下，波浪形狀表面對減緩流動引起的振動具有一定效果。

顯然柱體表面的形狀直接影響流場結構及其振動，因此探究何種參數的柱體表面可以產生更加寬泛的振動區間和更大的振動幅度是提高無葉片風力發電的關鍵。本文將波浪型圓柱和錐型圓柱相融合形成波浪錐型圓柱，探究波浪錐型圓柱的耦合振動機理，使波浪錐型圓柱具有更好的振動響應特性，為無葉片風力俘能結構渦致振動的增大和發電效率的提升提供理論支持。

1 幾何模型及數值方法

1.1 幾何模型

基于Lam等[14]的研究，本文提出將波浪型圓柱和錐型圓柱相融合形成波浪錐型圓柱，波浪錐型圓柱母線余弦波隨著高度Z的增加具有一定的斜率k，主要的幾何特征可用式(1)和式(2)描述為

(1)

Dm=(Dmax+Dmin)/2

(2)

k=(Dmax-Dmin)/2H

(3)

式中：DZ為波浪錐型圓柱在展向方向(Z坐標)上的橫截面直徑；Dmax和Dmin分別為錐型圓柱截面的最大和最小直徑；Dm為波浪錐型圓柱的平均直徑；α為余弦波浪的波幅；λ為余弦波浪的波長；k為余弦波浪的傾斜斜率；H為波浪錐型圓柱的高度，在本文中，高度為7Dm，選取展向中間位置為平均直徑Dm=0.01 m。波浪錐型圓柱每個波長內的最大直徑截面和最小直徑截面分別命名為Node和Saddle；波浪錐型圓柱的幾何參數以及流場計算域的大小進行無量綱時均采用平均直徑為單位，如圖1所示。圖1中DL和DH分別為錐型圓柱底段和頂端截面直徑。本文所計算的幾種波浪錐型圓柱參數，如表1所示。

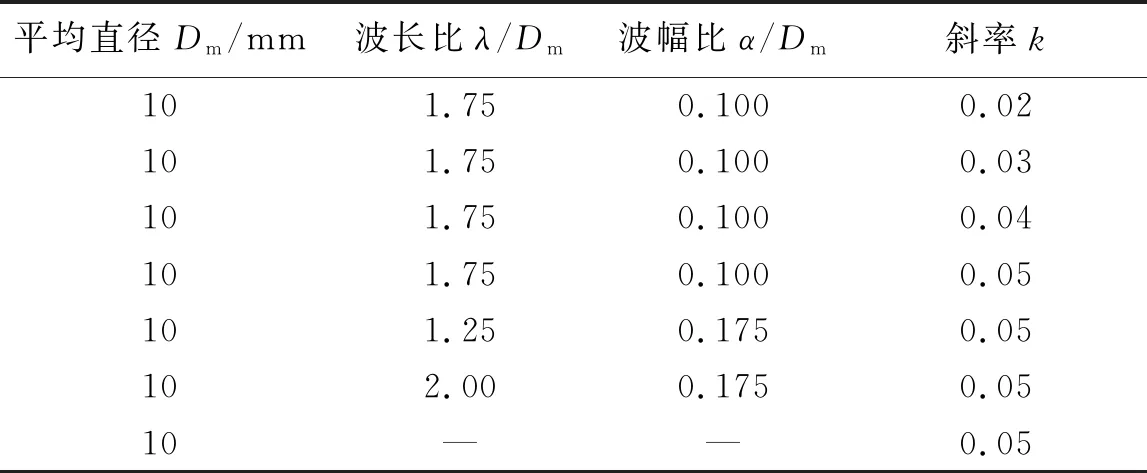
表1 波浪錐型圓柱相關參數

圖1 波浪錐型圓柱結構示意圖

1.2 數值計算方法及計算域

在渦激振動模型中，本文通過用戶自定義函數(user-defined-function，UDF)控制網格的變形與運動，將波浪錐型圓柱的渦激耦合振動簡化為彈簧阻尼系統

(4)

式中：y(t)為波浪錐型圓柱的位移，變量上的點為對時間的導數；m為波浪錐型圓柱的質量；c為系統的阻尼系數；g為系統的彈性剛度；Fy為波浪錐型圓柱受到流體施加的作用力。

在網格更新過程中首先使用Compute_Force_and_Moment宏定義獲取波浪錐型圓柱所受外力；然后再根據四階龍格-庫塔法計算出波浪錐型圓柱的位移和速度；最后將求得的橫向位移和速度用于更新網格。本文采取重疊網格的方法，因此使用DEFINE_ZONE_MOTION宏定義控制組件網格區域的整體運動。

截止到2018年12月，在裝有Android系統的手機等設備的應用界面，以“俄語”、“俄羅斯”為關鍵詞搜索相關軟件（不包括游戲），只有十幾款。那么，俄語等級測試APP的現狀就更不容樂觀了。市場上可供使用的俄語等級測試APP的現狀如下：只針對俄語等級測試的APP只有Bears這一款。俄語7500km雖然也涉及俄語等級測試的內容，但其全部內容卻包括俄語學習的方方面面，比較寬泛。而俄語研習社、俄語擺渡專八刷題寶典、俄語堂雖同樣包括俄語等級測試的內容，但皆屬于微信小程序，需要依托微信平臺（但微信小程序除需借助微信平臺外，其他大體上與APP相似，所以在這里一并進行了分析）。

在參考Lam等流場計算域的大小之后，本文將波浪錐型圓柱計算域的大小確定為30.0Dm×20.0Dm×10.0Dm，X坐標軸為順流向方向，Y坐標軸為橫流向方向，Z坐標軸為展向方向。以波浪錐型圓柱底面圓心為坐標系原點，在順流向方向上，上游入口邊界距離原點10.0Dm，下游出口邊界距離原點20.0Dm；在橫流向方向上，兩側邊界距離原點10.0Dm；在展向方向上，底部邊界距離原點為1.5Dm，如圖2所示。這樣設置即保證了流體到達波浪錐型圓柱表面時為均勻流，又避免了計算域邊界對波浪錐型圓柱周圍流場狀態的干擾。

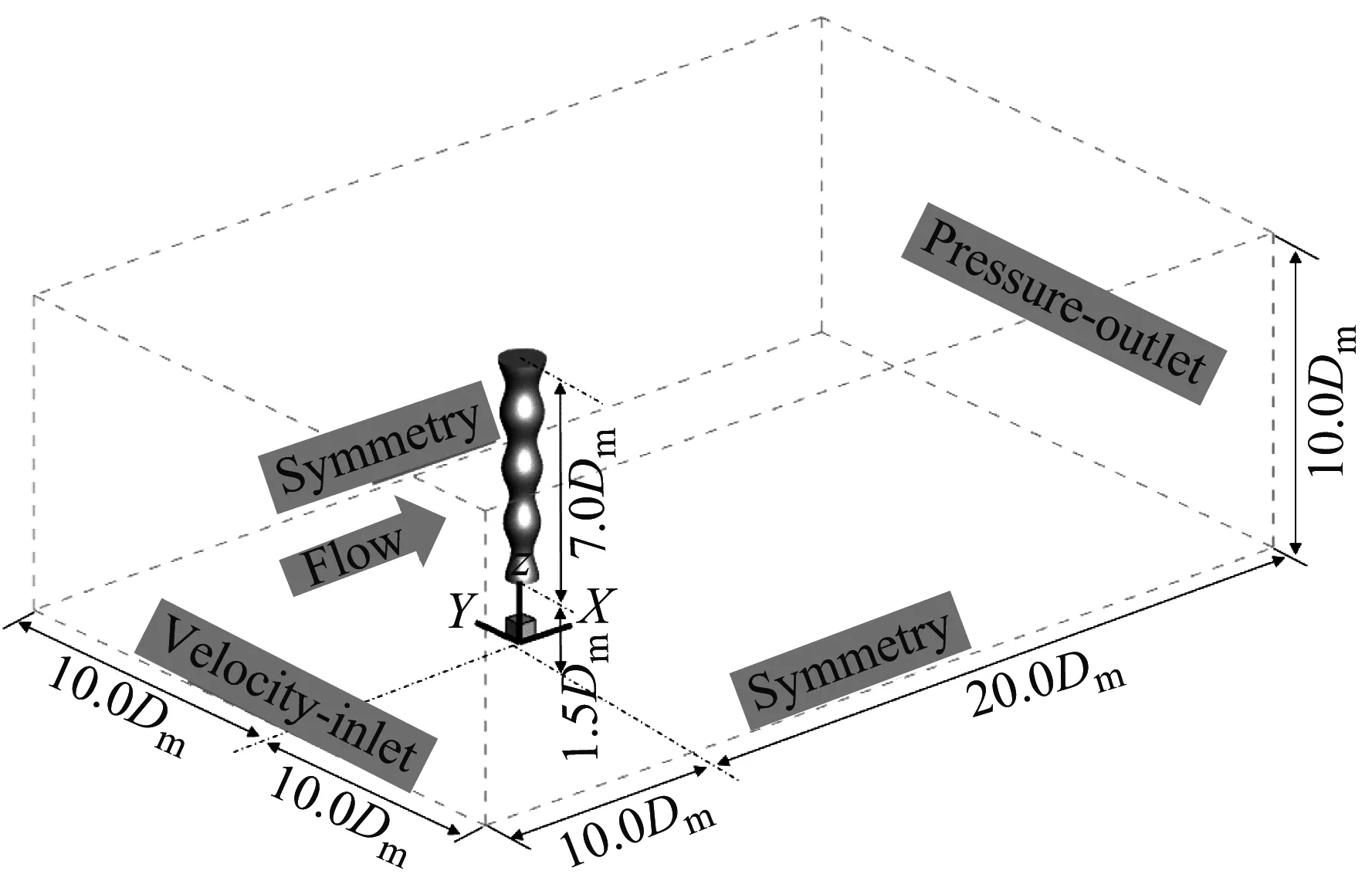
圖2 波浪錐型圓柱計算域

邊界條件設置：上游入口邊界采用均勻速度入口邊界，在Re=3 900的條件下，入口速度為5.772 m/s；下游出口邊界設置為壓力出口邊界，相對壓力為0；左右兩側、底部以及頂部邊界均設置為對稱邊界；波浪錐型圓柱表面設置為無滑移壁面。

1.3 計算模型及程序試驗驗證

取單個直圓柱進行單自由度渦激振動的數值模擬與試驗驗證，并將仿真和試驗結果與文獻作對比以驗證計算模型和UDF程序的正確性。

試驗示意圖，如圖3所示。該風洞試驗段截面尺寸為450 mm×450 mm，試驗段的前后壁面各有直徑為280 mm的可拆卸蓋板，邊界層厚度為18 mm左右。直圓柱的試驗模型根據工程實例按6∶1等比例放大，直徑為60 mm，風洞中的長度為445 mm，模型上下兩端各伸出50 mm，在延長段兩側都開有小孔方便懸掛彈簧，根據雷諾數相似準則調整進風口風速。試驗裝置如圖4所示。試驗物件采用3D打印技術，因此試驗物件的質量比m*=15.8。

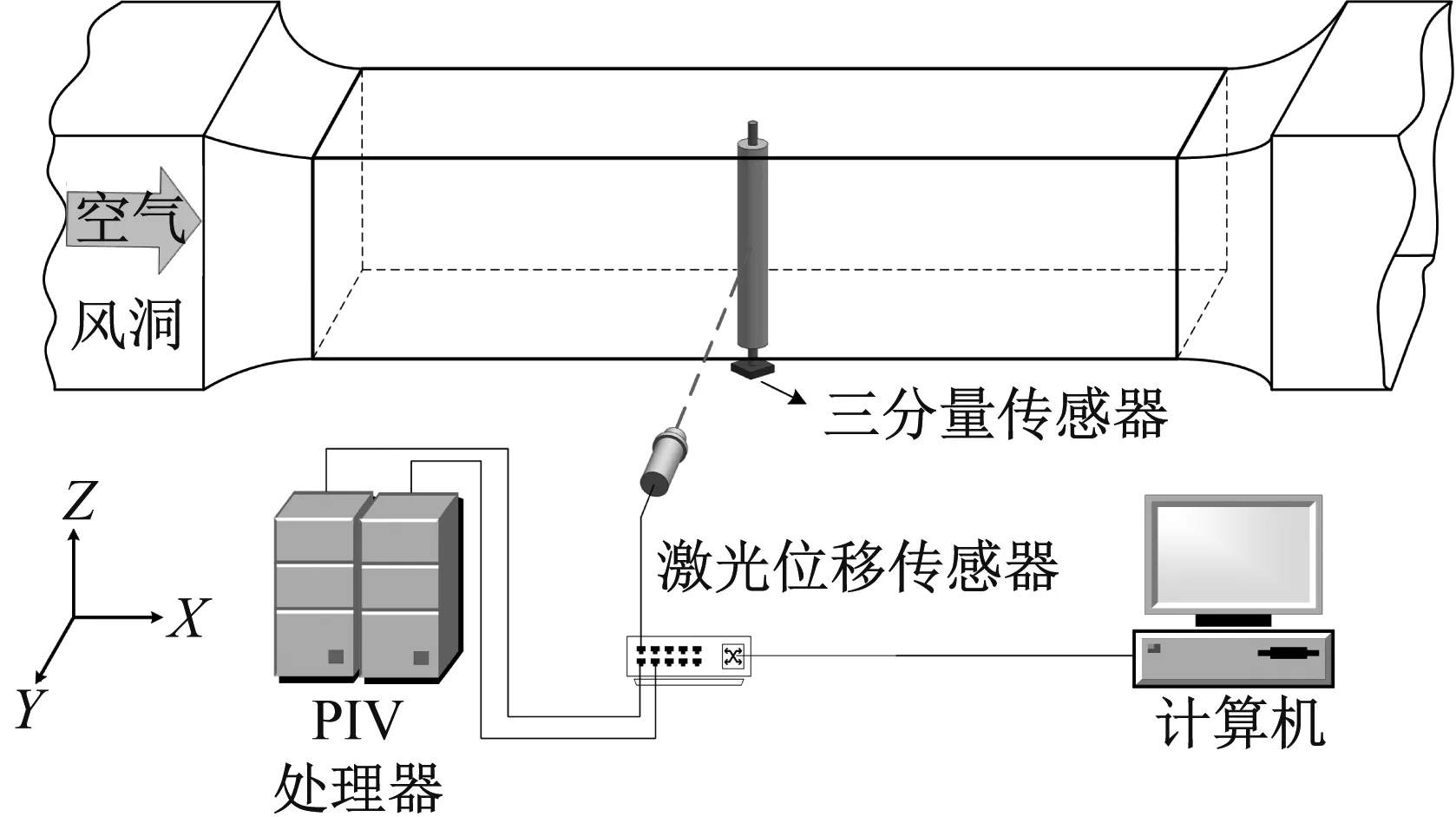
圖3 試驗示意圖

圖4 試驗裝置布置圖

單自由度圓柱最大振幅比隨折合流速Ur變化的變化曲線，如圖5所示。由圖5可知，仿真結果與汪秒[15]的研究結果非常接近。由于試驗件的質量比m*=15.8和附加質量的存在，使試驗最大振幅比比仿真結果大30.8%，但是其鎖頻區間以及整體趨勢變化一致，因此可以認為本文的計算模型和UDF程序是正確可靠的。

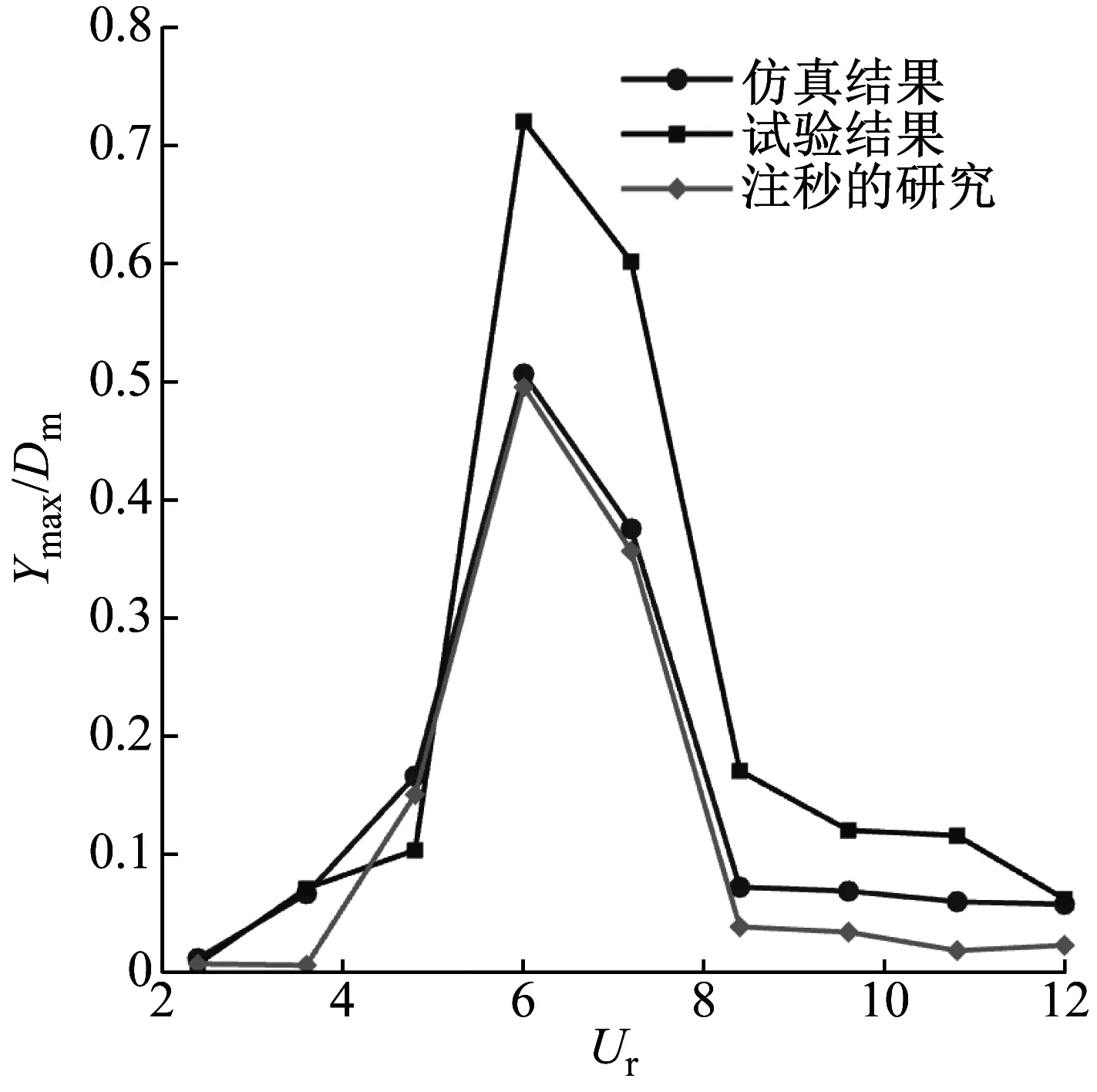
圖5 單自由度圓柱渦激振動隨折合流速Ur的變化情況

2 計算結果及分析

2.1 振動響應特性分析

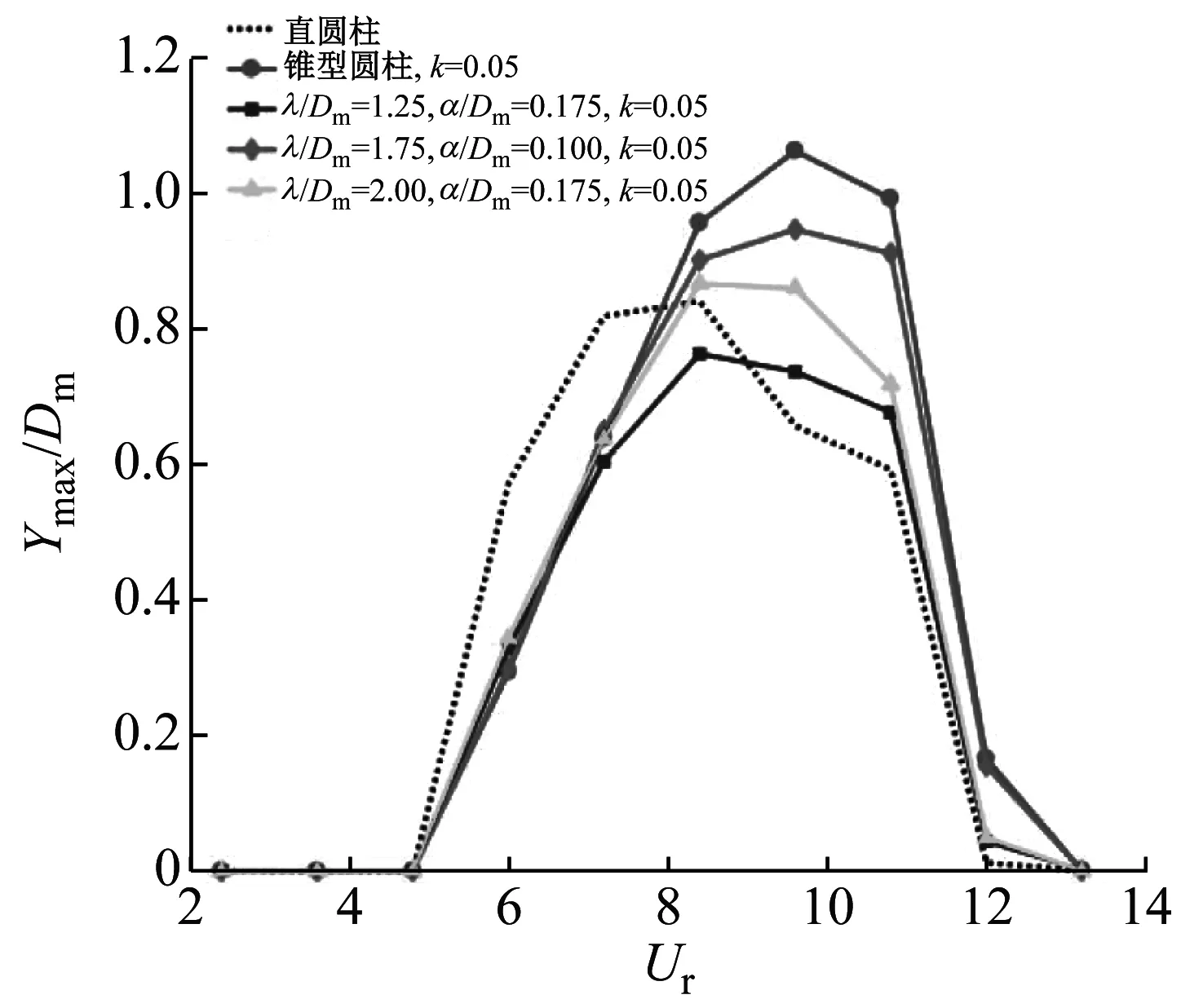
不同波長比、不同波幅比、斜率k=0.05和波長比λ/Dm=1.75、波幅比α/Dm=0.10、不同斜率的兩個系列的波浪錐型圓柱最大振幅比Ymax/Dm隨折合流速Ur的變化情況，如圖6所示。

由圖6可知：當折合流速Ur<6.0時，直圓柱的最大振幅比Ymax/Dm基本保持在0附近；當Ur=6.0時，直圓柱的最大振幅比Ymax/Dm開始急劇上升，并且在折合流速Ur=8.4時，最大振幅比達到最大值Ymax/Dm=0.841；隨后隨著折合流速的增大最大振幅比開始逐漸減小，當折合流速Ur>10.8時，最大振幅比開始急劇減小到0附近。這說明直圓柱在折合流速Ur=4.8～6.0時開始進入鎖頻區間，在折合流速Ur=10.8～12.0時開始退出鎖頻區間。對于斜率k=0.05的錐型圓柱和不同波長比、不同波幅比、斜率k=0.05的波浪錐型圓柱，當折合流速Ur<6.0時與直圓柱相似，最大振幅比維持在0附近；當6.07.2時，錐型圓柱和不同參數的波浪錐型圓柱最大振幅比開始出現區別，波幅比α/Dm=0.175、斜率k=0.05、波長比λ/Dm分別為1.25、2.00的兩個波浪錐型圓柱在折合流速Ur=8.4時分別達到最大值0.764和0.867，隨后開始緩慢降低。而波長比λ/Dm=1.75、波幅比α/Dm=0.10，斜率k=0.05的波浪錐型圓柱和斜率k=0.05的錐型圓柱最大振幅比在折合流速Ur=9.6時才達到最大值，分別為0.947和1.063。各個參數的波浪錐型圓柱和斜率k=0.05錐型圓柱在折合流速Ur>10.8時，最大振幅比快速減小，退出鎖頻區間。

(a)

由圖6(b)可知：波長比λ/Dm=1.75、波幅比α/Dm=0.10、不同斜率的波浪錐型圓柱最大振幅比隨著折合流速Ur的增長變化趨勢與直圓柱的變化趨勢相似，在折合流速Ur=4.8～6.0時進入鎖頻區間，在折合流速Ur=10.8～12.0時退出鎖頻區間。但是波長比λ/Dm=1.75、波幅比α/Dm=0.10，斜率k=0.05的波浪錐型圓柱在折合流速Ur=9.6時，最大振幅比達到最大值，而其他斜率的波浪錐型圓柱最大振幅比均在折合流速Ur=8.4時達到最大值；斜率k=0.02、0.03和0.05的波浪錐型圓柱最大振幅比的最大值均在0.95附近出現，而斜率k=0.04的波浪錐型圓柱最大振幅比的最大值為0.872。

綜合圖6(a)和圖6(b)可知：不同參數的波浪錐型圓柱和直圓柱以及斜率k=0.05的錐型圓柱相比，最大振幅比各不相同。直圓柱的最大振幅比在折合流速Ur=8.4時達到最大值0.841，波長比λ/Dm=1.75、波幅比α/Dm=0.10，斜率k=0.05的波浪錐型圓柱最大振幅比的最大值與直圓柱相比增大12.6%，斜率k=0.05的錐型圓柱與直圓柱相比增大26.4%。這意味著柱體表面的變化對渦激振動的鎖頻區間基本沒有影響，但是對最大振動幅度有影響。

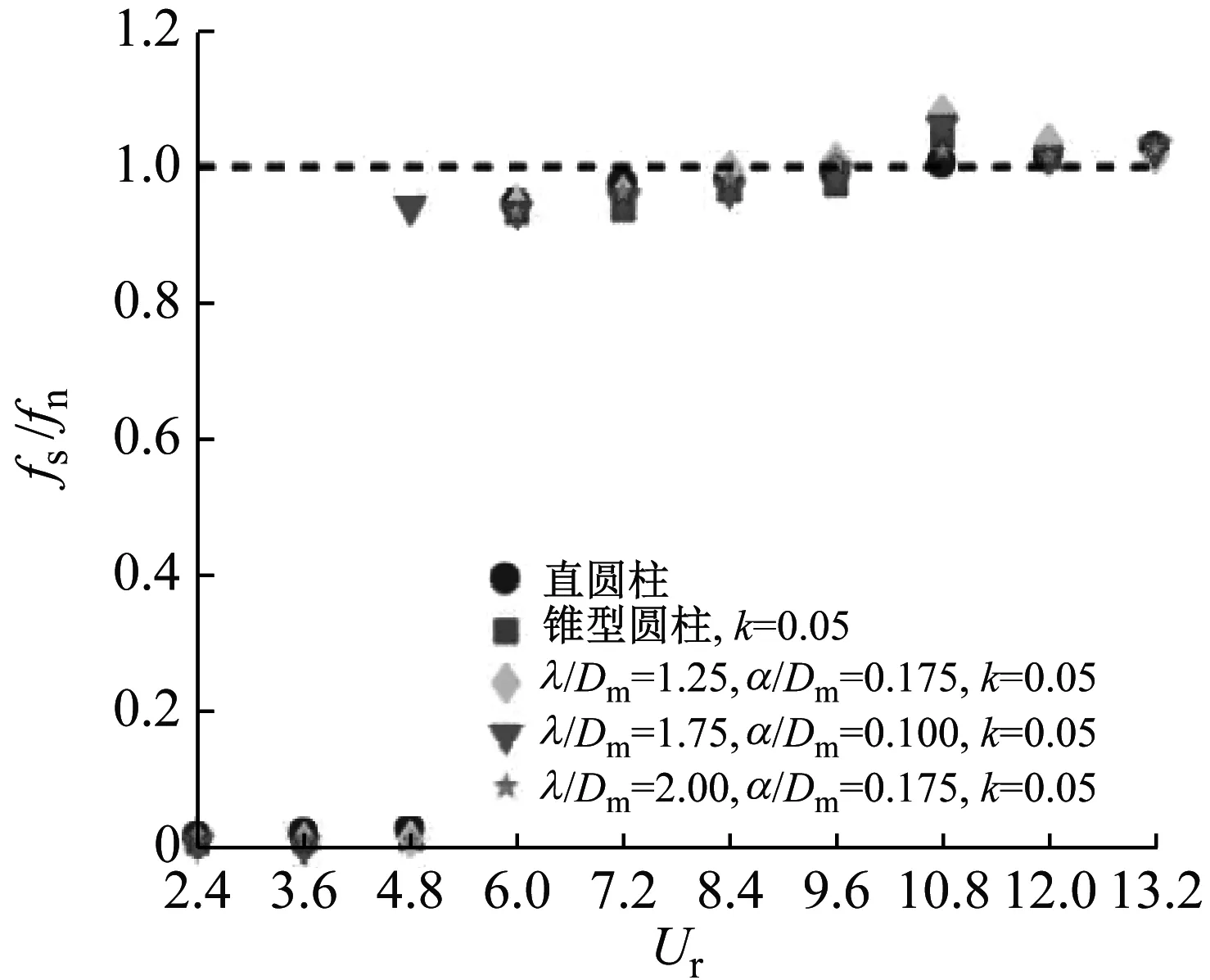
為了更好分析不同參數的振動響應特性，接下來將分析直圓柱、斜率k=0.05的錐型圓柱以及不同參數的波浪錐型圓柱的頻率比隨著折合流速Ur變化的變化情況，如圖7所示。圖7中：fs為渦脫頻率；fn為系統固有頻率。

(a)

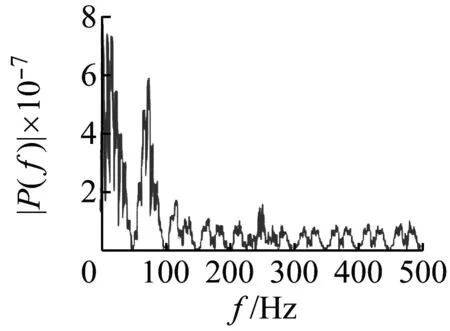
由圖7可知：當折合流速Ur<6.0時，直圓柱、斜率k=0.05的錐型圓柱和各個參數的波浪錐型圓柱其尾流瀉渦頻率比基本為0；當折合流Ur≥6.0時，尾流瀉渦頻率比迅速增加到0.93左右，隨著折合流速Ur的增大，尾流瀉渦頻率比緩慢增加，基本維持在1附近，即fs=fn。雖然隨著折合流速Ur的增加，尾流瀉渦頻率比并沒有遠離1，而是保持在fs=fn附近；但由圖6可知，當折合流速Ur>12.0時，波浪錐型圓柱渦激振動已經退出鎖頻區間，為此，選取波長比λ/Dm=1.75、波幅比α/Dm=0.10、斜率k=0.05的波浪錐型圓柱為研究對象，分析其尾流瀉渦頻譜圖，如圖8所示。圖8中橫軸為頻率，縱軸P(f)為功率譜密度。由圖8可知：當6.0≤Ur≤10.8時，尾流瀉渦頻譜的幅值均大于0.04；當折合流速Ur>10.8時，頻率的幅值由0.05迅速降低到1×10-4以下，這說明雖然此時尾流瀉渦頻率與固有頻率接近，但是能量很小，不能使波浪錐型圓柱產生共振，從而使波浪錐型圓柱渦激振動迅速退出鎖頻區間。

(a) Ur=2.4

2.2 升阻力系數分析

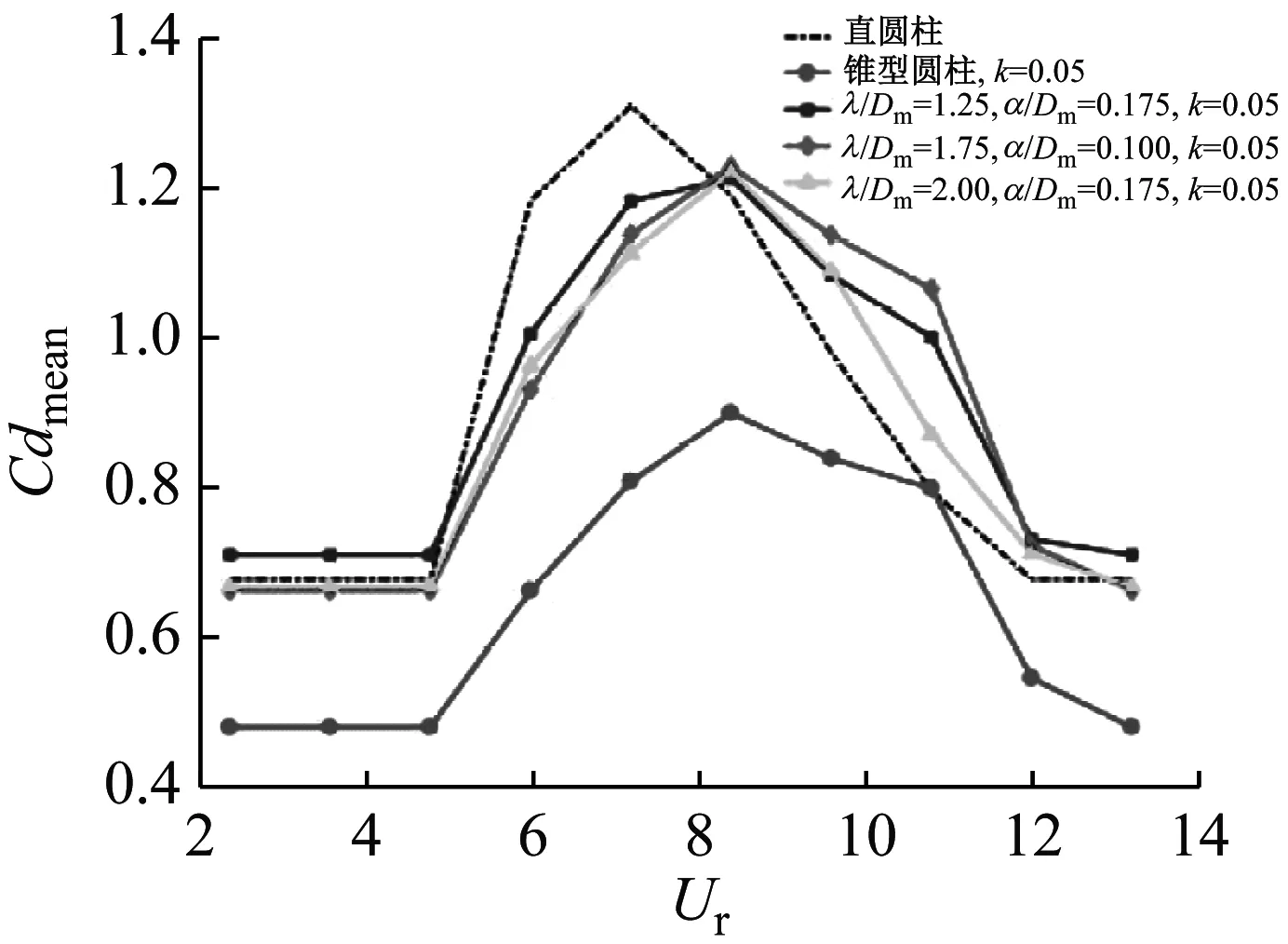
波浪錐型圓柱平均阻力系數隨著折合流速增加的變化情況，如圖9所示。為了更好的探究波浪錐型圓柱不同參數所產生的影響，分別加入了直圓柱和斜率k=0.05的錐型圓柱作比較。由圖9(a)可知：當折合流速Ur<6.0時，折合流速對平均阻力系數基本沒有影響，直圓柱和各個參數的波浪錐型圓柱平均阻力系數均保持在0.678附近，而斜率k=0.05的錐型圓柱平均阻力系數卻保持在0.481左右，與直圓柱相比降低29.05%；當折合流速Ur=6.0時，直圓柱、錐型圓柱和各個參數的波浪錐型圓柱的平均阻力系數均開始急劇上升，這意味著開始進入鎖頻區間，直圓柱、錐型圓柱和各個參數的波浪錐型圓柱的最大振幅比也開始快速增大(見圖6)；隨著折合流速的增大，直圓柱在折合流速Ur=7.2時，平均阻力系數達到最大值，而錐型圓柱和波浪錐型圓柱的平均阻力系數在折合流速Ur=8.4時達到最大值，然后隨著折合流速的增加開始緩慢下降；當折合流速Ur≥12.0時，平均阻力系數維持在一個穩定的值。而圖9(b)表示波長比λ/Dm=1.75、波幅比α/Dm=0.10、不同斜率k的波浪錐型圓柱的平均阻力系數。可以看出平均阻力系數的變化趨勢與圖9(a)相似，只是平均阻力系數最大值各不相同。

(a)

波浪錐型圓柱脈動升力系數隨折合流速增加的變化情況，如圖10所示。當折合流速Ur<6.0時，直圓柱、斜率k=0.05的錐型圓柱以及各個參數波浪錐型圓柱的脈動升力系數均為0，此時最大振幅比也基本為0，柱體并沒有進入鎖頻區間。當折合流速Ur≥6.0時，脈動升力系數出現跳躍急劇增加的現象，最大振幅比在相同的折合流速下也出現跳躍，從0開始迅速增大，這意味著直圓柱、斜率k=0.05的錐型圓柱和各個參數波浪錐型圓柱開始進入鎖頻區間。當折合流速Ur=6.0～9.6時，脈動升力系數隨著折合流速的增加迅速降低至0.1附近。當折合流速Ur>9.6時，隨著折合流速的增加脈動升力系數緩慢減小并趨于穩定。直圓柱、斜率k=0.05的錐型圓柱以及各個參數波浪錐型圓柱的脈動升力系數在不同折合流速下的最大值，如表2所示。直圓柱和波長比λ/Dm=1.75、波幅比α/Dm=0.10、斜率k=0.02波浪錐型圓柱脈動升力系數的最大值分別達到0.688和0.768。斜率k=0.05的錐型圓柱和其他參數波浪錐型圓柱的脈動升力系數的最大值介于0.40～0.52，這可能是因為最大振幅比不僅僅與脈動升力系數有關，還和平均阻力系數、波浪錐型圓柱表面形狀等參數密切相關，是綜合相互影響的結果。

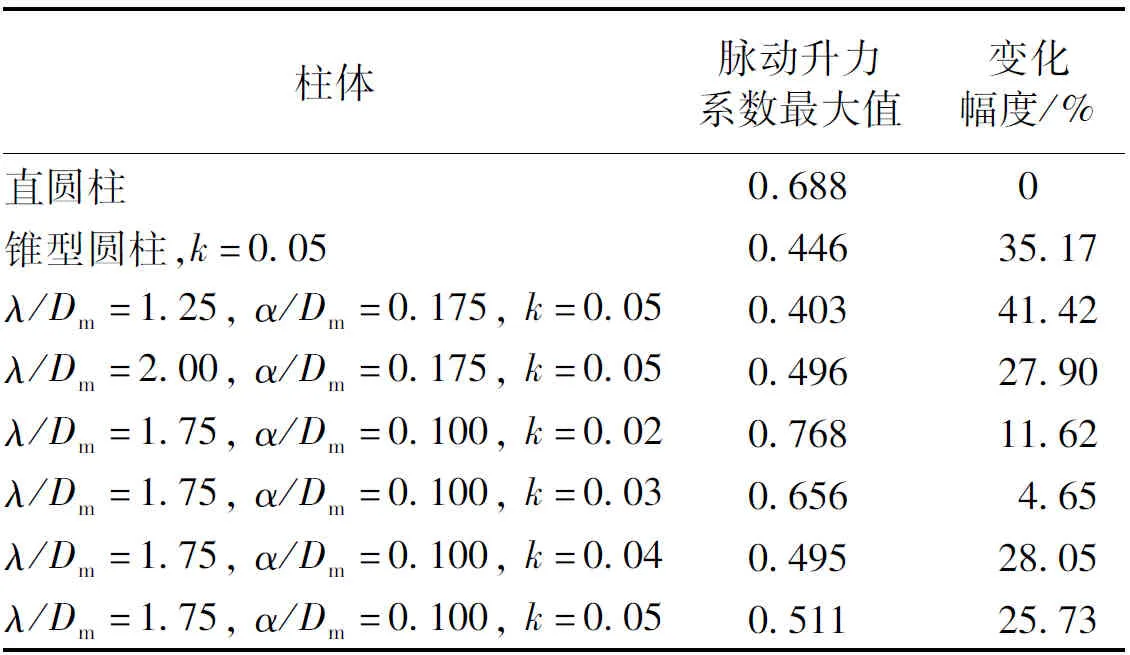
表2 脈動升力系數最大值變化情況

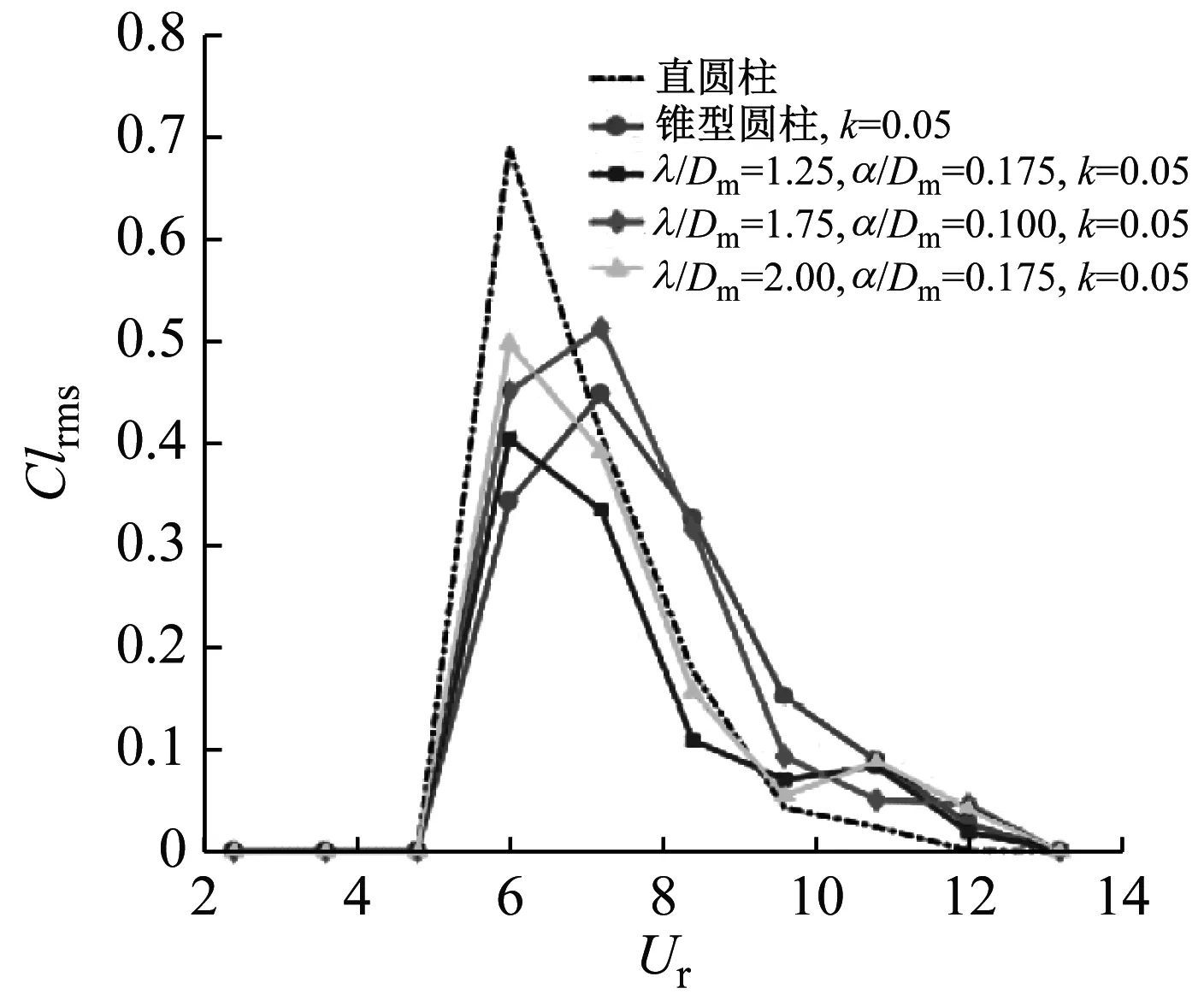
(a)

2.3 相位轉化以及流場分析

斜率k=0.05的錐型圓柱和波長比λ/Dm=1.75、波幅比α/Dm=0.10、斜率k=0.05的波浪錐型圓柱在折合流速6.0～12.0的條件下，升力系數與位移的時程圖，如圖11、圖12所示。由圖11、圖12可知：當折合流速Ur=6.0、7.2和8.4時，錐型圓柱和波浪錐型圓柱的升力系數Cl和振動位移Y/Dm都呈現出“同相位”的特征，且隨著折合流速的增大，振動位移不斷增大，渦激振動處于鎖頻區間的開始位置；當折合流速Ur=9.6時，錐型圓柱和波浪錐型圓柱的升力系數與位移的時程圖與折合流速Ur<9.6時一樣，呈現出“同相位”的特征，但是除此之外，升力系數還呈現出“拍”的特征；當折合流速Ur=10.8時，錐型圓柱的升力系數與位移呈現出“同相位”的特征，同時也呈現出“拍”的特征，結合錐型圓柱的最大振幅比的變化圖(見圖6)可以得出，這是造成錐型圓柱在鎖頻區間內最大振幅比一直保持很大振幅的原因，而此時波浪錐型圓柱的升力系數與位移時程圖的特征與錐型圓柱卻不同，波浪錐型圓柱的升力系數與位移出現“同相位”與“反相位”交替出現的特征，即在一個周期內出現兩個峰值；當折合流速Ur=12.0時，錐型圓柱和波浪錐型圓柱的升力系數和位移均呈現出“反相位”特征，此時渦激振動開始退出鎖頻區間，振動位移也開始減小。

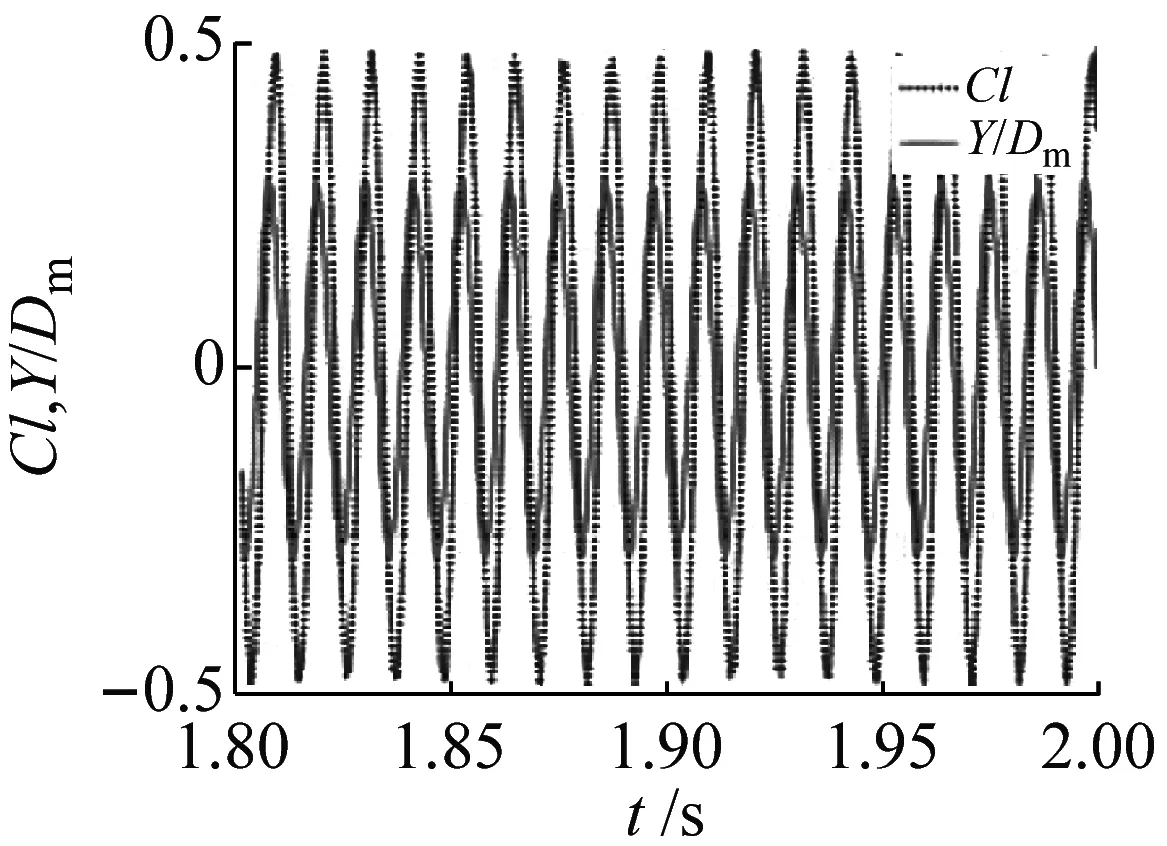
(a) Ur=6.0

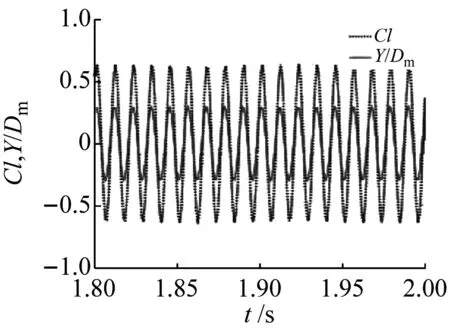
(a) Ur=6.0

由于當波浪錐型圓柱進行渦激振動時，折合流速對柱體的流動結構以及渦脫狀態影響非常大，從圖6可知，波浪錐型圓柱在鎖頻區間內和在鎖頻區間外的受力和位移差別是非常大的，而柱體的振動位移又影響著流場的結構。因此本節根據圖6的研究結果，選取斜率k=0.05的錐型圓柱和波長比λ/Dm=1.75、波幅比α/Dm=0.10、斜率k=0.05的波浪錐型圓柱為對象，詳細分析在不同折合流速內流場的分布情況，在展向方面中間Z截面(Z=0.5H)的渦量圖，如圖13、圖14所示。

由圖13、圖14可知，當折合流速Ur<6.0時，錐型圓柱和波浪錐型圓柱尾流出現兩個很長的剪切層，沒有明顯渦脫產生。結合圖6、圖10的結果分析，此時錐型圓柱和波浪錐型圓柱的最大振幅比、脈動升力系數都基本為0，可以得出這種流動結構使柱體保持穩定狀態。當6.0≤Ur≤8.4時，錐型圓柱和波浪錐型圓柱脈動升力系數和最大振幅比迅速增大，尾流出現“2S”模式渦脫，即兩個大小相同、方向相反的渦交錯脫落。當折合流速Ur=9.6和10.8時，錐型圓柱尾流渦脫出現“2P”模式，即兩個渦的能量大小不相等、旋轉方向相反；并且隨著渦脫向下游發展，顯現出“2C”模式的跡象，即柱體兩側各出現一對旋轉方向相同的渦，但是柱體兩側渦對的旋轉方向相反。這意味此時錐型圓柱的渦脫模式有可能實現由“2P”到“2C”的模式轉變。此時對于波浪錐型圓柱，渦脫模式依舊是“2S”模式，但是和6.0≤Ur≤8.4時波浪錐型圓柱的渦脫相比，尾流的脫落渦的長度更長。當折合流速Ur=12.0時，錐型圓柱的渦脫又重新出現“2S”模式，但是渦脫的長度與之前相比更長更扁，向著層流的方向發展。當折合流速Ur=13.2時，錐型圓柱和波浪錐型圓柱的流動結構與折合流速Ur<6.0時一致，尾流出現兩個很長的剪切層，流動狀態重新趨于穩定，此時錐型圓柱和波浪錐型圓柱退出鎖頻區間，最大振幅比和脈動升力系數急劇減小至0附近。

(a) Ur=2.4

3 結 論

本文選取了兩個系列的波浪錐型圓柱，分別是波長比λ/Dm=1.75、波幅比α/Dm=0.10、不同斜率(k=0.02、0.03、0.04和0.05)的波浪錐型圓柱和斜率k=0.05、不同波長比(λ/Dm=1.25、1.75和2.00)、不同波幅比(α/Dm=0.10和0.175)的波浪錐型圓柱，加入直圓柱和斜率k=0.05的錐型圓柱作對比，探究不同折合流速(Ur=2.4～13.2)對各個波浪錐型圓柱渦激振動響應特性的影響，分析波浪錐型圓柱的振動響應特性、升阻力特性以及流動結構，主要得出以下結論：

(1) 直圓柱和錐型圓柱以及各個參數的波浪錐型圓柱的鎖頻區間基本一致，但是各個參數的波浪錐型圓柱最大振幅比各不相同，其中斜率k=0.05的錐型圓柱和波長比λ/Dm=1.75、波幅比α/Dm=0.10、斜率k=0.05的波浪錐型圓柱最大振幅比較大，不同折合流速下其最大振幅比的最大值和直圓柱相比分別增長26.4%和12.6%。

(2) 在鎖頻區間內(4.8