基于能量一致積分的拉索-阻尼器實時混合試驗方法

楊 格， 孫紅碩， 吳 斌， 潘天林， 王 貞

(1.武漢理工大學 土木工程與建筑學院，武漢 430070;2.天津大學 中國地震局地震工程綜合模擬與城鄉抗震韌性重點實驗室，天津 300350；3.東北電力大學 建筑工程學院，吉林 132012)

斜拉索因其結構柔、質量輕，在風荷載等外力作用下非常容易發生振動。由于拉索振動易導致拉索錨固端發生疲勞破壞等問題，需要采取措施來抑制其大幅度振動，工程中廣泛采用的措施是在拉索錨固位置附近安裝阻尼器。為了研究阻尼器對拉索的減振效果，一般采用數值模擬[1]或室內試驗[2]的方式來獲取拉索-阻尼器系統的動力響應。數值模擬應用方便，但現有的阻尼器數值模型均存在一定的簡化，不能真實反應阻尼器在實際結構中的性能。室內試驗因試驗場地規模和技術等問題，很難對較長拉索進行真實工況下的模擬。

結構混合試驗方法可以將結構中無法準確模擬的部分作為試驗子結構，其他部分采用數值模型，兩者在線交互完成對整體結構的模擬。該方法解決了因實驗室場地規模限制等因素而無法開展大型結構試驗的問題，被廣泛應用于結構抗震試驗研究中[3-6]。其中，實時混合試驗方法能夠考慮加載速度的影響，可實現對速度相關型試件力學性能的準確反映。鑒于實時混合試驗的這一優點，可以將拉索作為數值子結構，阻尼器作為試驗子結構，開展拉索-阻尼器系統的實時混合試驗。該方法對研究拉索-阻尼器系統中阻尼器的減振效果有著重要意義。

實時混合試驗對數值模型的計算效率有著極高的要求。為了保證計算效率，現有關于拉索-阻尼器實時混合試驗的研究大多采用簡化的數值模型來模擬拉索。Jung等[7]對拉索-阻尼器系統在不同風速下的響應進行了實時混合試驗，其拉索數值模型采用伽遼金方法得到。伽遼金方法是一種簡化計算方法，其在拋物線假設的基礎上引入一個參數來考慮索垂度以減少計算量；而傳統有限元分析是通過自重作用下索的形狀來得到垂度，因此伽遼金方法計算精度要比傳統有限元分析計算精度差。Duan等[8]建立了基于向量式有限元的拉索模型，阻尼器采用線性黏滯阻尼器數值模型來代替，對拉索-阻尼器系統的一階模態振動進行了實時混合試驗數值仿真。相對于傳統有限元方法，基于向量式有限元的拉索模型具有更高的計算效率，但其在進行質點運動方程求解時，采用了顯式的中心差分法。中心差分法是一種對線性體系有條件穩定的算法，而拉索-阻尼器系統屬于強非線性系統，一方面拉索振動具有較強的幾何非線性;另一方面阻尼器也往往具有很強的非線性，因此無法保證中心差分法在拉索-阻尼器系統動力分析中的穩定性。當拉索存在高頻振動時，通常需要很小的時間步長來滿足算法的計算精度和穩定性要求[9]，仍然存在計算時間可能超過時間步長而導致試驗失敗的問題。

因此，在拉索-阻尼器系統的實時混合試驗中需要對非線性體系無條件穩定的時間積分方法。然而，目前混合試驗中常用的無條件穩定時間積分方法主要是針對線性體系，如無條件穩定的顯式CR方法(Chen and Ricles)[10-12]、顯式Chang方法族[13]、隱式平均加速度法[14]、隱式中點法[15]等。對于非線性體系，Crisfield等[16]采用平均加速度法求解桁架單元的動力方程時，發現結果會出現發散。潘天林[17]通過對具有幾何非線性的桁架體系進行分析，發現隱式平均加速法和隱式中點方法不能保證無條件穩定。Kuhl等[18]發現基于桁架單元的能量耗散積分方法也會存在計算結果不穩定的現象。為了實現對非線性體系的無條件穩定，Wu等[19]提出了能量一致積分方法，并將基于梁柱單元的能量一致積分方法應用到足尺鋼框架結構的混合試驗中。由于能量一致積分方法為隱式算法需要迭代，目前該積分方法方法尚未應用于實時混合試驗中。考慮到近年來混合試驗為應對速度相關型試件的精細化模擬需求，逐漸趨于有限元化和實時化[20]，因此，將能量一致積分方法應用于實時混合試驗中具有重要意義。

能量一致積分方法是一種隱式方法，將其應用于實時混合試驗時，會遇到迭代導致作動器加載速度波動較大的問題。對于阻尼器試件，加載速度波動較大會導致測得的阻尼器出力嚴重失真，致使試驗失敗。為此，本文提出了基于能量一致積分的拉索-阻尼器系統實時混合試驗方法，一方面通過Jung等[21]提出的固定迭代次數并對迭代位移進行插值的方式來求解隱式差分方程，實現平滑加載；另一方面為保證試驗過程中拉索-阻尼器系統的能量一致，對試驗測得的阻尼器出力進行恢復力修正。在不考慮拉索抗彎剛度的情況下，拉索可由若干個桁架單元模擬，本文將基于桁架單元的能量一致積分方法應用于拉索-阻尼器系統的實時混合試驗中，對拉索-阻尼器系統進行了一階模態振動下的實時混合試驗數值仿真，驗證了方法的可行性。

1 基于桁架單元的能量一致積分方法基本原理

對于桁架單元，連續的動力方程可以表示為

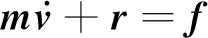
(1)

式中,m、v、r和f分別為質量矩陣、速度向量、節點力向量和外荷載向量。其中節點力向量r可表示為

r=N[-ee1]T

(2)

式中:N為單元的軸力;e1為桁架單元的軸向單位向量

(3)

式中:x=xQ-xP為節點坐標差，xP與xQ分別為桁架兩個節點的坐標向量;L為單元的長度。

桁架單元的節點力考慮了幾何非線性和材料非線性的影響，其中幾何非線性由向量e1考慮，材料非線性則由N考慮。為了實現單元的能量一致，需要對恢復力進行非線性修正，其修正格式為

(4)

ri+β=r[(1-β)ui+βui+1]，

ri+1-β=r[βui+(1-β)ui+1]

(5)

式中：β為修正系數；ui、ui+1分別為第i、第i+1個積分點時刻的位移向量。然后分別對式(2)中兩項非線性相關向量進行離散，對e1離散得到

(6)

式中,β1為幾何非線性修正系數。對N離散得到

(7)

式中,β2為材料非線性修正系數。能量一致積分方法采用平均加速度法對位移和速度的假設

(8)

(9)

式中：Δt為時間積分步長；vi、vi+1分別為第i、i+1個積分點時刻速度向量；ai、ai+1分別為第i、第i+1個積分點時刻加速度向量。

基于此，式(1)的離散形式可表示為

(10)

式中:fi、fi+1分別為第i、第i+1個積分點時刻外荷載向量;εi、εi+1分別為第i、第i+1個積分點時刻的應變;A0為桁架單元原截面面積;L0為桁架單元原長;σ為工程應力;第三式和第四式分別為關于β1和β2的非線性方程。由于能量一致積分方法為隱式算法，整體節點力方程的求解通過牛頓迭代實現。

2 基于能量一致積分的拉索-阻尼器實時混合試驗方法

2.1 基于能量一致積分的拉索-阻尼器實時混合試驗方法基本原理

在拉索-阻尼器系統的實時混合試驗中，以拉索作為數值子結構，阻尼器作為試驗子結構，連續的動力方程可以表示為

(11)

式中:rN為數值子結構恢復力向量；rE為試驗子結構恢復力向量，即阻尼器的出力。采用基于桁架單元的能量一致積分方法，式(11)可以離散為

(12)

式中:nN為桁架單元數目;βN1、βN2分別為幾何非線性修正系數和材料非線性性系數。本文假定拉索材料為線彈性，故第四式中所有桁架單元的材料非線性修正系數βN2=0。由于測得的試驗子結構恢復力rE不是連續的，故修正后的等效恢復力rEβ沒有理論解，需根據試驗數據結合第五式計算。

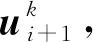
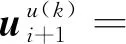
(13)

(14)

式中:k=0，1，…，n-1,n為每一積分步固定迭代次數,n=Δt/δt，Δt為積分步長，δt為采樣步長；系數m=(k+1)/n；v0、u0分別為初始速度向量和初始位移向量。在計算第一個積分步時，因為沒有上一積分點時刻的位移，位移命令可通過式(14)獲得。

在純時滯與總時滯相比非常小的情況下，作動器系統的動力性能可用不包含純時滯環節的二階傳遞函數來代替，傳遞函數可寫為

(15)

式中：s為Laplace變量；ξ為作動器系統的阻尼比；ω為作動器系統的頻率。時滯會影響實時混合試驗仿真精度[22]，但在阻尼器作為試驗子結構的實時混合試驗中，時滯對仿真精度影響一般較小，故本文不進行作動器的時滯補償。

基于能量一致積分的拉索-阻尼器系統實時混合試驗實施過程,如圖1所示。第i+1個積分步的第k次迭代實施過程可簡述為：

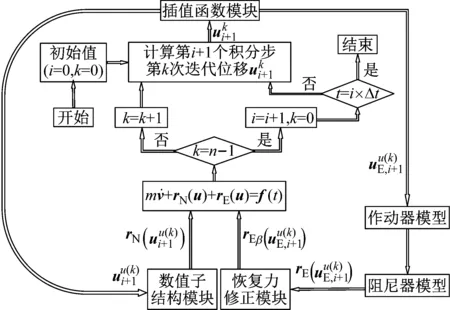
圖1 拉索-阻尼器系統實時混合試驗實施過程示意

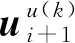
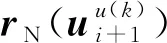
重復上述步驟，直至達到預定的固定迭代次數n，完成第i+1個積分步的模擬，并依此實現0～t時間內的仿真。

2.2 恢復力修正模塊計算方法

為保證與系統能量一致，需要通過恢復力修正模塊對測得的試驗子結構恢復力進行修正，計算等效恢復力rEβ。在拉索-阻尼器系統中，第i+1個積分步中前j次迭代阻尼器出力所做的實際總功為

(16)

(17)

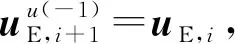
(18)

通過式(18)可以看出，分子是第i+1個積分步中前j次迭代的阻尼器出力所做總功的近似值，分母是第i+1個積分步中前j次迭代的總位移增量。通過式(18)對測得的阻尼器出力進行修正獲得等效恢復力，實現整個過程系統能量一致。

3 拉索-阻尼器系統實時混合模擬

3.1 模型的建立

表1 J26號拉索結構參數

圖2 拉索-阻尼器系統模型示意圖

3.2 拉索模型的幾何非線性和正確性驗證

對拉索模型跨中處施加一個周期的正弦位移，幅值取1 m。通過靜力分析可得拉索跨中節點恢復力-位移曲線如圖3所示。可以看出節點恢復力與位移并非呈線性關系，驗證了拉索模型的幾何非線性。

圖3 拉索跨中節點恢復力-位移曲線

記錄模擬得到的拉索1/4跨處位移時程，最大振動幅值約為2.5 mm。通過圖3可以看出，在小位移下拉索模型的恢復力-位移曲線基本處于線性階段，此時可忽略幾何非線性的影響。隨后對該位移時程進行快速傅里葉變換，可得拉索前三階模態頻率如圖4所示。與Duan等的研究中基于ANSYS軟件分析得到的拉索前3階模態頻率對比，可看出兩者所得前3階模態頻率基本一致，驗證了本文拉索模型的正確性,如表2所示。

圖4 位移功率譜密度函數

表2 拉索模態頻率對比

3.3 實時混合試驗的數值仿真

本文假定作動器系統頻率和阻尼比分別為ω=3.14 rad/s、ξ=0.8[24],以式(15)所示傳遞函數來模擬實際作動器系統。在積分步長Δt=0.05 s下，取固定迭代次數n=15，對拉索-阻尼器系統進行實時混合試驗數值仿真。為了盡可能真實地再現實際試驗的情況，阻尼器出力采用迭代點時刻的實際速度來計算，在第i+1個積分步第k個迭代點時刻速度為

(19)

(20)

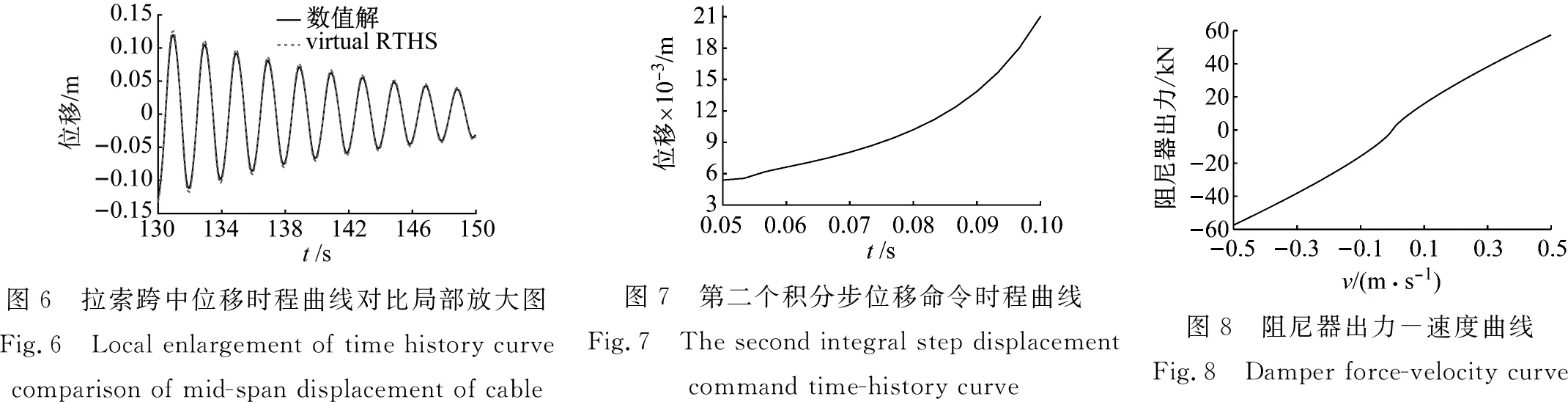
將頻率為拉索第1階模態頻率的正弦荷載300×sin(2π×0.5t)N施加于拉索的23個結點上，荷載方向均垂直于拉索，激勵100 s后釋放荷載。在阻尼器作用下，振動自由衰減，可獲得前150 s的拉索跨中位移時程，其仿真結果如圖5和圖6所示。從圖5、圖6可以看出，本文所提實時混合試驗方法的仿真結果與整體模擬的數值解吻合較好。計算得到拉索跨中位移的均方根誤差為1.96%，滿足精度要求。

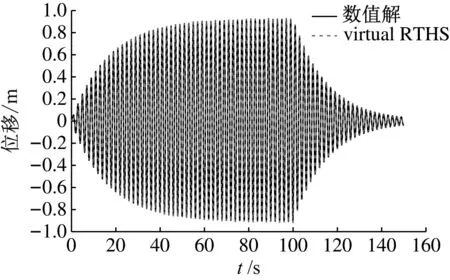
圖5 拉索跨中位移時程曲線對比(1階模態)

通過圖6可以看出，本文方法計算幅值比數值解偏大。因此，本文方法的計算結果偏于保守，有利于保證結構的安全性。

在計算效率方面，該實時混合試驗數值仿真時長為150 s，計算總耗時為9.45 s，每一積分步平均計算耗時0.003 15 s。可以看出本文所提方法計算效率較高，滿足實時要求。其中，MATLAB軟件版本為MATLAB2017b，計算機配置如表3所示。

表3 計算機配置

為了觀察基于能量一致積分的拉索-阻尼器系統實時混合試驗方法的迭代效果，取第二個積分步發給作動器模型的位移命令，如圖7所示。可以看出發給作動器的位移命令時程曲線較光滑，因此本文所提方法可保證對阻尼器試件的平滑加載。

該仿真中阻尼器出力與速度關系曲線如圖8所示。阻尼器出力與速度關系曲線滿足本文阻尼器力學模型。

4 結 論

本文提出了基于能量一致積分的實時混合試驗方法，并應用于拉索-阻尼器系統的實時混合試驗仿真中，主要結論如下：

(1) 基于桁架單元的能量一致積分方法可考慮拉索的幾何非線性，實現對拉索-阻尼器系統的振動過程數值模擬。

(2) 基于能量一致積分的實時混合試驗方法可以實現速度相關型試件的光滑加載，可應用于拉索-阻尼器系統的實時混合試驗中。